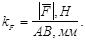что такое гладкая поверхность
Гладкая поверхность
Последняя бука буква «ь»
Ответ на вопрос «Гладкая поверхность «, 9 (девять) букв:
плоскость
Альтернативные вопросы в кроссвордах для слова плоскость
Определение слова плоскость в словарях
Энциклопедический словарь, 1998 г. Значение слова в словаре Энциклопедический словарь, 1998 г.
простейшая поверхность. Понятие плоскость (подобно точке и прямой) принадлежит к числу основных понятий геометрии. Плоскость обладает тем свойством, что любая прямая, соединяющая две ее точки, целиком принадлежит ей.
Примеры употребления слова плоскость в литературе.
Если типы и есть, то они существуют не в той плоскости, как это намечается Аарне, а в плоскости структурных особенностей сходных сказок, но об этом после.
В системе не было планет как таковых, однако еще четыре факельщика условного противника обнаружили в засаде в аккреционном диске в плоскости эклиптики.
Говорят, что в последние годы, благодаря успехам отечественной, а может быть, зарубежной химии, для летчиков изобрели что-то такое, что можно лить только на плоскости, но в то отсталое время антиобледенителем был чистый спирт-ректификат.
К району заправки шли сквозь облачность, самолет дважды пересекал зоны обледенения, дважды Тасманов по команде Боровского включал антиобледенители, освобождая от наледи плоскости крыльев и заборники двигателей.
Таким образом, Кант подчеркивает априорность категорий времени и пространства в двух плоскостях: при объяснении опыта и при объяснении науки.
Источник: библиотека Максима Мошкова
Гладкая поверхность (плоскость)
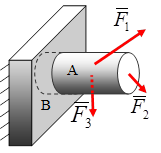
Основные понятия и аксиомы статики
Основные понятия
Статикой называется раздел теоретической механики, в котором излагается общее учение о силах и изучается равновесие материальных тел, находящихся под действием сил.
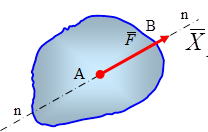
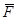
Для изображения вектора силы на чертеже в масштабе используют масштабный коэффициент
Под равновесием понимают состояние покоя тела по отношению к инерциальной системе отсчета, связанной обычно с условно неподвижным телом.
Свободным телом называется тело, движение которого в пространстве не ограничено другими телами. Реально окружающие нас тела являются несвободными, так как их перемещение в пространстве ограничено другими телами.
Тела, ограничивающие свободное перемещение рассматриваемого тела в пространстве, называются связями.
Сила, с которой связь действует на рассматриваемое тело, называется реакцией связи.
В теоретической механике рассматриваются покой или движение только свободных тел. Для этого отбрасывают наложенные на рассматриваемое тело связи и заменяют их реакциями связей. Это принцип освобождаемости от связей.
Совокупность сил, действующих на твердое тело, называется системой сил.
Эквивалентными называются системы сил оказывающие на рассматриваемое тело одинаковое воздействие.
Аксиомы статики

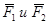
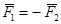
Система сил 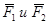
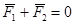
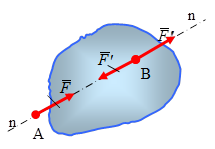

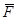

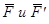
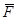
Аксиома 3. Две силы 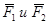
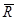
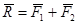
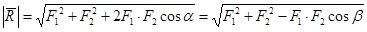
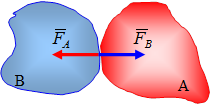
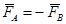
Но силы 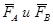
Аксиома 5.Равновесие деформируемого тела не нарушится, если тело считать отвердевшим (принцип отвердевания).
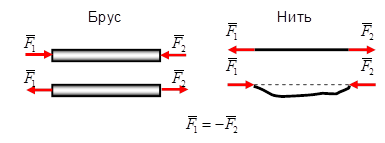
Условия равновесия, являющиеся необходимыми и достаточными для твердого тела,являются необходимыми, но недостаточнымидля деформируемого тела. Например, деформируемая нить находится в равновесии только, если силы 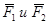
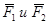
1.1.3 Две основные задачи статики:
1. Задача оприведении системы сил заключается в замене данной системы сил другой, наиболее простой, ей эквивалентной.
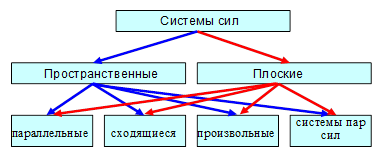
1.1.4 Классификация систем сил:
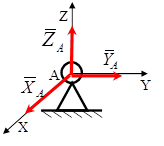
Виды связей
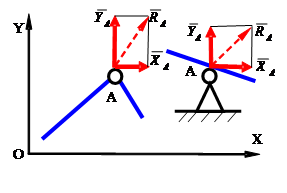
Рассмотрим наиболее часто встречающиеся типы связей и направления их реакций.
1.2.1 Связи, направления реакций которых заранее известно.
Гладкая поверхность (плоскость)
Реакция 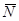
 |

Реакция 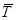

Реакция 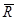
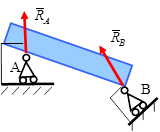
Реакция 
1.2.2 Связи, направления реакций которых неизвестны.
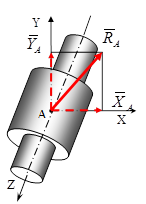
Реакция 
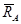
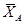

В аксонометрии – линиями параллельными оси шарнира со штриховкой.
 |

В зависимости от внешней нагрузки реакция шарового шарнира 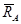



Жесткая заделка


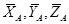
Поверхности
Простые поверхности.
Будем говорить, что функция \(f(u, v)\) непрерывно дифференцируема на замкнутом множестве \(E \subset \boldsymbol
Пусть \(\Omega\) — ограниченная область в \(\boldsymbol
$$
x = \varphi(u, v),\quad y = \psi(u, v),\quad z = \chi(u, v),\quad (u, v) \in \overline<\Omega>,\label
$$
называется непрерывно дифференцируемым.
Если при этом в каждой точке \((u, v) \in \Omega\) ранг функциональной матрицы
$$
\begin
$$
равен двум, то отображение \(F: \rightarrow \boldsymbol
Если \(\overline<\Omega>\) есть замкнутое ограниченное множество в \(\boldsymbol
Пусть область \(\Omega\) ограничена простым гладким или кусочно гладким контуром \(\gamma\). Образ кривой \(\gamma\) при гладком отображении \(F: \overline <\Omega>\rightarrow \boldsymbol
Если уравнение кривой \(\gamma\) имеет вид
$$
u = u(t),\quad v = v(t),\quad \alpha \leq t \leq \beta,\nonumber
$$
то уравнение \(\partial\Sigma\) задается следующими формулами:
$$
x = \varphi(u(t), v(t)),\quad y = \psi(u(t), v(t)),\quad z = \chi(u(t), v(t)),\quad \alpha \leq t \leq \beta.\label
$$
График функции \(z = f(x, y)\), непрерывно дифференцируемой на замкнутом ограниченном множестве \(\overline <\Omega>\subset \boldsymbol
$$
x = u,\quad y = v,\quad z = f(u, v),\quad (u, v) \in \overline<\Omega>.\label
$$
В этом случае матрица \(\begin
Например, график функции \(z = x^ <2>+ y^<2>\), \((x, y) \in \overline<\Omega>\), где \(\overline <\Omega>= \ <(x, y): x^<2>+ y^ <2>\leq 1\>\), есть простая поверхность. Окружность, получаемая при пересечении параболоида вращения \(z = x^ <2>+ y^<2>\) и плоскости \(z = 1\), является краем рассматриваемой простой поверхности.
Уравнения \eqref
$$
\boldsymbol
$$
С механической точки зрения формулы \eqref
Имея в виду приложения теории поверхностных интегралов, введем в рассмотрение класс почти простых поверхностей.
Пусть \(\Omega\) — плоская область и \(F: \overline <\Omega>\rightarrow \boldsymbol
Сфера \(S = \ <(x, y, z): x^<2>+ y^ <2>+ z^ <2>= a^<2>\>\) есть почти простая поверхность.
Образами отрезков \(\varphi = \varphi_<0>\), \(\displaystyle-\frac<\pi> <2>\leq \psi \leq \frac<\pi><2>\) являются меридианы, а при \(\displaystyle|\psi_<0>| Рис. 52.1
Конус \(K = \ <(x, y, z): x^<2>+ y^ <2>= z^<2>\>\) есть почти простая поверхность.
\(\vartriangle\) Введем цилиндрические координаты. Тогда конус \(K\) есть образ полуполосы
$$
\overline <\Omega>= \ <(r, \varphi): 0 \leq r Рис. 52.2
Легко проверить, что \(\overline<\Omega>_
Если \(\Sigma\) есть простая поверхность, заданная векторным уравнением \eqref
$$
u = u(u’, v’),\ v = v(u’, v’),\ (u’, v’) \in \Omega’\nonumber
$$
задают взаимно однозначное отображение замыкания области \(\Omega’\) на замыкание ограниченной области \(\Omega\), причем якобиан отображения
$$
\frac<\partial(u, v)> <\partial(u’, v’)>= \begin
$$
отличен от нуля в \(\overline<\Omega>’\), то уравнение
$$
\boldsymbol
$$
определяет ту же простую поверхность, что и уравнение \eqref
Как и в случае кривых, можно расширить класс параметризаций, допуская и такие замены параметров, при которых непрерывная дифференцируемость, взаимная однозначность и необращение в нуль якобиана отображения нарушаются на границе области. Тогда можно получить такие параметризации простой поверхности, задаваемые функциями, непрерывная дифференцируемость которых не имеет места на границе области \(\Omega\).
\(\vartriangle\) Переход от уравнений \eqref
$$
u = a \cos \varphi \cos \psi,\quad v = a \sin \varphi \cos \psi,\quad (\varphi, \psi) \in \Omega’.\label
$$
Якобиан отображения \eqref
Как правило, в дальнейшем для простых поверхностей будут рассматриваться только такие параметризации, которые задаются непрерывно дифференцируемыми на замкнутом ограниченном множестве функциями.
Криволинейные координаты на поверхности.
Пусть простая поверхность \(\Sigma\) задана векторным уравнением \eqref
$$
\boldsymbol
$$
лежащая на поверхности \(\Sigma\). Будем называть ее координатной кривой \(u = u_<0>\). Придавая \(u_<0>\) все значения из отрезка \([a, b]\), получим семейство координатных кривых \(u = \operatorname
Рис. 52.3
В силу взаимной однозначности отображения \eqref
Например, в сферических координатах часть сферы \(x^ <2>+ y^ <2>+ z^ <2>= a^<2>\), ограниченная двумя меридианами и двумя параллелями, задается в криволинейных координатах \(\varphi\), \(\psi\) следующим образом:
$$
\varphi_ <1>\leq \varphi \leq \varphi_<2>,\quad \psi_ <1>\leq \psi \leq \psi_<2>.\nonumber
$$
На сфере координатные кривые \(\varphi = \operatorname
На прямом круговом цилиндре координатными линиями будут образующие цилиндра и окружности, получающиеся при пересечении цилиндра плоскостями, перпендикулярными образующей.
Вектор-функция \(\boldsymbol
Если область \(\Omega\) не является выпуклой, а точка \((u_<0>, v_<0>)\) лежит внутри \(\Omega\), то нужно взять выпуклую окрестность точки \((u_<0>, v_<0>)\), лежащую внутри \(\Omega\). Тогда образ этой выпуклой окрестности будет куском поверхности \(\Sigma\) и координатные кривые можно строить на этом куске поверхности (локально).
Касательная плоскость и нормаль к поверхности.
Пусть \(\Sigma\) есть простая поверхность, заданная уравнениями \eqref
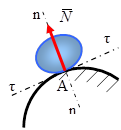
В любой точке \(A(u, v)\) простой поверхности \(\Sigma\) векторы \(\boldsymbol
\(\circ\) Рассмотрим вектор \(N = [\boldsymbol
$$
\boldsymbol
$$
Если \(\boldsymbol
$$
\boldsymbol
$$
то есть
$$
\boldsymbol
$$
Так как якобиан \(J = \displaystyle\frac<\partial(u, v)><\partial(u’, v’)>\) не обращается в нуль в области \(\Omega’\), то векторы \(\boldsymbol
Вектор нормали к простой поверхности \(\Sigma\) в точке \(A(u_<0>, v_<0>)\) ортогонален ко всем гладким кривым, лежащим на поверхности и проходящим через точку \(A(u_<0>, v_<0>)\).
\(\circ\) В самом деле, такая кривая есть образ при отображении \eqref
Уравнение кривой на поверхности тогда имеет вид
$$
\boldsymbol
$$
Касательный вектор \(\boldsymbol<\tau>\) к этой кривой в точке \(A\) есть
$$
\boldsymbol <\tau>= \frac
$$
Итак, \(\boldsymbol<\tau>\) есть линейная комбинация векторов \(\boldsymbol
Плоскость, проходящая через точку \(A(u, v)\) поверхности и ортогональная вектору \(\boldsymbol
$$
(\boldsymbol
$$
В силу равенства \eqref
$$
\begin
$$
Кусочно гладкие поверхности.
Из определения простой поверхности, данного в п. 1, следует, что она есть гладкий и взаимно однозначный образ некоторой плоской области, то есть получается из этой области при помощи гладких (без изломов) деформаций (отображений). Ясно, что многие объекты, которые мы привыкли называть поверхностями, не будут простыми поверхностями. Так, сфера не может быть непрерывным образом деформирована в плоскую область. Коническая поверхность не может быть получена гладкой деформацией плоской области.
Попытки дать общую классификацию поверхностей увели бы нас далеко в область высшей геометрии. Замечательным классом поверхностей в \(\boldsymbolРис. 52.4
Из гладких кусков можно склеивать не только гладкие многообразия, но и связные поверхности, имеющие ребра и вершины (например, поверхности многогранников) (рис. 52.5).
Рис. 52.5
Мы не станем тут заниматься математической формализацией таких понятий, как разрезание и склеивание поверхностей, и тем более основанной на этом классификации поверхностей. Заметим только, что трудности возникают при построении общих теорий. В любом разумном частном случае нет проблем с разрезанием поверхности на простые куски. Поверхность, которую можно разрезать на конечное число простых кусков, будем называть кусочно гладкой.
Ориентируемые поверхности.
Будем говорить, что гладкая поверхность ориентируема, если можно построить на этой поверхности непрерывное поле единичных нормальных векторов. Говорят, что это поле единичных нормалей определяет ориентацию (или сторону) поверхности. Меняя направление всех единичных нормалей на противоположное, получим опять непрерывное поле единичных нормальных векторов. Говорят, что оно определяет противоположную ориентацию (другую сторону) поверхности. На простой гладкой поверхности всегда определено непрерывное поле единичных нормальных векторов
$$
\boldsymbol
$$
Произвольные гладкие поверхности могут быть как ориентируемыми (двусторонними), так и неориентируемыми (односторонними).
Торы, изображенные на рис. 52.4, ориентируемы; бутылка Клейна — неориентируемая (односторонняя) поверхность. Легко построить лежащий на этой поверхности замкнутый гладкий контур такой, что, выбирая в какой-то точке контура вектор единичной нормали к поверхности и непрерывно изменяя его при движении по контуру, мы придем к начальной точке с противоположным направлением нормали. Следовательно, на бутылке Клейна построить непререрывное поле единичных нормальных векторов невозможно.
Заметим еще, что сфера, тор, тор с двумя дырами (рис. 52.4) делят пространство на ограниченную и неограниченную области, общей границей которых они являются. Бутылка Клейна таким свойством не обладает.
Можно доказать, что гладкая поверхность, являющаяся границей области в \(\boldsymbol
Рис. 52.6
Каждая плоскость делит пространство \(\boldsymbol
Рис. 52.7
Границу области \(G\), ориентированную внешними нормалями, будем обозначать через \(\partial G\), а внутренними — через \(\partial G^<->\).
Несколько более сложно определяется ориентация кусочно гладких поверхностей.
Рис. 52.8
Пусть \(\Sigma\) — простая поверхность (рис. 52.8), то есть гладкий и взаимно однозначный образ замыкания плоской области \(\Omega\). В декартовых координатах отображение задается равенствами \eqref
$$
\boldsymbol
$$
согласована с положительной ориентацией простых контуров, лежащих на поверхности \(\Sigma\).
Рис. 52.9
Покажем, что предложенное правило согласования ориентации поверхности с ориентациями простых контуров, лежащих на поверхности, совпадает с известным правилом правого винта. Пусть \(A(u_<0>, v_<0>) \in \Sigma\), то есть \((u_<0>, v_<0>) \in \Omega\). Без ограничения общности можно считать, что \(u_ <0>= 0\), \(v_ <0>= 0\). Построим в точке \(A\)(0,0) касательную плоскость и ориентируем ее вектором нормали \(\boldsymbol
$$
u = \varepsilon \cos t,\ v = \varepsilon \sin t,\ 0 \leq t \leq 2\pi.\nonumber
$$
Ее образ на поверхности есть простой замкнутый контур \(\Gamma\):
$$
\boldsymbol
$$
С точностью до \(\boldsymbol
$$
\boldsymbol
$$
С точностью до \(\boldsymbol
Ориентация эллипса положительна (рис. 52.10). Если смотреть на касательную плоскость со стороны вектора нормали \(\boldsymbol
Рис. 52.10
Пусть кусочно гладкая поверхность \(\Sigma\) склеена из гладких простых кусков \(\Sigma_<1>,\ \Sigma_<2>,\ \ldots,\ \Sigma_
Рис. 52.11
Можно показать, что кусочно гладкая поверхность, являющаяся границей ограниченной области, ориентируема, при этом каждый ее гладкий кусок можно ориентировать внутренними нормалями. В дальнейшем мы будем рассматривать только ориентируемые гладкие и кусочно гладкие поверхности.