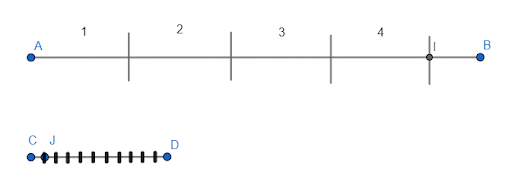
объясните что такое отрезок и концы отрезка

Как определяется понятие «отрезок» в геометрии

Содержание:

Для изображения прямых, лучей и отрезков применяют линейку. Отрезок на листике бумаги можно изобразить полностью, для луча и прямой – их фрагменты, ведь первый не имеет конца, только начало, вторая – бесконечна. Объясним, что такое отрезок в геометрии, чем отличается от иных фигур в евклидовом пространстве. Разберёмся с его свойствами.

Как выглядит отрезок

Обозначается двумя буквами – это название точек, лежащих в начале и конце. AB – концы геометрической фигуры, а расстояние между ними – длина фигуры, обозначается |AB|, измеряется преимущественно в сантиметрах.

Количество первых и вторых может быть любым.

Различают следующие отрезки:

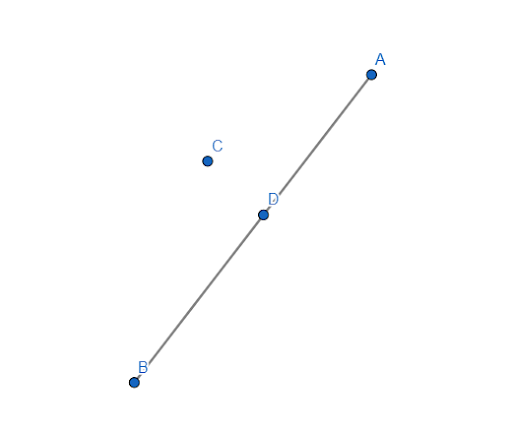
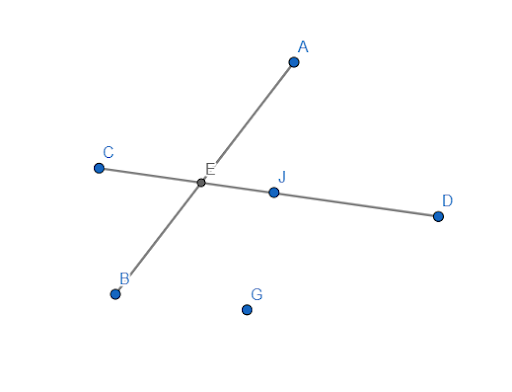
Выше показаны расположенные в одной точке пересекающиеся отрезки, имеющие общую точку – E. Два обрезка не могут иметь больше одной общей точки.

Разнообразие и измерение отрезков

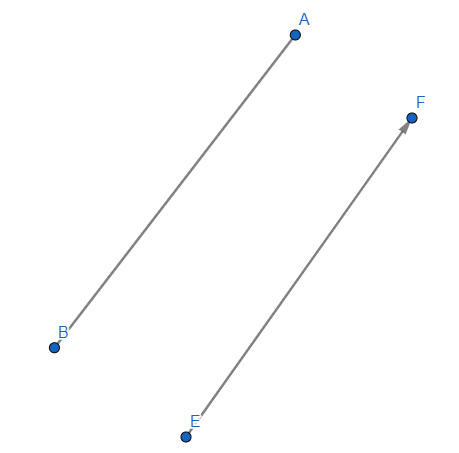
Геометрическая фигура AB тождественна или равная BA. Началом и концом может быть любая буква A или B, разницы нет. В случае с вектором фигура EF не равная FE.

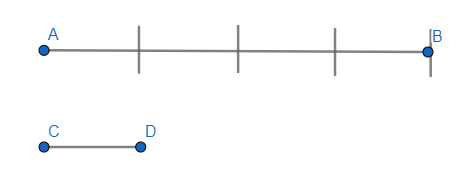
Измерение геометрических фигур основано на аксиоме Архимеда: дана пара отрезков разной длины, причём AB > CD. На AB можно отложить столько геометрических фигур CD, во сколько раз он меньше или короче AB.

CD. На AB можно отложить столько геометрических фигур CD, во сколько раз он меньше или короче AB.» src=»https://455811.selcdn.ru/BINGOCDN/default/moddocument/3023/e374aa7c42abc85c5922eca722ecfd2f1c4ee8aa.png» />

На практике их длина измеряется линейкой. Начальная точка совмещается с обозначением ноля на именительном приборе, точность которого равна одному миллиметру. Если конечная точка лежит между рисками на линейке, разницу в доли миллиметра не учитывают – значение округляют.

При измерении бывают следующие случаи (при условии, что AB > CD):

В подобных случаях обходятся избыточным и недостаточным измерениями. В первом – дробь округляют в меньшую сторону: если получается более 5,6, записывают 5,6; во втором – 5,7 см.

Источник

Отрезок

Определение отрезка

Определение 1. Отрезок (или отрезок прямой )− это часть прямой, ограниченная двумя точками.

Определение 2. Отрезок − это множество, состоящая из двух различных точек данной прямой и всех точек, лежащих между ними.

Точки, ограничивающие отрезки называются концами отрезка, а точки, которые находятся между концами отрезка называются внутренними точками.

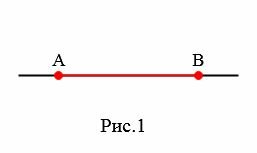На рисунке 1 отрезок выделен красным цветом. Точки A и B концы отрезка, а точки между ними − внутренние точки.

Обозначение отрезков

Отрезки обозначаются с помощью его конечных точек. Отрезок на рисунке 1 обозначается так: AB или BA. Порядок следования имен конечных букв не имеет значения.

Сравнение отрезков

Для сравнения отрезков нужно:

Если два других конца совместяться, то отрезки равны. Если же конец одного отрезка находится внутри другого, то длина первого отрезка меньше второго.

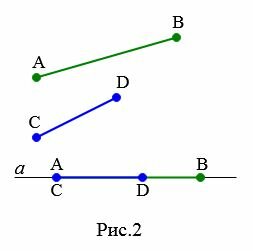Пусть даны два отрезка AB и CD (Рис.2). Требуется сравнить эти отрезки, т.е. определить какой из них больше. Отложим эти отрезки на прямой a. Как видим, точка D находится внутри отрезка AB. Значит отрезок CD меньше отрезка AB. Это обозначается так: CD Определение 3. Точка отрезка,делящая его на два равных отрезка называется серединой отрезка.

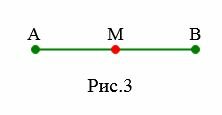На рисунке 3 \( \small M \) является серединой отрезка \( \small AB \) поскольку \( \small AM = MB \).

Длина отрезка

Для определения длины отрезка его нужно сравнить с другим отрезком, принятым за единицу измерения.

В качестве единицы измерения можно взять, например, сантиметр. В этом случае для определения длины отрезка узнают, сколько раз в данном отрезке укладывается сантиметр. Этот показатель и является длиной отрезка выраженная в сантиметрах. Если длина отрезка AB равна трем сантиметрам, то пишут AB=3см.

Если отрезок, принятый за единицу измерения не укладывается целое число раз в измеряемом отрезке, то его обычно делят на 10 равных частей и определяют сколько раз одна такая часть укладывается в остатке. Одна десятая часть сантиметра называется миллиметром. В итоге получаем длину отрезка в сантиметрах и миллиметрах.

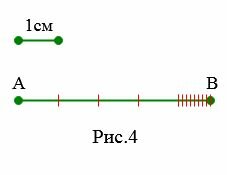На Рис.4 1см укладывается в отрезке AB 4 раза и в остатке укладывается ровно 8 одну десятую часть сантиметра. Поэтому можно писать: AB=4см 8мм или AB=4.8см.

Направленный отрезок

Если для отрезка определить направление, то такой отрезок называется направленным отрезком. Направленный отрезок имеет начальную точку и конечную точку. В конечной точке направленного отрезка рисуют стрелку (Рис.5)

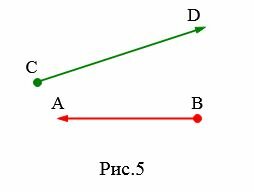Для обозначения направленных отрезков сначала пишется начальная точка, а затем конечная точка. На рисунке 2 верхний направленный отрезок обозначают так: \( \small \overrightarrow \) а нижний отрезок так: \( \small \overrightarrow \) Направленный отрезок называют вектором.

Источник

Урок 3 Бесплатно Отрезок. Длина отрезка

Начнем знакомство с одним из разделов математики, который называется геометрия.

Становление данной науки происходило тысячелетиями.

Сегодня обратим внимание на основные, базовые геометрические фигуры, такие как точка и отрезок.

Узнаем, что называют ломаной линией, какие геометрические фигуры называют многоугольниками, рассмотрим их основные элементы и характеристики.

Научимся сравнивать, находить длины отрезков.

Познакомимся с различными единицами измерения отрезков.

Рассмотрим свойства измерения длин отрезков.

Отрезок

Геометрическая фигура- это математическая модель, в которой рассматривается только форма и размер, не обращая внимания на иные свойства и состояния (цвет, из какого материала изготовлены, в каком состоянии находятся).

Как здания складываются из кирпичиков, так и сложные геометрические фигуры состоят из базовых фигур.

Одной такой элементарной фигурой является точка.

В реальности моделью, которая дает представление о точке может стать, например, след, оставленный острием карандаша, или отверстие на бумаге от швейной иглы.

Слово «точка» с латинского языка означает мгновенное касание, укол.

Точку принято рассматривать как некоторое место в пространстве или на плоскости.

Принято обозначать точки заглавными латинскими буквами (А, В, С и т.д.).

Две точки на плоскости можно соединить бесконечным множеством линий.

Самой короткой линией, соединяющей две точки на плоскости, будет прямая, проведенная по линейке через эти две точки.

Кратчайшая линия между двумя точками называется отрезком.

Любые две точки можно соединить только одним отрезком.

Точки, ограничивающие отрезок, называются концами отрезка.

Отрезок обозначают указанием имен его концов.

Через точки А и В с помощью линейки провели прямую.

Так как отрезок обозначают именами точек, получим отрезок АВ или ВА.

Пишут и говорят так: «Отрезок АВ» или «Отрезок ВА».

В названии отрезка не важно в каком порядке указываются его концы.

Отрезок можно построить с помощью линейки.

Для этого необходимо к отмеченным на плоскости точкам приложить линейку и провести прямую от одного конца отрезка до другого.

Чтобы с помощью линейки начертить отрезок, который длиннее чем сама линейка, нужно поступить следующим образом:

Между точками А и В отметить точку С.

Затем передвинем линейку так, чтобы левый конец линейки оказался около точки С, по правому концу линейки отложим точку D.

Последовательно соединив концы отрезков, получится отрезок AD, который длиннее, чем линейка.

У меня есть дополнительная информация к этой части урока!

Давайте разберемся, как могут располагаться точки по отношению к отрезку:

1. Точка лежит на отрезке.

Говорят: «Точка G принадлежит отрезку ».

Записывают это так: G ∈ AB

2. Точка не лежит на отрезке.

Говорят: «Точка не принадлежит отрезку ».

Записывают это так: R ∉ AB

Пройти тест и получить оценку можно после входа или регистрации

Длина отрезка

Каждый отрезок имеет определенную длину, значение которой является числом.

Так как каждый отрезок имеет длину, отрезки можно измерять и сравнивать.

Существует несколько способов сравнения отрезков.

1. Приблизительный способ сравнения.

Данный способ сравнения применяют только в том случае, когда длины отрезков явно отличаются.

Пример: Даны два отрезка АВ и ЕР

Очевидно, что отрезок АВ длиннее отрезка ЕР, значит, АВ > ЕР

Метод заключается в следующем: совмещаются два отрезка друг с другом так, чтобы совпали их концы с одной стороны.

По расположению других концов относительно друг друга можно оценить какой из отрезков длиннее, а какой короче.

Если при наложении отрезков друг на друга длины отрезков совпадут, то отрезки равны (отрезки в этом случае будут равными фигурами).

Если при наложении отрезков друг на друга один из отрезков будет составлять часть второго, то первый отрезок является короче второго (т.е. длина первого меньше длины второго).

Пример: Даны два отрезка АВ и ОЕ

Сравним данные отрезки методом совмещения отрезков.

Совместим левый конец А отрезка АВ и левый конец О отрезка ОЕ.

Можно заметить, что отрезок ОЕ составляет часть отрезка АВ.

Значит, отрезок ОЕ короче отрезка АВ.

Данный метод удобен, если есть возможность перемещать отрезки, совмещать один с другим.

3. Сравнение отрезков с помощью измерителя.

Если нет возможности перемещать сравниваемые отрезки, то можно использовать промежуточный измеритель.

В математике для этих целей используют специальный чертежный инструмент, который называется циркулем.

Чтобы сравнить отрезки с помощью циркуля, необходимо совместить концы отрезка с ножками циркуля.

Не меняя раствор циркуля, приложить его ко второму отрезку и сравнить.

Если нет возможности сравнить отрезки наложением и нет циркуля под рукой, то в качестве измерителя можно использовать нитку.

В таком случае нужно нитку приложить к исходному отрезку, на нитке по отрезку сделать замер, затем нитку приложить ко второму отрезку, оценить расположение замера на нитке по отношению к исследуемому отрезку, сделать вывод.

Пусть даны три отрезка СD, АЕ, BG

Сравним эти отрезки с помощью циркуля.

Соединим ножки циркуля с концами С и D отрезка СD.

Приложим циркуль с заданным раствором к отрезку АЕ.

Концы измерителя совпали с точками отрезка АЕ, значит, отрезки CD и AE равны: (CD = AE).

Приложим циркуль с заданным раствором к отрезку BG.

Отрезок выходит за концы измерителя, т.е. является частью отрезка BG, следовательно, отрезок BG длиннее отрезка СD: (BG > СD).

Все рассмотренные способы сравнения длины отрезков проводят без определения значения длины сравниваемых отрезков.

4. Существует еще один способ сравнения длины отрезков путем измерения их длинны.

Для этого необходимо сначала измерить длину каждого отрезка, далее сравнить полученные значения их длины и сделать вывод.

Большим будет являться тот отрезок, длина которого больше.

Соответственно, если длины измеряемых отрезков равны, то и отрезки равны.

У меня есть дополнительная информация к этой части урока!

Ломаная линия

Если последовательно соединить отрезки так, чтобы конец одного отрезка являлся началом следующего (при этом соседние отрезки не лежат на одной прямой), то образуется геометрическая фигура, которая называется ломаной линией.

Отрезки, из которых состоит ломаная линия, называют звеньями.

Концы отрезков называют вершинами ломаной.

Самые крайние вершины ломаной называют концами ломаной

Обозначение ломаной линии составляют из названий вершин этой ломаной, называя их по порядку.

Длиной ломаной называется сумма длин всех ее звеньев.

На рисунке изображена ломаная линия АBCDE.

Вершины ломаной АBCDE: А, B, C, D, Е.

Звенья ломаной АBCDE: AB, BC, CD, DE.

Найдем длину ломаной АВСDE:

АВСDE = AB+ BC+ CD+ DE = 2 см + 3 см + 4 см + 5 см = 14 см

Ломаная, концы которой совмещаются, называется замкнутой.

Многоугольником называется фигура, ограниченная замкнутой ломаной линией, звенья которой не пересекаются.

Отрезки (звенья) ломаной линии называют сторонами многоугольника.

Общие точки двух отрезков (сторон) многоугольника называют его вершинами.

Каждая пара сторон многоугольника, сходящиеся в одной точке, образуют углы многоугольника.

Количество сторон и количество углов в многоугольнике совпадают.

Вершины, стороны и углы многоугольника обозначаются аналогично ломаной линии.

Многоугольник принято обозначать и называть по его вершинам, начиная с любой вершины и называя их последовательно, в любом порядке.

На рисунке изображен многоугольник АBCDEF.

Вершины многоугольника АBCDEF: А, B, C, D, Е, F.

Стороны многоугольника АBCDEF: AB, BC, CD, DE, EF, FA.

Любые многоугольники можно сравнить: два многоугольника называются равными, если они совпадают при наложении.

Зная длину каждой стороны многоугольника, можно найти периметр этого многоугольника.

Периметр многоугольника принято обозначать заглавной латинской буквой Р

Найдем периметр многоугольника АBCDEF (изображенного на рисунке):

Р_АВСDEF = AB+ BC+ CD+ DE+ EF+ FA = 2 см + 3 см + 2 см + 2 см + 3 см + 2 см = 14 см.

Существует огромное множество различных видов многоугольников.

Обычно многоугольники различают по числу сторон и углов.

Многоугольник с наименьшим числом вершин, сторон и углов называют треугольником.

Треугольник часто обозначают символом «Δ» и тремя заглавными латинскими буквами, которые обозначают его вершины.

На рисунке изображен треугольник АBC (Δ АBC).

Отрезки AB, BC, АC— стороны треугольника АBC.

Периметр треугольника- это сумма длин трех его сторон.

Найдем периметр треугольника АBC (изображенного на рисунке):

Р_АВС = AB+ BC+ АС = 4 см + 6 см + 3 см = 13 см.

Пройти тест и получить оценку можно после входа или регистрации

Источник

Объясните что такое отрезок и концы отрезка

На этом уроке учитель продолжит разговор о линиях и точках, расскажет, что такое отрезок, как он обозначается. Также вы узнаете о четырех способах сравнения отрезков и узнаете о единицах измерения длины. В конце урока вы вместе с учителем потренируетесь решать задачи, используя единицы измерения длины.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Измерение» и «Связь числа и геометрии. Часть 1. Измерения в геометрии. Свойства фигур»

Если заданы точка и линия, то точка либо принадлежит этой линии, либо нет. Еще говорят, что линия проходит через точку.

На рисунке 1 точка не принадлежит линии , или линия не проходит через точку . Точка принадлежит линии , или линия проходит через точку .

Рис. 1. Линия и точки: принадлежащие линии и не принадлежащие

Пусть у нас есть две точки и (рис. 2). Сколько можно провести линий, которые будут проходить через обе эти точки? Или сколькими линиями можно соединить эти две точки? Бесконечное количество.

Рис. 2. Точки и

Точки и могут обозначать два места, например дом и школу. А линии, их соединяющие, – траекторию, по которой можно пройти от дома до школы (рис. 3). Часто интересует самая короткая дорога от дома до школы, от одного места до другого, от точки до точки .

Рис. 3. Дорога от дома до школы как отрезок

Какая дорога от школы до дома самая короткая? Какая линия, соединяющая и , будем самой короткой?

Чтобы дорога оказалась самой короткой, идти от школы до дома надо по прямой. Чтобы линия, соединяющая точки, оказалась самой короткой, соединять их нужно по прямой.

Соединим и самой короткой возможной линией. Такая линия называется отрезком (рис. 4). Точки и называются концами отрезка.

Рис. 4. Точки и – концы отрезка

Обозначается сам отрезок , по именам точек – концов отрезка. Другой такой же короткой линии, соединяющей и , не существует. Если провести из в любую другую линию, она обязательно окажется длиннее. То есть существует только одна кратчайшая линия между и . Она и называется отрезком.

Если мы хотим указать на другие линии, соединяющие наши точки, например верхние или нижние, то нужно добавить еще точки, чтобы не было путаницы (рис. 5).

Рис. 5. Линии и , соединяющие точки и

Если две точки и необходимо соединить отрезком, то используется линейка. Линия, проведенная по линейке от точки до точки по линейке, и будет нужным отрезком (рис. 6). Сам отрезок будет называться . Точки и – его концами. Отрезок является кратчайшей линией, соединяющей точки и .

Рис. 6. Построение отрезка с помощью линейки

Любая точка либо принадлежит отрезку, либо не принадлежит.

Или говорят еще: «точка лежит на отрезке либо не лежит на отрезке». На рисунке точки и не принадлежат отрезку , точка принадлежит отрезку (рис. 7).

Рис. 7. Точки, принадлежащие и не принадлежащие отрезку

Сами точки и , концы отрезка, тоже принадлежат отрезку .

Посмотрим на два отрезка на рисунке 8. Что про них можно сказать? Отрезок короче отрезка (рис. 8). .

Рис. 8. Отрезки и

Как мы это поняли? Просто увидели. То есть сравнить эти два отрезка оказалось несложно.

Задача сравнения отрезков, их длины встречается в жизни достаточно часто. Например, два человека хотят выяснить, чей рост больше, кто из них выше.

Он подходит, если отрезки сильно отличаются и ответ однозначен.

Очевидно, что на рисунке 9 отрезок больше, длиннее, чем отрезок .

Очевидно, что папа выше сына.

Рис. 9. Сравнение роста папы и сына

Очевидно, что телебашня выше дерева на рисунке 10.

Рис. 10. Сравнение высоты телебашни и дерева

Этот способ очень прост, но может привести к ошибке.

Иногда, когда мы смотрим на картинку, то мы совершенно уверены, что понимаем, какой из двух отрезков больше. Но оказывается, что мы ошибаемся, потому что дополнительные построения вокруг отрезков обманывают зрение.

На картинке 1 нам кажется, что верхний отрезок длиннее нижнего.

Рис. 10.2. Иллюзия: кажется, что отрезки разной длины

Но это не так. В этом легко убедиться, если построить еще две линии.

Рис. 10.3. Одинаковые отрезки

Один из самых простых примеров ошибки восприятия. Какой отрезок короче на рисунке 3?

Рис. 10.4. Иллюзия: кажется, что отрезки не равны по длине

«Конечно же, первый!» – говорит наше восприятие. Но это не так. Эти отрезки одинаковые. В этом можно будет убедиться, воспользовавшись любым из остальных способов сравнения отрезков, которые мы рассматриваем на нашем сегодняшнем уроке.

Сложно поверить, что отрезки и равны. Дополнительные линии вокруг заставляют нас поверить, что отрезок намного короче отрезка на рисунке 4.

Рис. 10.5. Иллюзия: отрезки и имеют одинаковую длину

Все рассмотренные картинки являются примерами оптических иллюзий. Наберите в поисковой системе «оптические иллюзии», и вы найдете огромное количество очень интересных примеров по этой теме. Не только про сравнение отрезков.

Ну а мы с вами делаем главный вывод из этих примеров: не всегда можно доверять нашей оценке «на глаз». Нужны более точные методы сравнения отрезков.

Если бабушка хочет понять, одинаковы ли две спицы по длине, то она возьмет их вместе, зажмет в руку и несильно стукнет ими по столу, чтобы нижние края спиц оказались на одном уровне (рис. 11). По положению верхних краев она поймет, одинаковы ли спицы, если нет, то какая из них длиннее.

Рис. 11. Проверка с помощью наложения

Такой способ можно использовать, если предметы, которые мы сравниваем, можно легко приложить один к другому. Например, для сравнения роста люди встают спиной друг к другу и смотрят, чья макушка окажется выше.

Итак, метод заключается в том, что два предмета прикладывают друг к другу, совмещают концы с одной стороны и по положению других концов понимают, какой отрезок больше или, может быть, они равны.

Этот метод уже является точным, в отличие от первого. Но у него есть один серьезный недостаток. Чтобы им воспользоваться, нужно иметь возможность взять один отрезок и переместить, приложить его ко второму. Это не всегда возможно.

Ведь даже если нарисованы два отрезка, затруднительно взять один из них и приложить к другому. Если только разрезать лист, сложить части друг с другом и посмотреть на просвет.

Если один предмет мы не можем приставить к другому, то можно использовать третий, который легко совмещается с первым и вторым по очереди. Таким измерителем часто являются наши руки.

Если мы хотим понять, пройдет ли диван в дверной проем, мы руками отмечаем его ширину и, стараясь не изменить расстояние между руками, подходим к дверному проему и проверяем, хватит ли ширины дверей.

Мы можем использовать веревку, нитку, палку, чтобы сравнить длины двух предметов, которые сложно перемещать. Приложить нитку к одному предмету, потом ее же к другому. Так сразу будет понятно, какой из предметов длиннее. В математике для этой цели используются специальный измеритель, циркуль.

Нужно сравнить два отрезка и (рис. 12).

Рис. 12. Отрезки для сравнения

Совмещаем концы отрезка с иголками измерителя (рис. 13) и, не меняя раствора, сравниваем с другим отрезком (рис. 14).

Рис. 13. Измерение отрезка

Рис. 14. Измерение отрезка

Отрезок равен отрезку .

Записывается это так: .

Или может оказаться такая ситуация (рис. 15).

Рис. 15. Отрезки для сравнения

Отрезок не равен отрезку . Он равен отрезку , который является частью отрезка (рис. 16).

Рис. 16. Отрезок равен части отрезка

Отрезок меньше отрезка , так как является его частью.

Отрезок меньше отрезка , потому что равен его части.

Во всех предыдущих способах мы сравнивали отрезки, выясняли, у кого из них длина больше. Но саму длину не измеряли. Мы ее не знали.

Так, два человека могут встать друг другу спиной и выяснить, кто из них выше. Но каков рост каждого из них, они не узнают.

Последний способ, который мы сейчас рассмотрим, заключается в том, чтобы измерить длину каждого отрезка и сравнить их длины.

Так, если два человека знают, что рост одного составляет 1 м 73 см, а другого – 1 м 75 см, то понятно, что второй выше, и не нужно вставать рядом, чтобы это понять.

Длина, выраженная числом, то есть измеренная, становится очень удобным инструментом. Мы теперь эту длину можем записать, передать по телефону, запомнить.

Чтобы измерить отрезок, нужно приложить к нему линейку с нанесенной шкалой.

На рисунке 17 мы видим, что длина первого отрезка составляет 6 см, второго – 7 см.

Рис. 17. Измерение отрезков линейкой

Второй отрезок больше. Кроме того, мы теперь знаем, что второй не просто больше, а больше на 1 см.

А что если один отрезок измерял один человек, а второй – другой человек, да еще и в другом городе? Можно ли будет сравнить эти два отрезка? Да, это возможно потому, что на всех линейках нанесены одинаковые деления и не важно, какой конкретно линейкой мы пользовались. Скорее всего, на всех таких линейках мы увидим одинаковые деления – сантиметры и миллиметры.

Одна из самых часто встречающихся единиц длины – это метр.

Метр используется при измерении объектов не маленьких, но и не огромных, таких, которые можно оценить на глаз, увидеть сразу целиком: длина комнаты или двора, высота дерева или дома, расстояние от дома до школы и так далее. Сокращенно метр обозначается буквой «м». Точка, обозначающая сокращение, не нужна.

Все остальные единицы для измерения либо очень больших объектов, либо намного меньших получаются из метра.

Приставка «кило-» означает тысячу. Если перед словом метр поставить приставку «кило-», то полученное слово «километр» будет обозначать тысячу метров.

Сам километр кратко обозначается двумя буквами «км», тоже без точки для сокращения.

В километрах мы меряем большие расстояния, например расстояния между городами.

Если соединить центры Москвы и Санкт-Петербурга воображаемым отрезком (рис. 18), то его длина будет равна 635 км, или 635 000 метров.

Рис. 18. Отрезок между Москвой и Санкт-Петербургом

Для измерения длин небольших объектов используют более мелкие единицы. Разделим 1 метр на 10. Чтобы получить название этой единицы длины, поставим приставку «деци-» перед словом «метр».

Приставка «деци-» означает одну десятую, что в десять раз меньше. Обозначается дециметр буквами «дм».

Разделим 1 метр на 100. Чтобы получить название этой единицы длины, поставим приставку «санти-» перед словом «метр». Приставка «санти-» означает одну сотую, что-то, в сто раз меньшее. Обозначается сантиметр буквами «см».

Разделим 1 метр на 1000. Чтобы получить название этой единицы длины, поставим приставку «милли-» перед словом «метр». Приставка «милли-» означает одну тысячную, что-то, в тысячу раз меньшее. Обозначается миллиметр буквами «мм».

Кроме понимания, сколько в 1 метре содержится дециметров, сантиметров и миллиметров, полезно запомнить и соотношения напрямую между соседними единицами.

Мы делили метр на 10, 100 и 1000 частей. Но это равносильно делению на 10 уже полученных единиц. То есть поделили метр на 10, получили дециметр. Поделили еще раз на 10, получили сантиметр. Еще раз на 10, получили миллиметр.

Посмотрим еще раз на все эти единицы измерения вместе. Метр примерно можно получить как расстояние от плеча одной руки до вытянутых кончиков пальцев другой руки (рис. 19).

Рис. 19. Расстояние от плеча одной руки до конца второй руки примерно равно метру

На рисунке 20 деления на верхней линейке – сантиметры. В 1 метре 100 сантиметров. На нижней линейке сантиметры разделены на 10 делений. Это миллиметры.

Рис. 20. Линейки с различными шкалами

Дециметры обычно не отмечают на линейках и не делают для них специальных делений. Так сложилось, что в жизни редко используют эту величину. Мы почти не слышим слова «дециметр», хотя слова «сантиметр» и «миллиметр» можем услышать достаточно часто. В различных задачах эта единица бывает часто, и, чтобы решать их, нужно обязательно помнить, что это такое.

Рост человека измеряют или только в сантиметрах, или метрах и сантиметрах. Если рост человека составляет 1 м 75 см, то каков его рост в сантиметрах?

Так как 1 м равен 100 сантиметрам, то рост равен .

Рост Петра Первого составлял 203 см. Как его рост записать другим способом?

Дорога длиной 3 км и шириной 2 м 40 см выложена квадратной плиткой со стороной 6 дм. Сколько плиток понадобилось, чтобы выложить всю дорогу?

Рассмотрим рисунок 21.

Рис. 21. Иллюстрация к задаче

Найдем сначала, сколько плиток помещается в ширину дороги.

Для этого нужно ширину дороги разделить на размер стороны плитки, но перед этим нужно указать эти размеры в одинаковых единицах измерения.

В одном метре 10 дм, следовательно, 2 метра – это 20 дм. 10 сантиметров – это 1 дециметр, следовательно, 40 см – это 4 дм.

Получаем: .

В ширину дороги укладывается То есть дорожка в 4 раза шире, чем плитка. Значит, в ширину помещается 4 плитки.

Теперь посчитаем, сколько плиток помещается в длину.

Длина дороги составляет 30 000 дм. Разделим эту длину на размер плитки, на 6 дм.

Итак, в длину помещается 5000 плиток, а в ширину – 4 штуки.

Всего необходимо плиток.

Список литературы

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Домашнее задание

Источник