что значит зона незначимости в критерии манна уитни
Основные статистические критерии. Непараметрический критерий Манна-Уитни (U-критерий Манна — Уитни,. Mann–Whitney U-test). Понятие и порядок практического использования
При проведении психологических исследований важно уметь пользоваться не только информацией, но и грамотно ее преобразовывать, интерпретировать и анализировать в целях получения достоверного результата.
При проведении психологических исследований важно уметь пользоваться не только информацией, но и грамотно ее преобразовывать, интерпретировать и анализировать в целях получения достоверного результата.
Одной из распространенных практических методик, позволяющих систематизировать имеющиеся материалы и проанализировать их, является непараметрический критерий манна-Уитни. Этот механизм пришел в психологическую науку из статистики и успешно используется вплоть до настоящего времени.
Зачем необходим критерий Манна-Уитни?
Научно-исследовательский проект по психологии предполагает изучение конкретных объектов с целью установления сходств и различий, особенностей поведения и иных мотивов. Зачастую в качестве объекта научных изысканий выступают отдельные индивиды или целые группы ли, разбитые на несколько групп по определенным признакам. В целях упрощения анализа данных исследователь изучает средние значения конкретных критериев, коэффициентов или «симптомов».
Расчет «среднего» значения производится аналогично среднему арифметическому: суммируют показатели всех испытуемых и делят на количество испытуемых объектов исследования.
Далеко не всегда анализ показателей испытуемых позволяет сделать определенный вывод. Если в исследовании принимает участие всего 2 объекта со схожими параметрами, то получить результат и вывод можно легко. Но если речь идет о группе лиц с разными критериями, то задача усложняется. Решить ее становится возможно при помощи специальной статистической методики «различий». Именно к этому виду относят критерий Манна-Уитни.
Данный механизм позволяет определить степень совпадения или несовпадения в отношении разных выборок, объектов исследования.
Суть непараметрического критерия Манна-Уитни
На сегодняшний день благодаря развитию НТП рассчитывать критерий U-test можно с помощью специальных сервисов: Ststistica, SPSS. Но при написании студенческих и научных работ студенты чаще используют «ручной способ».
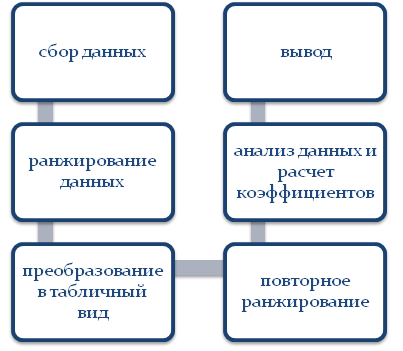
Рассмотрим действие алгоритма на конкретном примере. Допустим, исследователь намерен оценить уровень обеспокоенности (взволнованности, тревожности) у разнополых объектов. В каждой группе будет принимать участие по 10 человек. У каждого индивида зафиксирован определенный уровень обеспокоенности, который был оценен по 10-балльной шкале. Исследователю важно определить, сильно ли отличается значение исследуемого параметра мужчин и женщин. Для этого достаточно следовать по этапам:
Нужна помощь преподавателя?
Мы всегда рады Вам помочь!
Использование специальных программ для расчета критерия Манна-Уитни позволяет в считанные минуты провести численный анализ и представить результаты в виде графиков, где будет очевидно пересечение или не пересечение исследуемых групп. Программа укажет два важных параметра:
В ходе использования непараметрического критерия U-test важно учесть определенные ограничения: количество испытуемых лиц не должно превосходить 60, минимальное количество объектов исследования – 3. Выборка может быть равномерной или неравномерной. Сравнивать можно самые разные показатели (психологические и непсихологические), главное располагать нужными данными.
Пример использования критерия Манна-Уитни в психологическом исследовании
Команда Дисхелп готова выполнить студенческую или научно-исследовательскую работу по психологии. Наши специалисты помогут в формировании информационной базы проекта, проведении эксперимента и анализа полученных данных. У нас работают преподаватели ведущих ВУЗов, кандидаты и доктора наук, практикующие эксперты. Мы гарантируем соблюдение дедлайнов и всех заявленных заказчиком требований. Высокое качество, конфиденциальность данных и индивидуальный подход – всегда в нашем арсенале. Убедитесь в этом лично, оформив заявку на нашем сайте.
Трудности с учебой?
Помощь в написании студенческих и
аспирантских работ!
ПРАВИЛО ОТКЛОНЕНИЯ НУЛЕВОЙ И ПРИНЯТИЯ АЛЬТЕРНАТИВНОЙ ГИПОТЕЗЫ
Если эмпирическое значение критерия равняется критическому значению, соответствующему a £ 0,05, или превышает его, то Н0 отклоняется, но мы еще не можем определенно принять Н1.
Если эмпирическое значение критерия равняется критическому значению, соответствующему a £ 0,01, или превышает его, то Н0 отклоняется и принимается Н1.
Исключения составляют критерий знаков G, критерий Т Вилкоксона и критерий U Манна-Уитни. Для них устанавливаются обратные соотношения.
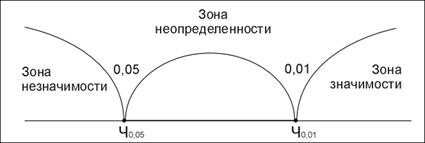
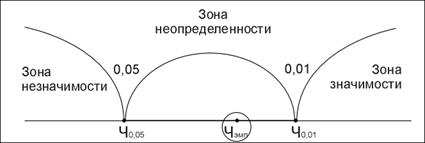
Для облегчения процесса принятия решения можно всякий раз вычерчивать «ось значимости»:
«Ось значимости» представляет собой прямую, на левом конце которой располагается 0, хотя он, как правило, не отмечается на самой этой прямой, и слева направо идет увеличение числового ряда. По сути дела это привычная школьная ось абсцисс ОХ декартовой системы координат. Однако особенность этой оси в том, что на ней выделено три участка, «зоны». Левая зона называется «зоной незначимости», правая – «зоной значимости», а промежуточная – «зоной неопределенности». Границами всех трех зон являются критическое значение, соответствующее a£0,05 (обозначается как Ч0,05 )и критическое значение, соответствующее a£0,01 (обозначается как Ч0,05 ).
Вправо от критического значения Ч0,01 простирается «зона значимости» – сюда попадают эмпирические значения, превышающие Ч0,01, и, следовательно, значимые. В этом случае принимается альтернативная гипотеза H1:
Влево от критического значения Ч0,05 простирается «зона незначимости» – сюда попадают эмпирические значения, которыениже Ч0,05 следовательно, незначимы, и в этом случае принимается гипотеза Н0 об отсутствии различий:
Если эмпирическое значение попадает в «зону неопределенности», то отклоняется гипотеза о недостоверности различий (Н0), но гипотеза об их достоверности (Н1) не принимается:
Практически, однако, исследователь может считать достоверными уже те различия, которые попадают в «зону неопределенности», заявив, что они достоверны при a £ 0,05, или указав точный уровень значимости полученного эмпирического значения критерия, например: a=0,02.
Уровень статистической значимости или критические значения критериев определяются по-разному при проверке направленных и ненаправленных статистических гипотез.
При направленной статистической гипотезе используется односторонний критерий, при ненаправленной гипотезе – двусторонний критерий. Двусторонний критерий более строг, поскольку он проверяет различия в обе стороны, и поэтому то эмпирическое значение критерия, которое ранее соответствовало уровню значимости a£0,05, теперь соответствует лишь уровню a£0,10.
Задача 7.1
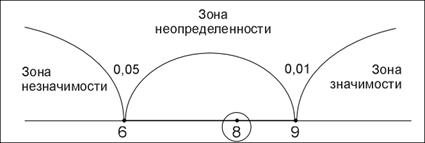
Пусть критические значения критерия Q-Розенбаума соответственно равны 6 и 9и обозначаются как Q0,05=7 и Q0,01=9. Принята следующая стандартная форма записи критических значений:

Допустим, эмпирическое значение критерия равно 8: Qэмп=8. На «оси значимости» эмпирическое значение заключено в эллипс:
Эмпирическое значение критерия в нашей задаче попадает в область между Q0,05 и Q0,01, и мы можем считать различия достоверными при a£0,05.
МОЩНОСТЬ КРИТЕРИЕВ
Мощность критерия – это его способность выявлять различия, если они есть. Иными словами, это его способность отклонить нулевую гипотезу об отсутствии различий, если она неверна.
Ошибка, состоящая в том, что мы приняли нулевую гипотезу, в то время как она неверна, называется ошибкой II рода.
Вероятность такой ошибки обозначается как b. Мощность критерия – это его способность не допустить ошибку II рода, поэтому мощность равна 1- b.
Мощность критерия определяется эмпирическим путем. Одни и те же задачи могут быть решены с помощью разных критериев: при этом обнаруживается, что некоторые критерии позволяют выявить различия там, где другие оказываются неспособными это сделать, или выявляют более высокий уровень значимости различий. Возникает вопрос: а зачем же тогда использовать менее мощные критерии? Дело в том, что основанием для выбора критерия могут быть не только мощность, но и другие его характеристики, а именно простота, более широкий диапазон использования, применимость по отношению к неравным по объему выборкам, большая информативность результатов.
? ВОПРОСЫ И УПРАЖНЕНИЯ
5. Дайте определение следующим понятиям:
§ нулевая и альтернативная гипотезы;
§ ошибка первого рода, ошибка второго рода;
§ уровень статистической значимости;
2. Охарактеризуйте параметрические и непараметрические методы.
3. Воспроизведите правило отклонения нулевой гипотезы или принятия альтернативной.
4. Критические значения c 2 (критерий Пирсона) по статистическим таблицам соответственно равны:
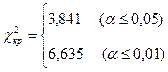
Исходя их критических значений, сформулируйте принятие решения (выберите соответствующую гипотезу – H0 или Н1) для следующих эмпирических значений:
§ 
§ 
§
§ 
II. Критерий U- Манна-Уитни
ОСЬ ЗНАЧИМОСТИ
Для принятия решения, какую гипотезу выбрать, используют ось значимости.
зона незначимости зона неопределенности зона значимости





Ккрит находятся по таблице критических значений, которые есть для каждого критерия.
СОПОСТАВЛЕНИЕ СОВОКУПНОСТЕЙ
ПО УРОВНЮ ПРИЗНАКА
I. Критерий Q Розенбаума
Qкр находим по таблице критических значений в зависимости от n1 и n2.
Далее с помощью оси значимости определяем, какую гипотезу принять, а какую отвергнуть.
зона незначимости зона неопределенности зона значимости





Графически данный критерий Q можно представить следующим образом:

1. В каждой из выборок не менее 11 испытуемых, при этом n1 ≈ n2:
2.Диапазоны разброса значений в двух выборках не должны совпадать.
3. При n1, n2 > 26 полученное эмпирическое значение сопоставлять с Qкр=8 (р≤0,05) и Qкр=10 (р≤0,01).
II. Критерий U- Манна-Уитни
В отличии от критерия Q этот метод используют, когда ряды «налагаются» частично друг на друга.
Графически данный критерий можно представить следующим образом:
При применении критерия:
1) упорядочить значения признака,
2) необходимо их проранжировать, одновременно оба ряда.
3) подсчитать сумму рангов отдельно для каждой выборки, сравнить, совпадает ли общая сумма рангов с расчетной.
Uэмп= n1 

где Rx – большая из двух ранговых сумм, а nх – объем выборки с большей ранговой суммой.
5) Uкр найти по таблице критических значений в зависимости от n1 и n2.
6) с помощью оси значимости определить, какую гипотезу принять, а какую отвергнуть. Но так как, чем меньше Uэмп, тем более достоверны различия, зоны на оси значимости поменяются местами. Этот критерий – исключение.
зона значимости зона неопределенности зона незначимости





1. В каждой выборке должно быть не менее 3 наблюдений; допускается в одной 2 наблюдения, но тогда во второй не менее 5.
2. В каждой выборке n1,n2≤60 (из-за сложности ранжирования большого количества данных).
Пример. Две группы испытуемых решали задачу. Показателем успешности служило время решения. Одна из групп получала дополнительную мотивацию в виде денежного вознаграждения. Вопрос: влияет ли денежное вознаграждение на успешность решения задачи?
| группа без доп. мотвац. | суммы |  | ||||||||
| 111,5 | ||||||||||
| ранги R1 | 4,5 | 6,5 | 11,5 | 15,5 | ||||||
| группа с доп мотвац. | 106,4 | |||||||||
| ранги R2 | 4,5 | 6,5 | 11,5 | 11,5 | 11,5 | 15,5 | 20,5 | 20,5 | 22,5 | 22,5 |
H0: решение задачи в группе с дополнительной мотивацией не успешнее, чем в группе без мотивации.
H1: решение задачи в группе с дополнительной мотивацией успешнее, чем в группе без мотивации.
1. Критерий Q Розенбаума.
2. Критерий U Манна-Уитни
Проранжируем два ряда значений.
Общая сумма рангов 189+162=351.
Расчетная сумма Σ R = N(N+1)/2=26(26+1)/2=351.
Uэмп=12 

По таблице критических значений по n1=12, n2=14 находим







U-критерий Манна-Уитни
U-критерий Манна-Уитни чаще всего используется при обработке результатов эмпирического исследования при написании курсовых, дипломных и магистерских работ по психологии.
U-критерий Манна-Уитни – непараметрический статистический критерий. Это означает, что его требования к группам и измеренным психологическим показателям минимальны:
Как рассчитывается U-критерий Манна-Уитни
Не вдаваясь в математические тонкости, рассмотрим логику расчёта U-критерия Манна-Уитни.
Например, в результате тестирования были получены интегральные показатели осмысленности жизни замужних и незамужних женщин. Одной из задач дипломной работы ставится выявление различий осмысленности жизни у женщин, состоящих и не состоящих в браке. Выборки небольшие (по 30 человек), поэтому можно использовать U-критерий Манна-Уитни.
Процедура расчёта U-критерия Манна-Уитни в самом общем и приближенном виде выглядит следующим образом:
При расчете U-критерия Манна-Уитни с помощью статистических программ выдается значение самого критерия и уровень статистической значимости различий выраженности психологического показателя. Эти показатели необходимо занести в таблицу и выделить те психологические показатели, уровень значимости различий которых в группах ниже, чем 0,05.
Пример расчета U-критерия Манна-Уитни вручную
В результате психодиагностического обследования групп мужчин и женщин (по 20 человек в каждой) были выявлены показатели внутреннего сопротивления при обращении в службу знакомств (в баллах):
Выдвигаем гипотезу о том, что существуют различия внутреннего сопротивления при обращении в службу знакомств между мужчинами и женщинами.
Для проверки гипотезы будет использовать непараметрический критерий U-критерий Манна-Уитни.
Проведем ранжирование показателей в группах мужчин и женщин от меньшего к большему и занесем данные в таблицу.
Пример расчета критерия U Манна-Уитни
Допустим мы хотим сравнить уровень интеллекта детей в 7 «а» и 7 «б» классе средней общеобразовательной школы. Для сравнения двух выборок между собой воспользуемся критерием U Манна-Уитни.
Шаг 1. Занесем значения в таблицу.
| 7 «а» | 7 «б» | ||
| ФИО Испытуемого | Баллы IQ | ФИО Испытуемого | Баллы IQ |
| КТИ | 112 | БРИ | 121 |
| ВСИ | 105 | ДРО | 120 |
| МНИ | 109 | РНА | 134 |
| АНМ | 90 | ВРА | 119 |
| УРА | 130 | ГРА | 115 |
| ВФЫ | 117 | ДЖА | 106 |
| РКИ | 117 | ВЦК | 107 |
| ТРИ | 125 | ЮЕР | 101 |
| ТРК | 134 | ЖЕН | 97 |
| ТНК | 109 | КОР | 117 |
Шаг 2. Расположим все значения в один ряд (2.1) и проранжируем их (2.2).
| ФИО Испытуемого | Баллы IQ (2.1) | Ранг (2.2) |
| РНА | 134 | (1+2)/2=1,5 |
| ТРК | ||
| УРА | 130 | 3 |
| ТРИ | 125 | 4 |
| БРИ | 121 | 5 |
| ДРО | 120 | 6 |
| ВРА | 119 | 7 |
| ВФЫ | 117 | (8+9+10)/3=9 |
| РКИ | ||
| КОР | ||
| ГРА | 115 | 11 |
| КТИ | 112 | 12 |
| ТНК | 109 | (13+14)/2=13,5 |
| МНИ | ||
| ВЦК | 107 | 15 |
| ДЖА | 106 | 16 |
| ВСИ | 105 | 17 |
| ЮЕР | 101 | 18 |
| ЖЕН | 97 | 19 |
| АНМ | 90 | 20 |
Шаг 3. Суммировать ранги значений в группе 7 «а» и в группе 7 «б»
Ранги 7 «а» = 1,5+3+4+9+9+12+13,5+13,5+17+20 = 102,5
Ранги 7 «б» = 1,5+5+6+7+9+11+15+16+18+19 = 107,5
Шаг 4. определить какая из ранговых сумм бОльшая.
Ранг 7 «а» ранговая сумма 7″б» больше
Шаг 5. Определить эмпирические значения критерия U Манна-Уитни по формуле:
,где — количество испытуемых в 1 группе; — количество испытуемых во 2 группе; — большая из двух ранговых сумм; — количество испытуемых в группе с бОльшей ранговой суммой.
Шаг 6. По таблице определить критические значения критерия U Манна-Уитни.
Шаг 7. Сравнить критические значения с эмпирическими.