что такое греческий парадокс
В свободное от отдыха время древнегреческие философы придумывали логические парадоксы
Многие из этих парадоксов уже давно решили и даже не один раз, но у кого-то подобные вещи могут вызвать приступ задумчивости. Попробуйте как-нибудь на досуге всерьёз поразмыслить хотя бы над одним из них и вы поймёте, как же тяжко было всем этим философам без современных знаний и технологий.
Летящая стрела
«Летящая стрела» или «Стрела Зенона» — одна из самых известных апорий, споры о которой продолжаются вот уже много веков и никакого явного и однозначного ответа на неё пока нет. Сама апория звучит так:
«Летящая стрела неподвижна, так как в каждый момент времени она занимает равное себе положение, то есть покоится; поскольку она покоится в каждый момент времени, то она покоится во все моменты времени, то есть не существует момента времени, в котором стрела совершает движение».
Ахиллес и черепаха
Ещё одна из апорий Зенона, основана на том утверждении, что Быстроногий Ахиллес никогда не догонит медленную черепаху, если в начале движения черепаха находится впереди. Звучит она так:
«Допустим, Ахиллес бежит в десять раз быстрее, чем черепаха, и находится позади неё на расстоянии в тысячу шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху».
Дихотомия
Очередная апория Зенона, утверждающая логическую противоречивость математической модели движения. Вот её текст:
«Чтобы преодолеть путь, нужно сначала преодолеть половину пути, а чтобы преодолеть половину пути, нужно сначала преодолеть половину половины, и так до бесконечности».
Парадокс лжеца
В научных кругах это утверждение ещё известно как «апория Евбулида». Её, в том или ином виде, наверняка, слышали практически все:
«То, что я утверждаю сейчас — ложно».
Если это высказывание истинно, получается, исходя из его содержания, верно то, что данное высказывание — ложь; но если оно — ложь, тогда неверно то, что оно утверждает, то есть утверждение о ложности данного высказывания неверно, значит, данное высказывание истинно. Таким образом, цепочка рассуждений возвращается в начало. Неразрывно с этой апорией связан и так называемый парадокс Пиноккио: Что будет, если Пиноккио скажет: «Сейчас у меня удлинится нос»? Если нос не увеличится — значит, Пиноккио соврал, и нос будет обязан тут же вырасти. А если нос вырастет — значит, он сказал правду, но тогда почему вырос нос?
Парадокс кучи
Этот логический парадокс также был сформулировал Евбулидом около IV века до н. э. Формулировка парадокса основана на той предпосылке, что одно зёрнышко ещё не образует кучи. И если мы будем прибавлять к нему каждый раз по одному зёрнышку, то не понятно в какой момент это множество станет кучей. Есть и негативная формулировка: «Если удалять из кучи в 1 млн зёрен по одному зёрнышку, с какого момента она перестаёт быть кучей?»
Лысый
По похожему принципу строится ещё одна апория Евбулида:
«Потеряв один волос, ещё не становишься лысым, потеряв два волоса — тоже; когда же начинается лысина?»
Корабль Тесея
Парадокс, который можно сформулировать так: «Если все составные части исходного объекта были заменены, остаётся ли объект тем же объектом?» Согласно греческому мифу, пересказанному Плутархом, корабль, на котором Тесей вернулся с Крита в Афины, хранился афинянами до эпохи Деметрия Фалерского, и ежегодно отправлялся со священным посольством на Делос. При починке в нём постепенно заменяли доски, до тех пор, пока среди философов не возник спор, тот ли это ещё корабль, или уже другой, новый? Кроме того, возникает вопрос: в случае постройки из старых досок второго корабля какой из них будет настоящим?
Парадокс всемогущества
Наиболее часто этот парадокс формулируют в виде вопроса: «Может ли Бог создать камень, который он сам не сможет поднять?» Парадоксальность заключается в том, что если ему это удастся, значит, его всемогущество утратило силу, а если нет, то он и не был всемогущ.
Софизм Эватла
Интересный логический парадокс древнегреческого происхождения. Этот парадокс иллюстрируется полулегендарным примером.
У древнегреческого софиста Протагора учился софистике и в том числе судебному красноречию некий Эватл. По заключенному между ними договору Эватл должен был заплатить за обучение 10 тысяч драхм только в том случае, если выиграет свой первый судебный процесс. В случае проигрыша первого судебного дела он вообще не был обязан платить.
Однако, закончив обучение, Эватл не стал участвовать в судебных тяжбах. Как следствие, он считал себя свободным от уплаты за учебу. Это длилось довольно долго, терпение Протагора иссякло, и он сам подал на своего ученика в суд. Таким образом, должен был состояться первый судебный процесс Эватла.
Протагор привёл следующую аргументацию: «Каким бы ни было решение суда, Эватл должен будет заплатить. Он либо выиграет свой первый процесс, либо проиграет. Если выиграет, то заплатит по договору, если проиграет, заплатит по решению суда».
Эватл возражал: «Ни в том, ни в другом случае я не должен платить. Если я выиграю, то я не должен платить по решению суда, если проиграю, то по договору».
Что такое греческий парадокс
Неожиданным импульсом к этой гипотезе стал парадокс Древней Греции. Греческое «чудо» — необычайный взлет научной мысли в I тысячелетии до нашей эры, занявший всего несколько столетий, поражает воображение одним уже тем, что в нем мы находим истоки почти всех современных наук.
Даже при самом поверхностном взгляде многое из того, что мы считаем сегодня новым, оказывается «хорошо забытым старым», и мы непременно обнаруживаем это, заглянув в античную Элладу.
Современные представления о строении материи на самом глубинном ее уровне очень близки по своей сути к теории Демокрита, датирующейся V веком до н. э.
Сегодняшние взгляды на бесконечность и дискретность пространства и времени были сформулированы Эпикуром в IV веке до н. э. Современник Эпикура Теофраст говорил о химической войне и химической взаимопомощи растений. Мы же поняли это лишь в 30-х годах XX века, после открытия фитонцидов. У Эмпедокла (V в. до н. э.) мы узнаем, что существовал раздельный генезис флоры и фауны, а учение Галена о происхождении человека от человекообразных обезьян на два тысячелетия предвосхитило Дарвина».
В чем же парадокс? В том, что волреки всякой логике самые глубокие и верные с точки зрения сегодняшней науки знания и теории принадлежат не позднеэллиноким мыслителям (Птолемей, Аристотель и др.), а их ранним предшественникам — Фалесу, Солону, Анаксагору, Гераклиту, Пифагору…
По мнению Юрия Каныгина, то, что именно они дали мощный импульс зарождению греческой науки, объясняется их приобщенностью к эзотерическим (тайным) знаниям, полученным ими в Древнем Египте, Персии, Вавилоне — государствах, интеллектуальный потенциал которых по сей день остается во многом загадочным.
Действительно, все свои открытия в астрономии и математике первый корифей греческой науки Фалес Милетский сделал после посещения Египта и Месопотамии. То же самое можно сказать о Демокрите, изучавшем астрономию у египетских жрецов и вавилонян, а медицину у индийских йогов. Гераклит, проведя несколько лет в Персии, первым сформулировал нам диалектическое миропонимание, сказав, что в основе всего — непрерывная борьба противоположностей, образующих высшее единство — гармонию мира. Что же касается загадочной даже для его современников фигуры Пифагора, принесшего грекам учение о числе как о скрытой сути вещей, то он не только объездил многие страны Востока, но, проведя 22 года в Египте, был принят в касту жрецов, пройдя для посвящения невероятные испытания воли.
Посвященные… Они возвращались из своих странствий с готовой доктриной, теорией, системой. Вполне возможно, что многие новые доктрины, мысли, концепции были созданы и развиты под влиянием эзотерических знаний. Глубину мысли древних начали постигать в XIX–XX веках.
3 удивительных древнегреческих парадокса
1. Дилемма крокодила является софизмом, то есть логическим парадоксом. Это означает ложное умозаключение, которое, тем не менее, при поверхностном рассмотрении кажется правильным. Софизм основан на преднамеренном, сознательном нарушении правил логики. Вот формулировка этого софизма:
— Твое несчастье растрогало меня, и я дам тебе шанс получить назад ребёнка. Угадай, отдам я его тебе или нет. Если ответишь правильно, я верну ребёнка. Если не угадаешь, я его не отдам.
Подумав, мать ответила:
— Ты не отдашь мне ребенка.
Если то, что я не отдам ребенка, — правда, я не отдам его, так как иначе сказанное не будет правдой. Если сказанное — неправда, значит, ты не угадала, и я не отдам ребенка по уговору.
Однако матери это рассуждение не показалось убедительным:
— Но ведь если я сказала правду, то ты отдашь мне ребенка, как мы и договорились. Если же я не угадала, что ты не отдашь ребенка, то ты должен мне его отдать, иначе сказанное мною не будет неправдой.
Другая формулировка этого парадокса:
Миссионер очутился у людоедов и попал как раз к обеду. Они разрешают ему выбрать, в каком виде его съедят. Для этого он должен произнести какое-нибудь высказывание с условием, что, если это высказывание окажется истинным, они его сварят, а если оно окажется ложным, его зажарят.
Что следует сказать миссионеру?
Разумеется, он должен сказать: «Вы зажарите меня». Если его действительно зажарят, окажется, что он высказал истину, и значит, его надо сварить. Если же его сварят, его высказывание будет ложным, и его следует как раз зажарить. Выхода у людоедов не будет: из «зажарить» вытекает «сварить», и наоборот.
2. Парадокс лжеца: «То, что я утверждаю сейчас — ложно», или «Данное высказывание — ложь».
То есть если правда, что данное высказывание ложь, то данное высказывание ложно. Если же ложно, что данное высказывание ложь, то данное высказывание правда. И цепочка рассуждений возвращается в начало.
Таким образом это высказывание противоречит «закону исключённого третьего» в двоичной логике.
Предложение такого рода принципиально не может быть ни доказано, ни опровергнуто в пределах того языка, на котором оно изложено.
3. Парадокс Эватла. У древнегреческого софиста Протагора учился софистике и в том числе судебному красноречию некий Эватл. По заключенному между ними договору Эватл должен был заплатить за обучение 10 тысяч драхм только в том случае, если выиграет свой первый судебный процесс. В случае проигрыша первого судебного дела он вообще не был обязан платить.
Однако, закончив обучение, Эватл не стал участвовать в судебных тяжбах. Как следствие, он считал себя свободным от уплаты за учебу. Это длилось довольно долго, терпение Протагора иссякло, и он сам подал на своего ученика в суд. Таким образом, должен был состояться первый судебный процесс Эватла.
Протагор привёл следующую аргументацию: «Каким бы ни было решение суда, Эватл должен будет заплатить. Он либо выиграет свой первый процесс, либо проиграет. Если выиграет, то заплатит по договору, если проиграет, заплатит по решению суда».
Эватл возражал: «Ни в том, ни в другом случае я не должен платить. Если я выиграю, то я не должен платить по решению суда, если проиграю, то по договору».
Протагор, по не вполне надёжным сведениям, посвятил этому случаю несохранившееся сочинение «Тяжба о плате».
3 удивительных древнегреческих парадокса
— Твое несчастье растрогало меня, и я дам тебе шанс получить назад ребёнка. Угадай, отдам я его тебе или нет. Если ответишь правильно, я верну ребёнка. Если не угадаешь, я его не отдам.
Подумав, мать ответила:
— Ты не отдашь мне ребенка.
Если то, что я не отдам ребенка, — правда, я не отдам его, так как иначе сказанное не будет правдой. Если сказанное — неправда, значит, ты не угадала, и я не отдам ребенка по уговору.
Однако матери это рассуждение не показалось убедительным:
— Но ведь если я сказала правду, то ты отдашь мне ребенка, как мы и договорились. Если же я не угадала, что ты не отдашь ребенка, то ты должен мне его отдать, иначе сказанное мною не будет неправдой.
Другая формулировка этого парадокса:
Миссионер очутился у людоедов и попал как раз к обеду. Они разрешают ему выбрать, в каком виде его съедят. Для этого он должен произнести какое-нибудь высказывание с условием, что, если это высказывание окажется истинным, они его сварят, а если оно окажется ложным, его зажарят.
Что следует сказать миссионеру?
Разумеется, он должен сказать: «Вы зажарите меня». Если его действительно зажарят, окажется, что он высказал истину, и значит, его надо сварить. Если же его сварят, его высказывание будет ложным, и его следует как раз зажарить. Выхода у людоедов не будет: из «зажарить» вытекает «сварить», и наоборот.
То есть если правда, что данное высказывание ложь, то данное высказывание ложно. Если же ложно, что данное высказывание ложь, то данное высказывание правда. И цепочка рассуждений возвращается в начало.
Таким образом это высказывание противоречит «закону исключённого третьего» в двоичной логике.
Предложение такого рода принципиально не может быть ни доказано, ни опровергнуто в пределах того языка, на котором оно изложено.
Однако, закончив обучение, Эватл не стал участвовать в судебных тяжбах. Как следствие, он считал себя свободным от уплаты за учебу. Это длилось довольно долго, терпение Протагора иссякло, и он сам подал на своего ученика в суд. Таким образом, должен был состояться первый судебный процесс Эватла.
Протагор привёл следующую аргументацию: «Каким бы ни было решение суда, Эватл должен будет заплатить. Он либо выиграет свой первый процесс, либо проиграет. Если выиграет, то заплатит по договору, если проиграет, заплатит по решению суда».
Эватл возражал: «Ни в том, ни в другом случае я не должен платить. Если я выиграю, то я не должен платить по решению суда, если проиграю, то по договору».
Протагор, по не вполне надёжным сведениям, посвятил этому случаю несохранившееся сочинение «Тяжба о плате».
19 знаменитых парадоксов, которые могут оставить вас в замешательстве
Будьте готовы: придется много думать.
«Я знаю, что ничего не знаю», — однажды сказал древнегреческий философ Сократ и был прав. Даже в таких точных науках, как математика, физика или логика, есть задачи, решить которые не под силу лучшим умам человечества. Такие нерешаемые задачи называют парадоксами — тем, что противоречит здравому смыслу.
Ниже мы собрали 19 известных парадоксов, о которых вы еще долго не сможете забыть.
1. Проблема Молинье
Этот мысленный философский эксперимент был сформулирован еще в 1689 году, и звучит он так:
«Представьте, что слепой с рождения человек, который научился распознавать предметы (например, куб и шар) через прикосновения, вдруг прозрел. Сможет ли он одним лишь взглядом понять, что есть шар, а что — куб?
Ответ на этот вопрос мог бы разрешить одну из загадок человеческой природы: обладаем ли мы способностью сопоставлять объект, который мы потрогали, с тем, что мы увидели.
2. Вопрос от математика Рэймонда Джонсона
«Если вы выберете ответ случайным образом, какова вероятность, что он будет правильным?»
Разве это не сбивает с толку?
3. Логический парадокс из Греции
Что должна сделать мать? Это условие по умолчанию невыполнимо с точки зрения логики.
4. Парадокс телепортации от Дерека Парфита
Представьте, что вы входите в телепорт, чтобы отправиться на Марс, — устройство создает точную копию всех ваших атомов на Красной планете. Вместе с этим оно разрушает ваше настоящее (исходное) тело. Получившаяся копия — организм, который выглядит точно так же, как вы, и даже обладает вашим сознанием. Что получается в результате: вы выживаете или все-таки умираете?
5. Парадокс лжеца
Его сформулировал критянин Эпименид. Если мужчина заявит: «Я всегда лгу» — каким будет его утверждение: верным или ложным?
6. Проблема Геттиера
«Корова на лугу» — один из классических примеров проблемы, описанной философом Эдмундом Геттиером.
Фермер с плохим зрением встречает молочника и делится с ним своими переживаниями о том, что его корова ушла с фермы. Молочник уверяет фермера, что не стоит волноваться: он видел корову на лугу неподалеку. Фермер смотрит в указанном направлении и видит что-то крупное, с черными и белыми пятнами.
Он удовлетворен увиденным и считает, что знает, где его корова. Чуть позже фермер решает пойти на луг, чтобы еще раз проверить, что корова действительно там. Он видит, что корова на самом деле на лугу, но, к его удивлению, ее не видно за деревьями.
И тут он замечает на ветвях дерева огромный черно-белый лист бумаги. Фермер понимает, что молочник по ошибке принял этот лист за корову. Вопрос: был ли прав молочник, когда сказал, будто знает, что корова на лугу?
7. Парадокс бережливости Джона Робертсона
Представим ситуацию: экономика находится в упадке. Кажется, что единственный способ исправить ситуацию — начать экономить. Но возникает другая проблема: если все начнут экономить, снизится общий спрос, что приведет к уменьшению наших доходов. Результат — ухудшение экономики. Так что же нам делать?
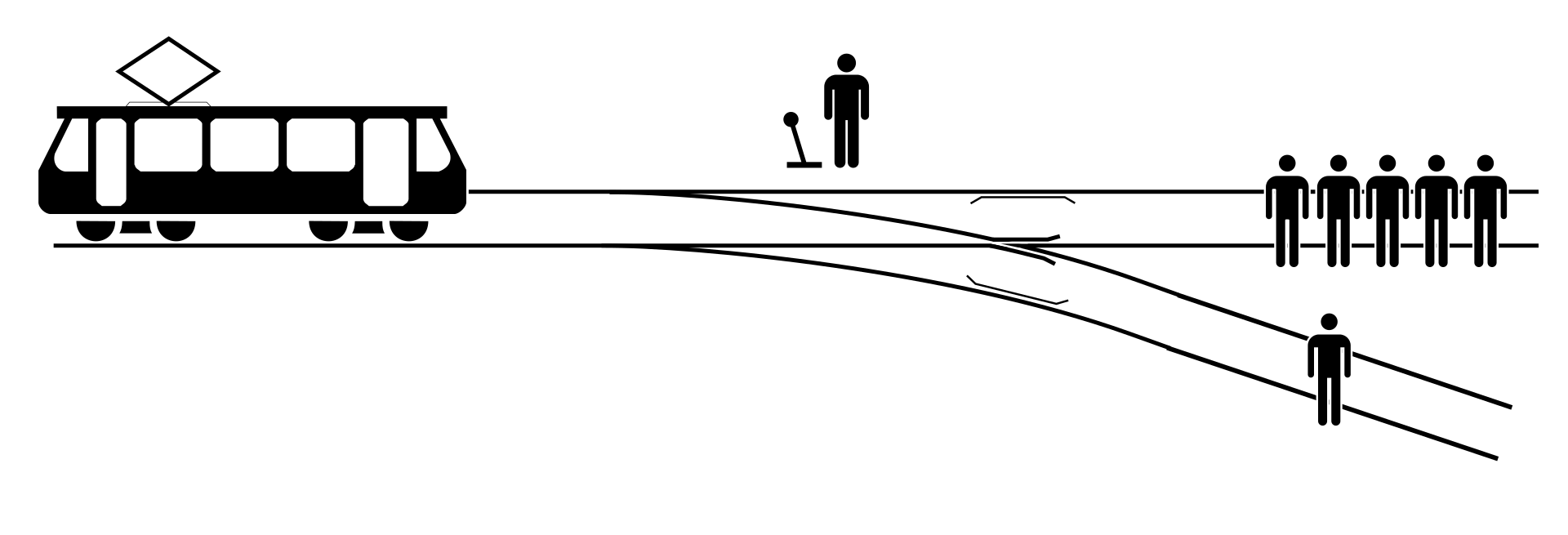
8. Проблема вагонетки философа Филиппы Фут
Вы стоите на краю рельсов и видите приближающийся поезд. На путях стоят еще пять человек, и если ничего не сделать — их переедет поезд. К счастью, прямо перед вами есть кнопка, и если вы нажмете на нее, поезд изменит направление и сойдет на другие пути. Однако на других путях стоит человек, и если нажать кнопку — он погибнет. Что вы должны сделать? Пожертвовать одним, но спасти пятерых, или наоборот?
9. Парадокс лестницы (шеста) в специальной теории относительности
Согласно специальной теории относительности, объекты, движущиеся с околосветовой скоростью, становятся короче.
Представим лестницу, которую вносят в гараж в переднюю дверь и сразу же выносят через заднюю. Длина лестницы на несколько метров больше длины гаража, поэтому ее нельзя хранить в закрытом помещении. Допустим, что лестница движется с околосветовой скоростью по той же траектории, по которой ее вносят в гараж.
За счет лоренцева сжатия длина лестницы относительно гаража должна уменьшиться, поэтому при соответствующей скорости лестница может полностью уместиться в помещении. В этот момент обе двери гаража можно быстро закрыть (чтобы лестница в нем уместилась), а затем открыть (чтобы лестница не ударилась в заднюю дверь гаража).
С другой стороны, если рассмотреть ситуацию из системы отсчета лестницы, то ее длина остается прежней, а длина гаража, напротив, сокращается. Следовательно, в этой ситуации лестница не может полностью уместиться в закрытом гараже. Поскольку обе системы отсчета равноправны, получается парадокс.
10. Проблема свободы Лукреция
Если атомы в нашем мозгу всегда движутся предсказуемым образом, можем ли мы говорить о свободе воли?
Представьте: вы путешественник во времени, который перемещается в период жизни Бетховена и передает молодому композитору черновики сонаты. Бетховен представляет публике музыкальное произведение. Кто в таком случае автор композиции?
12. Парадокс Зенона Элейского
Зенон Элейский сформулировал несколько парадоксальных рассуждений на тему движения, которые служат предметом дискуссий более двух тысячелетий! Одно из них — «Летящая стрела».
Летящая стрела неподвижна, так как в каждый момент она покоится, а поскольку она покоится в каждый момент времени, то она покоится всегда.
13. Дилемма математика Архита
ЕКА и Planck Collaboration
Он сформулировал ее еще в V веке до нашей эры.
Если я подойду к краю Вселенной и протяну руку, выйдет ли рука за ее пределы?
Примечательно, что этот древний вопрос порождает дискуссии современных ученых: если Вселенная расширяется, то куда? Если она расширяется в пустоту (небытие), не должно ли это пространство быть частью Вселенной? А если мы выйдем за пределы Вселенной, как далеко будет ее конец?
14. Парадокс «Протагор и Эватл»
У софиста Протагора был ученик Эватл, который брал у него уроки политического и судебного красноречия. Они договорились: Эватл заплатит Протагору за обучение только в том случае, если он выиграет свое первое судебное дело. Но после обучения Эватл не стал участвовать ни в одном процессе, соответственно, денег он не заплатил.
Протагор подал на Эватла в суд, чтобы получить свой заслуженный гонорар. Он пригрозил: «Если тебя присудят к уплате, ты должен будешь заплатить по приговору суда; если же тебя не присудят к уплате, то ты, как выигравший свой первый судебный процесс, должен будешь заплатить по нашему уговору».
На что Эватл ответил: «Все правильно: меня или присудят к уплате гонорара, или не присудят; если меня присудят к уплате, то я, как проигравший свой первый судебный процесс, не заплачу по нашему уговору; если же меня не присудят к уплате, то я не заплачу по приговору суда».
15. Вопрос персидского философа Авиценны
Представьте себе человека, который полностью лишен чувств. Он не может видеть, слышать и ощущать вкус. У него отсутствует обоняние и осязание. Понимает ли он, что он вообще живет? Авиценна отвечает на этот вопрос утвердительно и делает вывод о существовании души. А как бы ответили вы?
16. Проблема философа Фрэнка Джексона
Мэри — талантливый ученый, которая знает о цветах все. Она знает о том, как возникают цвета и как их обрабатывает мозг человека. Однако Мэри никогда не видела красок. Если она выйдет из своей черно-белой комнаты и включит цветной телевизор, сможет ли она что-нибудь узнать?
17. Парадокс Ольберса
В бесконечной Вселенной все пространство заполнено звездами, и всякий луч зрения должен заканчиваться на звезде — совсем как в густом лесу, когда нас окружает «стена» из деревьев, расположенных вдали. Тогда почему небо ночью такое темное? Бесконечное количество звезд означает, что небосвод должен сиять. Итак, как мы можем объяснить ночную темноту?
18. Самоубийство Роналда Опуса
Так что же это: убийство или самоубийство?
19. Корабль Тесея
Согласно греческому мифу, корабль, на котором Тесей вернулся с Крита в Афины, бережно хранился афинянами. Они заботились о судне и с течением времени одну за другой меняли износившиеся детали. В результате от оригинальных «запчастей» корабля не осталось и следа. Главный вопрос: перед нами все еще корабль Тесея или новое судно?