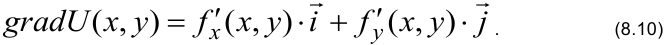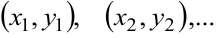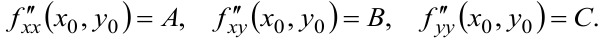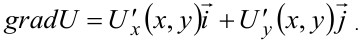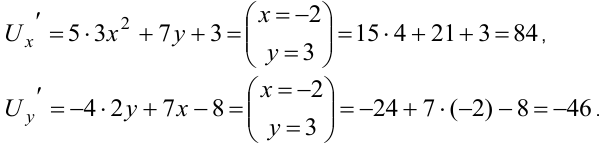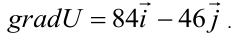что такое градиент в математике простыми словами
Значение слова «градиент»
[От лат. gradiens, gradientis — шагающий]
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
, значение которой меняется от одной точки пространства к другой (скалярного поля), а по величине (модулю) равный скорости роста этой величины в этом направлении.
Например, если взять в качестве
высоту поверхности земли над уровнем моря, то её градиент в каждой точке поверхности будет показывать «направление самого крутого подъёма», и своей величиной характеризовать крутизну склона.
С математической точки зрения на градиент можно смотреть как на:
1. Коэффициент линейности изменения значения функции многих переменных от изменения значения аргумента
2. Вектор в пространстве области определения скалярной функции многих переменных, составленный из частных производных
3. Строки Матрицы Якоби содержат градиенты составных скалярных функций из которых состоит векторная функция многих переменных
Пространство, на котором определена функция и её градиент, может быть, вообще говоря, как обычным трёхмерным пространством, так и пространством любой другой размерности любой физической природы или чисто абстрактным (безразмерным).
Термин впервые появился в метеорологии, а в математику был введён Максвеллом в 1873 г. Обозначение grad тоже предложил Максвелл.
Градиент и его свойства
Градиентом функции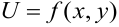 
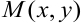
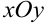
в данной точке 
называется вектор, расположенный в плоскости 
с началом в точке
Основное свойство градиента: направление градиента функции в точке является направлением быстрейшего возрастания функции, его модуль равен наибольшей скорости возрастания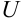 
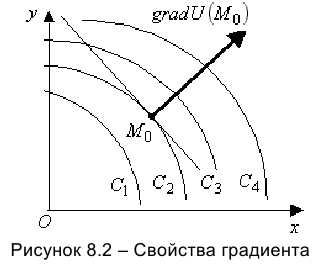
в заданной точке.
Другое свойство градиента: он перпендикулярен касательной линии уровня, проходящей через точку начала градиента.
Иллюстрация свойств градиента — на рисунке 8.2. Показаны линии уровня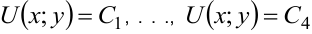 
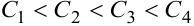
, причем 
.
Через точку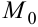 
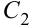
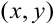
, лежащую на линии с уровнем 
проведены касательная и градиент, которые перпендикулярны друг другу. Градиент направлен в сторону возрастания функции 
.
8.6 Экстремум функции двух переменных. Необходимые и достаточные условия экстремума
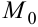
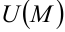
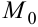
Точка называется точкой максимума функции 
, если значение функции в этой точке больше, чем её значение в любой другой точке некоторой (хотя бы малой) окрестности точки . Аналогично (с заменой «больше» на «меньше») определяется точка минимума функции.
Точки минимума и максимума объединяются под общим названием точки экстремума.
Для функции двух переменных точка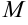 
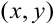
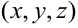
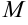
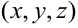
имеет две координаты для функции трёх переменных — три координаты 
. При этом окрестностью точки является открытый шар с центром в этой точке.
Поиск критических точек, т.е. точек в которых может быть экстремум функции 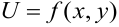, производится при помощи необходимого условия экстремума:
Решение системы (8.12) определяет координаты критических точек 
Однако необходимого условия мало для существования точек экстремума.
Нужно провести исследование критических точек с использованием достаточных условий экстремума.
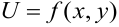
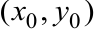
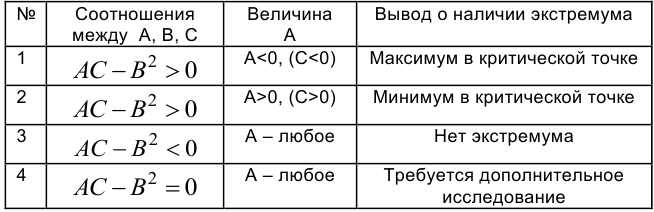
Для функции двух переменных введём обозначения для вторых частных производных в критической точке 
:
Достаточные условия приводим в таблице 4.
Таблица 4 — Достаточные условия экстремума функции двух переменных
Пример:
Дана функция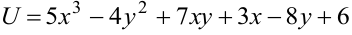 
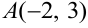
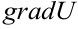
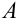
и точка 
. Найти градиент функции 
в заданной точке 
.
Решение:
Используем формулу градиента
Определяем частные производные и вычисляем их при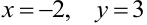 
.
При вычислении частной производной по одной из переменных вторая переменная считается постоянной величиной.
Значения частных производных подставляем в формулу градиента:
Ответ: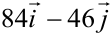 
.
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
СОДЕРЖАНИЕ
Мотивация
Обозначение
Определение
Когда функция также зависит от параметра, такого как время, градиент часто относится просто к вектору только его пространственных производных (см. Пространственный градиент ).
Декартовы координаты
В трехмерной декартовой системе координат с евклидовой метрикой градиент, если он существует, задается следующим образом:
Цилиндрические и сферические координаты
В цилиндрических координатах с евклидовой метрикой градиент задается следующим образом:
В сферических координатах градиент определяется как:
Общие координаты
Последнее выражение соответствует приведенным выше выражениям для цилиндрических и сферических координат.
Связь с производной
Связь с полной производной
С вычислительной точки зрения, учитывая касательный вектор, вектор можно умножить на производную (в виде матриц), что равносильно взятию скалярного произведения с градиентом:
( d ж п ) ( v ) знак равно [ ∂ ж ∂ Икс 1 ( п ) ⋯ ∂ ж ∂ Икс п ( п ) ] [ v 1 ⋮ v п ] знак равно ∑ я знак равно 1 п ∂ ж ∂ Икс я ( п ) v я знак равно [ ∂ ж ∂ Икс 1 ( п ) ⋮ ∂ ж ∂ Икс п ( п ) ] ⋅ [ v 1 ⋮ v п ] знак равно ∇ ж ( п ) ⋅ v <\ Displaystyle (df_
) (v) = <\ begin 
Дифференциальная или (внешняя) производная
Наилучшее линейное приближение дифференцируемой функции
Градиент связан с дифференциалом формулой
Если R n рассматривается как пространство векторов-столбцов (размерности n ) (действительных чисел), то можно рассматривать df как вектор-строку с компонентами
Линейное приближение к функции
Связь с производной Фреше
Как следствие, обычные свойства производной сохраняются для градиента, хотя градиент сам по себе не является производной, а скорее двойственен производной:
Другие свойства и применения
Наборы уровней
В более общем смысле, любая вложенная гиперповерхность в римановом многообразии может быть вырезана уравнением вида F ( P ) = 0 таким, что dF нигде не равно нулю. Тогда градиент F нормален к гиперповерхности.
Консервативные векторные поля и градиентная теорема
Градиент функции называется градиентным полем. (Непрерывное) поле градиента всегда является консервативным векторным полем : его линейный интеграл вдоль любого пути зависит только от конечных точек пути и может быть вычислен с помощью градиентной теоремы (основная теорема исчисления для линейных интегралов). И наоборот, (непрерывное) консервативное векторное поле всегда является градиентом функции.
Обобщения
Якобиан
Градиент векторного поля
Поскольку полная производная векторного поля является линейным отображением векторов в векторы, это тензорная величина.
(где используется обозначение суммирования Эйнштейна, а тензорное произведение векторов e i и e k является диадическим тензором типа (2,0)). В целом это выражение равно транспонированной матрице Якоби:
В криволинейных координатах или, в более общем смысле, на изогнутом многообразии градиент включает символы Кристоффеля :
Выражаясь более инвариантно, градиент векторного поля f может быть определен связностью Леви-Чивиты и метрическим тензором:
Римановы многообразия
где X j обозначает j- й компонент X в этой координатной карте.
Итак, локальная форма градиента принимает вид:
Градиент (математика)
Другими словами, градиент — это производная по пространству, но в отличие от производной по одномерному времени, градиент является не скаляром, а векторной величиной.
С математической точки зрения на градиент можно смотреть как на:
Пространство, на котором определена функция и её градиент, может быть, вообще говоря, как обычным трёхмерным пространством, так и пространством любой другой размерности любой физической природы или чисто абстрактным (безразмерным).
Содержание
Ознакомление [ | ]
Пусть температура в комнате задана с помощью скалярного поля T таким образом, что в каждой точке, заданной координатами (x, y, z) температура равняется T(x, y, z) (предположим, что температура не изменяется с течением времени). В каждой точке комнаты градиент функции T будет показывать направление, в котором температура возрастает быстрее всего. Величина градиента определяет, насколько быстро температура возрастает в данном направлении.
Определение [ | ]
d f = ∑ i ( ∂ i f ) d x i <\displaystyle df=\sum _(\partial _f)\,dx^>
или, опуская по правилу Эйнштейна знак суммы,
(в ортонормированном базисе мы можем писать все индексы нижними, как мы и делали выше). Однако градиент оказывается настоящим ковариантным вектором в любых криволинейных координатах.
Используя интегральную теорему
∭ V ∇ φ d V = ∬ S φ d s <\displaystyle \iiint \limits _\varphi \,d\mathbf > ,
градиент можно выразить в интегральной форме:
Пример [ | ]
В физике [ | ]
В различных отраслях физики используется понятие градиента различных физических полей.
В естественных науках [ | ]
Понятие градиента находит применение не только в физике, но и в смежных и даже сравнительно далёких от физики науках (иногда это применение носит количественный, а иногда и просто качественный характер).
Например, градиент концентрации — нарастание или уменьшение по какому-либо направлению концентрации растворённого вещества, градиент температуры — увеличение или уменьшение по какому-то направлению температуры среды и т. д.
Градиент таких величин может быть вызван различными причинами, например, механическим препятствием, действием электромагнитных, гравитационных или других полей или различием в растворяющей способности граничащих фаз.
В экономике [ | ]
В экономической теории понятие градиента используется для обоснования некоторых выводов. В частности, используемые для нахождения оптимума потребителя метод множителей Лагранжа и условия Куна-Таккера (позаимствованные из естественных наук) основаны на сопоставлении градиентов функции полезности и функции бюджетного ограничения.
Геометрический смысл [ | ]
Связь с производной по направлению [ | ]
Таким образом, для вычисления производной скалярной функции векторного аргумента по любому направлению достаточно знать градиент функции, то есть вектор, компоненты которого являются её частными производными.
Градиент в ортогональных криволинейных координатах [ | ]
Полярные координаты (на плоскости) [ | ]
Цилиндрические координаты [ | ]
Сферические координаты [ | ]
Градиенты: большой обзор
Рассказываем, какие бывают градиенты, как их создавать и как готовить к печати.
Градиенты используются в графическом, интерфейсном и информационном дизайне. Однако они не так просты, как хотелось бы: сложности могут возникнуть уже на этапе создания самого простого градиента и не закончиться даже при выводе на печать. Отдельная боль — столь модные сегодня mesh-градиенты. В этой статье мы расскажем всё, что вы должны знать о градиентах и работе с ними.
Из статьи вы узнаете:
Ведущий интерфейсный дизайнер в K&K TEAM, увлечён дизайном, технологиями и людьми. В свободное время ведёт Telegram-канал «Karoza Ҩ».
Цветовые градиенты
В графическом дизайне и искусстве градиенты используют для мягкого сочетания нескольких цветов или же в создании выразительных абстракций для рекламы или упаковки. Например, художник Филипе Пантоне использует экспрессивные градиенты в большинстве своих произведений. А приложение Instagram для своего логотипа выбрало сложный четырёхцветный градиент.
В интерфейсном дизайне у градиентов тоже множество применений: от чисто технических, когда нужно локально затемнить фон под текстом для лучшей читаемости, до декоративных — они делают дизайн более живым, помогают расставить акценты, привлечь внимание к наиболее важным блокам в интерфейсе.
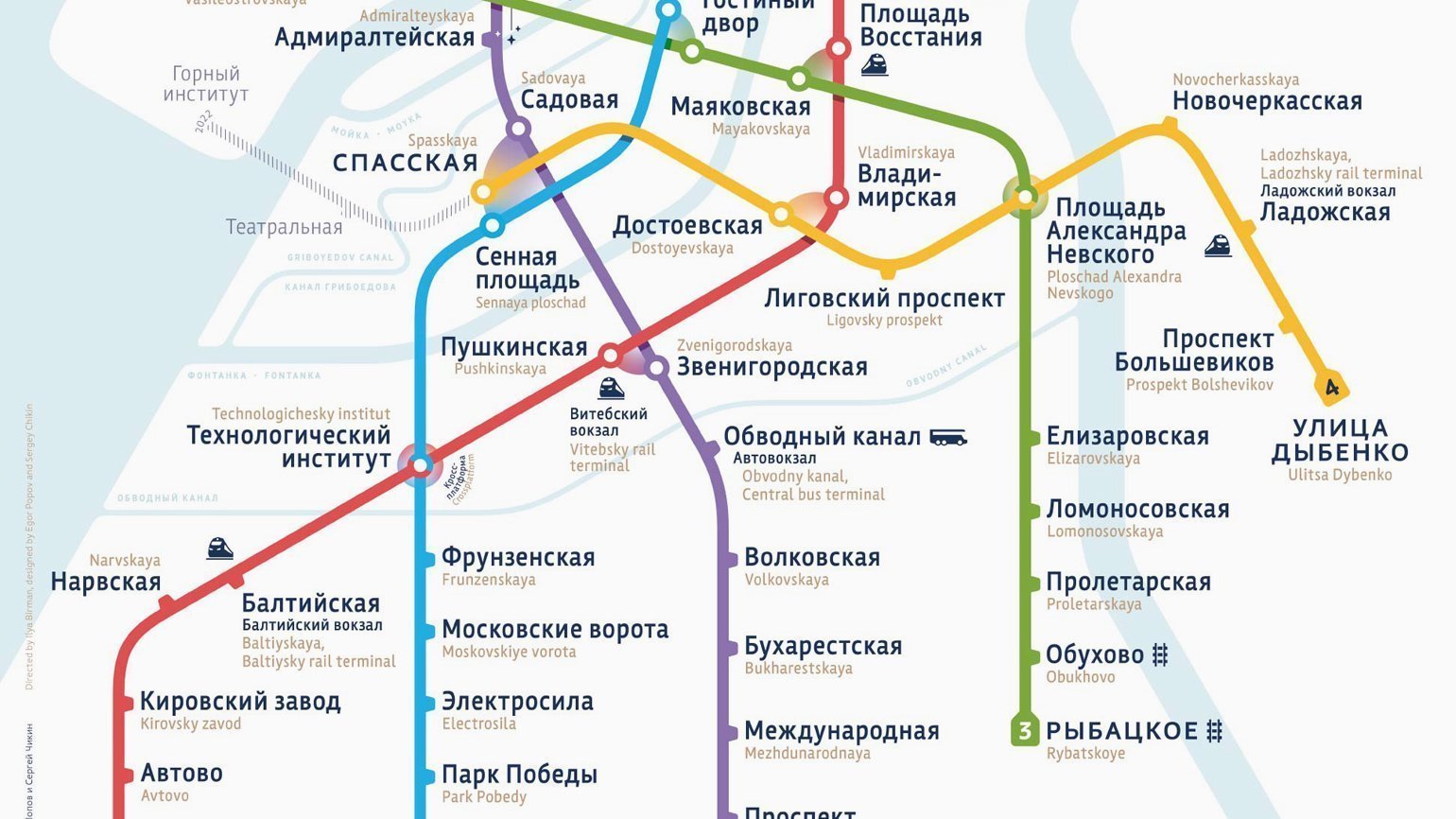
Один из интересных приёмов использования градиентов можно увидеть на схеме санкт-петербургского метро, предложенной Ильёй Бирманом. Линии, которые соединяют переходы с одной станции на другую, на карте соединяются плавным переходом цвета при помощи градиента.
Создание градиентов
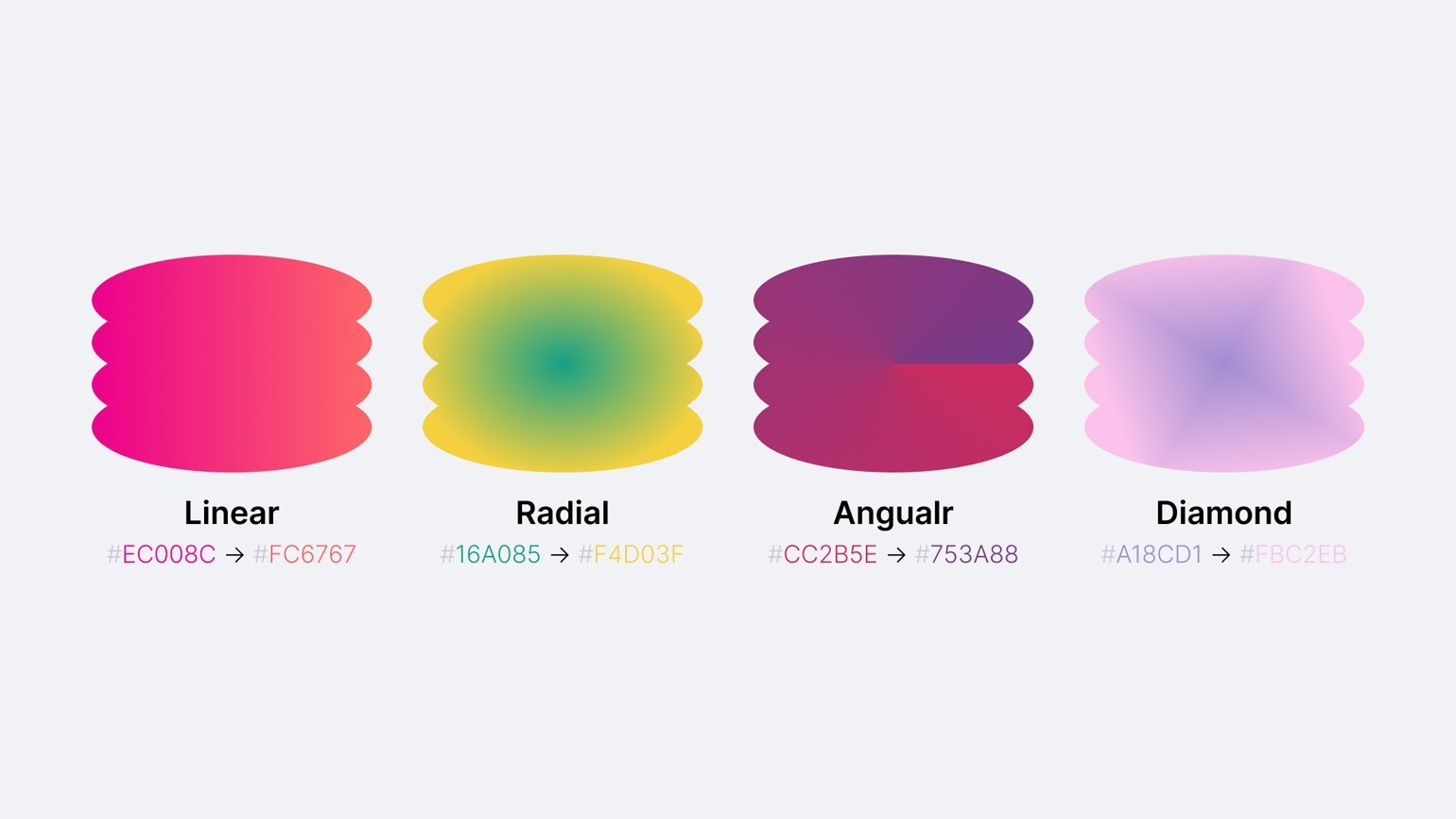
Технически создание простого градиента не составляет труда, достаточно выбрать цвета для перехода, направление и тип градиента: Linear (линейный), Radial (круговой, радиальный), Angular (угловой, конусный), Diamond (ромбовидный, алмазный).
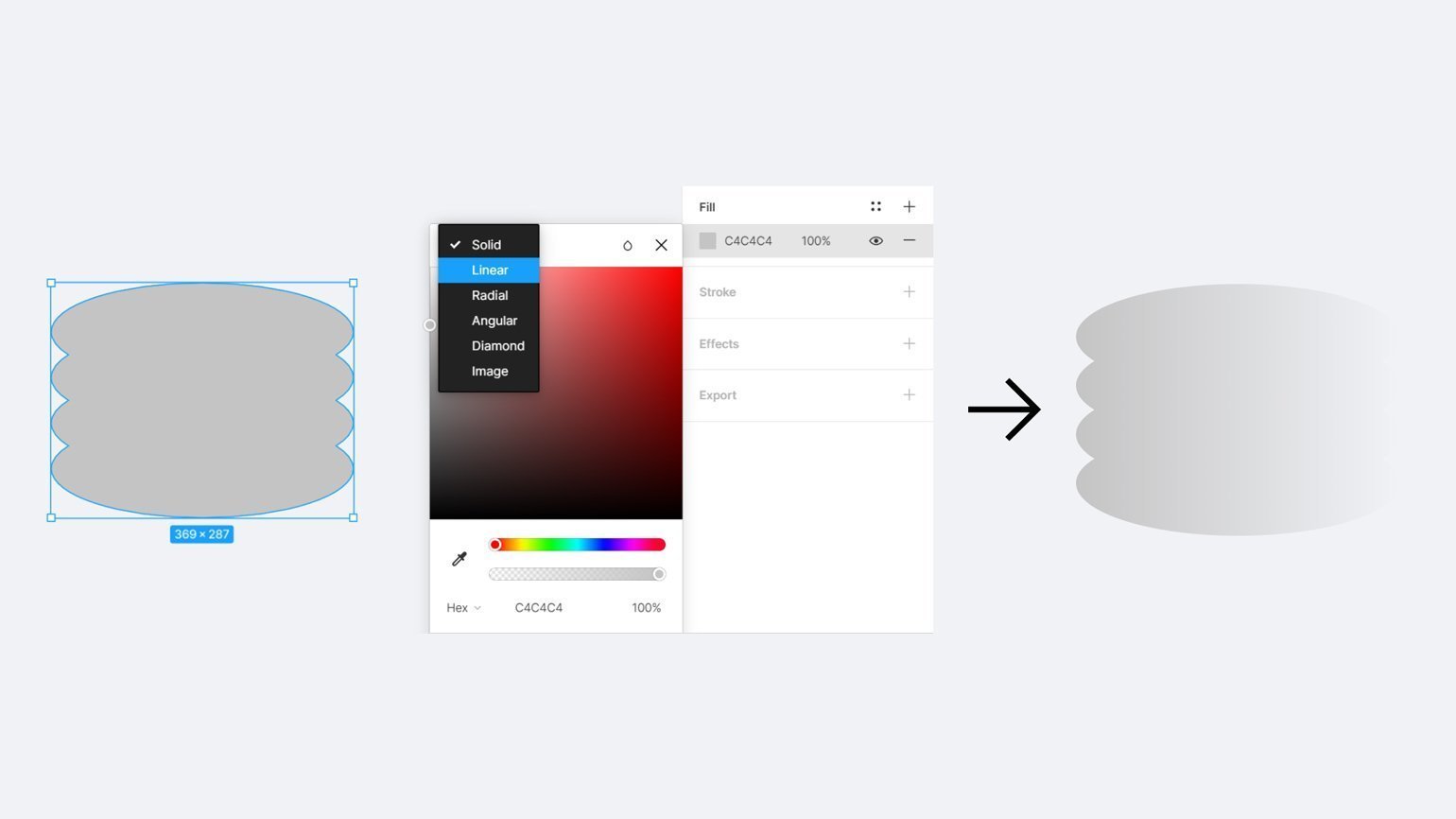
В Figma для создания градиента нужно выделить фигуру, затем в свойстве Fill выбрать тип градиента.
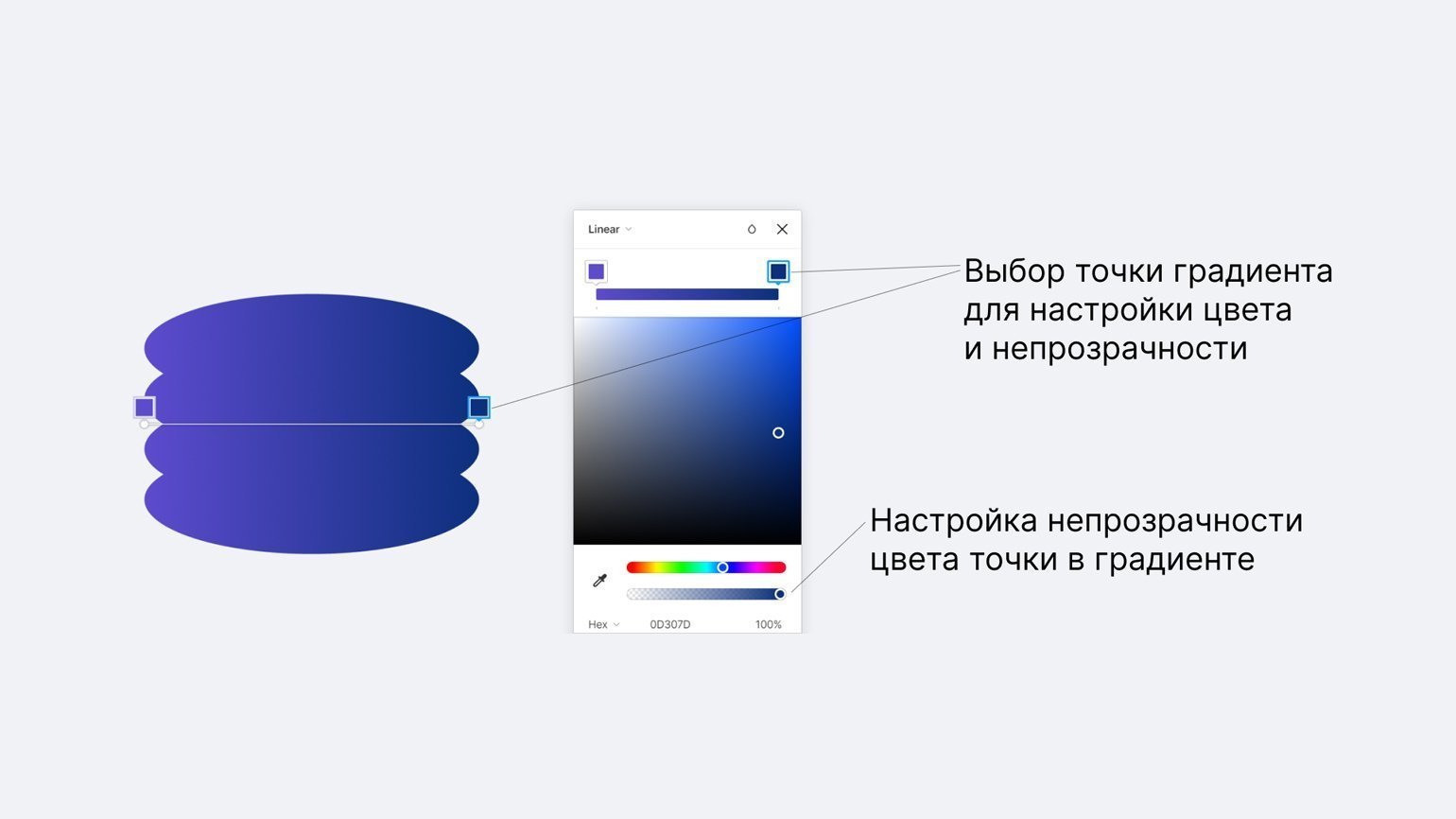
Для настройки цветов выделите точку градиента и укажите её цвет и непрозрачность.
Чтобы задать направление градиента, надо выделить точку на конце отрезка градиента и передвинуть её. Если в этот момент удерживать клавишу Shift, направление градиента будет кратно 45°.
Если надо добавить ещё один цвет в градиент, то надо кликнуть по линии между двумя цветами в нужном месте. Для удаления цвета кликните по точке и нажмите Delete на клавиатуре.
Точки градиента можно передвигать до достижения нужного результата.
С помощью этих простых манипуляций получаются сложные и красивые градиенты из множества цветов с плавными переходами. Однако создать гармоничный градиент с первого раза может быть сложновато, поэтому иногда проще выбрать из готовых.
Выбор градиентов
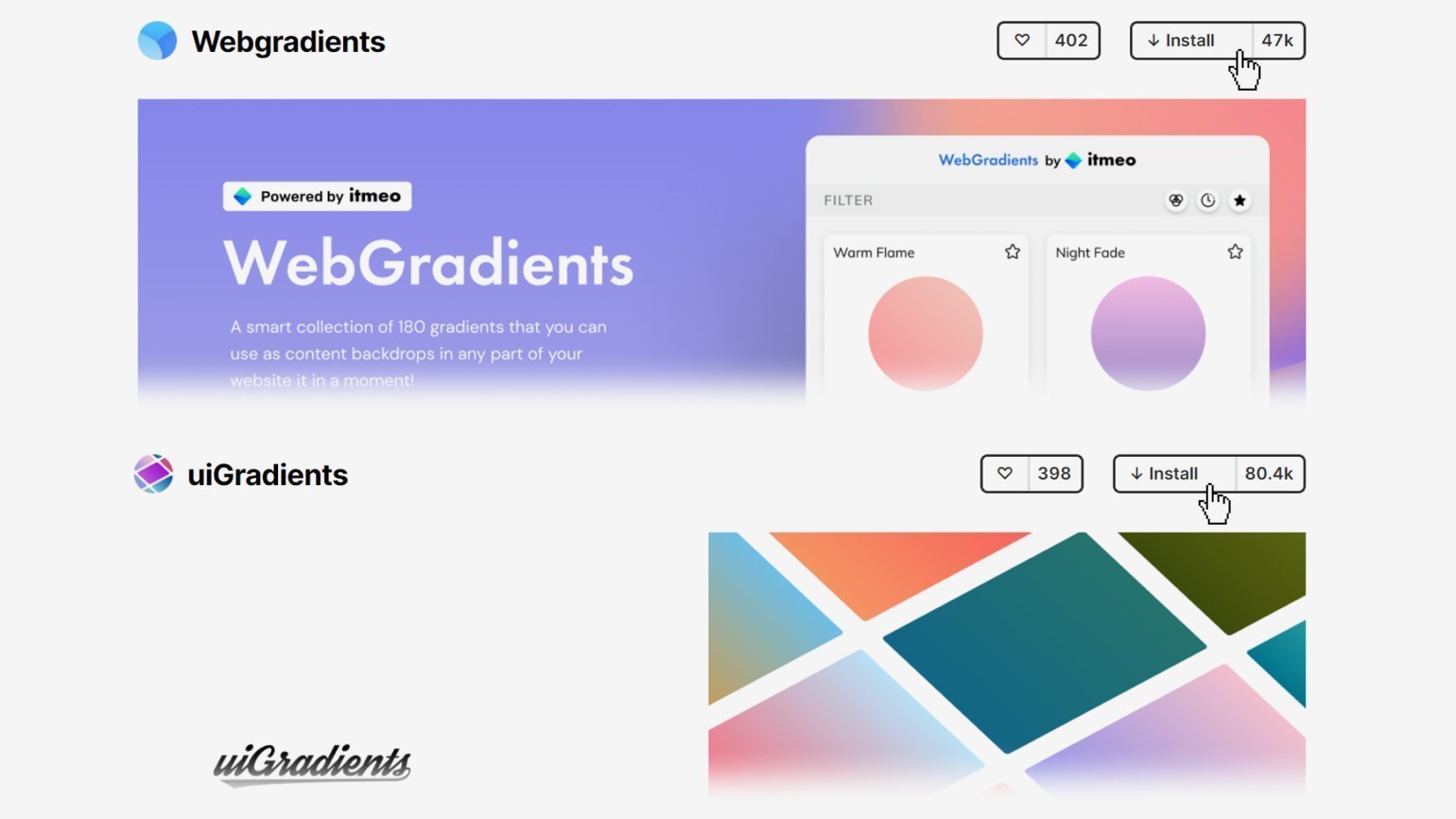
В Figma для работы с градиентами используют плагины Webgradients и uiGradients.
Первым делом нужно установить плагины в Figma Community, для этого на странице плагина нажмите на кнопку Install в правом верхнем углу.
После установки вернитесь в свой проект, выделите любую фигуру, а затем запустите плагин.
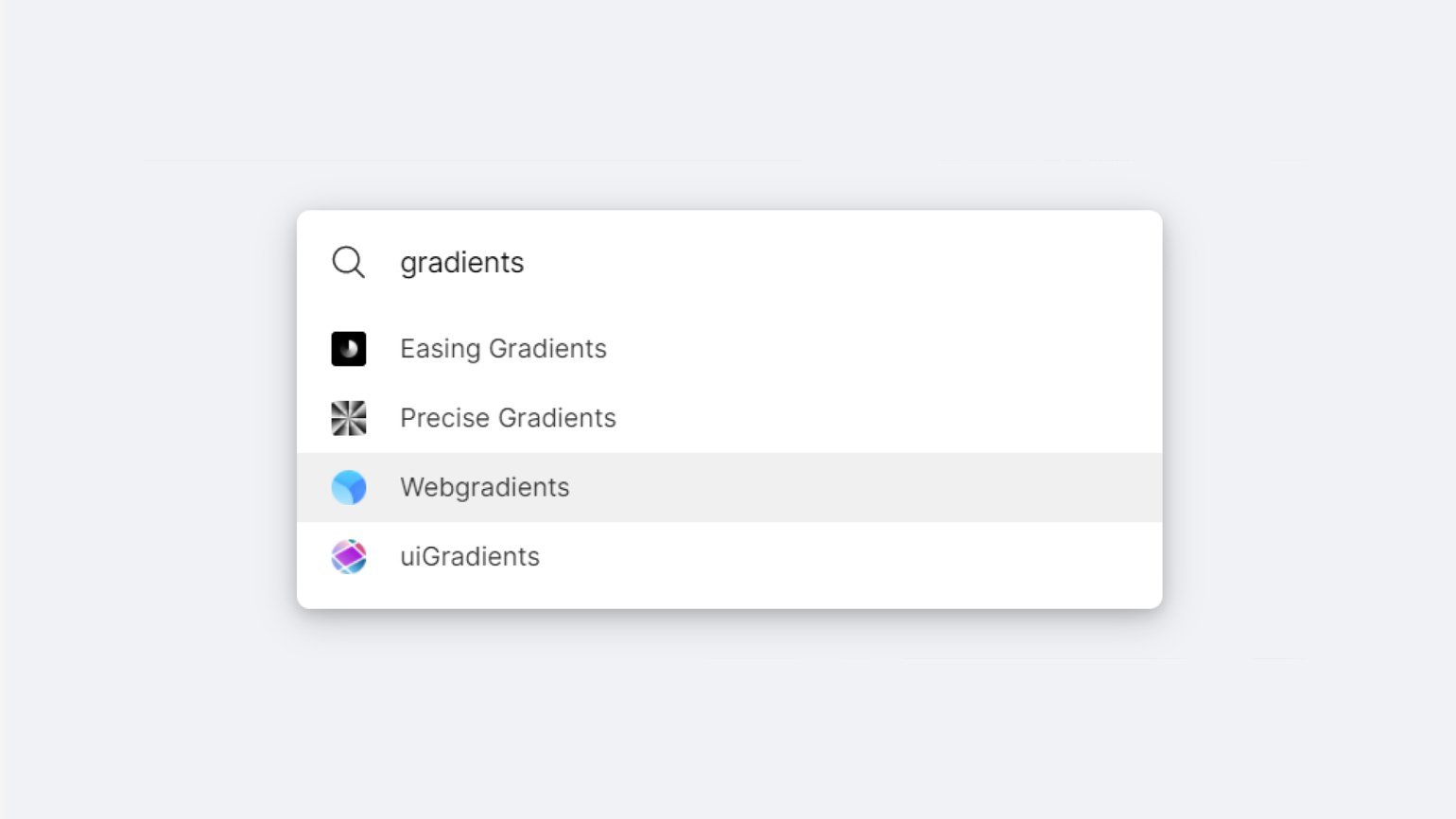
Выбрать его можно через поиск, для этого нажмите клавиши Ctrl (⌘) и «/» одновременно, начните вводить название плагина и выберите нужный, кликнув по его названию. Либо можно нажать правую кнопку мыши на объекте, выбрать в открывшемся меню Plugins и кликнуть по названию плагина в появившемся списке. Первый вариант удобнее, если плагинов установлено много.
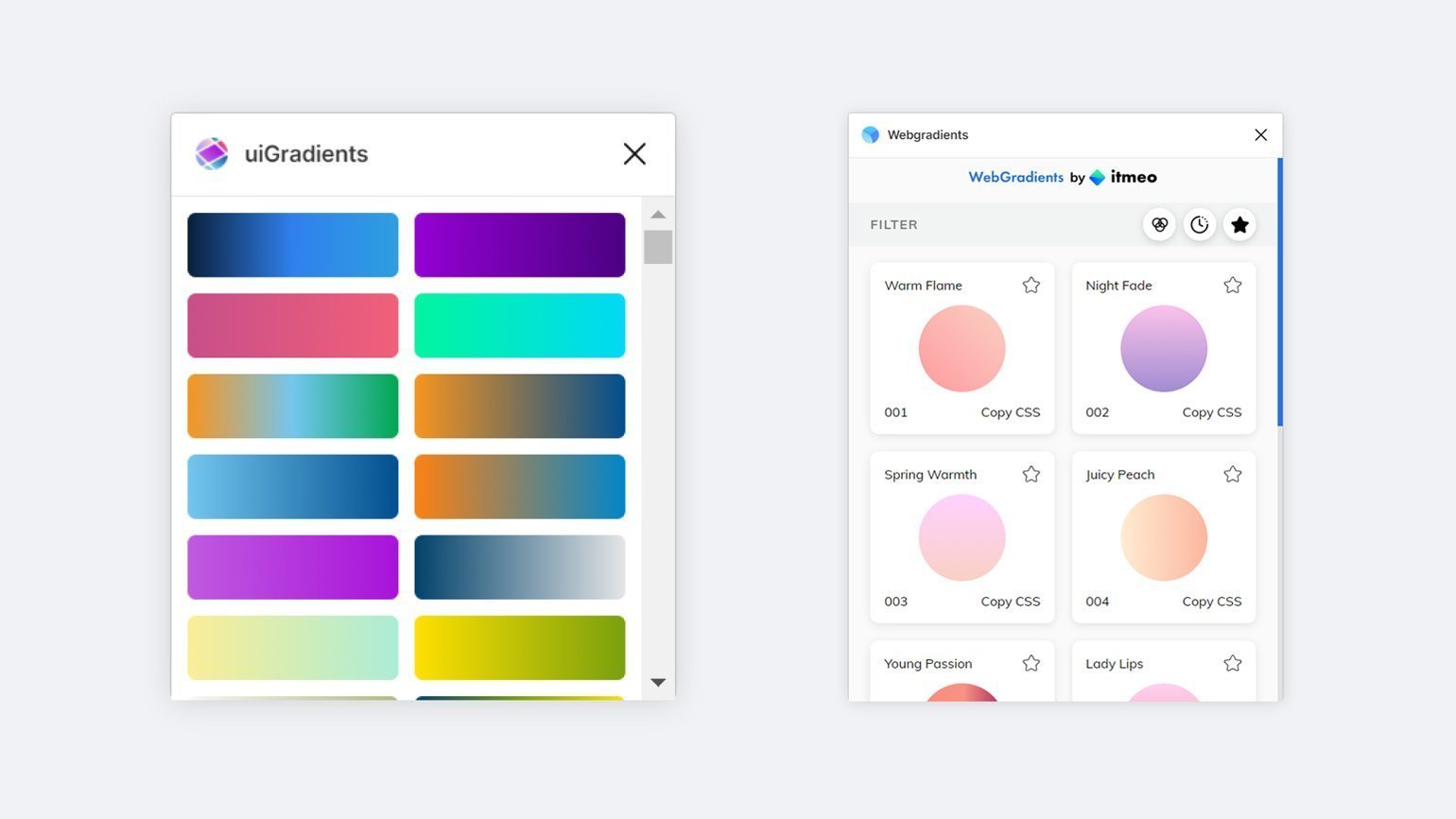
После запуска плагина достаточно выбрать подходящий градиент, который автоматически применится к фигуре.
В других редакторах градиенты часто добавляют в стандартные шаблоны, но можно воспользоваться веб-сервисом WebGradients, при помощи которого можно получить HEX-значения цветов градиента, CSS-код с параметрами или готовый к использованию файл PNG в размере 2400×2000 px.
Смягчение градиентов
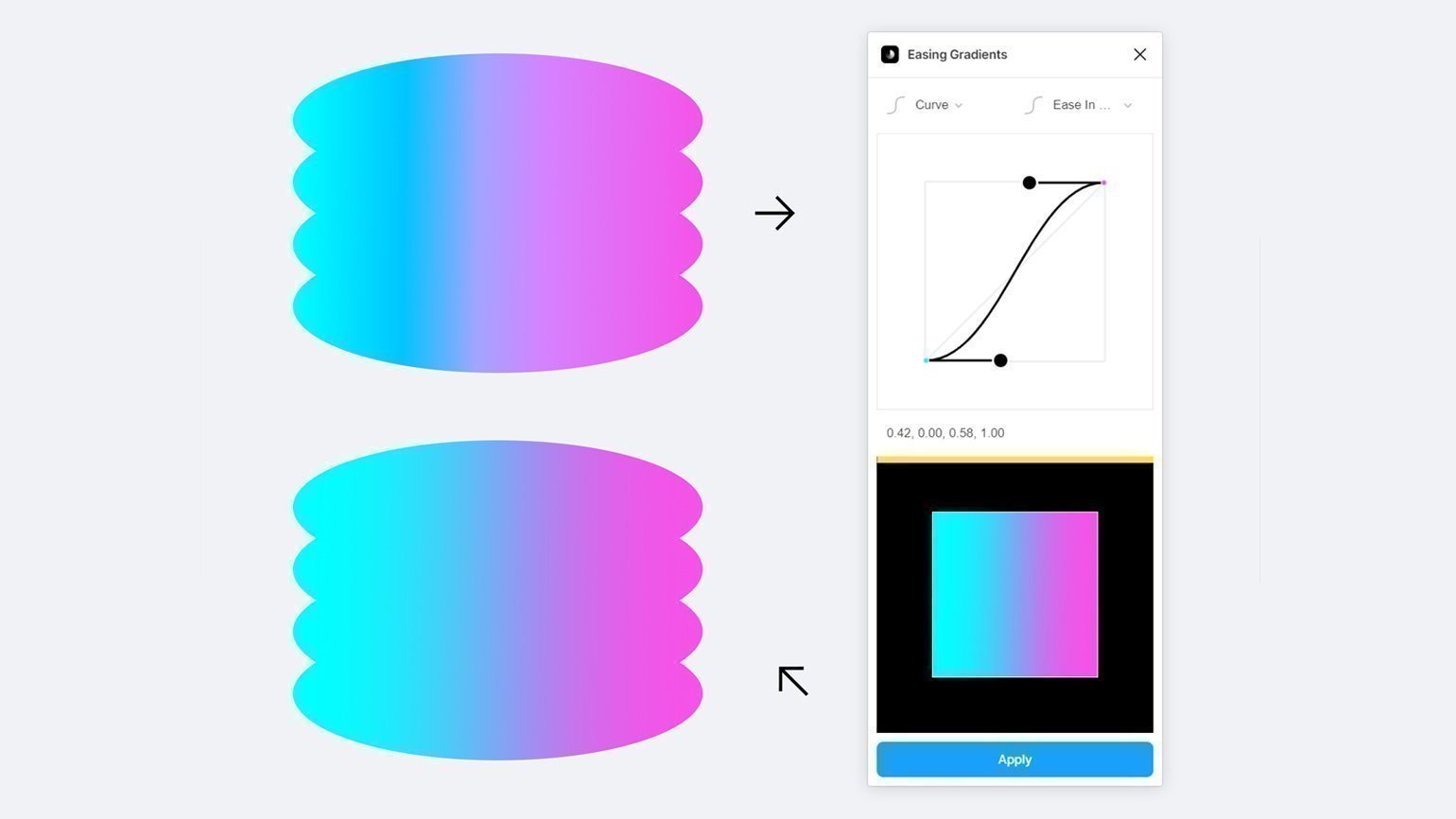
При построении градиентов иногда возникает проблема слишком резких и заметных переходов, а ведь вся суть градиента в плавности. Такие градиенты надо смягчать, по-английски это называется Easing Gradients.
Особенно хорошо это заметно на градиентах от чёрного к прозрачному, которые добавляют поверх изображения для улучшения читаемости надписи.
Решить проблему жёстких переходов можно, добавив промежуточные точки в градиент, а также сместив точки градиента в более подходящее место.
Однако этот метод очень неудобный и долгий. К счастью, в Figma есть плагин Easing Gradients, который позволяет смягчать градиенты автоматически. После его установки нужно выделить фигуру и запустить плагин. В появившемся окне выберите Curve и Easy In Out, после чего нажмите Apply. Если вариант Easy In Out не устраивает, то в окне плагина можно менять настройки.
Если же необходимо смягчить градиент быстро, то существует второй плагин с похожим названием Easing Gradient, только без s на конце. После установки выделите фигуру и запустите плагин. Поскольку он не открывает окно, то получается быстрее, однако этот быстрый метод работает на градиентах только с двумя цветами.
Также для смягчения градиентов с дальнейшим экспортом в CSS используют веб-ресурс Easing Gradients, где в простом редакторе можно смягчить двухцветный градиент.
Грязные градиенты → чистые градиенты
При построении градиента между некоторыми насыщенными цветами возникает область сероватого оттенка посередине. Связано это с внутренним устройством RGB-пространства. Выглядит такой градиент грязно.
Убрать ненасыщенную область сероватого оттенка можно несколькими методами.
Промежуточная точка
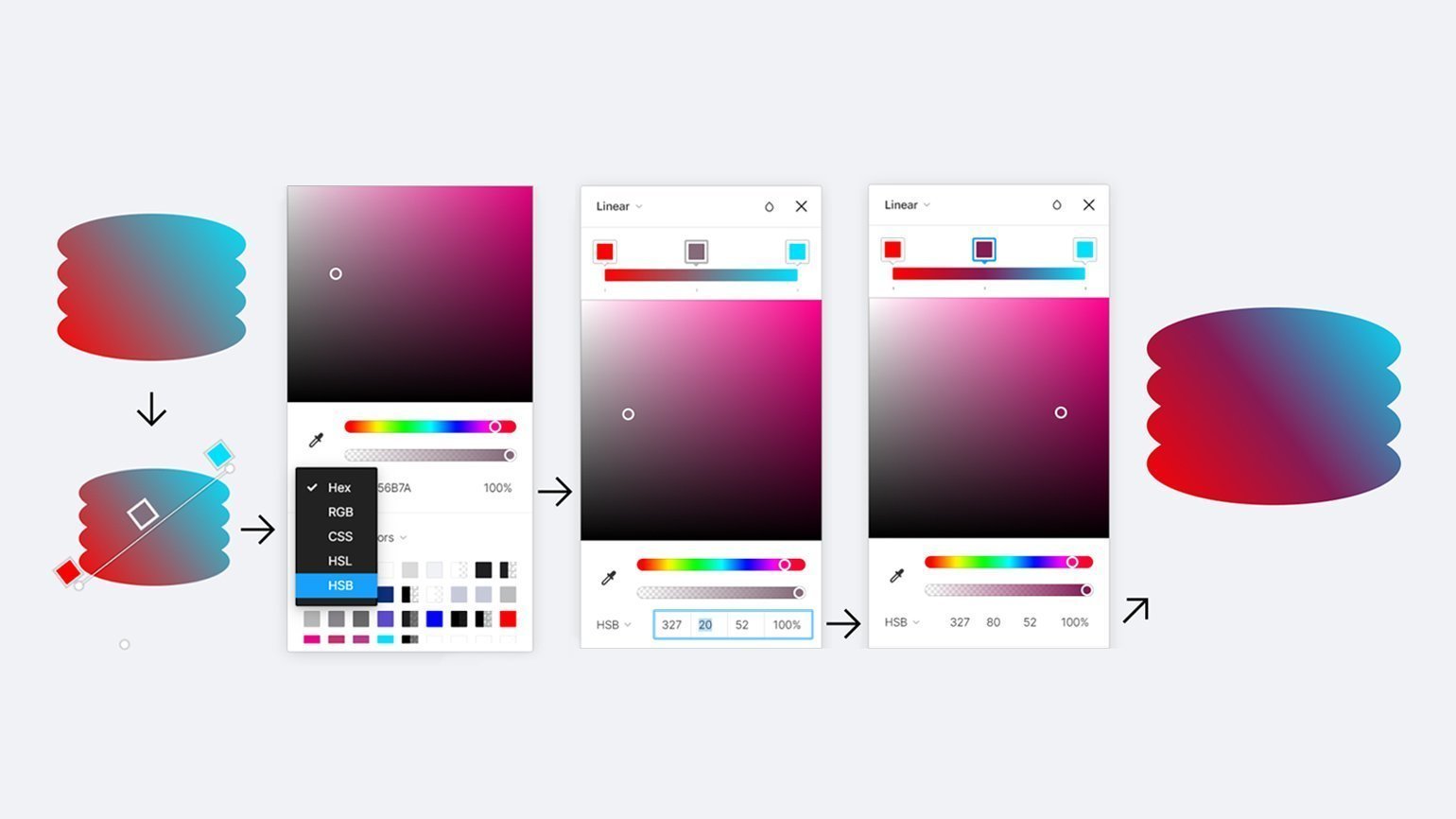
Во-первых, проблему можно решить вручную, добавив в градиент промежуточный цвет. Для этого нужно поставить точку посреди градиента, а затем повысить её насыщенность.
Увеличивать насыщенность можно на глаз, передвигая кружок на цветовом поле. А можно перейти в режим HSB и увеличить значение параметра S (Saturation — насыщенность) — это позволит сохранить цветовой тон и яркость без изменений.
По сути, в этом случае градиент будет строиться не по прямой от одного цвета к другому, а с использованием промежуточных точек ближе к краям цветового круга.
По дуге
Когда мы строим градиенты по прямой, линия проходит через ненасыщенную середину, поэтому градиенты лучше строить по дуге.
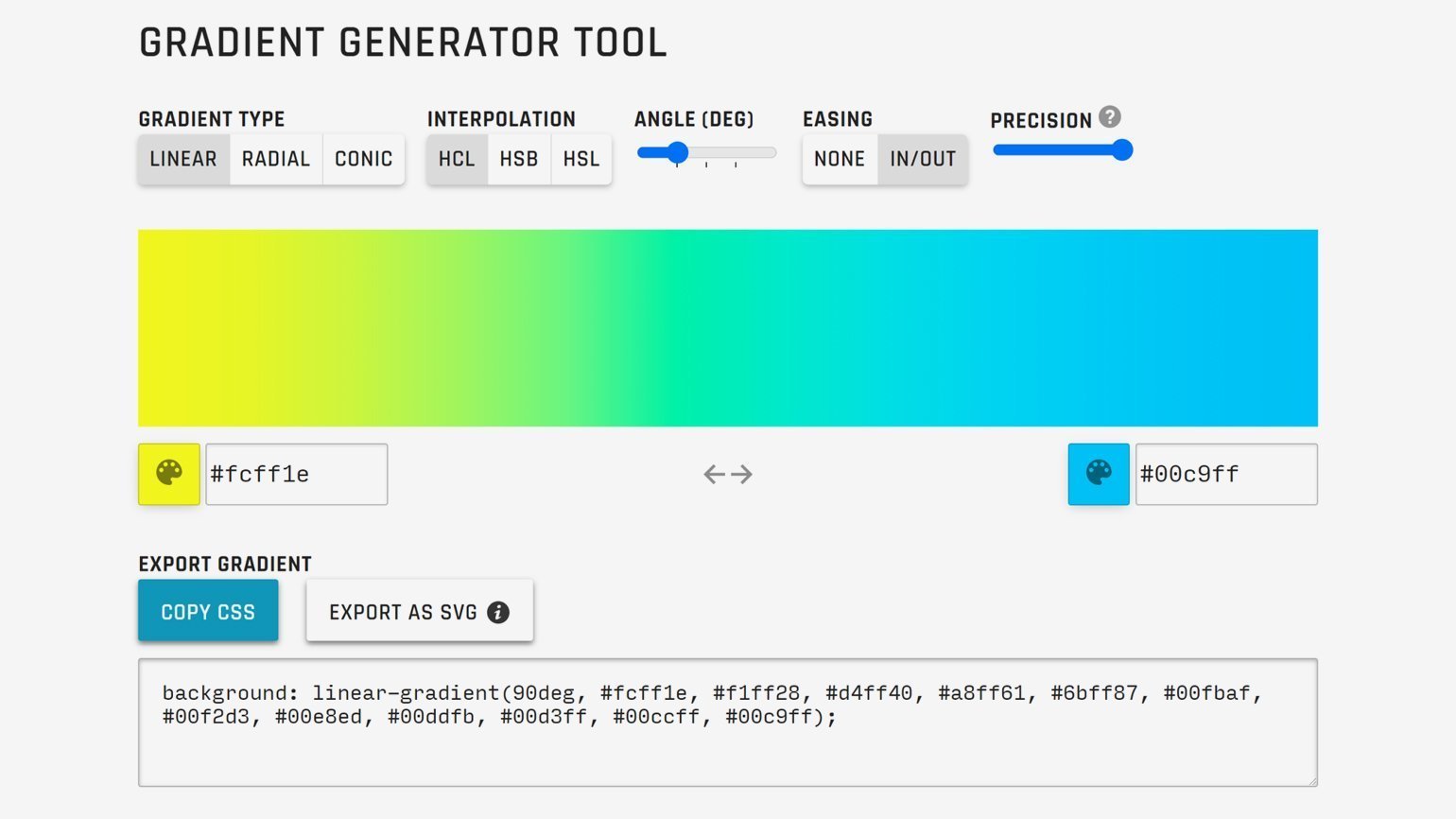
UI Gradient Generator строит градиенты по дуге автоматически. Сервис сам сделает плавный цветовой переход, обойдя ненасыщенную середину круга RGB.
Для более качественного градиента переключите параметр Easing (смягчение градиента) на In/ Out, а Precision (количество промежуточных точек градиента) выберите максимально возможный. Далее градиент можно перенести в Figma вручную, копируя каждый цвет, либо скачать SVG-файл с градиентом через кнопку Export as SVG. Этот векторный файл нужно перетащить мышью в графический редактор. Если свойство градиента требуется перенести на другой объект, то выделите в Figma объект с градиентом, в свойстве Fill выделите градиент и нажмите Ctrl (⌘) + С. Затем выделите другой объект и нажмите Ctrl (⌘) + V.
Для разработчиков, которым нужно вставить градиент на сайт при помощи CSS, сервис создаёт код, который можно скопировать.
RGB → LAB
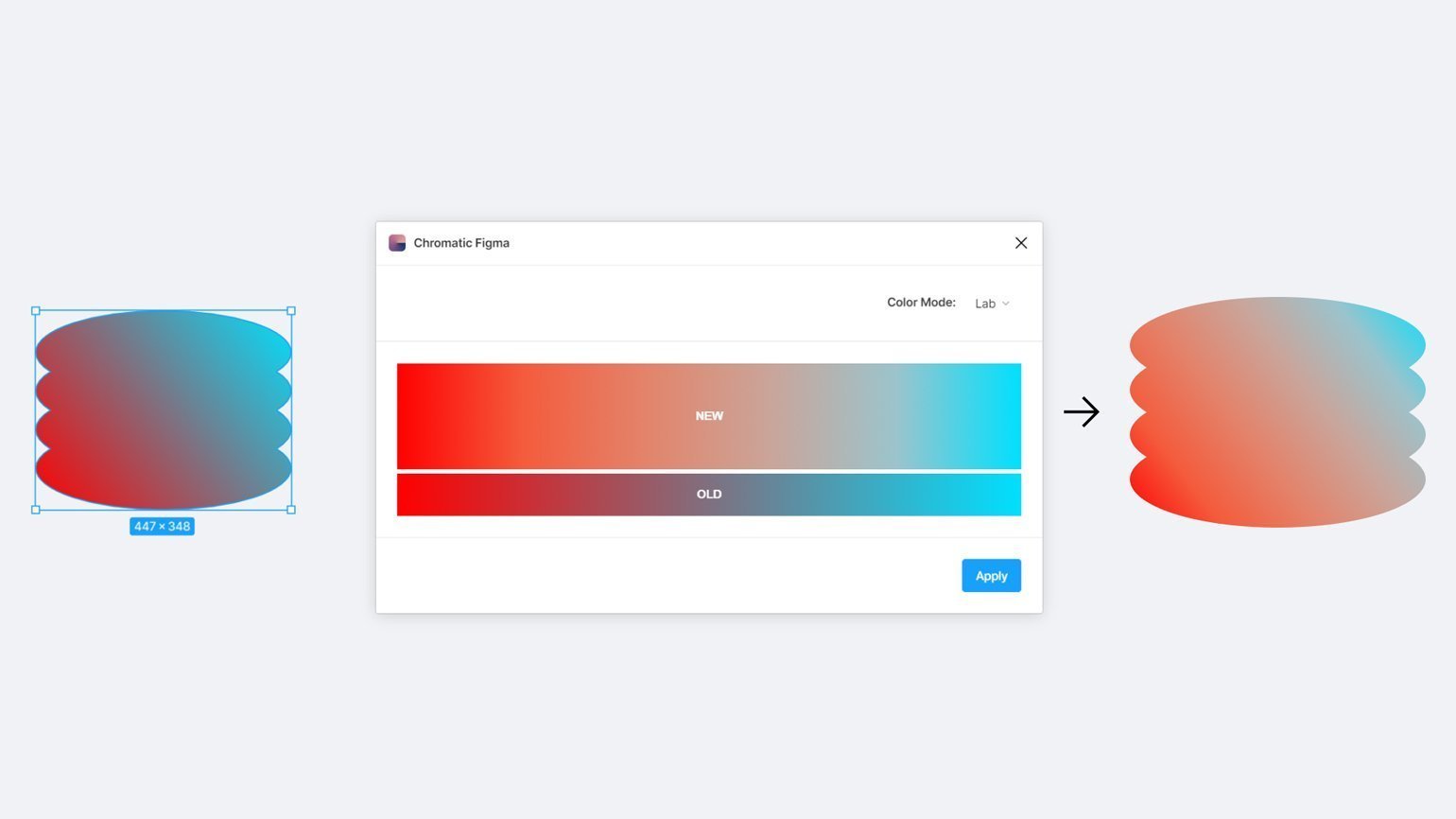
Раз проблема грязных градиентов связана с устройством RGB, то можно воспользоваться альтернативным цветовым пространством LAB. Оно спроектировано с учётом восприятия цветов глазом человека, поэтому градиенты будут не только плавными, но и с понятной логикой перехода цветов.
В Figma градиенты исправляются через плагин Chromatic Figma. Выделите фигуру с градиентом, запустите плагин Chromatic Figma, выберите Fix Gradient и нажмите Apply.
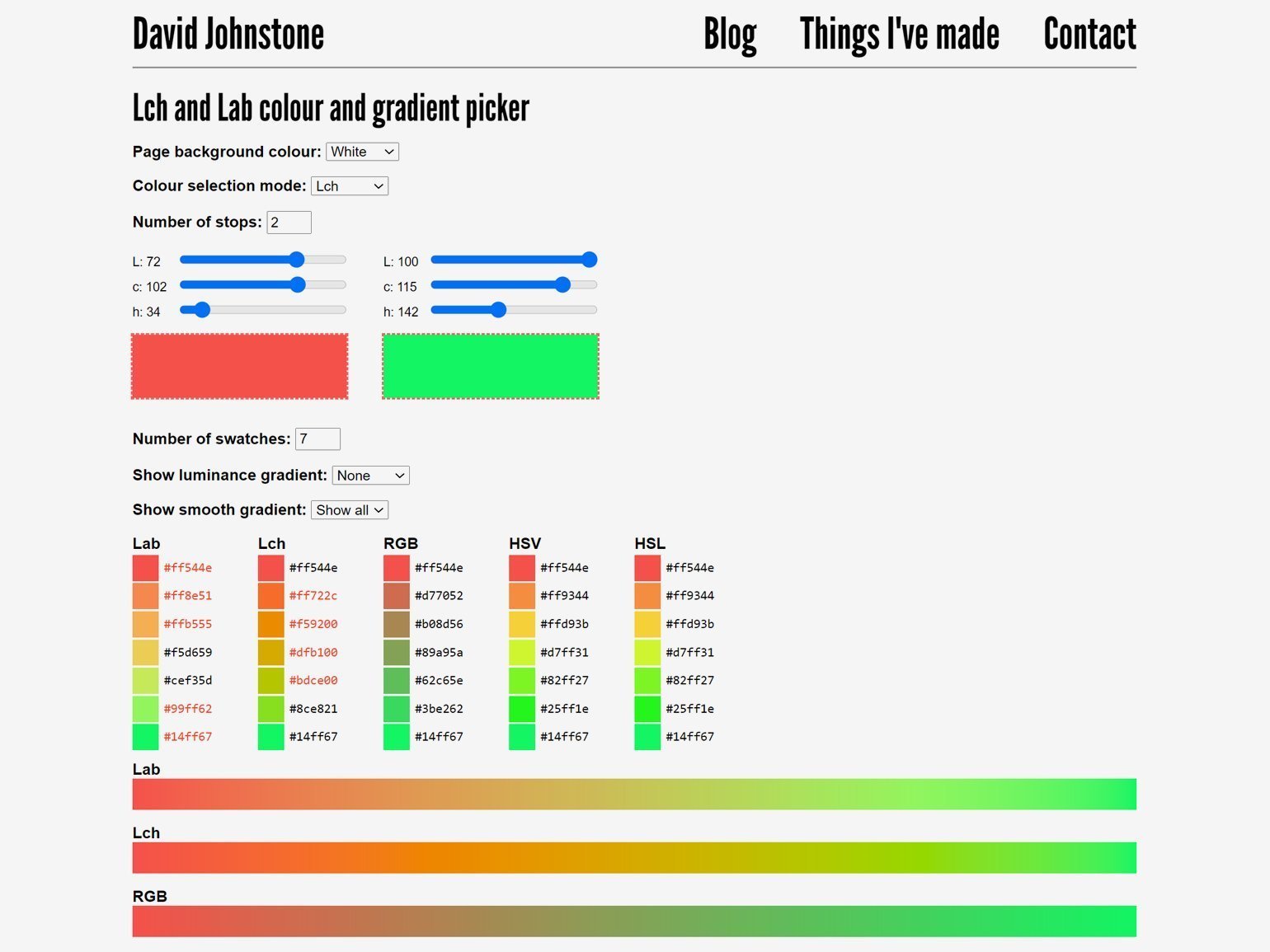
В качестве альтернативного метода создания градиента в LAB можно воспользоваться инструментом Lch and Lab colour and gradient picker Дэвида Джонстона.
Выберите два цвета, между которыми надо проложить градиент, и введите желаемое количество ступеней. Чем больше ступеней, тем более плавным будет переход.
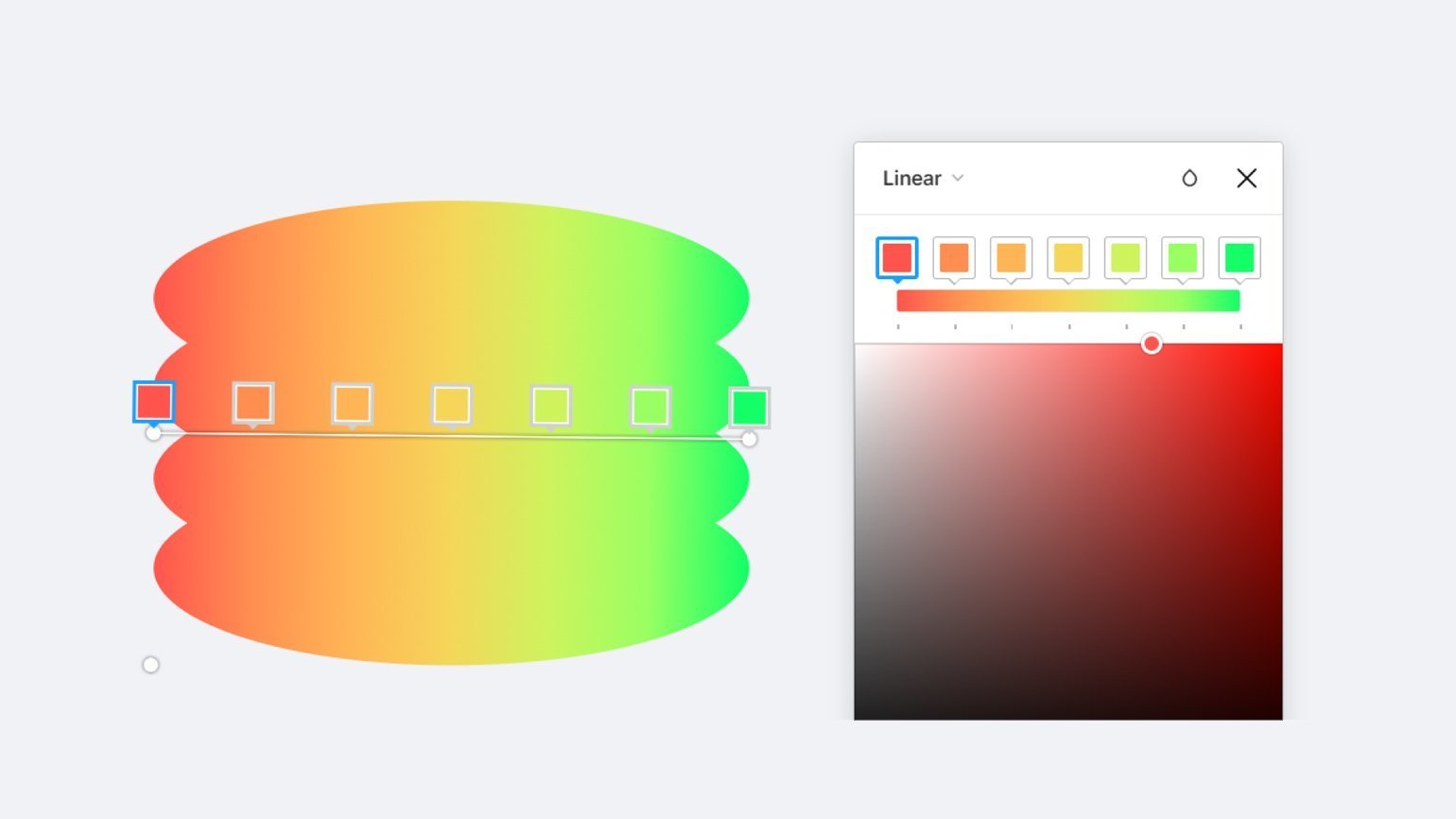
Затем перенесите цвета из колонки Lab в редактор.
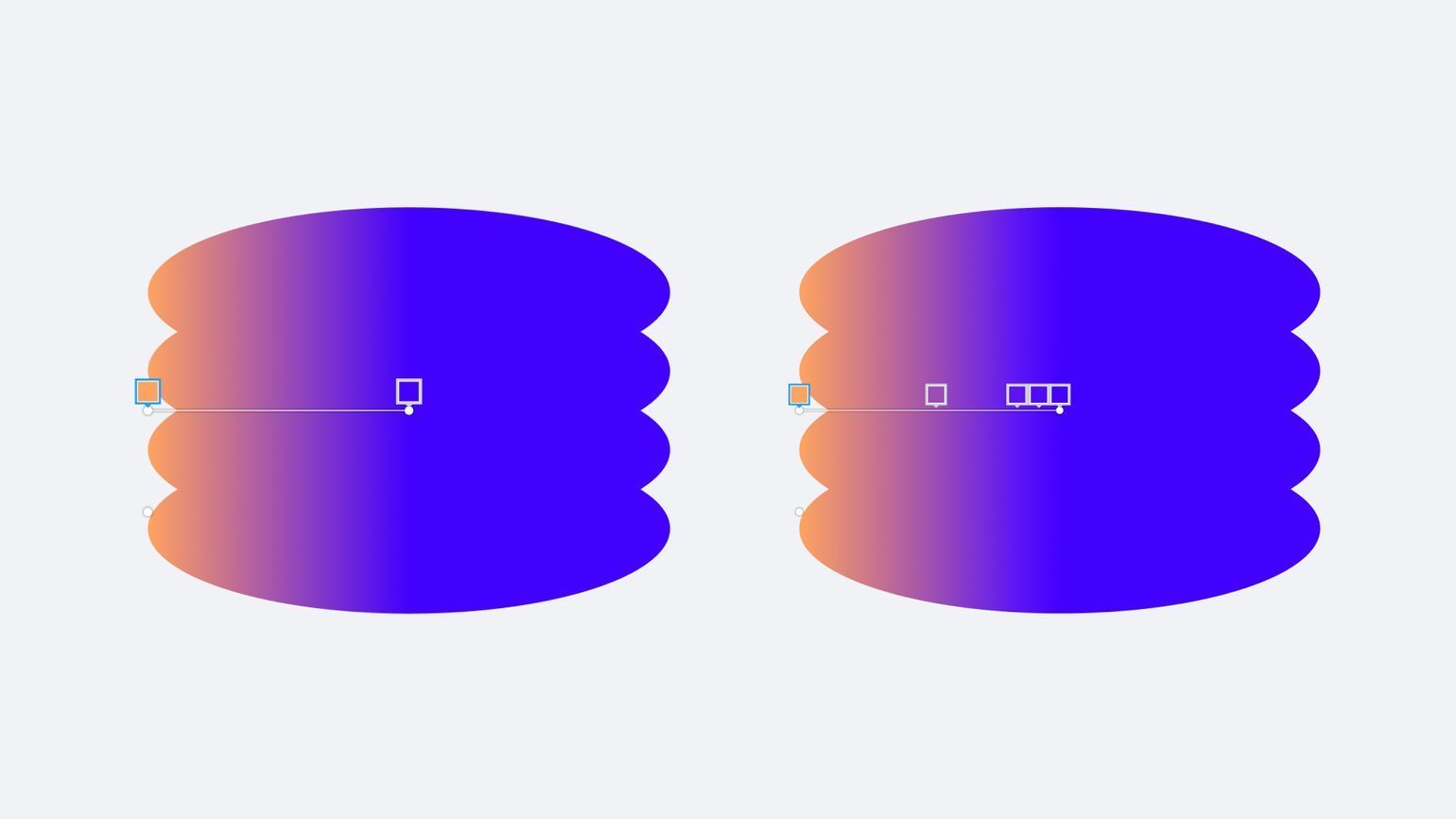
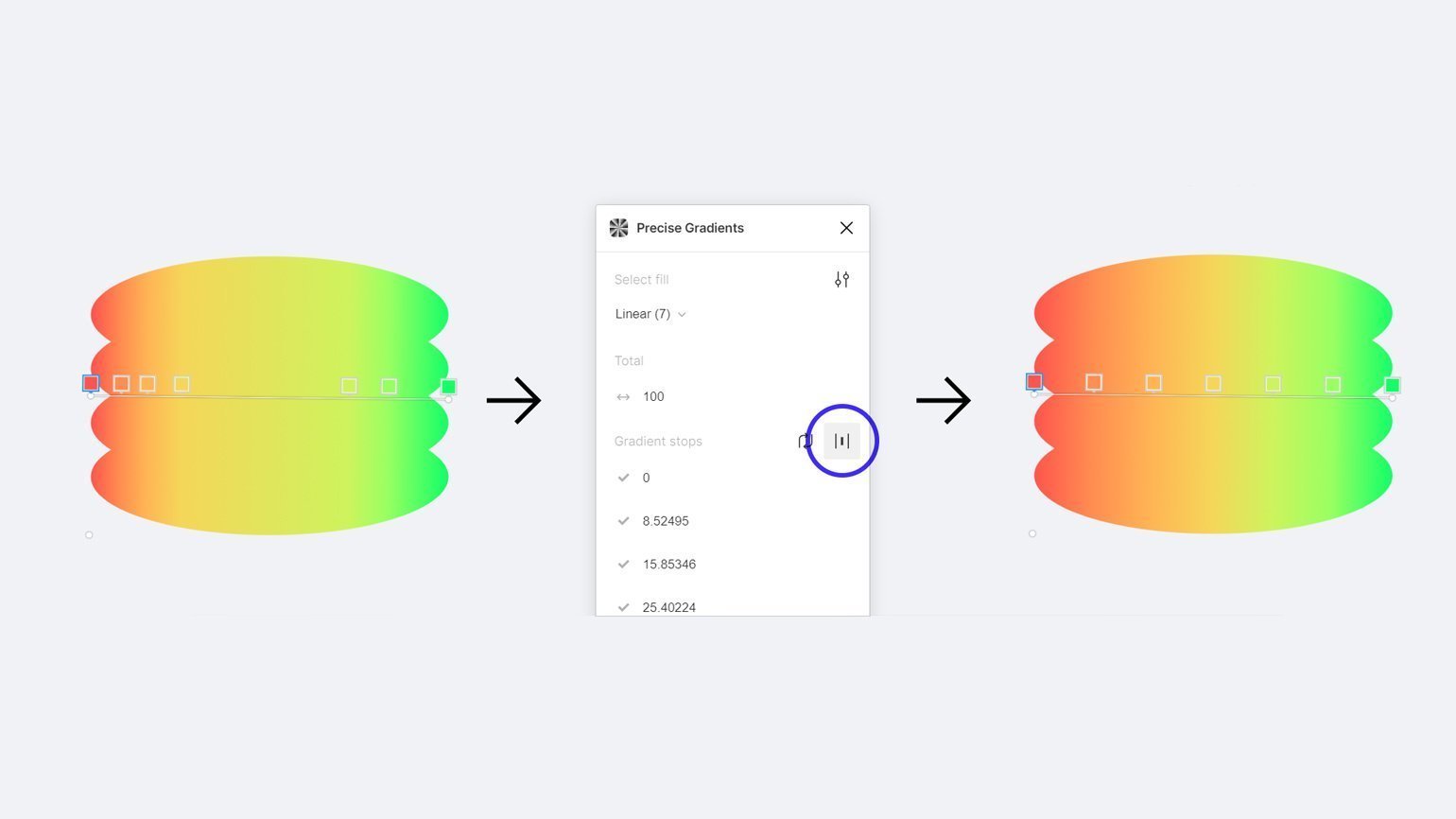
В Figma для того, чтобы расставить точки градиента на равном расстоянии, можно использовать плагин Precise Gradients. Сначала расставьте точки на случайном расстоянии, сохранив порядок цветов, затем запустите плагин и нажмите на иконку выравнивания, которая расположена в строке Gradient stops справа.
Сетчатые градиенты
Сетчатый градиент — сложный градиент на основе двухмерной сетки, также он называется mesh-градиентом. Создавать такой градиент нужно в специальных редакторах, поскольку добиться чего-то подобного с помощью комбинации простых градиентов, о которых мы говорили выше, невозможно: наложение множества градиентов приведёт к искажению цветов, и результат сложно будет назвать красивым.
В 2020–2021 годах мода на сетчатые градиенты набрала обороты — они действительно выглядят очень эффектно, и поэтому не удивительно, что дизайнеры их любят.
Естественно, как и с обычными градиентами, сетчатые можно выбрать из наборов готовых, например на meshgradients.design или products.ls.graphics. Но с точки зрения уникальности гораздо эффективнее делать mesh-градиенты самостоятельно.
Плагин Mesh Gradient в Figma
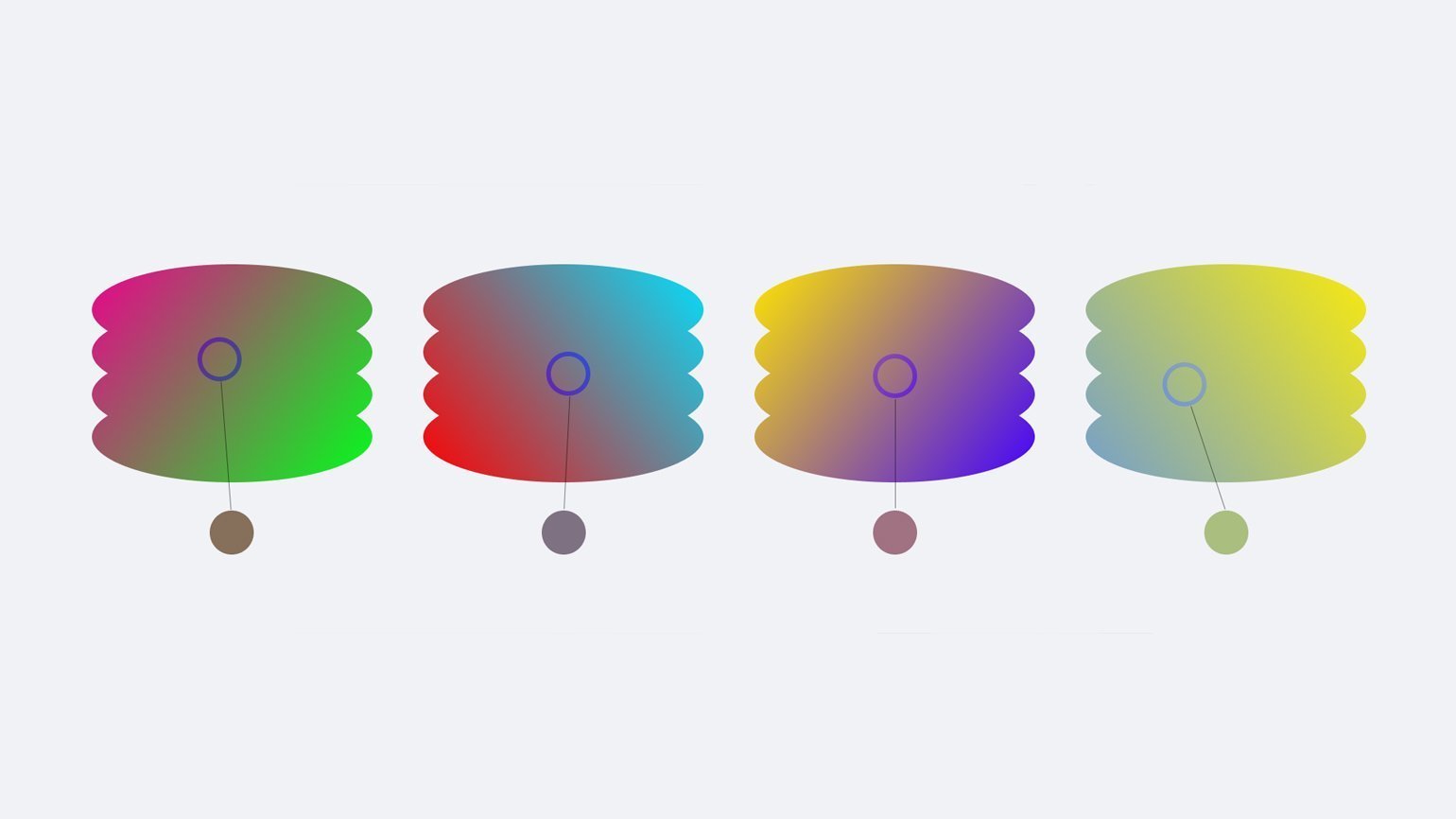
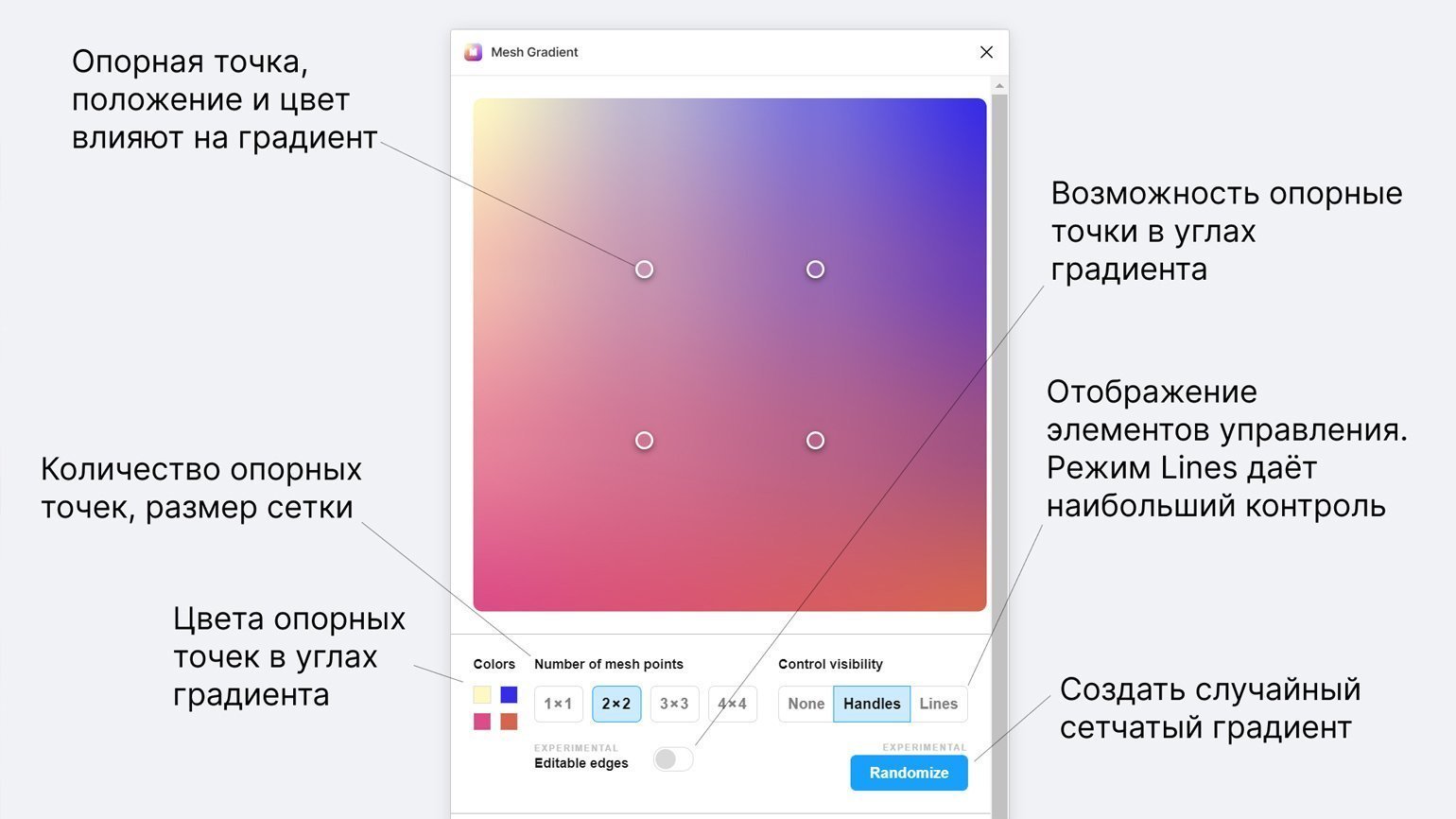
Для создания сетчатого градиента в Figma нужно использовать плагин Mesh Gradient. На плоскости устанавливаются опорные точки, которые будут «вершинами» градиента — краска по ним будет «стекать», смешиваясь с краской с других «вершин». На краях плоскости точки установлены по умолчанию.
Рассмотрим интерфейс плагина. В нём можно настроить размер сетки, цвета из углов градиента, отображение элементов управления, а также управление опорными точками mesh-градиента. Для ленивых сделана кнопка Randomize, которая создаёт случайный сетчатый градиент.
Чтобы включить отображение сетки, проходящей через опорные точки, в параметре Control visibility нужно переключиться на режим Lines. Параметры опорной точки: положение, цвет, регулировки сетки.
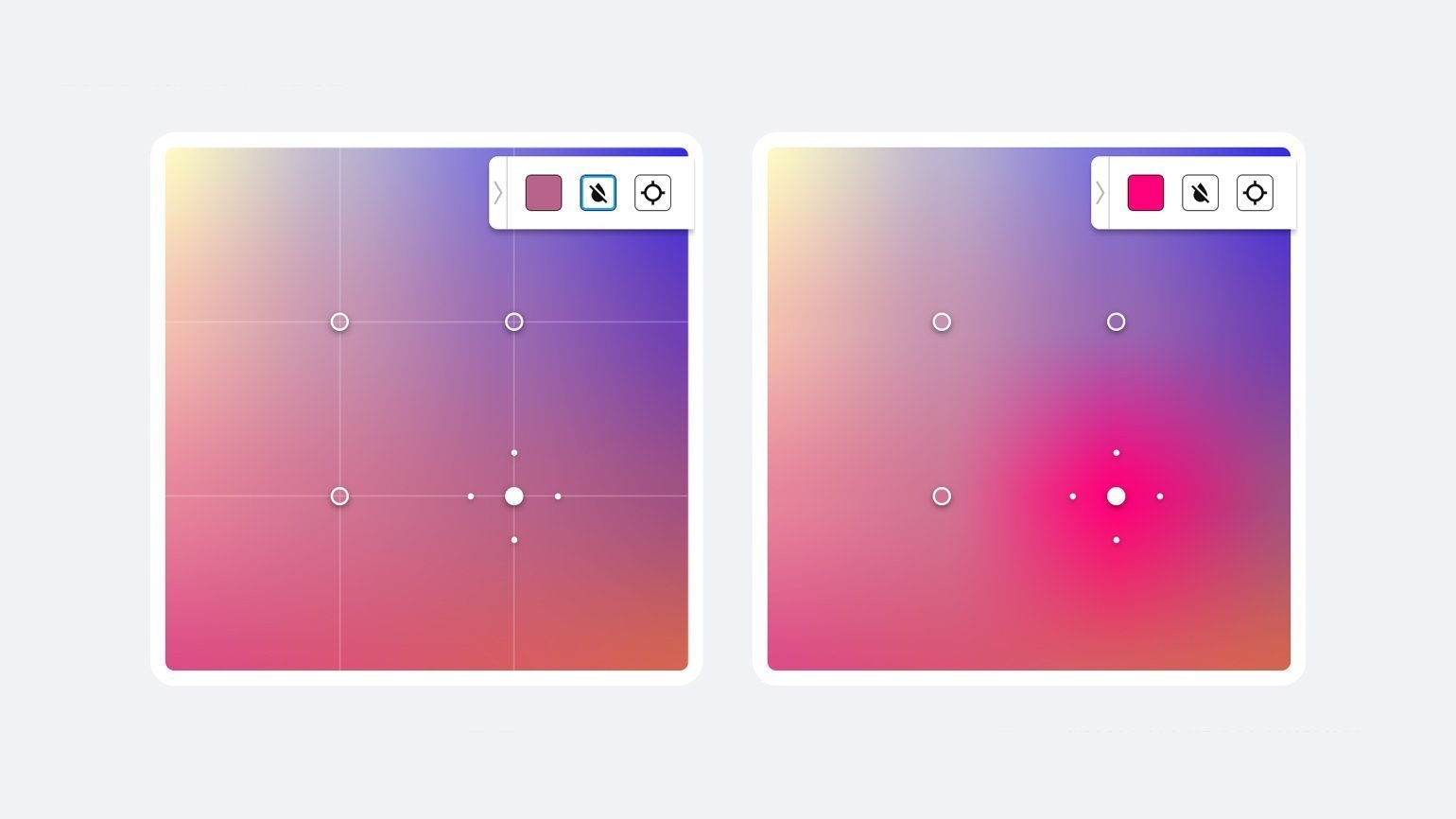
Цвет градиента по умолчанию задаётся исходя из начального положения опорной точки в сетке и значений цветов на углах — всё это можно менять, что повлечёт изменение градиента.
Положение точки: чем ближе точка к соседней или краю сетки, тем грубее переход, чем дальше — тем плавнее. Ну и, естественно, это положение влияет на место, откуда краска будет разливаться по сетке.
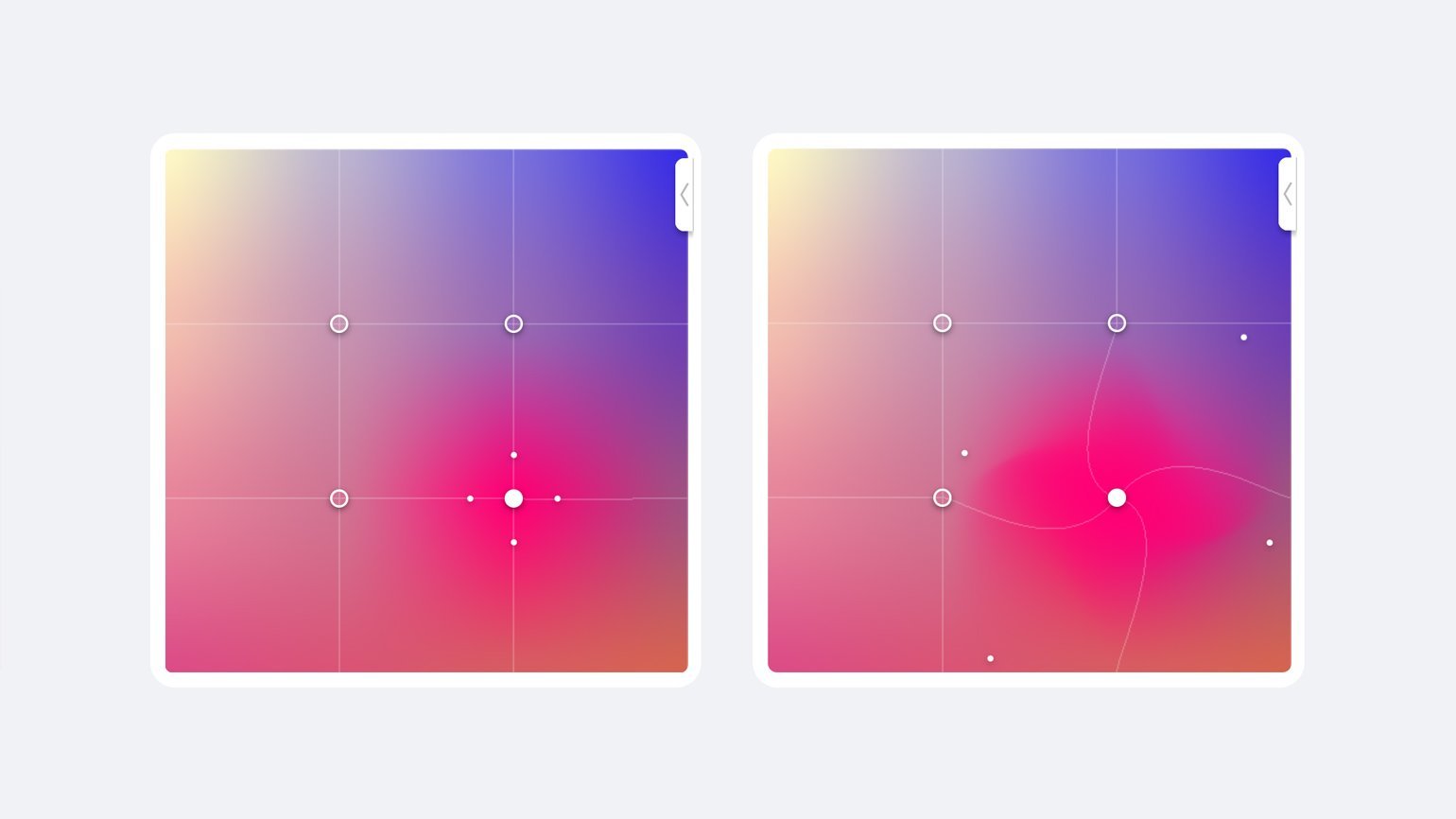
Регулировки сетки: по умолчанию точки расположены на углах внутреннего квадрата, однако их положение можно изменять. Это влияет на то, насколько сильно и в каком направлении будет распространяться цвет точки. В отображении Lines хорошо заметно, как регулировки влияют на форму сетки.
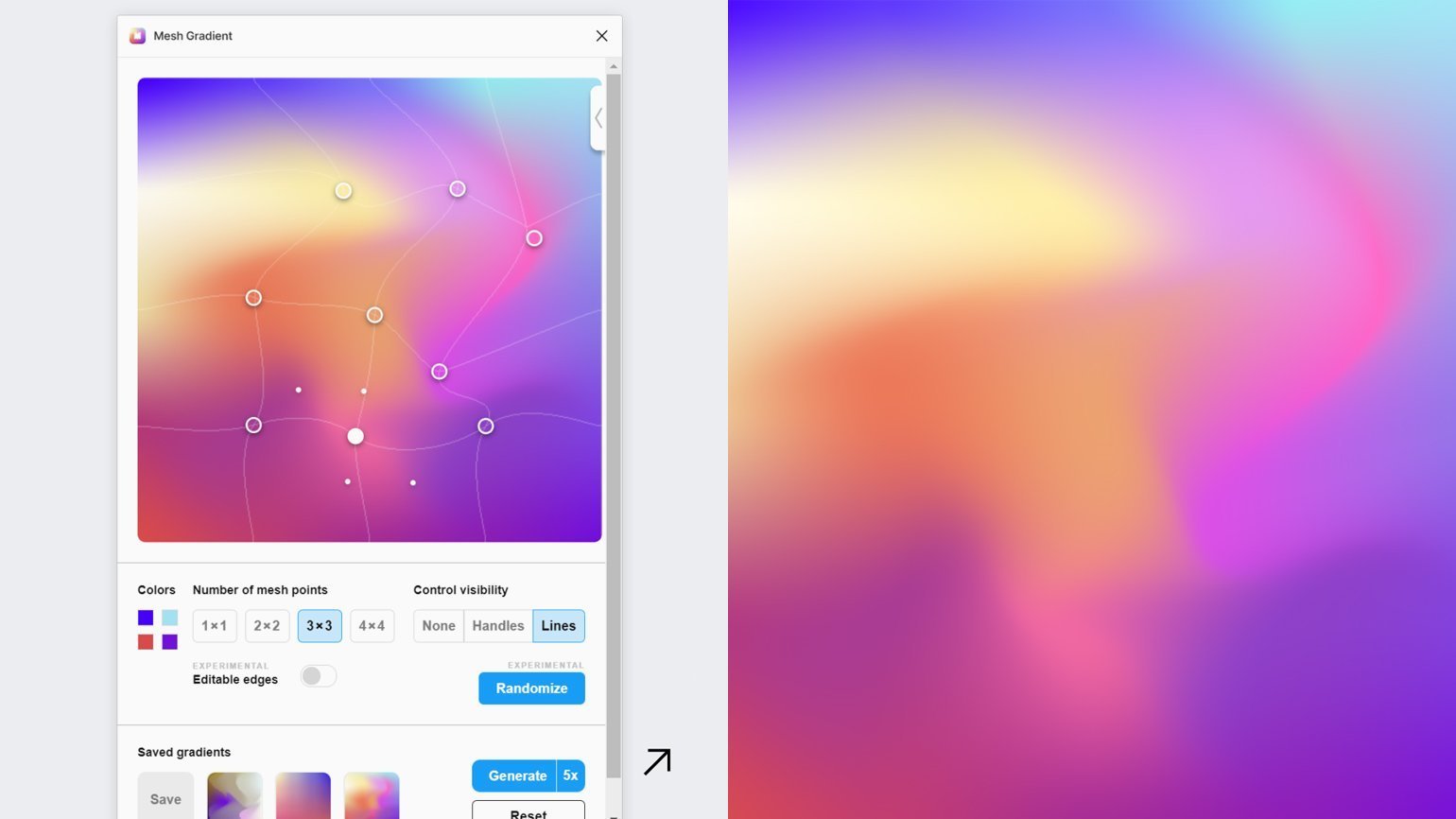
Теперь остаётся только нарисовать красивый градиент, используя положение точек и цвета углов. Можно добавить дополнительные точки. Затем выберите размер в правой части кнопки Generate: размер « 1x» создаёт файл в размере 512×512 px, размер « 5x» — 2560×2560 px. Теперь можно нажать на кнопку Generate.
В результате плагин создаст красивый сетчатый градиент в формате PNG. А если нажать на кнопку Save перед Generate, то он сохранится в коллекцию.
Веб-сервис Mesh
Принцип работы сервиса Mesh очень сильно отличается от плагина Figma. В нижней части экрана задаются цвета углов, а для создания градиента используются два окна.
В левом окне положение точки влияет на то, с какой силой она будет распространять цвет: чем ближе точка к углу, тем больше её цвета будет на градиенте в правой части. Положение точек в правом окне влияет на взаимодействие цветов друг с другом: чем точки ближе, тем переход более резкий, чем дальше — тем более плавный.
Чтобы добавить точку, нужно кликнуть мышью в произвольном месте, для удаления — нажать на точку, удерживая Shift. Минимальное количество точек — 4, максимальное — 11.
Описать работу сервиса сложнее, чем им пользоваться, поэтому просто переходите в Mesh и создавайте красоту. После создания нажмите Export в правом верхнем углу и сохраните градиент в размере 2000×2000 рх в формате PNG.
Подготовка градиентов к печати
Во-первых, лучше сразу перевести макет в цветовое пространство CMYK, потому что некоторых цветов из модели RGB в модели CMYK нет.
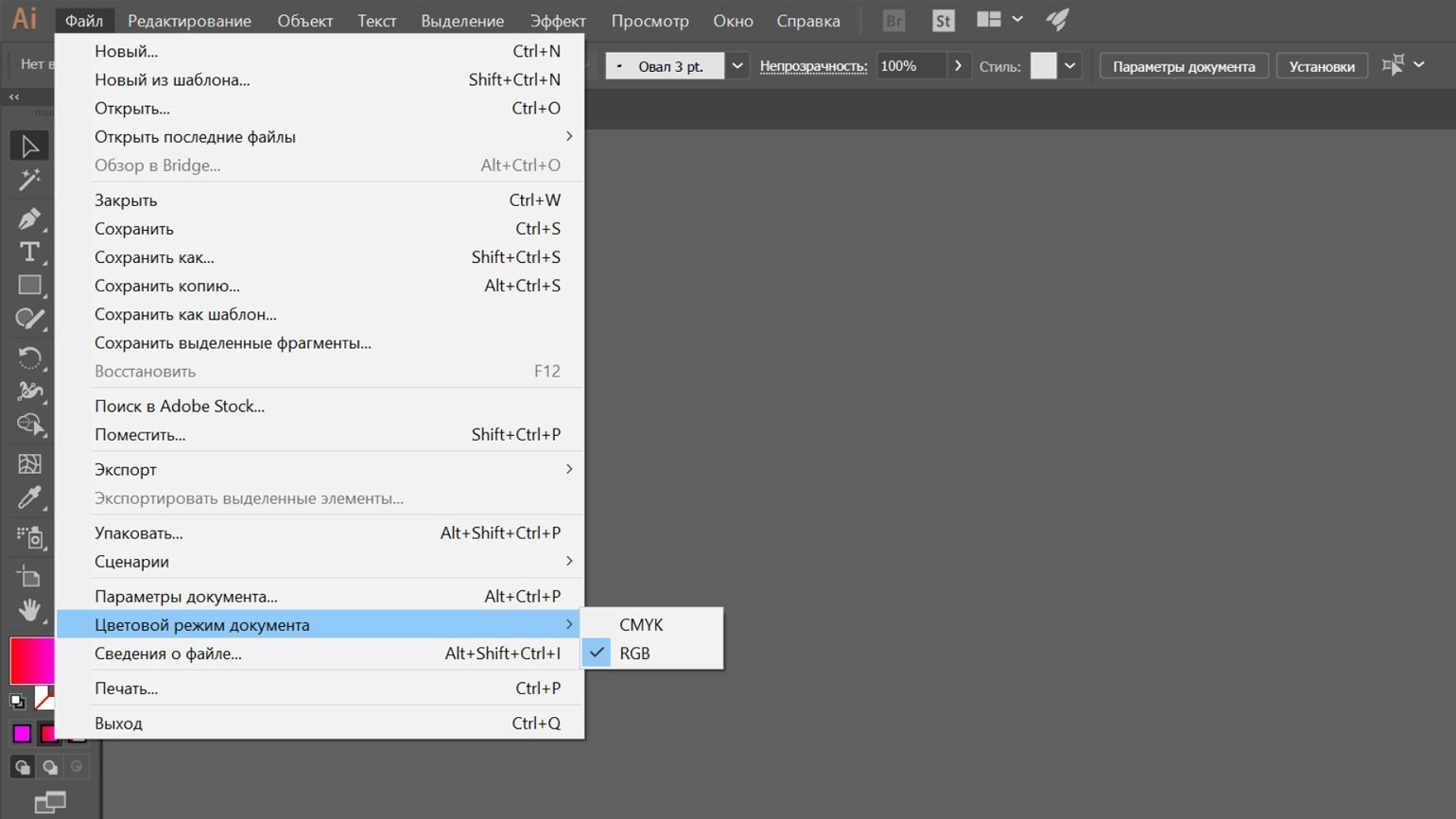
Переключение в режим CMYK в разных редакторах отличается, но мы остановим свой выбор на Adobe Illustrator как одной из самых популярных программ для графического дизайна и допечатной подготовки. Поэтому, открыв файл, выберите меню « Файл», перейдите в пункт « Цветовой режим документа» и кликните по CMYK.
Далее надо позаботится о том, чтобы градиент при печати не стал «ступенчатым». Иногда возникает неприятная ситуация, когда градиент на экране отображается нормально, но при печати вместо плавных переходы получаются резкими.
Некоторые специалисты по допечатной подготовке советуют растрировать градиент. По умолчанию градиент — элемент векторной графики, то есть код, который финальное устройство интерпретирует в графику. Некоторые принтеры плохо справляются с печатью таких градиентов. В случае растрирования градиент превратится в картинку ещё в графическом редакторе — каждый его пиксель будет иметь свой цвет.
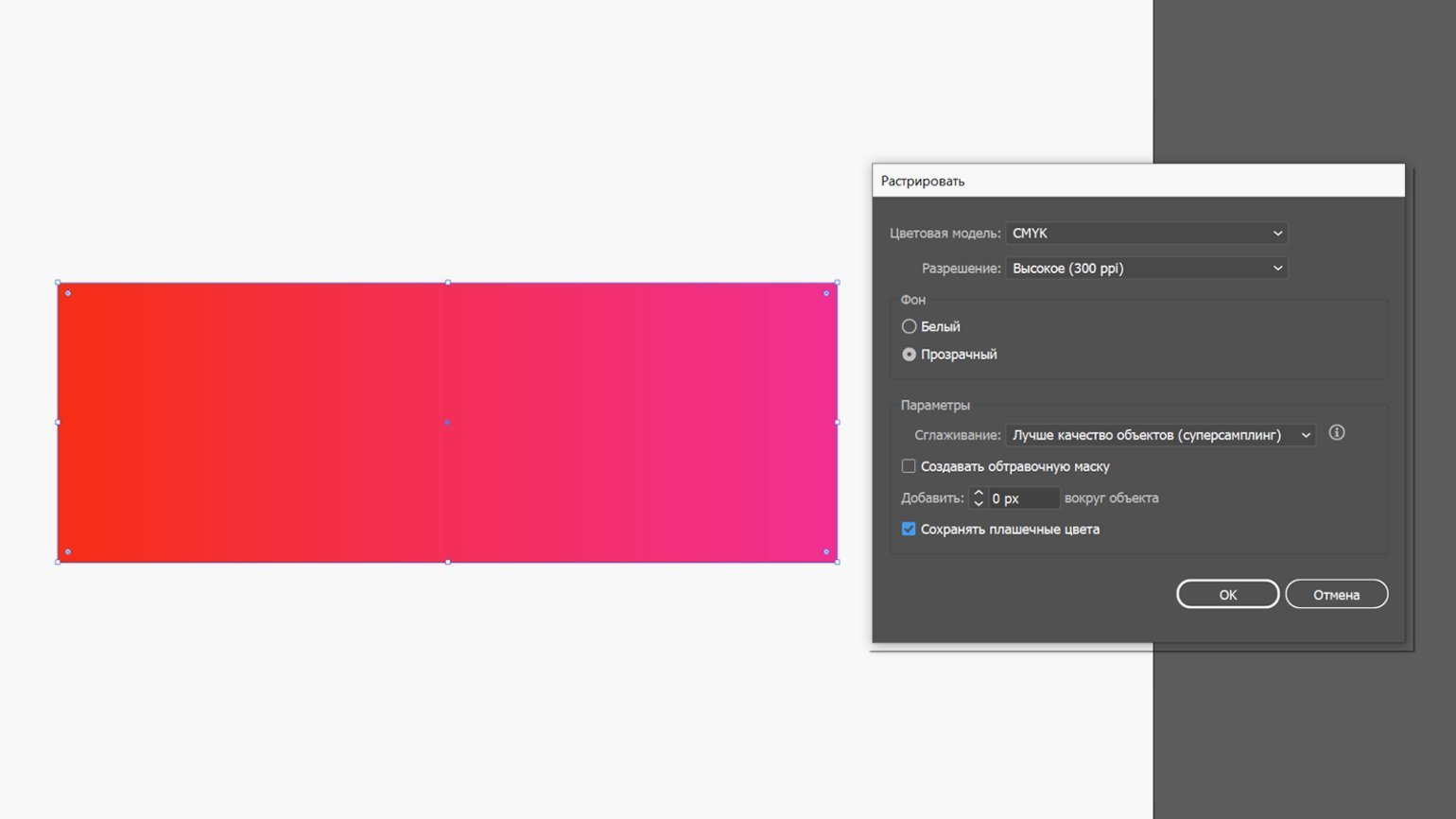
В Adobe Illustrator для растрирования нужно выделить объект с градиентом, затем перейти в меню « Объект» и выбрать « Растрировать…», после чего нажать на ОК.
В дополнение к растрированию также рекомендуют добавить шум — он смажет градиент и сделает его более равномерным.
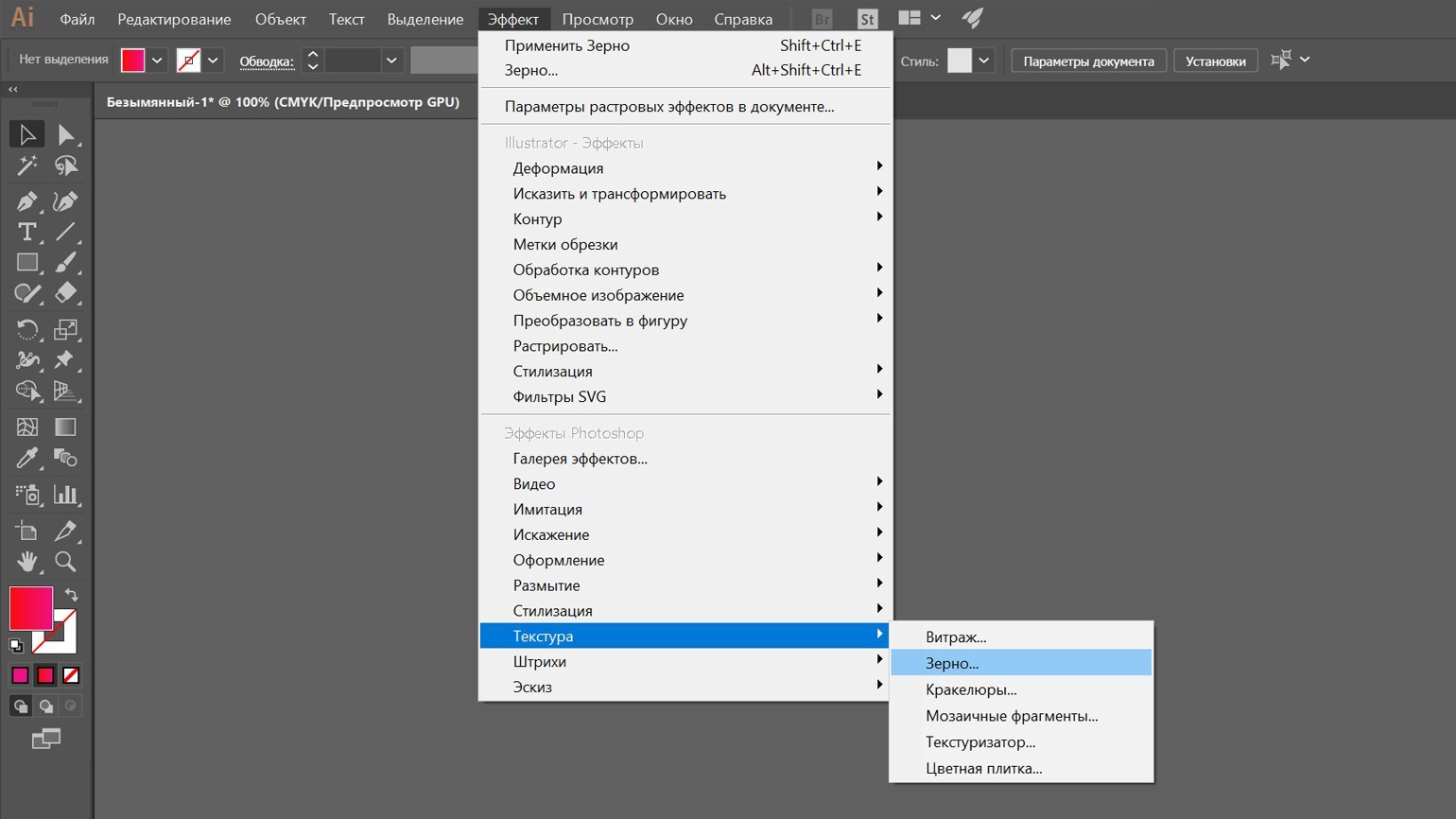
В Adobe Illustrator для добавления шума нужно выделить объект, затем перейти в меню « Эффект», выбрать в нем « Текстура» и затем « Зерно». В появившемся окне выставите степень зернистости и нажмите ОК.
Описанный способ растрирования градиента подходит для любых редакторов, не только для Adobe Illustrator. Но другие программы могут предложить и альтернативные методы. Их надо изучать на официальных ресурсах производителя программы, а также тематических форумах.
Стоит понимать, что после растрирования градиент нельзя будет редактировать, так что растрировать нужно непосредственно при допечатной подготовке, не раньше.
Как итог
Работа с градиентами требует не только отменного художественного вкуса и знаний колористики, но и серьёзной технической базы.
1. Не ограничивайтесь стандартными инструментами. При работе в Figma используйте плагины:
2. Если вы работаете с другим редактором или не хотите устанавливать плагин, то используйте онлайн-сервисы:
3. Не стоит и пытаться создать сетчатый градиент стандартными средствами. Используйте:
4. Прокачайте знания по теории цвета, в этом вам помогут наши материалы:
обложка: Оля Ежак для Skillbox Media