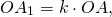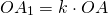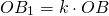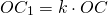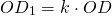что такое гомотетия в геометрии

Гомотетия

Гомотетия — это преобразование, при котором каждой точке A ставится в соответствие точка A1, лежащая на прямой OA, по правилу

где k — постоянное, отличное от нуля число, O — фиксированная точка.

Точка O называется центром гомотетии, число k — коэффициентом гомотетии.

гомотетия с коэффициентом k>0

Чтобы построить четырёхугольник, гомотетичный 4-угольнику ABCD с центром гомотетии в точке O и коэффициентом k, k>0, нужно провести лучи с началом в точке O, проходящие через вершины A, B, C, D, отложить на них отрезки соответствующей длины:

и соединить вершины A1, B1, C1и D1 отрезками.

При k

и соединить вершины A1, B1, C1 отрезками.

При гомотетии с коэффициентом k=1 каждая точка переводится сама в себя.

Гомотетия есть преобразование подобия. Следовательно, гомотетия обладает свойствами подобия.

Свойства преобразования гомотетии

1) При гомотетии прямые переходят в прямые, полупрямые- в полупрямые, отрезки — в отрезки, углы — в углы.

2) Сохраняются углы между полупрямыми (соответственно, сохраняется параллельность прямых).

Стороны гомотетичных фигур пропорциональны. а углы — равны.

Источник

Свойства, типы и примеры гомотетии

homotecia представляет собой геометрическое изменение в плоскости, где расстояния от фиксированной точки, называемой центром (O), умножаются на общий коэффициент. Таким образом, каждая точка P соответствует другой точке P ‘, являющейся произведением преобразования, и они выровнены с точкой O.

homotecia

Чтобы гомотетия была выполнена, они должны соответствовать точка-точка и прямая-прямая, чтобы пары гомологичных точек были выровнены с третьей фиксированной точкой, которая является центром гомотетии..

Аналогично, пары линий, которые соединяют их, должны быть параллельными. Соотношение между такими сегментами является константой, называемой коэффициентом гомотетии (k); таким образом, что гомотетия может быть определена как:

Чтобы сделать этот тип преобразования, вы начинаете с выбора произвольной точки, которая будет центром гомотетии..

С этой точки отрезки линий рисуются для каждой вершины фигуры, которая должна быть преобразована. Масштаб, в котором выполняется воспроизведение нового рисунка, определяется по причине гомотетии (k)..

свойства

Одним из основных свойств гомотетии является то, что по причине гомотетии (k) все гомотетические фигуры схожи. Среди других выдающихся свойств являются следующие:

— Линии, проходящие через центр, трансформируются (они двойные), но точки, составляющие его, не являются двойными.

— Прямые, которые не проходят через центр, превращаются в параллельные линии; таким образом, углы гомотетии остаются неизменными.

— Образ сегмента с помощью гомотетии центра O и отношения k представляет собой отрезок, параллельный этому, и имеет k-кратную длину. Например, как видно на следующем изображении, сегмент AB с помощью гомотетики приведет к другому сегменту A’B ‘, так что AB будет параллельным A’B’, а k будет:

С другой стороны, гомотетия варьируется в зависимости от значения ее отношения (k), и могут возникнуть следующие случаи:

— Если константа k = 1, все точки фиксированы, потому что они трансформируются. Таким образом, гомотетическая фигура совпадает с оригиналом и преобразование будет называться тождественной функцией.

— Если k ≠ 1, единственной фиксированной точкой будет центр гомотетии (O).

— Если k> 1, размер преобразованного рисунка будет больше размера исходного.

— Да 0 0; то есть гомотетические точки находятся на одной стороне относительно центра:

Коэффициент пропорциональности или отношения сходства между прямыми гомотетическими фигурами всегда будет положительным.

Источник

Что такое гомотетия в геометрии

Документальные учебные фильмы. Серия «Геометрия».

Выберем ортонормированный репер (О, Е₁, E₂) так, чтобы точка О совпала с центром гомотетии. Если М (х, у) —произвольная точка плоскости, а точка M′ (х’, у’) — ее образ, то из формулы (1) получаем аналитическое выражение гомотетии:
. (3)

Рассмотрим простейшие свойства гомотетии.

1) Гомотетия с коэффициентом переводит прямую, не проходящую через центр гомотетии, в параллельную ей прямую, а прямую, проходящую через центр гомотетии, — в себя.

2) Гомотетия сохраняет простое отношение трех точек.

Из этих свойств следует, что гомотетия переводит отрезок в отрезок, луч в луч и полуплоскость в полуплоскость.

3) Гомотетия переводит угол в равный ему угол.

□ Пусть ВАС — данный угол, а В′ А′ С’ — образы точек В, А и С. По формуле (2) получаем:

Отсюда следует, что

4) Гомотетия сохраняет ориентацию плоскости.

Таким образом, если М (х, у) — произвольная точка плоскости, а М'(х′, у’) — ее образ в преобразовании то

где =1, если — преобразование подобия первого рода, и = — 1, если — преобразование подобия второго рода. Используя формулы (7), докажем теорему.

Теорема 2. Любое преобразование подобия, отличное от движения, имеет одну и только одну неподвижную точку.

□ Пусть равенства (7) — аналитическое выражение данного преобразования подобия. Точка М (х, у) является неподвижной точкой этого преобразования тогда и только тогда, когда

Итак, существует шесть типов преобразования подобия, которые приведены в следующей таблице:

Это отображение называется гомотетией с центром Мо и коэффициентом m. Для двух точек M₁ и М₂ и их образов и из формулы (1) получаем:

Отсюда и следует сформулированное выше утверждение.

Теорема 1, сформулированная и доказанная (см. выше), полностью переносится на пространство, т. е. любое преобразование подобия пространства с коэффициентом является произведением гомотетии с тем же коэффициентом и произвольным центром на некоторое движение. Отсюда следует, что подобие пространства переводит плоскость (прямую) в плоскость (прямую), параллельные плоскости (прямые) —в параллельные плоскости (прямые). Подобие сохраняет простое отношение трех точек, поэтому оно переводит отрезок в отрезок, луч — в луч, полуплоскость — в полуплоскость, полупространство — в полупространство. Подобие переводит угол в равный ему угол, взаимно перпендикулярные прямые (плоскости) — во взаимно перпендикулярные прямые (плоскости).
Точно так же, как и на плоскости, можно доказать, что любое преобразование подобия либо сохраняет ориентацию пространства, либо меняет ее. В первом случае оно называется преобразованием подобия первого рода, а во втором случае — преобразованием подобия второго рода. Таким образом, гомотетия с положительным коэффициентом является преобразованием подобия первого рода, а гомотетия с отрицательным коэффициентом (в частности, центральная симметрия, ) — преобразованием подобия второго рода.

Источник