что такое глубина рекурсии
PostgreSQL Antipatterns: «Бесконечность — не предел!», или Немного о рекурсии
Рекурсия — очень мощный и удобный механизм, если над связанными данными делаются одни и те же действия «вглубь». Но неконтролируемая рекурсия — зло, которое может приводить или к бесконечному выполнению процесса, или (что случается чаще) к «выжиранию» всей доступной памяти.
СУБД в этом отношении работают по тем же принципам — «сказали копать, я и копаю«. Ваш запрос может не только затормозить соседние процессы, постоянно занимая ресурсы процессора, но и «уронить» всю базу целиком, «съев» всю доступную память. Поэтому защита от бесконечной рекурсии — обязанность самого разработчика.
В PostgreSQL возможность использовать рекурсивные запросы через WITH RECURSIVE появилась еще в незапамятные времена версии 8.4, но до сих пор можно регулярно встретить потенциально-уязвимые «беззащитные» запросы. Как избавить себя от проблем подобного рода?
Не писать рекурсивные запросы
А писать нерекурсивные. С уважением, Ваш К.О.
На самом деле, PostgreSQL предоставляет достаточно большое количество функционала, которым можно воспользоваться, чтобы не применять рекурсию.
Использовать принципиально другой подход к задаче
Иногда можно просто взглянуть на задачу «с другой стороны». Пример такой ситуации я приводил в статье «SQL HowTo: 1000 и один способ агрегации» — перемножение набора чисел без применения пользовательских агрегатных функций:
Такой запрос можно заменить на вариант от знатоков математики:
Использовать generate_series вместо циклов
Допустим, перед нами стоит задача сгенерировать все возможные префиксы для строки ‘abcdefgh’ :
Изменить структуру БД
Например, у вас есть таблица сообщений форума со связями кто-кому ответил или тред в социальной сети:
Ну и типовой запрос загрузки всех сообщений по одной теме выглядит примерно так:
Но раз у нас всегда нужна вся тема от корневого сообщения, то почему бы нам не добавлять его идентификатор в каждую запись автоматом?
Теперь весь наш рекурсивный запрос может быть сведен всего лишь к вот такому:
Использовать прикладные «ограничители»
Если поменять структуру базы мы не в силах по каким-то причинам, давайте посмотрим, на что можно опереться, чтобы даже наличие ошибки в данных не приводило к бесконечному выполнению рекурсии.
Счетчик «глубины» рекурсии
Просто увеличиваем счетчик на единицу на каждом шаге рекурсии вплоть до момента достижения предела, который мы считаем заведомо неадекватным:
Pro: При попытке зацикливания мы все равно сделаем не более указанного лимита итераций «вглубь».
Contra: Нет гарантии, что мы не обработаем повторно одну и ту же запись — например, на глубине 15 и 25, ну и дальше будет каждые +10. Да и про «вширь» никто ничего не обещал.
Формально, такая рекурсия не будет бесконечной, но если на каждом шаге количество записей увеличивается по экспоненте, мы все хорошо знаем, чем это кончается…
Хранитель «пути»
Поочередно дописываем все встретившиеся нам по пути рекурсии идентификаторы объектов в массив, который является уникальным «путем» до него:
Pro: При наличии цикла в данных мы абсолютно точно не станем обрабатывать повторно одну и ту же запись в рамках одного пути.
Contra: Но при этом мы можем обойти, буквально, все записи, так и не повторившись.
Ограничение длины пути
Чтобы избежать ситуации «блуждания» рекурсии на непонятной глубине, мы можем скомбинировать два предыдущих метода. Или, если не хотим поддерживать лишних полей, дополнить условие продолжения рекурсии оценкой длины пути:
Основы программирования — второй семестр 08-09; Михалкович С.С.; III часть
Содержание
Рекурсия
Основные определения
Рекурсией называется определение объекта через такой же объект.
В данном примере рекурсивной частью определения является » ',' «.
Замечание 1. Рекурсивное определение, будучи конечным, определяет бесконечное множество объектов.
Заметим также, что можно определить и по-другому:
Определение (1) называют леворекурсивным, а (2) — праворекурсивным.
Замечание 2. В рекурсивном определении обязательно (. ) должна присутствовать нерекурсивная часть.
Рекурсивное определение может быть косвенным:
по одной из ветвей рекурсивного определения упоминается объект, в определении которого, в свою очередь, по одной из ветвей определяется исходный объект.
В данном примере имеется как прямое, так и косвенное рекурсивное определение.
В программировании под рекурсией понимается:
При косвенной рекурсии обязательно использование опережающего объявления с помощью ключевого слова forward:
Простые примеры использования рекурсии
При вызове этой процедуры произойдет рекурсивное зацикливание, т.к. рекурсивный вызов производится безусловно.
Вывод. Чтобы рекурсивного зацикливания не произошло, рекурсивный вызов должен происходить не безусловно, а по какому-то условию, которое всякий раз меняется и при каком-то рекурсивном вызове становится ложным (так называемое условие продолжения рекурсии).
Исправим нашу процедуру в соответствии со сделанным выводом:
При вызове p(0) будет выведено:
Графически, рекурсивные вызовы можно изобразить так:
Процесс последовательных рекурсивных вызовов подпрограммы из самой себя называется рекурсивным спуском.
Процесс возврата из рекурсивных вызовов называется рекурсивным возвратом.
В данном примере числа выводятся на рекурсивном спуске (т.е. в прямом порядке).
Однако, чтобы действия выполнялись в обратном порядке, их нужно вызывать на рекурсивном возврате.
Максимальная глубина рекурсивных вызовов называется глубиной рекурсии.
Текущая глубина называется текущим уровнем рекурсии.
Замечание. Чем больше глубина рекурсии, тем больше накладные расходы по памяти.
Графические изображения рекурсивных вызовов
Одно графическое изображение у нас уже было. Вспомним его:
Рассмотрим более детально вызов p(0) процедуры
Т.о. на стеке фактически хранятся все значения переменной i.
Поэтому следующий код — очень плохой.
Замечание 2. Накладные расходы на помещение на стек ЗА, снятие ЗА со стека, а также присваивание значений формальным параметрам на стеке достаточно велики.
Поэтому если имеется простое нерекурсивное решение (итерационное), то следует использовать именно его.
Замечание 3. Любую рекурсию можно заменить итерацией.
Примеры использования рекурсии
0 \\ 1, & n = 0 \end
Тогда решение имеет вид:
Однако, заметим, что возвращаемое значение не определено для n = 0)). Но его использование при каждом рекурсивном вызове накладно. Поэтому можно «обернуть» рекурсивную подпрограмму, например, так:
Глубина рекурсии этого алгоритма равна n.
Пример 2. Найти 
0 \\ a a^
Глубина рекурсии равна:
Пример 3. Нахождение минимального элемента в массиве. Определить этот элемент можем как минимальный(один элемент, минимальный из массива без этого элемента), т.е. рекурсивное определение следующее:
В соответствии с этим имеем решение:
Ясно, что это не очень хороший результат.
Можно значительно уменьшить глубину, если искать минимальный среди примерно равных частей массива. Т.е. нужно поделить массив пополам, найти в каждой половине минимальные элементы и сравнить их. Поиск в половине осуществляется подобным же образом, и деление производится до тех пор, пока в подмассиве не останется один элемент.
Можно еще немного оптимизировать этот алгоритм — если в подмассиве два элемента, достаточно вернуть минимальный из них.
Теперь знания количества элементов недостаточно: необходимо знать, среди каких элементов массива вести поиск. Поэтому будем в качестве параметров передавать левую (l) и правую (r) границы подмассивов.
Дадим новое рекурсивное определение:
Глубина рекурсии такого алгоритма уже примерно равна 
Пример 4. Вывод односвязного линейного списка на экран.
Вспомним, как выглядит список:
Рекурсия называется концевой, если рекурсивный вызов является последним в подпрограмме.
Концевая рекурсия наиболее легко превращается в итеративный алгоритм:
Доказательство завершимости рекурсии
Добавим к рекурсивной процедуре целый параметр n:
Если при каждом рекурсивном вызове параметр n уменьшается получим вызовы
И если рекурсия завершается при n Формы рекурсивных подпрограмм
1. Действие выполняется на рекурсивном спуске
2. Действие выполняется на рекурсивном возврате
3. Действие выполняется и на рекурсивном спуске и на рекурсивном возврате
4. Каскадная рекурсия
Эта рекурсия называется каскадной, т.к. каждый вызов подпрограммы может порождать несколько рекурсивных вызовов (каскад).
Примером удаленной рекурсии служит функция Аккермана:
0,\; n = 0; \\A(m-1,\;A(m,\;n-1)),& m > 0,\; n > 0.\end
Примеры плохого и хорошего использования рекурсии
Числа Фибоначчи задаются следующим рекуррентным соотношением:
Мы уже вычисляли их с помощью циклов. Возможно рекурсивное (плохое!) решение:
Вот что произойдет при вызове Fib(7):
дерево рекурсивных вызовов
Как видим, одни и те же числа вычисляются по несколько раз:
Алгоритм можно улучшить, использовав массив, первоначально заполненный нулями.
При первом вычислении fib(n) будем заполнять соответствующий элемент, а при всех последующих — просто обращаться к его значению. Подобная методика называется мемоизацией, т.е. запоминанием промежуточных результатов для исключения их повторного вычисления.
Очевидно, данный способ крайне неэффективен по сравнению с итерационным алгоритмом как по памяти, так и по времени работы. В частности, глубина рекурсии при вычислении n-того числа Фибоначчи составляет n-1.
Рекурсивный способ вычисления чисел Фибоначчи, построенный по итерационному алгоритму
Напомним итерационный алгоритм поиска n-того числа Фибоначчи:
Построим по нему рекурсивный алгоритм, передавая в каждую рекурсивную подпрограмму переменные a,b,c, меняющиеся на каждой итерации цикла. Фактически при каждом рекурсивном вызове мы будем совершать подстановку:
Рекурсивный алгоритм, реализованный по этой подстановке, будет иметь вид:
Задача состоит в следующем:
Даны три стержня. На первом лежат n дисков разного радиуса при условии, что ни один диск бОльшего радиуса не лежит на диске мЕньшего радиуса.
Hеобходимо перенести диски с первого стержня на третий, пользуясь вторым, при условии:
Идея алгоритма такая:
Т.о. имеем простое рекурсивное решение:
Быстрая сортировка
Алгоритм
Алгоритм быстрой сортировки (разновидность алгоритма «разделяй и влавствуй») состоит из двух этапов:
1. Выбор некоторого элемента массива x и разделение массива на две части так, что в первой оказываются все элементы = x
2. Рекурсивное применение нашего алгоритма к полученным частям
Очевидно, алгоритм будет работать тем быстрее, чем на более равные части мы будем делить массив (в идеале — каждый раз пополам).
Поэтому мы должны стремиться выбрать элемент x так, чтобы примерно половина элементов массива была =. С другой стороны, выбор x не должен занимать много времени и, по крайней мере, не зависеть от n — размера массива).
Мы будем использовать простейший способ выбора x — в качестве него брать первый элемент.
На следующей анимации представлен пример применения алгоритма быстрой сортировки к массиву
Рассмотрим этап 1 подробнее:
- Для разделения массива на указанные части заведем 2 индекса i и j.
- В начале i будет указывать на первый элемент и двигаться вправо, а j — на последний и двигаться влево.
Шаг 1.
Будем продвигать i вперед до тех пор, пока A[i] не станет >= x.
Далее будем продвигать j назад до тех пор, пока A[j] не станет = j.
В результате получим массив A, разделенный на 2 части:
Код программы
Асимптотическая оценка сложности
Будем исходить из того, что массив всякий раз делится на 2 одинаковые части. Это самый лучший вариант.
Глубина рекурсии в этом случае = log2n.
Очевидно, что в алгоритме Partition мы просматриваем все элементы «своей части» ровно один раз. Т.е. на каждом уровне рекурсии будут по одному разу просмотрены все элементы массива.
Это означает, что асимптотическая сложность Partition на каждом уровне рекурсии = Θ(n).
Т.о., при условии деления примерно пополам, асимптотическая сложность всего алгоритма = Θ(n log n).
Теоретически доказано, что в среднем, если делим не точно пополам, асимптотическая сложность сохраняет формулу Θ(n log n).
Вопрос: какова сложность в худшем случае? Худший — когда в качестве x выбираем минимальный (или максимальный) элемент. Это происходит (в нашей ситуации, т.к. мы выбираем первый элемент), если массив уже отсортирован.
В этом случае в результате разбиения на части большая часть будет уменьшаться на 1, и глубина рекурсии в процедуре Sort будет равна 
Поэтому в худшем случае асимптотическая сложность = 
Утверждение. Для произвольных данных не существует алгоритма с асимптотической сложностью лучше, чем Θ(n log n) в среднем.
Генерация всех перестановок
Основная идея алгоритма генерации всех перестановок заключается в следующем. В массиве длины n, содержащем перестановку, будем менять последний элемент с каждым, после чего будем рекурсивно будем делать то же самое для массива длины n-1 и затем возвращать переставленный элемент на старое место. Если достигнута длина массива n=1, то переставлять ничего не нужно, а следует выдавать содержимое всего массива-перестановки на экран. Такой алгоритм позволит сгенерировать все перестановки, что следует из словесного рекурсивного определения: на последнем месте побывает каждый элемент, содержащийся в рассматриваемом массиве, после чего к оставшейся части массива рекурсивно будет применен тот же алгоритм.
Нетрудно видеть, что глубина рекурсии составляет n-1, а количество вызовов процедуры Perm составляет n!.
Генерация всех подмножеств
Генерация всех подмножеств представляет собой алгоритм перебора. В алгоритмах перебора перебираются все варианты и для подходящих вариантов выполняется определенное действие. В данном случае просто выводятся все подмножества.
Рекурсия и стек
Вернёмся к функциям и изучим их более подробно.
Нашей первой темой будет рекурсия.
Если вы не новичок в программировании, то, возможно, уже знакомы с рекурсией и можете пропустить эту главу.
Рекурсия – это приём программирования, полезный в ситуациях, когда задача может быть естественно разделена на несколько аналогичных, но более простых задач. Или когда задача может быть упрощена до несложных действий плюс простой вариант той же задачи. Или, как мы скоро увидим, для работы с определёнными структурами данных.
В процессе выполнения задачи в теле функции могут быть вызваны другие функции для выполнения подзадач. Частный случай подвызова – когда функция вызывает сама себя. Это как раз и называется рекурсией.
Два способа мышления
Рассмотрим два способа её реализации.
Итеративный способ: цикл for :
Рекурсивный способ: упрощение задачи и вызов функцией самой себя:
Обратите внимание, что рекурсивный вариант отличается принципиально.
Когда функция pow(x, n) вызывается, исполнение делится на две ветви:
Например, рекурсивный вариант вычисления pow(2, 4) состоит из шагов:
Итак, рекурсию используют, когда вычисление функции можно свести к её более простому вызову, а его – к ещё более простому и так далее, пока значение не станет очевидно.
Рекурсивное решение задачи обычно короче, чем итеративное.
Максимальная глубина рекурсии ограничена движком JavaScript. Точно можно рассчитывать на 10000 вложенных вызовов, некоторые интерпретаторы допускают и больше, но для большинства из них 100000 вызовов – за пределами возможностей. Существуют автоматические оптимизации, помогающие избежать переполнения стека вызовов («оптимизация хвостовой рекурсии»), но они ещё не поддерживаются везде и работают только для простых случаев.
Это ограничивает применение рекурсии, но она всё равно широко распространена: для решения большого числа задач рекурсивный способ решения даёт более простой код, который легче поддерживать.
Контекст выполнения, стек
Теперь мы посмотрим, как работают рекурсивные вызовы. Для этого заглянем «под капот» функций.
Информация о процессе выполнения запущенной функции хранится в её контексте выполнения (execution context).
Контекст выполнения – специальная внутренняя структура данных, которая содержит информацию о вызове функции. Она включает в себя конкретное место в коде, на котором находится интерпретатор, локальные переменные функции, значение this (мы не используем его в данном примере) и прочую служебную информацию.
Один вызов функции имеет ровно один контекст выполнения, связанный с ним.
Когда функция производит вложенный вызов, происходит следующее:
pow(2, 3)
Можно схематически изобразить это так:
Это только начало выполнения функции. Условие n == 1 ложно, поэтому выполнение идёт во вторую ветку if :
Значения переменных те же самые, но выполнение функции перешло к другой строке, актуальный контекст:
pow(2, 2)
Для выполнения вложенного вызова JavaScript запоминает текущий контекст выполнения в стеке контекстов выполнения.
Вид контекста в начале выполнения вложенного вызова pow(2, 2) :
Новый контекст выполнения находится на вершине стека (и выделен жирным), а предыдущие запомненные контексты – под ним.
Когда выполнение подвызова закончится, можно будет легко вернуться назад, потому что контекст сохраняет как переменные, так и точное место кода, в котором он остановился. Слово «строка» на рисунках условно, на самом деле запоминается более точное место в цепочке команд.
pow(2, 1)
Создаётся новый контекст выполнения, предыдущий контекст добавляется в стек:
Выход
Когда функция заканчивается, контекст её выполнения больше не нужен, поэтому он удаляется из памяти, а из стека восстанавливается предыдущий:
Восстанавливается контекст предыдущего вызова:
Глубина рекурсии в данном случае составила 3.
Как видно из иллюстраций выше, глубина рекурсии равна максимальному числу контекстов, одновременно хранимых в стеке.
Обратим внимание на требования к памяти. Рекурсия приводит к хранению всех данных для неоконченных внешних вызовов в стеке, и в данном случае это приводит к тому, что возведение в степень n хранит в памяти n различных контекстов.
Реализация возведения в степень через цикл гораздо более экономна:
Любая рекурсия может быть переделана в цикл. Как правило, вариант с циклом будет эффективнее.
Но переделка рекурсии в цикл может быть нетривиальной, особенно когда в функции в зависимости от условий используются различные рекурсивные подвызовы, результаты которых объединяются, или когда ветвление более сложное. Оптимизация может быть ненужной и совершенно нестоящей усилий.
Часто код с использованием рекурсии более короткий, лёгкий для понимания и поддержки. Оптимизация требуется не везде, как правило, нам важен хороший код, поэтому она и используется.
Рекурсивные обходы
Другим отличным применением рекурсии является рекурсивный обход.
Представьте, у нас есть компания. Структура персонала может быть представлена как объект:
Другими словами, в компании есть отделы.
Отдел может состоять из массива работников. Например, в отделе sales работают 2 сотрудника: Джон и Алиса.
Также возможно, что при росте подотдела он делится на подразделения (или команды).
Теперь, допустим, нам нужна функция для получения суммы всех зарплат. Как мы можем это сделать?
Итеративный подход не прост, потому что структура довольно сложная. Первая идея заключается в том, чтобы сделать цикл for поверх объекта company с вложенным циклом над отделами 1-го уровня вложенности. Но затем нам нужно больше вложенных циклов для итераций над сотрудниками отделов второго уровня, таких как sites … А затем ещё один цикл по отделам 3-го уровня, которые могут появиться в будущем? Если мы поместим в код 3-4 вложенных цикла для обхода одного объекта, то это будет довольно некрасиво.
Давайте попробуем рекурсию.
Как мы видим, когда наша функция получает отдел для подсчёта суммы зарплат, есть два возможных случая:
Случай (1), когда мы получили массив, является базой рекурсии, тривиальным случаем.
Случай (2), при получении объекта, является шагом рекурсии. Сложная задача разделяется на подзадачи для подотделов. Они могут, в свою очередь, снова разделиться на подотделы, но рано или поздно это разделение закончится, и решение сведётся к случаю (1).
Рекурсия. Рекурсивные подпрограммы.
По известному вам правилу доступности переменных (объектов), в теле подпрограммы доступны все переменные (объекты), объявленные в самой подпрограмме, а также переменные (объекты) объявленные во всех объемлющих блоках, в том числе и имя самой подпрограммы. Исключение составляет случай, когда переменная (объект) имеет такое-же имя как и переменная в объемлющем блоке и экранирует собой глобальную переменную.
Следствием правила о доступности переменных (объектов) является возможность вызова подпрограммой самой себя.
Процедуры и функции, производящие вызов "самих себя" называют рекурсивными.
Рекурсия. Рекурсивный алгоритм.
Рекурсией называется ситуация, когда какая-то подпрограмма прямо или через другие подпрограммы вызывает себя в качестве подпрограммы. Реализуемый при этом алгоритм называется рекурсивным.
В математике очень часто встречаются последовательности чисел, в которых каждый следующий член выражается через предыдущие. В арифметической прогрессии, например, каждый следующий член равен предыдущему, увеличенному на разность прогрессии:
Формулы, выражающие очередной член последовательности через один или несколько предыдущих членов, называют рекуррентными соотношениями.
Рассмотрим для примера функцию вычисления факториала n!. Как правило ее определяют как правило произведения первых n чисел натурального ряда
Такое произведение можно легко вычислить с помощью итеративных конструкций (итерация ― это повторение), например, оператор цикла For
Procedure TForm1.Button1Click(Sender: TObject);
n:=StrToInt(Edit1.Text); // Вводим n для вычисления n!
For i:=1 to n do fact:=Fact*i;
Label1.Caption:='Факториал ' +IntToStr(n)+'! ='+IntToStr(fact);
Однако существует другое определение факториала, в котором n! выражается через предыдущий (n-1)!, т.е. используется рекуррентная формула:
Наличие рекуррентного соотношения позволяет использовать рекурсию. Например, программа, использующая рекурсивную функцию для вычисления факториала n! имеет следующий вид:
Label1.Caption:=' Факториал '+IntToStr(n)+'! ='+IntToStr(fact(n));
Чтобы понять, как она работает, вспомним, что на время выполнения подпрограммы вызывающая подпрограмма приостанавливается, а в оперативной памяти выделяется место для локальных переменных и параметров, вызванной подпрограммы. Таким образом, при вызовах подпрограмм в оперативной памяти "накапливаются" приостановленные программы. При рекурсивных вызовах одной и той же функции fact происходит то же самое, т.е. при каждом новом вызове функции fact для ее локальных переменных и параметров выделяются новые ячейки памяти. по завершению работы функции эти ячейки удаляются.
Программы, в которых используются рекурсивные подпрограммы отличаются простотой, наглядностью и компактностью кода. Однако за эту простату приходится расплачиваться неэкономным использованием оперативной памяти, так как выполнение рекурсивных подпрограмм требует значительно большего размера оперативной памяти во время выполнения, чем нерекурсивных. При каждом рекурсивном вызове для локальных переменных, а также для параметров подпрограмм, которые передаются по значению, выделяются новые ячейки памяти в программном стеке.
В Delphi нет никаких ограничений на рекурсивные вызовы подпрограмм, необходимо только хорошо понимать, что каждый очередной рекурсивный вызов приводит к образованию новой копии локальных объектов подпрограммы и все эти копии, соответствующие цепочки активизированных и не завершенных рекурсивных вызовов, существуют независимо друг от друга.
Для рассмотрения различных форм рекурсивных подпрограмм введем некоторые определения, имеющие отношение к рекурсии.
Максимальное число рекурсивных вызовов подпрограммы без возвратов, которое происходит во время выполнения программы, называется глубиной рекурсии.
Текущий уровень рекурсии.
Число рекурсивных вызовов в каждый конкретный момент времени, называется текущим уровнем рекурсии.
Формы рекурсивных подпрограмм.
В общем случае любая рекурсивная подпрограмма (для примера назовем ее Rec) включает в себя некоторое множество операторов S и один или несколько операторов рекурсивного вызова P.
Главное требование к рекурсивным подпрограммам.
Главное требование к рекурсивным подпрограммам заключается в том, что вызов рекурсивной подпрограммы должен выполняться по условию, которое на каком-то уровне рекурсии станет ложным. Если условие истинно, то рекурсивный спуск продолжается. Когда оно становится ложным, то спуск заканчивается и начинается рекурсивный возврат из всех вызванных на данный момент копий рекурсивной подпрограммы.
Существует три разных формы рекурсивных подпрограмм:
1) Форма с выполнением действий до рекурсивного вызова (с выполнением действий на рекурсивном спуске).
If условие > then Rec;
2) Форма с выполнением действий после рекурсивного вызова (с выполнением действий на рекурсивном возврате).
If условие > then Rec;
3) Форма с выполнением действий как до, так и после рекурсивного вызова (с выполнением действий как на рекурсивном спуске, так и на рекурсивном возврате).
If условие > then Rec;
Все формы рекурсивных процедур находят применение на практике. Многие задачи, в том числе вычисление факториала, безразличны к тому, какая используется форма рекурсивной процедуры.
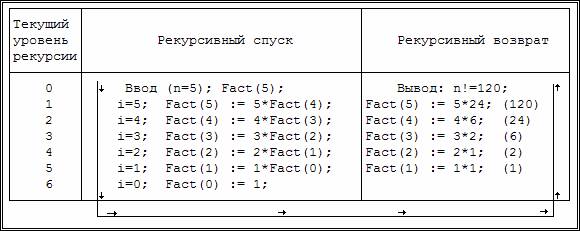
Рассмотренная в начале рекурсивная функция fact, выполняет вычисление факториала на возврате. Рассмотрим более подробно действия этой функции при вычислении 5!, используя трассировку программы (запись значений переменных на различных этапах выполнения программы).
В качестве примера мы использовали рекурсивную функцию вычисления факториала натурального числа. Может показаться, что составить программу для вычисления n! используя прямую формулу значительно проще, чем составить программу на основе рекуррентного соотношения. Но в подавляющем большинстве случаев это не так. В качестве второго примера рассмотрим программу для вычисления члена последовательности Фибоначчи, для которого рекуррентное соотношение
для любого n>2 F(n)=F(n-1)+F(n-2)
выглядит значительно проще, чем прямая формула
используя которую составить программу практически невозможно. Приведем функцию, благодаря которой можно быстро рассчитать эти числа:
If (i=1) or (i=2) then fib:=1
Рекурсивный вызов может быть косвенным. В этом случае подпрограмма обращается к себе опосредованно, путем вызова другой подпрограммы, в которой содержится обращение к первой, например:
Procedure A (i : Byte);
Procedure В (j : Byte) ;
Если строго следовать правилу, согласно которому каждый идентификатор перед употреблением должен быть описан, то такую программную конструкцию использовать нельзя. Чтобы такого рода вызовы стали возможны, вводится опережающее описание:
Procedure В (j : Byte); Forward;
Procedure A (i : Byte);
Как видим, опережающее описание заключается в том, что объявляется лишь заголовок процедуры в, а ее тело заменяется стандартной директивой Forward. Теперь в процедуре А можно использовать обращение к процедуре В ― ведь она уже описана, точнее, известны ее формальные параметры, и компилятор может правильным образом организовать ее вызов. Обратите внимание: тело процедуры В начинается заголовком, в котором уже не указываются описанные ранее формальные параметры.
Пример использования рекурсивной подпрограммы:
Задача: пара кроликов приносит раз в месяц приплод из двух крольчат (самца и самки), причем новорожденные крольчата через два месяца после рождения уже приносят приплод. Сколько пар кроликов появится через год, если в начале года была одна пара кроликов и в течение года кролики не умирают, а их воспроизводство не заканчивается?
Procedure recursya(i:Int64; Var kol1:Int64; Var kol2:Int64);
kol1:=1; //первоначальное количество пар кроликов
kol2:=2; //количество пар кроликов через месяц
i:=i-1; // рекурсивный спуск
Procedure TForm1.Button1Click(Sender: TObject);
1. Что такое рекурсия?
2. Какие соотношения называют рекуррентными?
3. В чем заключаются преимущества и недостатки в использовании рекурсивных подпрограмм по сравнению с нерекурсивными?
4. Что называется глубиной рекурсии?
5. Что называется текущим уровнем рекурсии?
6. Сформулируйте основные требования к рекурсивным подпрограммам.
7. Назовите формы рекурсивных подпрограмм.
8. Что называют рекурсивным спуском и возвратом?