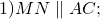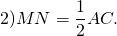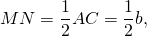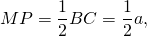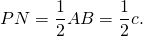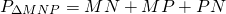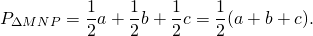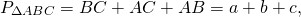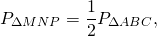что делает средняя линия в треугольнике с площадью

Средняя линия треугольника

Определение 1. Средней линией треугольника называется отрезок, соединяющий середины двух сторон.

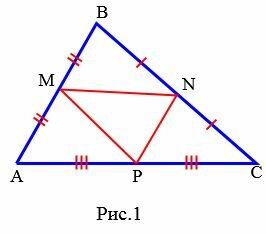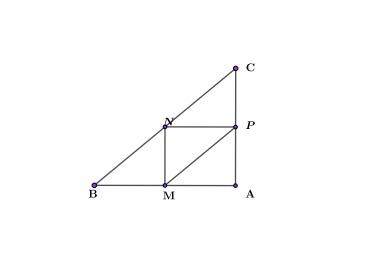
У треугольника три средние линии. На Рис.1 отрезки MN, NP, MP являются средними линиями треугольника.

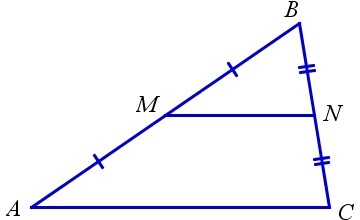
Теорема 1. Средняя линия треугольника, соединяющая середины двух его сторон параллельна третьей стороне и равна ее половине.

Доказательство. Пусть MN средняя линия треугольника ABC (Рис.2). Докажем, что \( \small MN || AC, \) \( \small MN=\frac12 AC. \)

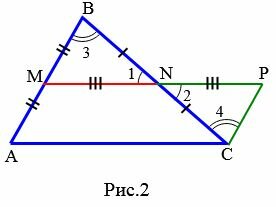Далее, поскольку точка M является серединой отрезка AB, имеем : AM=MB. Но \( \small MB=CP \) и, следовательно AM = CP. Получили что в четырехугольнике AMPC стороны AM и CP параллельны и равны. Тогда по признаку 1 статьи Параллелограмм четырехугольник AMPC является параллелограммом. Отсюда следует, что MP || AC или MN ||AC.

Остается показать, что \( \small MN=\frac12 AC. \) Так как MN=NP, то \( \small MN=\frac12 MP. \) Но в параллелограмме MP = AC. Тогда \( \small MN=\frac12 AC. \)

Источник

Средняя линия треугольника

Теорема

Доказательство

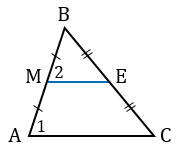
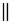
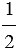
Доказать: МЕАС, МЕ = АС.

Доказательство:

В треугольниках МВЕ и АВС:

Следовательно, треугольники МВЕ и АВС подобны (по 2 признаку подобия треугольников), поэтому 1 =2 и .

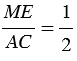
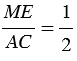
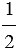
Из равенства следует, что МЕ = АС. Теорема доказана.

Задача:

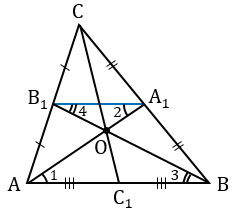
Доказать, что медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины.

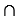
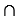
Доказать: АА₁ВВ₁СС₁ = О, АО : ОА₁ = ВО : ОВ₁ = СО : ОС₁ = 2 : 1.

Доказательство:

. (1)

.

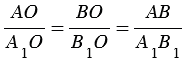
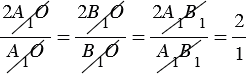
Следовательно, точка О, в которой пересекаются медианы АА₁ и ВВ₁ делит каждую из них в отношении 2 : 1, считая от вершины.

Аналогично доказывается, что точка пересечения медиан ВВ₁ и СС₁ делит каждую из них в отношении 2 : 1, считая от вершины, и, значит, совпадает с точкой О.

Итак, все три медианы АВС пересекаются в точке О и делятся ею в отношении 2 : 1, считая от вершины. Что и требовалось доказать.

Поделись с друзьями в социальных сетях:

Источник

Как найти среднюю линию треугольника

​Средняя линия треугольника — отрезок, соединяющий середины двух его сторон.

Свойства и признаки

Признак средней линии: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей, то этот отрезок называется средней линией данного треугольника.

Свойства:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Формула для расчета

Теорема

Средняя линия треугольника параллельна основанию и равна её половине.

Доказательство

Рассмотрим \(\triangle BA_1C_1\) и \(\triangle BAC\) :

Из этого следует, что треугольники подобны по двум пропорциональным сторонам и углу между ними.

Кроме того, из подобия следует, что \(\frac=\frac12\)

Примечание

Данная формула одинаково работает для любого треугольника: равнобедренного, равностороннего (правильного).

Задачи на использование теоремы

Задача 1

В прямоугольном треугольнике ABC проведены средние линии: MN; NP; MP. При этом MN=NP=2. Найти площадь треугольника ABC.

Рассмотрим прямоугольный треугольник NMP:

\(S_<\triangle NMP>=\frac12\times MN\times NP=\frac12\times2\times2=2\)

Все маленькие треугольники равны, следовательно \(S_<\triangle ABC>=2\times4=8\)

Задача 2

Площадь треугольника ABC равна 8. MN — средняя линия. Необходимо вычислить площадь треугольника BMN.

Задача 3

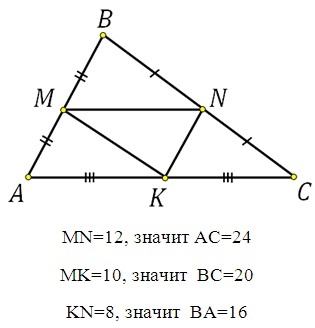
В треугольнике ABC точки M, N, K – середины сторон AB, BC, AC соответственно, MN=12, MK=10, KN=8. Необходимо узнать периметр треугольника ABC.

Средняя линия равна половине основания, следовательно находим:

Источник

Средняя линия треугольника

Что такое средняя линия треугольника?

Каковы свойства средней линии треугольника?

Сколько средних линий в треугольнике?

Средняя линия треугольника — это отрезок, соединяющий середины двух его сторон.

M — середина AB,

MN — средняя линия треугольника ABC.

Поскольку в треугольнике три стороны, треугольник имеет три средние линии.

MN, MP, PN — средние линии треугольника ABC.

Теорема (Свойства средней линии треугольника).

Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине:

Стороны треугольника равны a, b, c. Найти стороны и периметр треугольника, вершинами которого являются середины сторон данного треугольника.

Дано: ∆ ABC, AB=c, BC=a, AC=b,

M — середина AB, N — середина BC,

Найти: MN, PN, MP, P(∆ ABC).

Так как точки M, N и P являются серединами сторон треугольника ABC, то отрезки MN, PN и MP- средние линии этого треугольника (по определению).

По свойству средней линии треугольника

то есть периметр треугольника, вершинами которого являются середины сторон данного треугольника, равен половине периметра данного треугольника.

Источник

Средняя линия треугольника

Определения

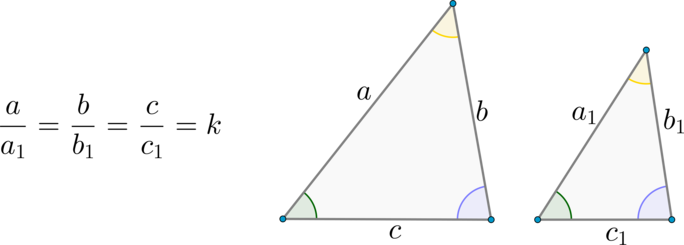
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого
(стороны называются сходственными, если они лежат напротив равных углов).

Коэффициент подобия (подобных) треугольников – это число, равное отношению сходственных сторон этих треугольников.

Определение

Периметр треугольника – это сумма длин всех его сторон.

Теорема

Отношение периметров двух подобных треугольников равно коэффициенту подобия.

Доказательство

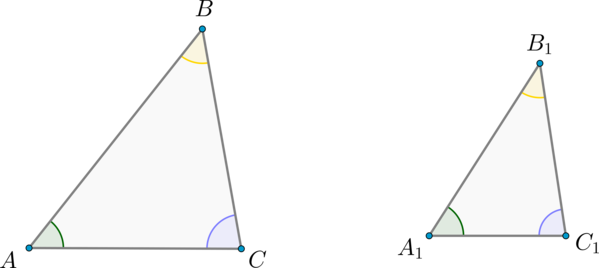
Рассмотрим треугольники \(ABC\) и \(A_1B_1C_1\) со сторонами \(a,b,c\) и \(a_1, b_1, c_1\) соответственно (см. рисунок выше).

Тогда \(P_=a+b+c=ka_1+kb_1+kc_1=k(a_1+b_1+c_1)=k\cdot P_\)

Теорема

Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

Доказательство

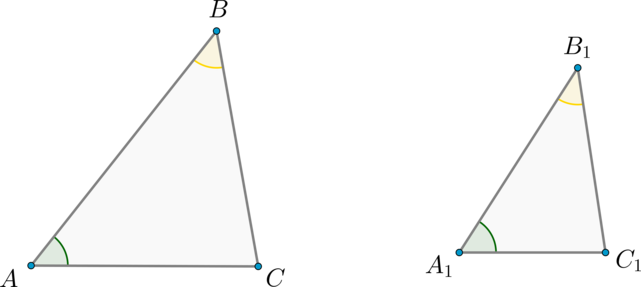
Теорема (первый признак подобия треугольников)

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

Доказательство

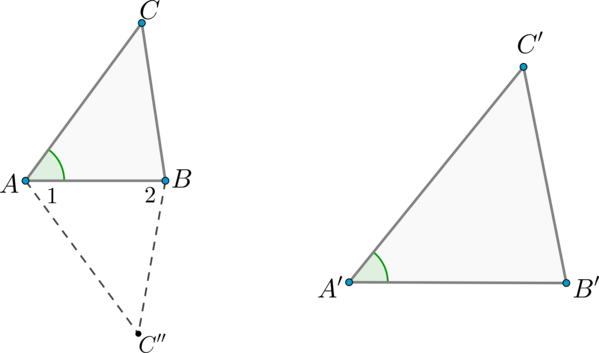
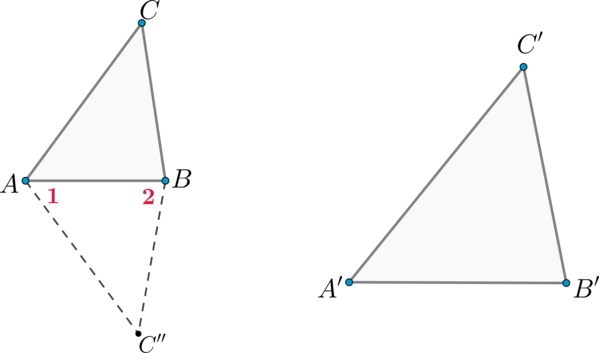
Теорема (второй признак подобия треугольников)

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

Доказательство

Теорема (третий признак подобия треугольников)

Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

Доказательство

Теорема

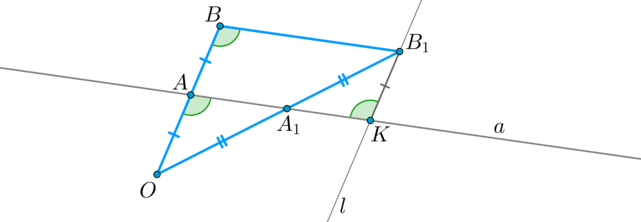
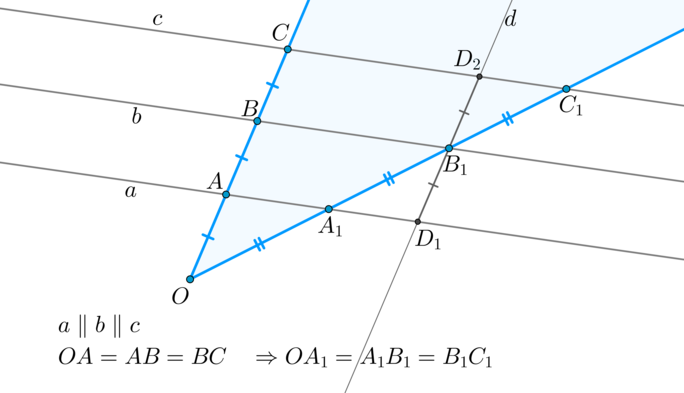
Если на одной из сторон угла отметить равные между собой отрезки и через их концы провести параллельные прямые, то эти прямые отсекут на второй стороне также равные между собой отрезки.

Доказательство

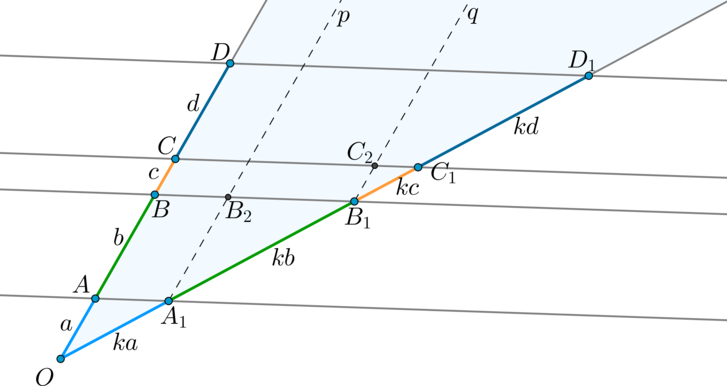
Теорема Фалеса

Параллельные прямые отсекают на сторонах угла пропорциональные отрезки.

Доказательство

Аналогично проведем через \(B_1\) прямую \(q\parallel OD \Rightarrow \triangle OBB_1\sim \triangle B_1C_1C_2 \Rightarrow B_1C_1=kc\) и т.д.

Определение

Средняя линия треугольника – это отрезок, соединяющий середины любых двух сторон треугольника.

Теорема

Средняя линия треугольника параллельна третьей стороне и равна ее половине.

Доказательство

1) Параллельность средней линию основанию следует из доказанной выше леммы.

Следствие

Источник