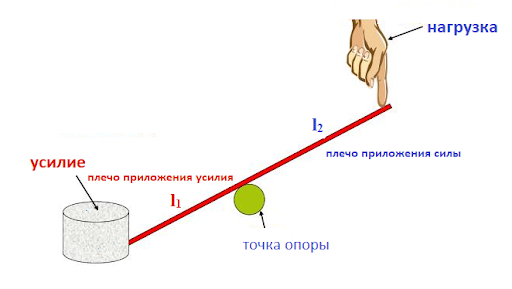
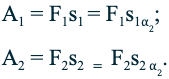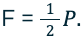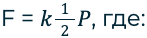что дает выигрыш в силе
Простые механизмы. «Золотое правило» механики
п.1. Виды простых механизмов
По традиции, сложившейся ещё со времен Возрождения, к простым механизмам относятся:
Примеры физических систем в механике
п.2. Принцип действия рычага
Подробно рычаги и условия равновесия были рассмотрены в §26 данного справочника.
В этом разделе мы рассмотрим принцип работы рычага с точки зрения закона сохранения энергии.
Пусть действие приложенной силы \(F_1\) приводит к перемещению \(h_1\) левого плеча вниз.
Работа приложенной силы равна \(A_1=F_1h_1\).
Тогда правое плечо при этом переместится вверх на расстояние \(h_2\).
Получаем, что \(F_1h_1=F_2h_2\).
Что соответствует результату, полученному ранее.
п.3. «Золотое правило» механики
 | Архимеду приписывают следующую фразу: «Дайте мне точку опоры, и я переверну Землю». |
Попробуем для начала хотя бы сдвинуть Землю на 1 микрон с орбиты, \(h_2=1\ \text<мкм>=10^<-6>\ \text<м>\). Это послужит хорошей иллюстрацией «золотого ПРАВИЛО» механики.
Расстояние от Солнца до Земли – 1 астрономическая единица – это «всего лишь» 150 миллионов километров:\(1\ \text<а.е.>\approx 1,5\cdot 10^<11>\ \text<(м)>\).
Значит, если на одной стороне рычага мы сдвигаем Землю на 1 микрон, то на другой стороне – прикладывая весь свой вес – должны преодолеть расстояние в полторы Солнечных системы. Вот что такое – «проигрыш в расстоянии».
п.4. Блоки и полиспасты
Блок — это колесо с желобом, по которому пропущена веревка или трос.
В технике используют неподвижные и подвижные блоки.
Подвижный блок даёт выигрыш в силе в 2 раза.
При этом получаем двойной проигрыш в расстоянии: чтобы поднять груз на высоту \(h\), нужно вытравить канат справа на длину \(2h\).
В реальных ситуациях выигрыш в силе при использовании подвижного блока получается меньшим, т.к. часть работы уходит на подъем самой веревки и блока (они тоже имеют вес) и преодоление трения.
На практике используют комбинации из неподвижных и подвижных блоков – полиспасты.
Они позволяют получить выигрыш в силе и менять её направление.
Чем больше в полиспасте подвижных блоков, тем большим будет выигрыш в силе.
Характеристики полиспастов представлены в таблице.
| № | К-во неподвижных блоков | К-во подвижных блоков | Изменение направления силы, раз | Выигрыш в силе, раз | Проигрыш в расстоянии, раз |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 2 | 1 | 1 | 1 | 2 | 2 |
| 3 | 1 | 2 | 1 | 3 | 3 |
| 4 | 1 | 3 | 1 | 4 | 4 |
| 5 | 1 | 4 | 1 | 5 | 5 |
| 6 | 1 | 5 | 1 | 6 | 6 |
п.5. «Золотое правило» механики для гидравлического пресса
Подробней о гидравлическом прессе – см. §30 данного справочника.
Работы малого и большого поршня равны.
Таким образом, «золотое правило» для гидравлического пресса также выполняется.
Гидравлический пресс не дает выигрыша в работе.
п.6. «Золотое правило» механики для наклонной плоскости
В любом случае тело, оказавшись в точке B, приобретает потенциальную энергию \begin
Получаем \begin
Наклонная плоскость не дает выигрыша в работе.
Выигрыш в силе компенсируется проигрышем в расстоянии.
Выигрыш в силе равен отношению длины наклонной плоскости к высоте.
Например, из пяти наклонных плоскостей, представленных на рисунке, наибольший выигрыш в силе даст плоскость 5, т.к. у нее отношение \(\frac Lh\) максимально (угол наклона минимален).
В реальности, если учесть силу трения, этот выигрыш уменьшается, т.к. с уменьшением угла наклона сила трения растет.
п.7. Задачи
Задача 1. Груз весом 200 Н равномерно поднимают по наклонной плоскости на высоту 5 м, прикладывая силу 100 Н. Найдите длину наклонной плоскости. Трением можно пренебречь.
Работы при подъеме тела вверх и при перемещении вдоль наклонной плоскости равны: \(A=Ph=FL\). Получаем \begin
Задача 2. При штамповке детали больший поршень гидравлического пресса поднялся на 1 см, а меньший поршень опустился на 20 см. Какая сила действовала на деталь, если на малый поршень действовала сила 500 Н.
Работы по перемещению поршней равны: \begin
Задача 3. К концам рычага длиной 1 м подвешены грузы массой 8 кг и 12 кг. На каком расстоянии от середины рычага должна быть точка опоры, чтобы рычаг находился в равновесии? Ответ запишите в сантиметрах.
Плечо для груза 1: \begin
Задача 4. Если груз лежит на левой чашке неравноплечих весов, его уравновешивают гири массой \(m_1=2\ \text<кг>\) на правой чашке. Если же груз положить на правую чашку, его уравновесит только одна гиря массой \(m_2=0,5\ \text<кг>\) на левой чашке. Какова масса \(m\) груза? Во сколько раз одно плечо весов длиннее другого?
Пусть длина правого плеча \(L_1\), левого плеча – \(L_2\).
По условию задачи \begin
Ответ: 1 кг; левое плечо длиннее правого в 2 раза
Задача 5*. Прямолинейный кусок проволоки массой \(m=40\ \text<г>\) подвешен за середину. Левую половину куска согнули, как показано на рисунке. Какой массы груз надо подвесить в точке A, чтобы восстановить равновесие.
Пусть длина всей проволоки \(L\).
Тогда расстояние от центра тяжести проволоки слева до точки подвеса \(OK=L/4\), а расстояние от центра тяжести проволоки справа до точки подвеса \(OE=L/2\).
Груз массой \(M\) подвешен на расстоянии \(OA=L/2\).
Из ПРАВИЛА моментов получаем: \begin
Сокращаем на \(gL\) \begin
Задача 6*. Балка массой 1200 кг и длиной 3 м лежит на опорах, равноудаленных от ее концов. Расстояние между опорами 2 м.
Какую силу, перпендикулярную балке и направленную вертикально вверх нужно приложить, чтобы приподнять балку за один из её краёв?
Простые механизмы. Блок.
Одним из простых механизмов является блок. Блок — это колесо с желобом, по которому пропущена веревка или трос. Используется блок, как и все простые механизмы, для преобразования силы — т.е. изменения направления и модуля приложенной силы.
Блоки бывают подвижные и неподвижные. Рассмотрим каждый случай подробно.
Неподвижный блок.
Неподвижный блок — это блок, ось которого (точка О на рисунке) закреплена, и блок при подъеме грузов не опускается и не поднимается.
Такой блок можно рассматривать как рычаг первого рода, у которого оба плеча равны между собой, и равны радиусу колеса блока:
Так как плечи рычага равны, то мы не получим выигрыша в силе. Проверим это, используя формулу равновесия рычага:
В нашем случае неподвижного блока:
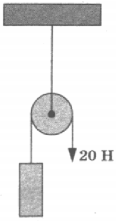
Действительно, для того чтобы уравновесить силу на одном конце веревки, перекинутой через блок, нам необходимо приложить такую же силу на другом конце. Поэтому неподвижные блоки используют в том случае, если удобнее изменить направление силы, для совершения работы. Например, удобнее поднимать груз, удерживая веревку при помощи своего веса, поэтому на рисунке экспериментатор использует неподвижный блок.
Используя комбинации из неподвижных блоков можно менять направление силы как угодно:
И в этом случае, используя уже два неподвижных блока — мы не получаем выигрыша в силе, зато изменили направление приложения силы, теперь для поднятия груза силу мы должны приложить в горизонтальном направлении.
Подвижный блок
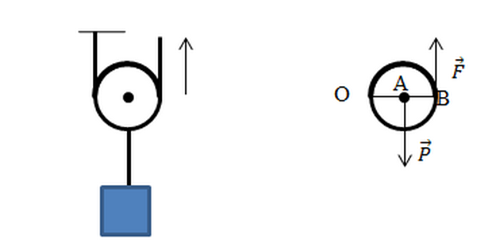
Подвижный блок — это блок, ось которого не закреплена, а поднимается вместе с грузом. Изобразим подвижный блок находящийся в равновесии, отметим на рисунке силы, действующие на систему, а также плечи приложения этих сил:
Подвижный блок можно сравнить с рычагом второго рода. Действительно: точка опоры О лежит по одну сторону от точки приложения сил, отрезок ОА — плечо силы P
Расчет выигрыша в силе: формула, примеры расчета с пояснениями
Содержание:
Рассмотрим, как рассчитать выигрыш в силе при использовании простейших механизмов, которые люди тысячелетиями используют для перемещения тяжёлых предметов: рычаги, наклонные поверхности, блоки. Первые применяются для перемещения массивных предметов с применением сил, которые имеют меньший за них вес; вторые – облегчают передвижение и подъём тел.
О простейших механизмах
Части рычага до и после точки опоры называются плечами:
Механизм создаёт большее физическое усилие на коротком плече, чем сила, прилагаемая к длинному. На практике в его качестве применяются длинные (до нескольких метров) жёсткие деревянные балки, брус, металлические трубы.
Он же стал прообразом первых механических весов.
Рычаг будет находиться в равновесии до момента, пока вращающий его по часовой стрелке момент сил равняется силе, вращающей его в обратном направлении (по модулю). Если у механизма разные оси вращения – расстояние от точки опоры до места прикладывания усилия, такой рычаг даёт выигрыш в силе, расчёт которого проводится по формуле:
В данном случае l1
Действительно, жёсткий рычаг с отличающейся в десятки раз длиной плеч сведёт к минимуму прикладываемую для передвижения либо подъёма предмета силу, но выигрыш в работе он не обеспечит. Во сколько раз легче будет подъем, ровно на столько вещь придётся переместить дальше, а значит выигрыша в работе не получить. Докажем это.
Выполняемая работа пропорциональна прикладываемой силе, пройденному телами расстоянию на угол поворота.
Отсюда выплывает, что энергия в системе ниоткуда не появляется и бесследно не исчезает, только переходит из одной формы в иную. Часть – уходит на нагрев тел вследствие их трения.
Примеры рычага: плоскогубцы, ножницы, клещи, ручной тормоз авто.
Какой выигрыш в силе дает подвижный блок
Различают неподвижные и подвижные блоки – колёса с продольными канавами для верёвки, крепящиеся на ось. Первые изменяют направление воздействия приложенной силы, не предоставляя преимуществ для перемещения вещей, вторые – прикладываемую силу. Подвижной блок перемещается с грузом, уменьшая прикладываемое для движения груза усилие.
Разберёмся, как найти выигрыш в силе в такой ситуации. Поднимая груз весом P посредством подвижного блока, нужно приложить вдвое меньшую силу, чем через неподвижный, ведь плечо OA (радиус) для силы P вдвое меньше OB (диаметра круга) для силы натяжения троса. Если тот вытягивается на длину l, груз поднимается только на половину этого расстояния l2:
С учётом силы трения формула расчета выигрыша в силе приобретает вид:
K – коэффициент трения.
Задача
Рабочий посредством подвижного блока поднимает ведро песка на высоту 6 м. При этом прилагается сила, равная 160 Н. Трение повышает прикладываемую силу на 10%. Рассчитать совершаемую человеком работу?
A = kFs=1,1*160*6= 1056 Дж 1,056 кДж.
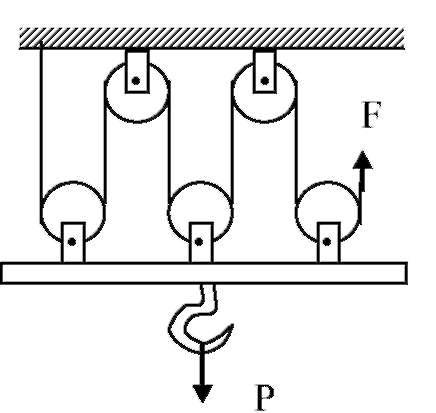
Какой выигрыш в силе даcт использование показанной на рисунке схемы?
Механизм представлен парой неподвижных и тремя подвижными блоками. Каждый снижает прикладываемую силу вдвое, даёт выигрыш в шесть раз.
Простые механизмы.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: простые механизмы, КПД механизма.
Рычаг.
 |
| Рис. 1. Рычаг |
Из этого соотношения следует, что рычаг даёт выигрыш в силе или в расстоянии (смотря по тому, с какой целью он используется) во столько раз, во сколько большее плечо длиннее меньшего.
Например, чтобы усилием 100 Н поднять груз весом 700 Н, нужно взять рычаг с отношением плеч 7 : 1 и положить груз на короткое плечо. Мы выиграем в силе в 7 раз, но во столько же раз проиграем в расстоянии: конец длинного плеча опишет в 7 раз большую дугу, чем конец короткого плеча (то есть груз).
Неподвижный блок.
Важной разновидностью рычага является блок — укреплённое в обойме колесо с жёлобом, по которому пропущена верёвка. В большинстве задач верёвка считается невесомой нерастяжимой нитью.
На рис. 2 изображён неподвижный блок, т. е. блок с неподвижной осью вращения (проходящей перпендикулярно плоскости рисунка через точку ).
 |
Зачем же тогда вообще нужен неподвижный блок? Он полезен тем, что позволяет изменить направление усилия. Обычно неподвижный блок используется как часть более сложных механизмов.
Подвижный блок.
 |
Следовательно, подвижный блок даёт выигрыш в силе в два раза. При этом, однако, мы в те же два раза проигрываем в расстоянии: чтобы поднять груз на один метр, точку придётся переместить на два метра (то есть вытянуть два метра нити).
 |
Принципиально данное устройство ничем не отличается от подвижного блока: с его помощью мы также получаем двукратный выигрыш в силе.
Наклонная плоскость.
Как мы знаем, тяжёлую бочку проще вкатить по наклонным мосткам, чем поднимать вертикально. Мостки, таким образом, являются механизмом, который даёт выигрыш в силе.
 |
Выберем ось так, как показано на рисунке. Поскольку груз движется без ускорения, действующие на него силы уравновешены:
Проектируем на ось :
Именно такую силу нужно приложить, что двигать груз вверх по наклонной плоскости.
Широко применяемыми разновидностями наклонной плоскости являются клин и винт.
Золотое правило механики.
Простой механизм может дать выигрыш в силе или в расстоянии, но не может дать выигрыша в работе.
т. е. той же величине, что и без использования рычага.
т. е. ту же самую, что и при вертикальном поднятии груза.
Данные факты служат проявлениями так называемого золотого правила механики.
Золотое правило механики. Ни один из простых механизмов не даёт выигрыша в работе. Во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии, и наоборот.
Золотое правило механики есть не что иное, как простой вариант закона сохранения энергии.
КПД механизма.
На практике приходится различать полезную работу A полезн, которую нужно совершить при помощи механизма в идеальных условиях отсутствия каких-либо потерь, и полную работу Aполн,
которая совершается для тех же целей в реальной ситуации.
Полная работа равна сумме:
-полезной работы;
-работы, совершённой против сил трения в различных частях механизма;
-работы, совершённой по перемещению составных элементов механизма.
Так, при подъёме груза рычагом приходится вдобавок совершать работу по преодолению силы трения в оси рычага и по перемещению самого рычага, имеющего некоторый вес.
Полная работа всегда больше полезной. Отношение полезной работы к полной называется коэффициентом полезного действия (КПД) механизма:
КПД принято выражать в процентах. КПД реальных механизмов всегда меньше 100%.
 |
Ускорения нет, поэтому силы, действующие на груз, уравновешены:
Проектируем на ось X:
Проектируем на ось Y:
Полная работа равна произведению силы F на путь, пройденный телом вдоль поверхности наклонной плоскости:
Простые механизмы. КПД простых механизмов
1. Простые механизмы — приспособления, которые сконструировал и использовал человек, чтобы облегчить работу по перемещению тяжёлых предметов. К ним относят: рычаг, блок, наклонную плоскость. Разновидностями этих механизмов являются: клин, ворот и винт.
Все простые механизмы позволяют преобразовать силу, действующую на тело: либо уменьшить её, либо изменить её направление.
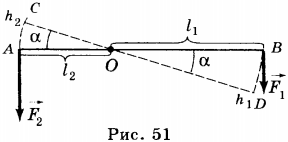
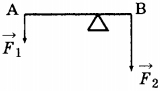
2. Рычаг — это стержень, вращающийся вокруг неподвижной опоры или оси (рис. 51). На рисунке показан рычаг, который может вращаться вокруг точки О, расположенный между концами рычага. К одному концу рычага подвешен груз, действующий на рычаг с силой \( F_1 \) , равной весу груза. Действуя на длинный конец рычага с силой \( F_2 \) , человек поднимает груз. При этом сила \( F_1 \) стремится повернуть рычаг по часовой стрелке, а груз \( F_2 \) — против часовой стрелки.
Из эксперимента следует, что рычаг находится в равновесии, если произведение силы, вращающей рычаг по часовой стрелке, и её плеча равно произведению силы, вращающей рычаг против часовой стрелки, и её плеча, т.е. \( F_1l_1=F_2l_2 \) . Произведение силы, действующей на рычаг, и её плеча называют моментом силы: \( Fl=M \) . Соответственно, если рычаг находится в равновесии, то \( M_1=M_2 \) .
Условие равновесия рычага можно записать по-другому: \( \frac
Рычаг другого типа вращается вокруг точки, находящейся на конце рычага. Примером такого рычага может служить тачка. Когда используется такой рычаг, то вес груза направлен вниз, а человек действует на свободный конец рычага с силой, направленной вверх. Для такого рычага также справедливо условие равновесия, приведенное выше.
4. Ещё одним простым механизмом является блок. Блок — это колесо с желобом, по которому пропускается трос и которое может вращаться относительно оси О (см. рис. ниже).
Если ось блока закреплена, то блок не перемещается, и он называется неподвижным.
Неподвижный блок можно рассматривать как рычаг, вращающийся вокруг точки, лежащей посередине рычага. Плечи такого рычага равны друг другу: OA = OB. В соответствии с условием равновесия рычага приложенные к блоку силы тоже равны: \( P=F \) . Следовательно, неподвижный блок не даёт выигрыша в силе, но он позволяет поднимать груз, прикладывая силу, направленную не вверх, а вниз, что облегчает перемещение груза.
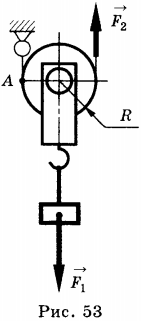
Чтобы получить выигрыш в силе используют подвижный блок (рис. 53). К нему непосредственно прикрепляется груз, один конец троса закрепляется, а к другому прикладывают силу и, таким образом, перебирая трос, поднимают блок с грузом.
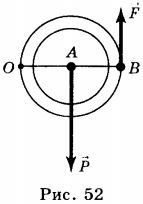
В этом случае точкой вращения блока является точка А (см. рис. 52).
Плечи действующих сил равны соответственно: AO и AB, при этом AB = 2AO. В соответствии с условием равновесия рычага: \( P=2F \) . Таким образом, подвижный блок даёт выигрыш в силе в 2 раза: \( F=P/2 \) .
Измерив расстояние \( h_1 \) , которое проходит груз, и расстояние \( h_2 \) , на которое перемещается конец троса, можно обнаружить, что расстояние \( h_2=2h_1 \) . Таким образом, подвижный блок даёт выигрыш в силе в 2 раза и в 2 раза проигрыш в пути. Соответственно, работа \( Ph_1=Fh_2 \) , т.е. \( A_1=2 \) . Подвижный блок, так же как и рычаг, не даёт выигрыша в работе.
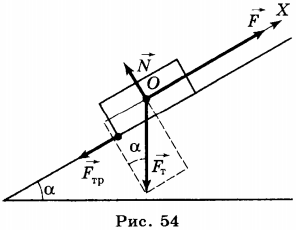
5. Наклонная плоскость используется в том случае, если нужно поднять объемный тяжёлый груз на какую-либо высоту (рис. 54).
Например, нужно погрузить ящик с металлическими деталями в кузов грузовика. В этом случае кладут массивную доску так, что она образует наклонную плоскость, один конец которой находится на земле, а другой на грузовике, и по этой плоскости втаскивают ящик. Чтобы поднять ящик вертикально вверх нужно приложить к нему силу, равную его весу \( P \) . Перемещая равномерно ящик по наклонной плоскости, в отсутствие трения прикладывают силу, равную \( F=P\sin\alpha \) , т.е. меньшую веса ящика, но при этом, выигрывая в силе, проигрывают в расстоянии. Работа по подъёму ящика по вертикали равна работе, совершаемой при его перемещении вдоль наклонной плоскости. Это справедливо, если сила сопротивления движению пренебрежимо мала. При наличии трения перемещение ящика вдоль наклонной плоскости требует совершения большей работы, чем при его движении вертикально вверх. В этом случае говорят о коэффициенте полезного действия (КПД) наклонной плоскости. Он равен отношению полезной работы ко всей совершённой работе: \( \mathbf<КПД>=A_п/A_с\cdot 100 \% \) , где \( A_п \) — полезная работа, \( A_п=mgh \) ; \( A_с \) — совершённая работа при перемещении ящика вдоль наклонной плоскости, \( A_c=Fl \) , где \( F \) — приложенная сила, \( l \) — длина наклонной плоскости.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Исследуя условия равновесия рычага, ученик выполнил соответствующую лабораторную работу. В таблице представлены значения сил и их плеч для рычага, находящегося в равновесии. Определите, чему равно плечо \( l_1 \) ?
1) 12,8 м
2) 2,5 м
3) 0,8 м
4) 0,25 м
2. Ученик выполнял лабораторную работу по исследованию условий равновесия рычага. Результаты для сил и их плеч, которые он получил, представлены в таблице.
Чему равна сила \( F_1 \) , если рычаг находится в равновесии?
1) 100 Н
2) 50 Н
3) 25 Н
4) 9 Н
1) 0,1 Н
2) 3,6 Н
3) 9 Н
4) 12 Н
4. Выигрыш в силе, приложенной к грузу, нельзя получить с помощью
1) подвижного блока
2) неподвижного блока
3) рычага
4) наклонной плоскости
5. С помощью неподвижного блока в отсутствие трения силе
1) выигрывают в 2 раза
2) не выигрывают, но и не проигрывают
3) проигрывают в 2 раза
4) возможен и выигрыш, и проигрыш
6. С помощью подвижного блока в отсутствие трения
1) выигрывают в работе в 2 раза
2) проигрывают в силе в 2 раза
3) не выигрывают в силе
4) выигрывают в силе в 2 раза
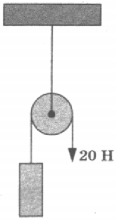
7. На рисунке изображён неподвижный блок, с помощью которого, прикладывая к свободному концу нити силу 20 Н, равномерно поднимают груз. Если трением пренебречь, то масса поднимаемого груза равна
1) 4 кг
2) 2 кг
3) 0,5 кг
4) 1 кг
8. Наклонная плоскость даёт выигрыш в силе в 2 раза. В работе при отсутствии силы трения эта плоскость
1) даёт выигрыш в 2 раза
2) даёт выигрыш в 4 раза
3) не даёт ни выигрыша, ни проигрыша
4) даёт проигрыш в 2 раза
9. Вдоль наклонной плоскости длиной 5 м поднимают груз массой 40 кг, прикладывая силу 160 Н. Чему равна высота наклонной плоскости, если трение при движении груза пренебрежимо мало?
1) 1,25 м
2) 2 м
3) 12,5 м
4) 20 м
10. Груз массой 10 кг поднимают по наклонной плоскости длиной 2 м и высотой 0,5 м, прикладывая силу 40 Н. Чему равен КПД наклонной плоскости?
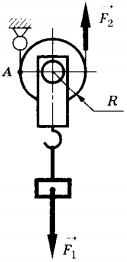
11. Груз поднимают с помощью подвижного блока радиусом \( R \) (см. рисунок). Установите соответствие между физическими величинами (левый столбец) и формулами, по которым они определяются (правый столбец).
Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) плечо силы \( \vec
Б) плечо силы \( \vec
B) момент силы \( \vec
ФОРМУЛЫ
1) \( F_1R \)
2) \( 2F_1R \)
3) \( \frac
4) \( R \)
5) \( 2R \)
12. Из перечня приведённых ниже высказываний выберите два правильных и запишите их номера в таблицу.
1) Любой простой механизм даёт выигрыш в силе.
2) Ни один простой механизм не даёт выигрыша в работе.
3) Наклонная плоскость выигрыша в силе не даёт.
4) Коэффициент полезного действия показывает, какая часть совершенной работы является полезной.
5) Неподвижный блок даёт выигрыш в силе в 2 раза.
Часть 2
13. Чему равна сила, с которой действуют на брусок массой 0,2 кг, перемещая его по наклонной плоскости длиной 1,6 м и высотой 0,4 м, если КПД наклонной плоскости 80%.