что дает эффективная граница портфеля
Портфель: золотая середина между риском и доходностью
Почему портфель лучше ставки на один актив?
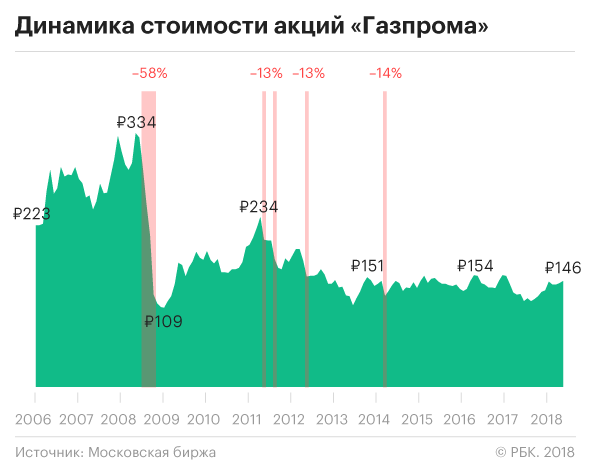
Чудес не бывает: чем более высокую доходность показывает актив в настоящий момент, тем выше риски, что заработок обернется убытками. Такие сверхизменчивые в цене инструменты как биткойн способны создавать и уничтожать целые состояния на очень коротком промежутке времени. Но и в истории «Газпрома» можно увидеть достаточно периодов, когда котировки стремительно падали, принося убытки инвесторам.
Поиск инвестиционной идеи усложняется, если учитывать при этом возможные убытки от вложений. Недостаточно просто найти актив, который может «выстрелить» — важно при этом оценить вероятность того, что «выстрел» будет направлен именно вверх. В идеале задача инвестора — получить приемлемую (например, вдвое выше банковского вклада) доходность при минимально возможных рисках.
Расчет рискованности конкретного инструмента — задача сложная. На первом этапе проще всего определять риск по следующей шкале:
Самый понятный способ контроля за рисками — распределить деньги между несколькими группами активов, иначе говоря — сформировать портфель. Еще в 1952 году Гарри Марковиц, аспирант Чикагского университета, доказал, что даже рискованные акции можно скомпоновать таким образом, что общий риск портфеля будет ниже риска входящих в него акций — за что и получил в 1990 году Нобелевскую премию.
Поставим эксперимент на примере российского рынка. В его истории был достаточно короткий период, за который он пережил поочередно катастрофическое падение (январь—декабрь 2008) и волшебное, пусть и чуть более длительное, восстановление (январь 2009-апрель 2011). Возьмем для примера 13 акций («Уралкалий», ВТБ, «Сургутнефтегаз», «Северсталь», «Сбербанк», «Ростелеком», МТС, ОГК-5 (ныне «Энел»), ЛУКОЙЛ, «Норникель», «Аэрофлот», «АвтоВАЗ», «Газпром») и сравним их поведение с динамикой трех индексов — ММВБ, ММВБ-10 и РТС (индексы по сути являются портфелями, т.к. при их расчете учитываются котировки сразу многих акций).
Ставка на одну акцию
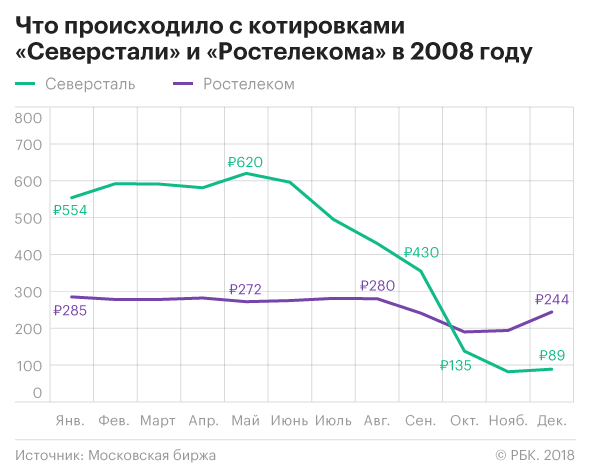
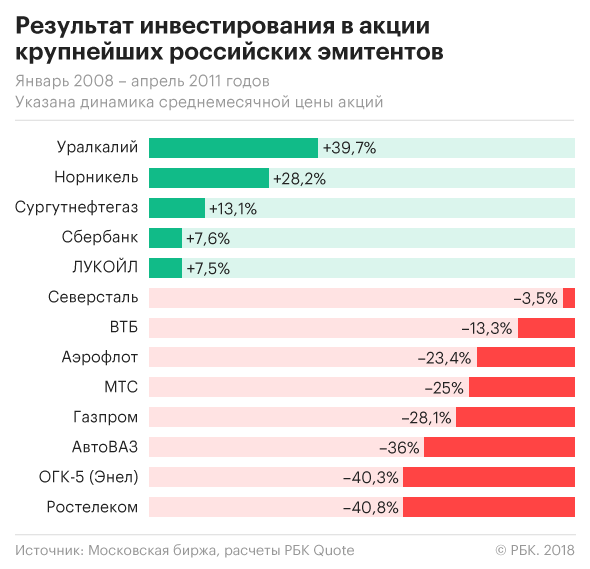
Если бы игрок хотел купить только одну акцию из всех 13 для инвестирования в 2008 году, выбором суперинвестора должны были быть акции «Ростелекома», они в том ужасном году потеряли лишь 15% своей стоимости.
Но предугадать такой исход в конце 2007 мог только гениальный игрок. В 2008 почти половину стоимости потерял ЛУКОЙЛ, около 4/5 — «Сбербанк», на 75% подешевели «АвтоВАЗ» и «Северсталь».
Игра на одной акции сродни рулетке. Кроме счастливого случая, объяснений таким удачам не существует. Если взять весь период и считать, что в указанные промежутки времени инвестор владел бы одной и той же акцией, то в восьми случаях из 13 он так и не смог бы вернуть инвестированных в начале денег.
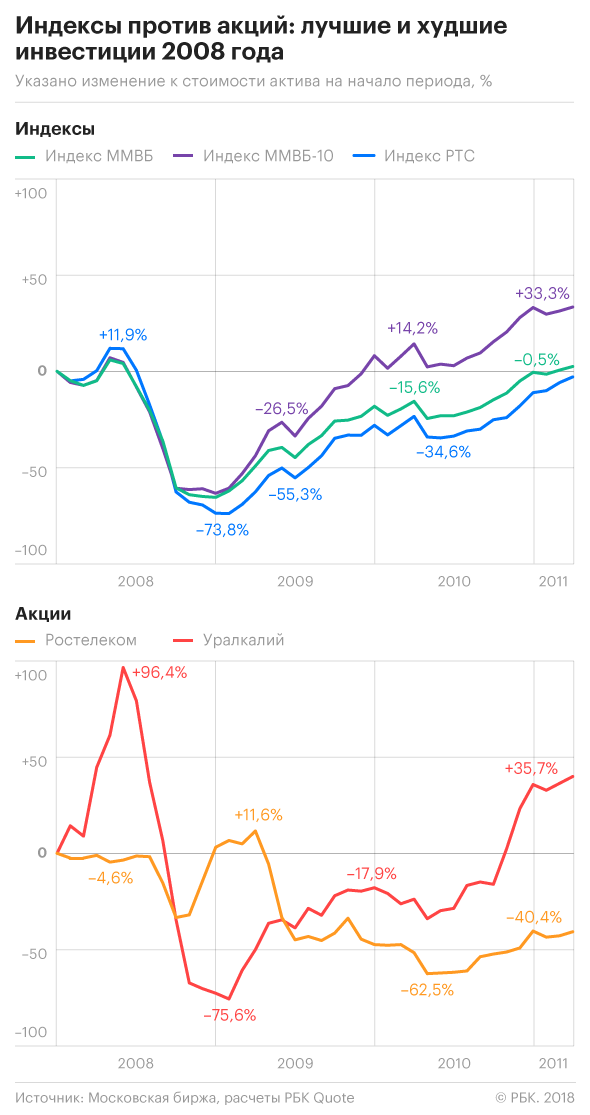
Как повели себя индексы
Как составить портфель самостоятельно?
Самый хороший вариант для старта: собрать портфель с минимальным риском. Для этого нужно разделить деньги между покупкой акций « голубых фишек » и гособлигаций. Какова пропорция? Тут можно применить простое эмпирическое правило, которое учитывает растущее стремление избегать рисков с течением времени: доля облигаций в портфеле должна соответствовать возрасту инвестора.
Высоконадежные и самые ликвидные акции на рынке со стабильными показателями доходности. Компании — «голубые фишки» — это лидеры в своей индустрии. Как правило, изменение цен на акции «голубых фишек» определяет настроение рынка. Лицо, выпускающее ценные бумаги. Эмитентом может быть как физическое лицо, так и юридическое (компании, органы исполнительной власти или местного самоуправления). Финансовый инстурмент, используемый для привлечения капитала. Основные типы ценных бумаг: акции (предоставляет владельцу право собственности), облигации (долговая ценная бумага) и их производные. Подробнее
Граница эффективности Марковица: обзор понятия
Портфельная теория Марковица лежит в основе современного метода инвестирования. А базовым камнем этой теории является граница эффективности, которая нередко вызывает трудности в понимании, что влечет искаженные представления об инвестиционном процессе. Ниже я попробую рассказать о границе эффективности по возможности простым языком.
Простейший случай
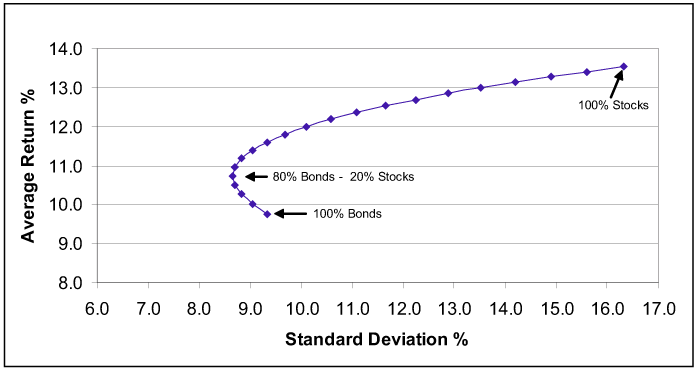
Самый простой случай, которым часто иллюстрируют эффективную границу — это портфель из американских акций и облигаций. Американский рынок имеет наиболее прослеживаемую историю: надежные данные по нему можно получить с 1926 года. Вот так выглядит картина границы эффективности на рынке США с 1926 по 2013 годы:
По оси Y у нас среднегодовая доходность, по оси Х — стандартное отклонение (колебания относительно средней доходности актива). В этом случае эффективная граница описывает все существующее множество портфелей. Как именно?
Нижняя точка — это среднесрочные пятилетние облигации. Иначе говоря, их держатель в периоде с 1926 по 2013 годы получил бы в среднем почти 10% годовых. Очень хорошая на сегодня доходность, сравнимая со средней доходностью акций — но стоит учитывать, что в 40-е и 70-е годы в США наблюдалась высокая инфляция и в эти периоды держателям облигаций не удавалось сохранить даже номинальную стоимость денег.
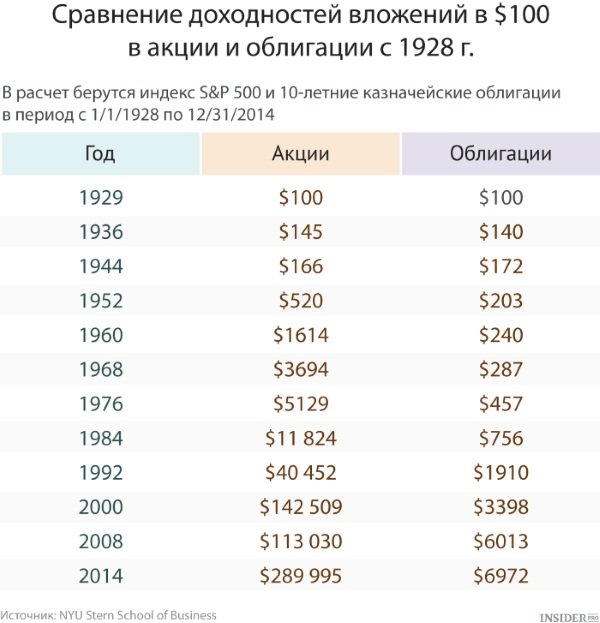
Верхняя правая точка означает доходность держателей акций американского рынка. Она ожидаемо выше — около 13.5% годовых, но и достигнута с заметно большим риском. Это значит, что держатели акций испытывали сильные просадки — несомненно, самая сильная была в Великую Депрессию, когда падение рынка США за 1929-1932 годы составило 90%. Вряд ли тогда кто-то верил в будущие перспективы американской экономики — но наш гипотетический держатель был вознагражден за риск. Кажется, что преимущество в 3.5% годовых не такое уж большое — но на дистанции разрыв в доходности получается громадным:
Наиболее интересным выглядит случай портфеля из 80% облигаций и 20% акций. Как мы видим из графика, такая комбинация обеспечила бы инвестору больший доход, чем в случае облигаций, и одновременно снизила бы общие колебания портфеля.
Т.е. в плане риска такой портфель был бы менее рискованным, чем 100% консервативных облигаций! И при этом более доходным!
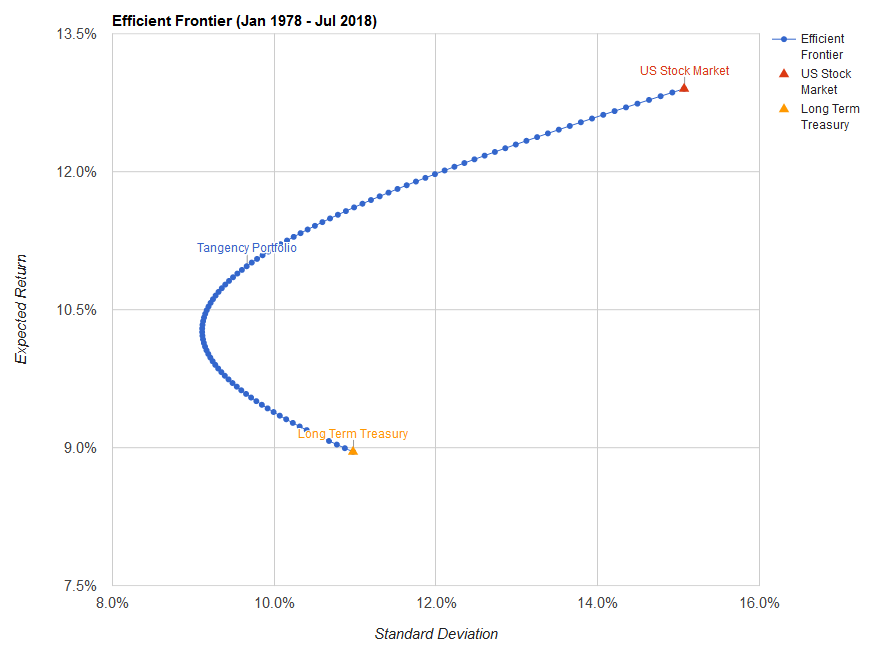
Выводом отсюда можно считать добавление небольшой доли акций в портфель даже тех инвесторов, которые консервативно относятся к своей доходности, предпочитая минимизировать просадки. Теперь рассмотрим тот же самый портфель с 1978 года:
Как видим, общая структура сохраняется. Высокая доходность облигаций здесь достигнута за счет очень высоких процентных ставок в конце 70-х — начале 80-х годов. Доходность акций также близка к предыдущему случаю и составляет около 12.5% годовых. Однако точка перегиба с минимальным стандартным отклонением будет иметь немного другой состав: около 35% акций и 65% облигаций.
Интересно, что при этом точка перегиба имеет практически тот же состав: 35% акций и 65% облигаций. Откуда можно сделать вывод, что при долгосрочных инвестициях соотношение около 70% облигаций и 30% акций может подойти консервативному инвестору.
Случай трех компонентов
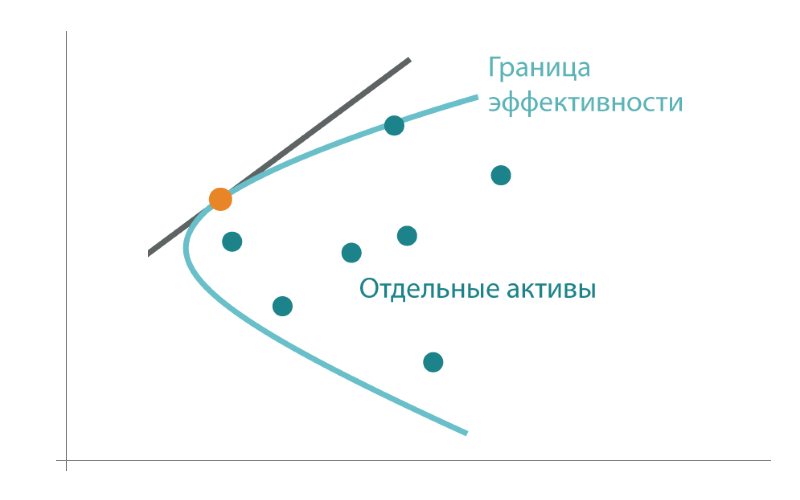
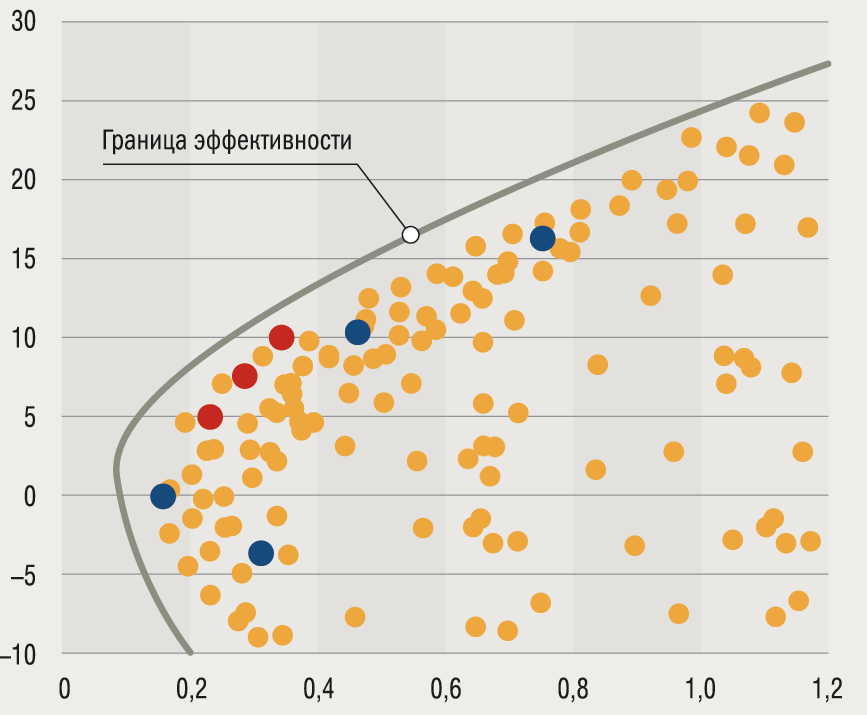
Однако ситуация резко меняется с добавлением третьего компонента, поскольку стремительно расширяется число возможных вариантов: из плоскости мы переходим в трехмерное измерение. В выбранных координатах доходность-риск они уже не будут помещаться на кривой эффективности (= границе эффективности), а займут некоторую область внутри этой границы, которую графически можно указать так:
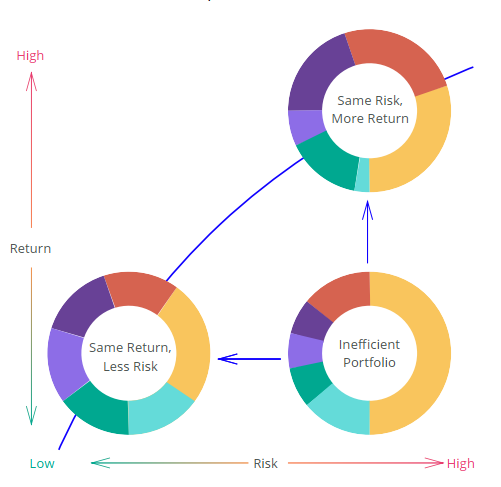
Чем правее и ниже от границы эффективности будут наши точки (портфели), тем больше риска придется брать инвестору и тем более низкую доходность он получит. Соответственно, взяв произвольную точку из глубины, мы получаем две возможности увеличить эффективность портфеля. А именно — двигаясь влево вдоль оси х мы не меняем доходность, но уменьшаем риск. А двигаясь вертикально вверх мы сохраняем уровень риска, но увеличиваем доходность:
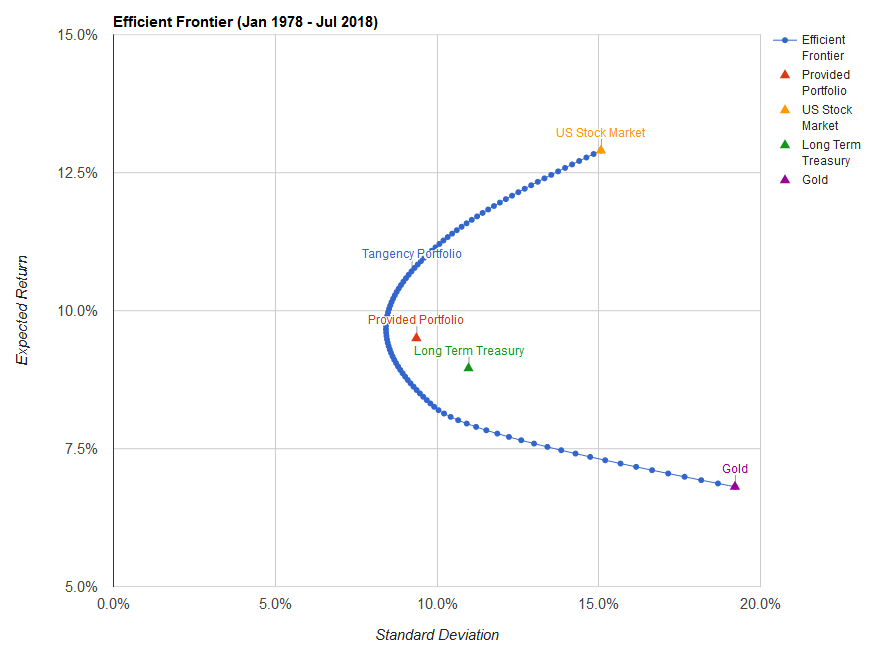
При этом варианты, лежащие на кривой эффективности, необязательно должны содержать портфель из всех трех компонентов — там вполне могут быть только два. Рассмотрим пример трехкомпонентного портфеля из американских акций, долгосрочных облигаций и золота:
Здесь нижняя часть границы эффективности представлена в виде прямой линии и состоит только из двух компонентов: золота и долгосрочных облигаций. Акции появляются выше и в точке перегиба портфель с минимальным риском состоит из 45% облигаций, 50% акций и 5% золота.
Такую точку можно представить в трехмерном пространстве как вершину горы — движение оттуда в любом направлении ведет вниз, т.е. увеличит риски портфеля. В другой формулировке повышение доходности портфеля из этой точки возможно лишь при принятии большего риска. Выбранный мной портфель (Provided Portfolio) с равными долями всех компонентов оказывается недалек от эффективной границы — он имеет примерно равную с точкой перегиба доходность в 9.5% годовых и является чуть более рискованным.
Верхняя часть кривой не содержит золота. Интересно, что в данном случае заметно более доходный актив в виде американских акций оказывается менее рискованным, чем самый низкодоходный — золото. Т.е. имея возможность инвестировать в американские акции, облигации и золото в любом соотношении худшим вариантом был бы вложить все деньги в золото. Но даже в этом случае доходность составила бы 6.8% годовых. Инфляция в США с 1978 по 2018 год составила около 3.5% в год.
Портфель из четырех компонентов
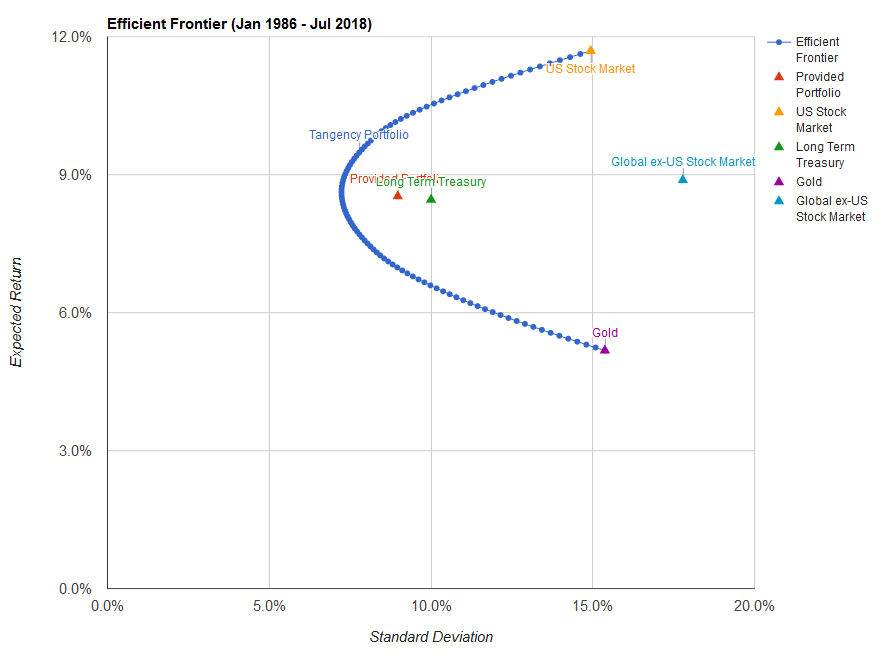
Картина принципиально не изменится, если мы добавим в рассмотрение четвертый компонент — акции других стран, кроме США:
Здесь портфель в точке перегиба содержит только три компонента: 40% американских акций, 53% облигаций и 7% золота. Портфель с равными долями вновь оказывается недалек от эффективной границы. Интересно, что глобальные акции оказались по доходности лишь чуть выше долгосрочных американских облигаций — но одновременно были самым рискованным компонентом. При этом можно заметить, что эффективная граница немного больше выгнута влево, чем в предыдущих случаях — увеличение числа компонентов повышает число комбинаций, снижающих риск портфеля.
Выводы
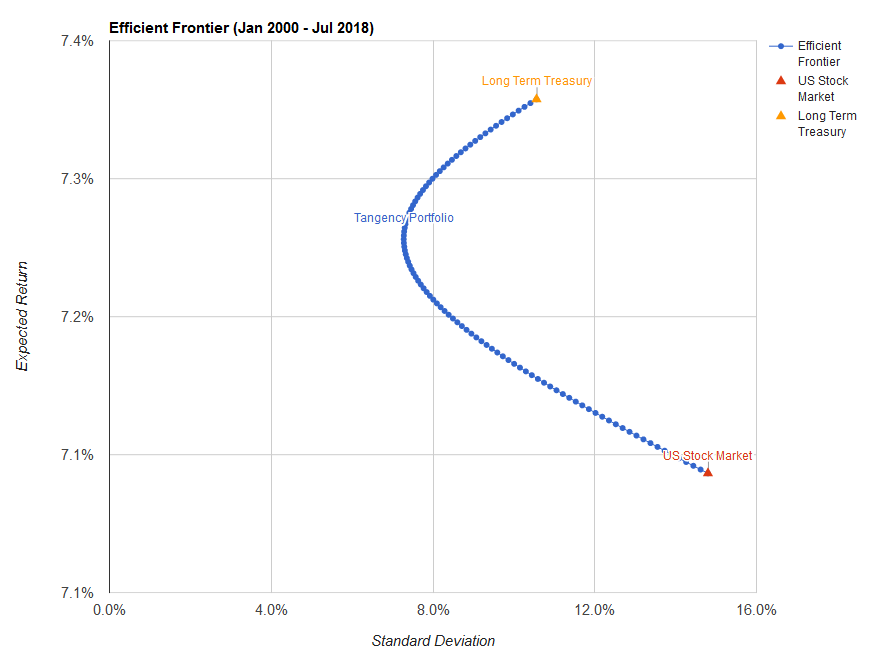
Можно лишь предполагать, какой актив окажется на вашем горизонте инвестирования самым доходным. На длинных участках это как правило акции — но между тем вариант 2000-2018 года показывает, что это не всегда так. К тому же акции можно разбить на американские, развитых и развивающихся рынков. Кто придет первым?
Золото, оказывавшееся внизу диаграмм, на промежутке с 2000 по 2010 годы заметно обогнало американский рынок. В общем случае для одного класса активов (скажем, акций США) у нас есть две неизвестных: будущая доходность на нужном нам промежутке времени, и риск, с которым эта доходность будет достигнута. В случае двух компонентов сюда добавляется их взаимное поведение (корреляция). Т.е. уже в случае двух точек (например, акций и облигаций) мы имеем пять неизвестных. И т.д.
Поэтому у инвестора нет задачи составить самый эффективный портфель. Да и эффективность понятие относительное — для кого-то она в минимизации риска, для кого-то в максимизации доходности. Но рассмотрев совокупность вариантов инвестор может избежать тех из них, которые исторически наиболее часто показывали наихудшую доходность и высокий риск.
Составление инвестиционного портфеля по Марковицу для чайников
В данном обзоре мы представим простой пример составления оптимального инвестиционного портфеля по Марковицу.
Введение в портфельную теорию
Портфельная теория Марковица была обнародована в 1952 году. Позже автор получил за нее Нобелевскую премию.
Целью модели является составление оптимального портфеля, то есть с минимальным риском и максимальной доходностью.
Как правило, решается две задачи: максимизация доходности при заданном уровне риска и минимизация риска при минимально допустимом значении доходности.
Доходность портфеля измеряется как средневзвешенная сумма доходностей входящих в него бумаг.
wi — доля инструмента в портфеле;
ri — доходность инструмента.
Риск отдельного инструмента оценивается как среднеквадратичное (стандартное) отклонение его доходности. Для расчета общего риска портфеля необходимо отразить совокупное изменение рисков отдельного инструмента и их взаимное влияние (через ковариации и корреляции — меры взаимосвязи).
σi — стандартное отклонение доходностей инструмента;
kij — коэффициент корреляции между I,j-м инструментом;
Vij — ковариация доходностей i-го и j-го финансового инструмента;
n — количество финансовых инструментов в рамках портфеля.
Таким образом, в рамках правильно подобранного портфеля риски снижаются за счет обратной корреляции инструментов. При этом устраняются не только специфические риски инструмента, но и снижается систематический (рыночный) риск.
Для составления портфеля решается оптимизационная задача. При этом в базовом виде использование заемных средств не предполагается, то есть сумма долей активов равняется единице, а доли эти положительны.
Минимизируем риск при минимально допустимом уровне доходности
Максимизируем доходность при заданном уровне риска
Пример расчетов в Excel
Оптимальный портфель содержит различные группы активов — акции, облигации, товарные фьючерсы и т.д. Так легче подобрать инструменты с отрицательной корреляцией и минимизировать риски.
В нашем примере будет использован более простой подход — составление портфеля из нескольких американских акций. Для эффекта диверсификации возьмем представителей различных секторов — платежную систему VISA, ритейлера Macy’s, технологичного гиганта Apple и телеком AT&T.
Сразу отмечу, что это лишь пример. Все эмитенты интересны, но для грамотного составления портфеля необходимо учитывать фундаментальные показатели, включая рыночные мультипликаторы, оценивать технические уровни для входа в позицию.
Этап 1. Выкачиваем котировки. Необходимо взять данные минимум за год. В нашем примере были взяты ежемесячные цены закрытия с 31.06.2017 по 31.05.2018.
Этап 2. Считаем доходности по каждой бумаге. Для простоты не будем учитывать эффект дивидендов.
Считаем доходность за каждый месяц по формуле натурального логарифма. К примеру, доходность VISA за май 2018 = LN(C14/C13)
Для расчета ожидаемой доходности берем среднее значение за рассматриваемый период. В нашем случае это год. Ожидаемая доходность VISA = СРЗНАЧ(G3:G14)
Получаем отрицательную доходность AT&T, и убираем бумагу из портфеля. Сразу отмечу, что в этом заключается недостаток модели, ведь просевшие ранее акции в перспективе могут развернуться.
Этап 3. Расчет риска каждой акции. Производится по формуле стандартного отклонения. К примеру, риск VISA =СТАНДОТКЛОН(G3:G14)
Указываем окне входной интервал — ежемесячные доходности акций, а в опции «Группирование» выбираем «по столбцам».
В результате получаем ковариационную матрицу.
Этап 5. Расчет общей доходности портфеля. Для начала установим произвольные доли бумаг в портфеле. Они положительны, их сумма равна 1.
Считаем средневзвешенное значение доходностей отдельных акций. Воспользуемся формулой G15*G23+H15*H23+I15*I23
Этап 6. Расчет общего риска портфеля. Производится по формуле массива КОРЕНЬ(МУМНОЖ(МУМНОЖ(G23:I23;G20:I22); E20:E22))
Этап 7. Портфель минимального риска.
Речь идет о долях отдельных бумаг в портфеле. Для начала необходимо определить минимальный уровень допустимой доходности портфеля (rp). Возьмем rp >= 3,2%.
При оценке долей акций воспользуемся надстройкой в Excel «Поиск решений», для этого выбираем Главное меню → «Данные» → «Поиск решений».
В надстройке «Поиск решений» необходимо ввести ссылку на ячейку, которую следует оптимизировать (общий риск портфеля, минимизируем), ввести какие параметры необходимо изменять (доли акций) и ограничения. Введем ограничения на весовые значения коэффициентов у акций: сумма долей акций должна быть равна 1 и сами доли должны иметь положительный знак.
В результате имеем портфель с 73% долей VISA и 27% долей Macy’s.
Визуально портфель выглядит так:
Этап 8. Портфель максимальной доходности.
Для начала необходимо определить максимальный уровень допустимого риска портфеля (σp). Возьмем σp 30
Последние новости
Рекомендованные новости
Главное за неделю. Паника в понедельник и пятницу
Итоги торгов. Упасть в пятницу — это уже традиция
Рынки снова падают из-за коронавируса. Что делать
Alibaba: время присмотреться к покупкам
Как следить за американскими дивидендами: удобный календарь
Новый штамм коронавируса из Южной Африки. Что нам известно
В каких акциях можно пересидеть новые локдауны
В декабре структура индексов Мосбиржи поменяется. Кто на новенького
Адрес для вопросов и предложений по сайту: bcs-express@bcs.ru
* Материалы, представленные в данном разделе, не являются индивидуальными инвестиционными рекомендациями. Финансовые инструменты либо операции, упомянутые в данном разделе, могут не подходить Вам, не соответствовать Вашему инвестиционному профилю, финансовому положению, опыту инвестиций, знаниям, инвестиционным целям, отношению к риску и доходности. Определение соответствия финансового инструмента либо операции инвестиционным целям, инвестиционному горизонту и толерантности к риску является задачей инвестора. ООО «Компания БКС» не несет ответственности за возможные убытки инвестора в случае совершения операций, либо инвестирования в финансовые инструменты, упомянутые в данном разделе.
Информация не может рассматриваться как публичная оферта, предложение или приглашение приобрести, или продать какие-либо ценные бумаги, иные финансовые инструменты, совершить с ними сделки. Информация не может рассматриваться в качестве гарантий или обещаний в будущем доходности вложений, уровня риска, размера издержек, безубыточности инвестиций. Результат инвестирования в прошлом не определяет дохода в будущем. Не является рекламой ценных бумаг. Перед принятием инвестиционного решения Инвестору необходимо самостоятельно оценить экономические риски и выгоды, налоговые, юридические, бухгалтерские последствия заключения сделки, свою готовность и возможность принять такие риски. Клиент также несет расходы на оплату брокерских и депозитарных услуг, подачи поручений по телефону, иные расходы, подлежащие оплате клиентом. Полный список тарифов ООО «Компания БКС» приведен в приложении № 11 к Регламенту оказания услуг на рынке ценных бумаг ООО «Компания БКС». Перед совершением сделок вам также необходимо ознакомиться с: уведомлением о рисках, связанных с осуществлением операций на рынке ценных бумаг; информацией о рисках клиента, связанных с совершением сделок с неполным покрытием, возникновением непокрытых позиций, временно непокрытых позиций; заявлением, раскрывающим риски, связанные с проведением операций на рынке фьючерсных контрактов, форвардных контрактов и опционов; декларацией о рисках, связанных с приобретением иностранных ценных бумаг.
Приведенная информация и мнения составлены на основе публичных источников, которые признаны надежными, однако за достоверность предоставленной информации ООО «Компания БКС» ответственности не несёт. Приведенная информация и мнения формируются различными экспертами, в том числе независимыми, и мнение по одной и той же ситуации может кардинально различаться даже среди экспертов БКС. Принимая во внимание вышесказанное, не следует полагаться исключительно на представленные материалы в ущерб проведению независимого анализа. ООО «Компания БКС» и её аффилированные лица и сотрудники не несут ответственности за использование данной информации, за прямой или косвенный ущерб, наступивший вследствие использования данной информации, а также за ее достоверность.
Что произойдет в долгосрочной перспективе, если добавить 10% акций в портфель из облигаций?
Что произойдет в долгосрочном периоде, если добавить в портфель из облигаций 10% акций? Варианты:
Будущее поведение активов непредсказуемо, и многое зависит от того, о каких именно облигациях и акциях идет речь. Но исторические данные показывают, что весьма вероятен третий вариант: если добавить 10% акций в облигационный портфель, доходность будет выше, а риск — ниже.
Такой результат достигается благодаря портфельному эффекту: сочетание активов со слабой корреляцией делает портфель эффективнее. Я объясню, как это работает, и для наглядности разберу несколько примеров.
Как победить выгорание
Эффективная граница портфелей
Принципы построения оптимального портфеля путем распределения долей различных классов активов описывает современная теория портфеля, которую предложил Гарри Марковиц в 1952 году.
Теория подразумевает, что мы ищем идеальную смесь инструментов, которые позволят максимизировать доходность портфеля при заданном уровне риска. При этом все множество оптимальных портфелей образует так называемую эффективную границу.
Рассмотрим, как это работает, опираясь на исследование A Retirement Portfolio’s Efficient Frontier, опубликованное в 2015 году. В нем были проанализированы исторические данные по акциям и облигациям с 1950 по 2012 год.
A Retirement Portfolio’s Efficient FrontierPDF, 395 КБ
Результаты акций и облигаций с 1950 по 2012 год
| Акции | Облигации | |
|---|---|---|
| Среднеарифметическая доходность | 12,44% | 6,71% |
| Среднегеометрическая доходность | 11,00% | 6,21% |
| Стандартное отклонение | 17,52% | 10,84% |
Коэффициент корреляции между двумя инструментами за этот период составил 0,11, то есть их поведение заметно отличалось. Используя данные о доходности, стандартном отклонении доходности — мере риска — и коэффициенте корреляции, исследователи построили множество портфелей с различными комбинациями акций и облигаций.
Посмотрим на результаты разных портфелей, если менять доли инструментов в них с шагом 25%.
Показатели портфелей с изменением долей инструментов в них на 25%
| Доля акций | Доля облигаций | Стандартное отклонение | Доходность |
|---|---|---|---|
| 100% | 0% | 17,5% | 11,0% |
| 75% | 25% | 13,7% | 9,8% |
| 50% | 50% | 10,8% | 8,6% |
| 25% | 75% | 9,6% | 7,4% |
| 0% | 100% | 10,8% | 6,2% |
Второе, что бросается в глаза: портфель, который на 100% состоит из облигаций, имеет такой же уровень риска, как и портфель из акций и облигаций в соотношении 50/50. Стандартное отклонение у обоих составляет 10,8%, но годовая доходность второго портфеля при этом на 2,4 п. п. больше. Соответственно, его коэффициент Шарпа выше.
Как считается коэффициент Шарпа и стандартное отклонение, я писал в статье про всепогодную стратегию.
Ниже показана эффективная граница — портфели, которые дают максимальный возможный доход на заданный уровень риска или, наоборот, у которых минимальный риск при заданной доходности.
А вот еще несколько эффективных границ из другого источника за гораздо более длинный период — с 1802 по 2012 год. Здесь видно, что граница эффективности также зависит от горизонта инвестирования:
Тестирование портфелей на исторических данных
Чтобы было нагляднее, сравню облигационные портфели с портфелями, где 10% отведено на акции. Для этого пригодятся сервис Portfolio Visualizer и бэктестер на сайте Capital Gain.
Портфели американских активов. Первый портфель составим на 100% из долгосрочных облигаций казначейства США — фонд TLT. Во втором портфеле добавим к казначейским облигациям 10% акций согласно индексу S&P 500 — фонд SPY.
Результаты американских портфелей с августа 2002 по февраль 2021 года
Как видим, добавление 10% акций увеличило доходность второго портфеля на 0,65 п. п. в год. Это неудивительно: акции — исторически более доходный инструмент при долгосрочных вложениях.
Стандартное отклонение доходности у портфеля, в который добавили акции, на 1,6 п. п. ниже, чем у облигационного: 11,52 против 13,12%. Получается, что портфель с небольшой долей акций был менее рискованным, чем портфель без акций.
Об этом же говорит и значение максимальной просадки. По итогам 2009 года портфель с 10% акций упал на 3,95 п. п. меньше, чем портфель только из облигаций.
Коэффициент Шарпа, то есть соотношение доходности к риску, у портфеля с 10% акций выше, чем у облигационного портфеля. Иными словами, добавление небольшой доли акций в портфель делает его эффективнее.
Результаты мировых портфелей с 1988 по 2020 год
Тут ситуация немного другая. Включение акций позволило увеличить доходность портфеля, но при этом выросла волатильность. Правда, коэффициент Шарпа у портфеля с 10% акций все же чуть выше, то есть сочетание доходности и риска получилось более интересным.
Результаты российских портфелей с 2003 по 2020 год
| Портфель | Итог | Среднегодовая доходность | Стандартное отклонение | Худший год | Коэфф. Шарпа |
|---|---|---|---|---|---|
| 100% российские гособлигации | 62 091 Р | 10,68% | 11,97% | −21,8% | 0,23 |
| 90% облигации и 10% акции индекса Мосбиржи | 75 462 Р | 11,88% | 13,96% | −17,85% | 0,28 |
О чем стоит помнить
Активы могут вести себя по-разному на разных отрезках времени. Результат за год или несколько лет может сильно отличаться от усредненных исторических данных за длительные интервалы.
Например, с 2000 по 2009 годы американские инвесторы столкнулись с двумя серьезными кризисами. За эти 10 лет рынок акций США проиграл американскому рынку облигаций: акции дали −0,27% годовых, облигации — 6,06%. Добавление 10% акций США к американским облигациям снизило бы доходность портфеля, повысило его волатильность и усилило просадки его стоимости.
Получается, что многое зависит от выбранных активов и корреляции между ними. Может влиять даже частота ребалансировки портфеля. Весьма вероятно, что если добавить 10% акций в портфель облигаций, то его характеристики улучшатся, но гарантировать это нельзя: бывало и иначе.
Еще стоит учесть, что добавление акций в облигационный портфель может снизить его прогнозируемость. Если инвестор вкладывает деньги в отдельные облигации и держит их до погашения, он заранее знает, сколько заработает и каким примерно будет в итоге его капитал. С акциями так не получится, поскольку их доходность заранее неизвестна.
Что в итоге
Включение небольшой доли акций в портфель из облигаций может не только увеличить доходность, но и одновременно с этим снизить риск. Это позволяет создавать более эффективные портфели, в частности пенсионные, которые вряд ли стоит полностью держать в облигациях.
При составлении оптимального портфеля можно не только комбинировать акции с облигациями, но и добавлять альтернативные классы активов: золото, недвижимость и т. д. Чем ниже корреляция между инструментами, тем проще оптимизировать портфель.
Коэффициент Шарпа помогает оценить качество портфеля на исторических данных. Чем он выше, тем более эффективен портфель: его доходность на единицу риска выше.
Прошлые результаты не гарантируют, что они повторятся в будущем, — могут быть сюрпризы. Кроме того, усредненные данные за много лет не означают, что такой эффект будет на любых временных отрезках, особенно коротких. Однако подобные знания все же помогают инвестировать эффективнее.
Что делать? Читатели спрашивают — эксперты Т—Ж отвечают