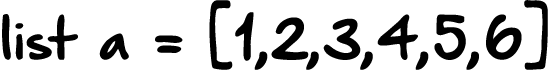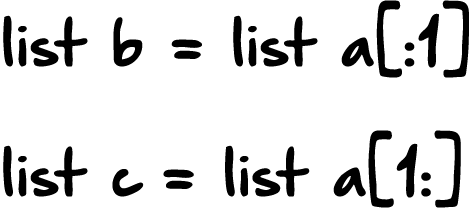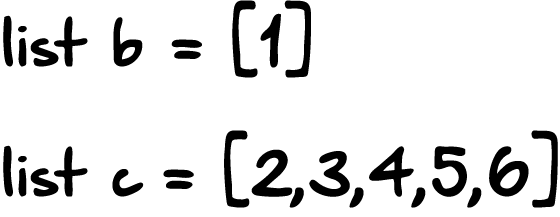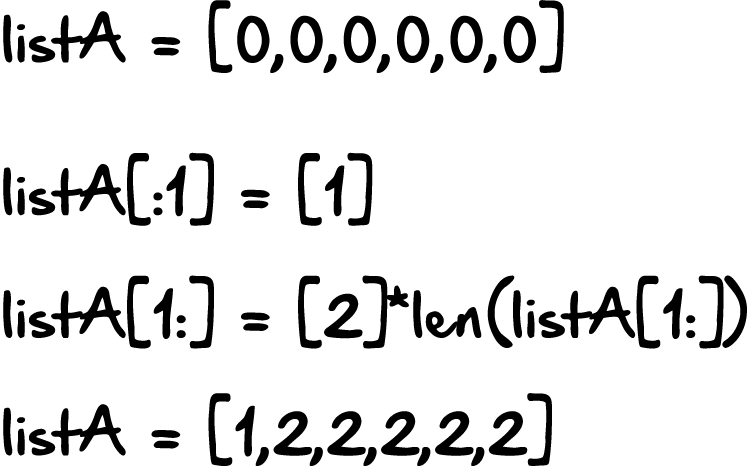чем рекурсия лучше цикла
Мощь алгоритмов: автоматический поиск всех возможных комбинаций
Сдвигаем парадигму с помощью силы компьютеров
Это история об информатике, алгоритмах и понимании мощи компьютеров.
Представим такую ситуацию: компания по продаже компьютеров хочет написать самую эффективную рассылку для своих клиентов. Маркетологи сказали, что в письме обязательно должно быть 4 блока:
Но никто не знал, в каком порядке лучше всего расположить эти блоки, чтобы рассылка сработала максимально круто. В итоге решили перебрать все комбинации и отправить много разных рассылок. Для этого позвали программиста, который написал для них простой скрипт — он выводит все варианты расположения блоков. Сегодня мы попробуем это повторить.
О чём речь
В математике это называется перестановками без повторений: мы просто перебираем все разные варианты, в каком порядке могут идти элементы. В нашем случае может быть так:
Таких вариантов можно составить 4! («четыре факториал») — то есть 24 штуки. Восклицательный знак означает факториал, то есть нам нужно перемножить все числа от 1 до этого числа:
Получается, из четырёх блоков можно сделать 24 разных варианта письма. Вручную перебирать их все сложно, да и нет смысла: компьютер с этим справится гораздо быстрее. Для этого и сделаем алгоритм.
В чём идея
Чтобы перебрать все варианты, можно сделать так:
Но это сложно: нам нужно заводить для каждого цикла свою переменную, а потом следить, чтобы они не перепутались между собой. А ещё нужно не забыть:
А можно подойти к вопросу иначе:
Обратите внимание, что у нас получился только один цикл, который перебирает по очереди все элементы массива. А вот внутри этого цикла и происходит вся магия: мы погружаемся всё глубже и глубже по одним и тем же правилам, а потом начинаем собирать результаты с конца.
На самом деле мы только что описали рекурсию: функцию, которая вызывает сама себя, но на каждом шаге с новыми условиями.
Почему рекурсия лучше вложенных циклов
Когда вложенных циклов мало, то с ними проще: можно контролировать всё вручную. А вот когда циклов становится не три, а 10 или 50, то сильно вырастает вероятность ошибиться в переменной или забыть про какое-то условие. В рекурсии такой проблемы нет: мы один раз описываем, как нырнуть и как оттуда вынырнуть, и всё, остальное компьютер сделает сам.
Ещё бывает такое, что мы заранее не знаем, сколько будет блоков для перестановок — 4 или 40, например. Рекурсия здесь тоже выигрывает: достаточно в одном цикле перебрать все элементы массива, а дальше всё сработает само.
Алгоритм
Единственное, что нам понадобится нового для рекурсии, о чём мы ещё не говорили, — это мемоизация.
В программировании мемоизацией называют временное хранение промежуточных результатов вычислений, чтобы не вычислять их по сто раз. Один раз посчитал, добавил в переменную-кеш — и отлично.
В нашем случае за это будет отвечать такая строчка:
Она появляется в самом начале рекурсии и означает вот что:
Так мы избавляемся от необходимости высчитывать промежуточные последовательности заново, а вместо этого используем временное хранилище.
Теперь смотрите код и читайте комментарии:
Запустим код в консоли браузера:
Видно, что мы получили 24 перестановки, как и должно было быть. Они все разные, ни в одной нет повторений — то, что нам нужно. Теперь можно отдать эти последовательности дальше, чтобы по каждой из них собрали своё письмо для клиентов.
Если интересно, как рекурсия справится со сложными вариантами и сколько их получится, — сделайте в исходном массиве в коде не 4, а 10 элементов.
Что дальше
Попробуем использовать этот же подход в задаче коммивояжёра — там тоже есть много вложенных циклов. Должно сработать.
Рекурсия и цикл, в чем разница? На примере Python
Apr 4, 2019 · 10 min read
Цикл — это фундаментальный инструмент в программировании. Существует множество различных типов циклов, но почти все они выполнят одну базовую функцию: повторение определённых действий над данными, для их анализа или управления ими. Рекурсия, так же распространённый способ анализировать и манипулировать данными, как и цикл, но как правило, менее понятный и часто более запутанный. Почти все рекурсивные функции можно переписать в циклы, и наоборот. Тем не менее, каждый тип функции имеет свои преимущества и недостатки, и сегодня вы узнаете, в каких случаях применять тот или иной метод. В статье мы разберём следующие вопросы:
Начнём с м етода, который кажется более простым из этих двух.
Циклы for
Цикл for используют для перебора последовательности данных (списка, кортежа, словаря, набора или строки). При достижении конца последовательности цикл завершается.
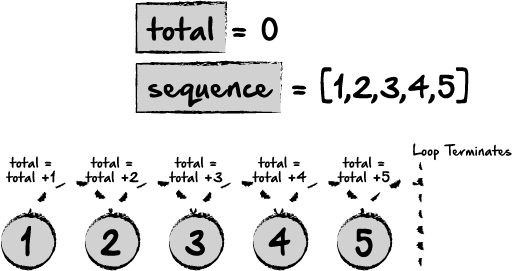
Например, вам нужно сложить числа от 1 до 5 и получить их сумму. Конечно, вы можете просто суммировать 1+2+3+4+5. Но, создать функцию намного удобнее, потому что вы сможете использовать её повторно, причём подставляя любые значения, даже если они не известны заранее.
Это будет выглядеть примерно так:
Для работы такого цикла, нам нужно хранить список всех чисел, чтобы мы могли перебирать элементы и складывать их в итоговое значение.
Вот как это выглядит в коде:
Запустив код, мы увидим, что все числа на своих местах и нам возвращается их сумма.
Рекурсия
Если функция вызывает сама себя, то это является признаком рекурсии. Одно из важнейших отличий рекурсии от цикла, это способ завершения рекурсивной функции. В приведённом выше примере цикл for завершается в конце последовательности, в которой он выполняется. А вот рекурсивная функция может продолжаться бесконечно, потому что она может не иметь последовательности данных. Вместо этого у рекурсивной функции есть так называемое базовое условие. Базовое условие определяет, когда цикл должен завершится.
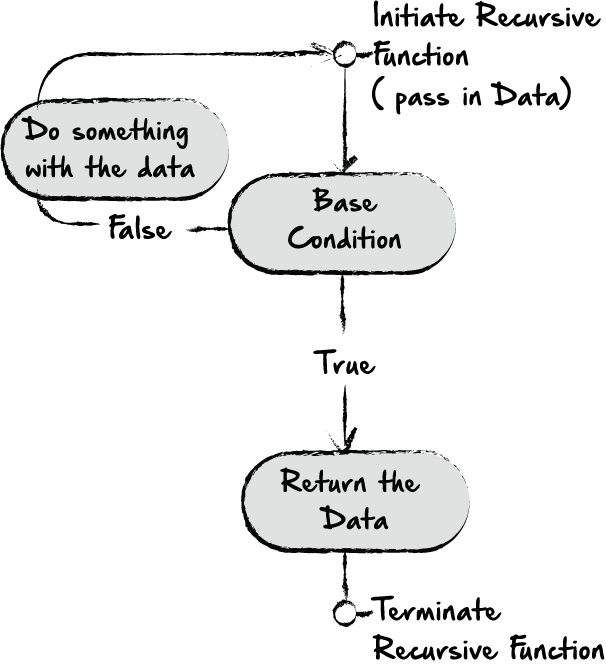
Давайте попробуем решить предыдущую задачу рекурсивным способом. Визуально это выглядит так:
Каждый раз функция либо вызывает себя с новыми входными данными, либо возвращает значение.
Вот как это выглядит в коде:
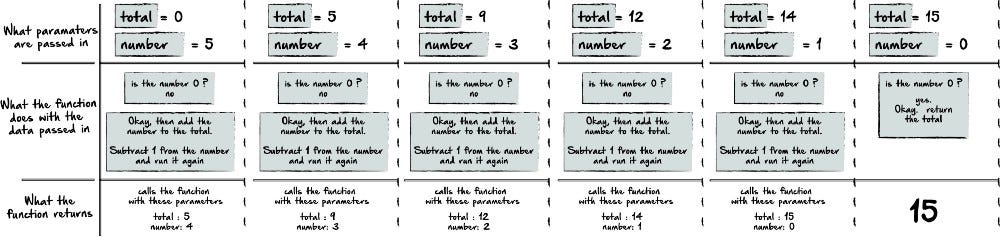
Как видите мы передаём два значения: начальное и итоговое. При первом вызове функции итоговое значение равно 0, а начальное 5. Мы проверяем, является ли начальное число 0. Если нет, то вызываем функцию снова, но на этот раз мы меняем входное значение на 5–1 и 0+5, и повторяем этот процесс до тех пор, пока n не будет равно 0. После выполнения этого условия мы возвращаем итоговое значение (15).
Вычисление сложного процента рекурсией и циклом FOR
Давайте разберём более сложную задачу. Нужно определить стоимость кредита или инвестиции со сложным процентом. Чтобы это сделать, нам нужны следующие данные:
Формула расчёта сложного процента:
Так мы можем рассчитать всю сумму сразу. Но вместо этого, для расчёта мы используем цикл или рекурсию. В таком случае переменная времени (nt) будет обрабатываться в итерациях.
Давайте сразу создадим переменные, в которых будем хранить исходные числа и используем их в обоих методах:
Расчёт по сложной процентной ставке итеративно
Давайте сразу посчитаем общее количество платежей, чтобы упростить вычисление в цикле. Так как платежи ежемесячные, а количество лет равно 10, то результат будет 120, или 10*12. Теперь мы можем вычислять процент для каждого месяца и добавлять результат каждой итерации к основной сумме.
Так выглядит код:
Единственное различие между этим и предыдущим примерами заключается в том, что мы делаем на несколько вычислений больше во время каждой итерации. Также увеличилось число итераций с 5 до 120.
Результат наших вычислений:
Расчёт по сложной процентной ставке рекурсивным способом
В предыдущем примере последовательность данных равна 120, что отражает количество раз, когда основная сумма пересчитывается. Цикл прерывается по завершении последовательности. Рекурсивный метод позволяет нам поступить схожим образом, т.е. инициализировать счётчик и задать два условия.
Выполнить вычисление сложного процента. Добавить результат вычисления к общей сумме. Уменьшить значение счётчика на 1. Повторить те же действия, подставив новое значения для счётчика и общей суммы.
В предыдущем примере, цикл функции начинался со значения 5 и завершался при 0.
Здесь происходит тоже самое, только начальное значение теперь 120
Здесь мы либо снова вызываем функцию, либо возвращаем обновлённую общую сумму. Каждый раз вызывая функцию, значение счётчика уменьшается на 1. Возврат общей суммы происходит, когда счётчик равен 0.
Когда использовать рекурсию
Выбор между рекурсивным и итеративным методом может в значительной степени зависеть от языка, который вы используете, или от задачи, которую вы намерены решить. Например, в JavaScript рекурсия может привести к ошибкам stack frame errors, когда предел стека уже достигнут, а базовое условие ещё не выполнено. В таком случае, итеративный подход будет работать лучше.
Рассмотренный выше случай является хорошим примером того, когда рекурсия работает намного лучше, чем цикл.
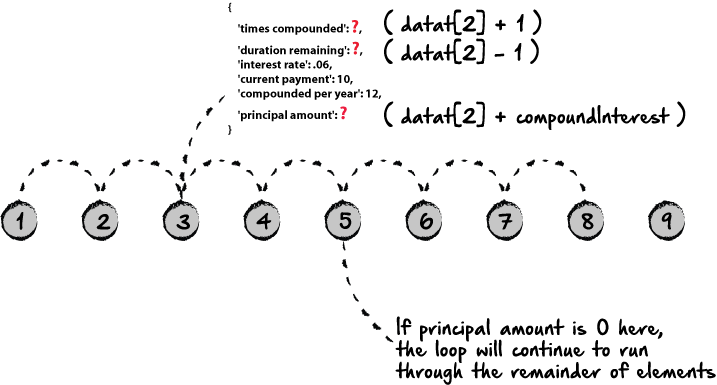
Давайте представим, что помимо тех чисел, которые мы использовали в предыдущем примере, нам нужно учитывать и другие данные. Например, мы можем отслеживать то, как регулярные платежи влияют на срок кредита. Возможно, мы захотим остановить цикл до завершения последовательности. Если общее количество раз, когда начисляются проценты по кредиту равно 120, то и длина списка равна 120. Но, если сумма кредита будет равна 0 уже после 100 итераций, то в конце списка останется 20 неиспользуемых и ненужных элементов списка. Проблема дальнейшего усложнения сценария цикла заключается в том, что значения переменных, таких как сумма кредита, зависит от значения той же переменной на предыдущей итерации. Дело не в том, что это сложно реализовать, а в том, что это грязно.
Визуализация данной проблемы:
Рекурсивные структуры данных
Именно в таких случаях рекурсивные структуры данных особенно полезны. Структуру можно назвать рекурсивной, если её можно определить в терминах меньшей версии самой себя. Список является примером рекурсивной структуры данных.
Например, возьмём такой список:
Теперь, сделаем на его основе два меньших списка:
Если вывести оба списка, то мы увидим следующее:
Благодаря рекурсивным функциям и рекурсивными структурам данных мы можем изменить весь список или меньшую часть большего списка за раз. Итеративный подход решения подобной проблемы, позволяет изменить только одно значение в одном индексе за раз.
Пример того, как это сделать:
Сохранив маленькие части большого списка, мы можем вызвать ту же функцию (рекурсия) и отправить ей эти части (рекурсивная структура данных).
Вот как это работает на примере с вычислением сложного процента:
Наша функция в основном состоит из операторов if и else. Мы можем усложнить эту структуру если понадобится, но она и в таком виде делает всё что нам нужно. В итоге, мы хотим вернуть окончательные данные, которые покажут нам сумму кредита и размер текущего платежа на каждой итерации, когда начисляется процент.
Визуализация процессов рекурсивной функции:
При каждом рекурсивном вызове мы будем брать первый элемент массива из списка. Затем мы изменим значения этого элемента и снова вызовем функцию, но на этот раз передадим ей в качестве параметров array[:1] и array[1:]. На картинке видно, что, достигнув середины списка, мы будем иметь две его части одинакового размера. А уже к концу мы полностью переберём и модифицируем все элементы первого списка, и добавим их во второй список. Далее мы шаг за шагом реализуем эту функцию в коде.
Шаг 1: создаём массив
На данном этапе, наш массив имеет длину равную числу раз, когда начисляется процент. Каждый элемент содержит одинаковые данные, которые мы будем изменять рекурсивно.
Шаг 2: создаём функцию и базовое условие
Базовое условие будет учитывать два возможных сценария. Либо счётчик достигнул конца последовательности ( len(inputArr) == 0 ), либо мы погасили кредит раньше ( inputArr[-1][‘principal amount’] ).
Шаг 3: создаём выражение else и определяем переменные current, inputArray и outputArray
Шаг 4: если массив outputArray пуст, то берём первый элемент из массива входных данных и помещаем его в массив выходных данных без изменений.
Теперь оба массива выглядят как на картинке, которую вы видели выше, в момент первого вызова рекурсивной функции.
Шаг 5: если массив выходных данных не пуст, то изменяем все значения текущего элемента.
Шаг 6: добавляем переменную newCurrent к массиву outputArray
Шаг 7: вызываем рекурсивную функцию с новыми параметрами
Мы закончили! Так выглядит код целиком:
Чтобы убедиться, что код работает так, как мы задумали, давайте увеличим сумму платежа.
Если изменить сумму платежа на 2000, то при выводе должны получиться такие данные:
Такой код возвращает более чистый результат, чем при использовании цикла. Если бы мы использовали итеративный подход, то нам пришлось бы перебрать все 120 элементов, большинство из которых были бы бесполезны/пусты.
Заключение
На первый взгляд рекурсия может показаться сложной. Но в некоторых случаях, рекурсивный метод невероятно эффективен, если всё сделать правильно. Тем не менее, иногда лучше использовать циклы. Понимание обоих методов и умение эффективно их использовать поможет вам в работе и будет преимуществом на собеседовании.
Рекурсия и цикл, в чем разница? На примере Python
Цикл — это фундаментальный инструмент в программировании. Существует множество различных типов циклов, но почти все они выполнят одну базовую функцию: повторение определённых действий над данными, для их анализа или управления ими. Рекурсия, так же распространённый способ анализировать и манипулировать данными, как и цикл, но как правило, менее понятный и часто более запутанный. Почти все рекурсивные функции можно переписать в циклы, и наоборот. Тем не менее, каждый тип функции имеет свои преимущества и недостатки, и сегодня вы узнаете, в каких случаях применять тот или иной метод. В статье мы разберём следующие вопросы:
Начнём с метода, который кажется более простым из этих двух.
Циклы for
Цикл for используют для перебора последовательности данных (списка, кортежа, словаря, набора или строки). При достижении конца последовательности цикл завершается.
Например, вам нужно сложить числа от 1 до 5 и получить их сумму. Конечно, вы можете просто суммировать 1+2+3+4+5. Но, создать функцию намного удобнее, потому что вы сможете использовать её повторно, причём подставляя любые значения, даже если они не известны заранее.
Это будет выглядеть примерно так:
Для работы такого цикла, нам нужно хранить список всех чисел, чтобы мы могли перебирать элементы и складывать их в итоговое значение.
Вот как это выглядит в коде:
Запустив код, мы увидим, что все числа на своих местах и нам возвращается их сумма.
Вывод функции:
Рекурсия
Если функция вызывает сама себя, то это является признаком рекурсии. Одно из важнейших отличий рекурсии от цикла, это способ завершения рекурсивной функции. В приведённом выше примере цикл for завершается в конце последовательности, в которой он выполняется. А вот рекурсивная функция может продолжаться бесконечно, потому что она может не иметь последовательности данных. Вместо этого у рекурсивной функции есть так называемое базовое условие. Базовое условие определяет, когда цикл должен завершится.
Давайте попробуем решить предыдущую задачу рекурсивным способом. Визуально это выглядит так:
Каждый раз функция либо вызывает себя с новыми входными данными, либо возвращает значение.
Вот как это выглядит в коде:
Как видите мы передаём два значения: начальное и итоговое. При первом вызове функции итоговое значение равно 0, а начальное 5. Мы проверяем, является ли начальное число 0. Если нет, то вызываем функцию снова, но на этот раз мы меняем входное значение на 5–1 и 0+5, и повторяем этот процесс до тех пор, пока n не будет равно 0. После выполнения этого условия мы возвращаем итоговое значение (15).
Вычисление сложного процента рекурсией и циклом FOR
Давайте разберём более сложную задачу. Нужно определить стоимость кредита или инвестиции со сложным процентом. Чтобы это сделать, нам нужны следующие данные:
Формула расчёта сложного процента:
Так мы можем рассчитать всю сумму сразу. Но вместо этого, для расчёта мы используем цикл или рекурсию. В таком случае переменная времени (nt) будет обрабатываться в итерациях.
Давайте сразу создадим переменные, в которых будем хранить исходные числа и используем их в обоих методах:
Расчёт по сложной процентной ставке итеративно
Давайте сразу посчитаем общее количество платежей, чтобы упростить вычисление в цикле. Так как платежи ежемесячные, а количество лет равно 10, то результат будет 120, или 10*12. Теперь мы можем вычислять процент для каждого месяца и добавлять результат каждой итерации к основной сумме.
Так выглядит код:
Единственное различие между этим и предыдущим примерами заключается в том, что мы делаем на несколько вычислений больше во время каждой итерации. Также увеличилось число итераций с 5 до 120.
Результат наших вычислений:
Расчёт по сложной процентной ставке рекурсивным способом
В предыдущем примере последовательность данных равна 120, что отражает количество раз, когда основная сумма пересчитывается. Цикл прерывается по завершении последовательности. Рекурсивный метод позволяет нам поступить схожим образом, т.е. инициализировать счётчик и задать два условия.
Выполнить вычисление сложного процента. Добавить результат вычисления к общей сумме. Уменьшить значение счётчика на 1. Повторить те же действия, подставив новое значения для счётчика и общей суммы.
Возврат общей суммы
В предыдущем примере, цикл функции начинался со значения 5 и завершался при 0.
Здесь происходит тоже самое, только начальное значение теперь 120
Здесь мы либо снова вызываем функцию, либо возвращаем обновлённую общую сумму. Каждый раз вызывая функцию, значение счётчика уменьшается на 1. Возврат общей суммы происходит, когда счётчик равен 0.
Когда использовать рекурсию
Выбор между рекурсивным и итеративным методом может в значительной степени зависеть от языка, который вы используете, или от задачи, которую вы намерены решить. Например, в JavaScript рекурсия может привести к ошибкам stack frame errors, когда предел стека уже достигнут, а базовое условие ещё не выполнено. В таком случае, итеративный подход будет работать лучше.
Рассмотренный выше случай является хорошим примером того, когда рекурсия работает намного лучше, чем цикл.
Давайте представим, что помимо тех чисел, которые мы использовали в предыдущем примере, нам нужно учитывать и другие данные. Например, мы можем отслеживать то, как регулярные платежи влияют на срок кредита. Возможно, мы захотим остановить цикл до завершения последовательности. Если общее количество раз, когда начисляются проценты по кредиту равно 120, то и длина списка равна 120. Но, если сумма кредита будет равна 0 уже после 100 итераций, то в конце списка останется 20 неиспользуемых и ненужных элементов списка. Проблема дальнейшего усложнения сценария цикла заключается в том, что значения переменных, таких как сумма кредита, зависит от значения той же переменной на предыдущей итерации. Дело не в том, что это сложно реализовать, а в том, что это грязно.
Визуализация данной проблемы:
Рекурсивные структуры данных
Именно в таких случаях рекурсивные структуры данных особенно полезны. Структуру можно назвать рекурсивной, если её можно определить в терминах меньшей версии самой себя. Список является примером рекурсивной структуры данных.
Например, возьмём такой список:
Теперь, сделаем на его основе два меньших списка:
Если вывести оба списка, то мы увидим следующее:
Благодаря рекурсивным функциям и рекурсивными структурам данных мы можем изменить весь список или меньшую часть большего списка за раз. Итеративный подход решения подобной проблемы, позволяет изменить только одно значение в одном индексе за раз.
Пример того, как это сделать:
Сохранив маленькие части большого списка, мы можем вызвать ту же функцию (рекурсия) и отправить ей эти части (рекурсивная структура данных).
Вот как это работает на примере с вычислением сложного процента:
Наша функция в основном состоит из операторов if и else. Мы можем усложнить эту структуру если понадобится, но она и в таком виде делает всё что нам нужно. В итоге, мы хотим вернуть окончательные данные, которые покажут нам сумму кредита и размер текущего платежа на каждой итерации, когда начисляется процент.
Выходные данные:
Визуализация процессов рекурсивной функции:
При каждом рекурсивном вызове мы будем брать первый элемент массива из списка. Затем мы изменим значения этого элемента и снова вызовем функцию, но на этот раз передадим ей в качестве параметров array[:1] и array[1:]. На картинке видно, что, достигнув середины списка, мы будем иметь две его части одинакового размера. А уже к концу мы полностью переберём и модифицируем все элементы первого списка, и добавим их во второй список. Далее мы шаг за шагом реализуем эту функцию в коде.
Шаг 1: создаём массив
На данном этапе, наш массив имеет длину равную числу раз, когда начисляется процент. Каждый элемент содержит одинаковые данные, которые мы будем изменять рекурсивно.
Шаг 2: создаём функцию и базовое условие
Базовое условие будет учитывать два возможных сценария. Либо счётчик достигнул конца последовательности ( len(inputArr) == 0 ), либо мы погасили кредит раньше ( inputArr[-1][‘principal amount’] ).
Шаг 3: создаём выражение else и определяем переменные current, inputArray и outputArray
Шаг 4: если массив outputArray пуст, то берём первый элемент из массива входных данных и помещаем его в массив выходных данных без изменений.
Теперь оба массива выглядят как на картинке, которую вы видели выше, в момент первого вызова рекурсивной функции.
Шаг 5: если массив выходных данных не пуст, то изменяем все значения текущего элемента.
Шаг 6: добавляем переменную newCurrent к массиву outputArray
Шаг 7: вызываем рекурсивную функцию с новыми параметрами
Мы закончили! Так выглядит код целиком:
Чтобы убедиться, что код работает так, как мы задумали, давайте увеличим сумму платежа.
Если изменить сумму платежа на 2000, то при выводе должны получиться такие данные:
Такой код возвращает более чистый результат, чем при использовании цикла. Если бы мы использовали итеративный подход, то нам пришлось бы перебрать все 120 элементов, большинство из которых были бы бесполезны/пусты.
Заключение
На первый взгляд рекурсия может показаться сложной. Но в некоторых случаях, рекурсивный метод невероятно эффективен, если всё сделать правильно. Тем не менее, иногда лучше использовать циклы. Понимание обоих методов и умение эффективно их использовать поможет вам в работе и будет преимуществом на собеседовании.