чем определяются чаще всего амплитуды колебаний на роторных частотах
Добрый день коллега! Представляю вашему вниманию вторую статью, которая посвящена практическому анализу критических скоростей и собственных форм колебаний роторных машин.
Целью этой статьи является практическое понимание основных понятий, поведения колебания вала в роторной машине, основанное на визуальном представлении этих колебаний и изучении результатов воздействий этих колебаний на машину. Надеюсь, что это статья поможет неспециалисту лучше понять то, что происходит в машине, а специалист сможет получить другое представление об этом и на основе ранее неизвестных ему примеров.
Инженера, незнакомого с некоторыми из особенностей вибраций вращающейся машины, ее поведением при эксплуатации, изложенная в статье информация может сильно поразить. Как и в большинстве сфер профессиональной деятельности, по рассматриваемой нами теме имеется большое количество превосходной информации, из которой порой бывает очень трудно быстро найти информацию необходимую для практического применения, и которая позволила бы специалисту проникнуть в суть проблемы. С другой стороны с помощью анализа спектра вибрации можно определять большое количество неисправностей машины, которые сосредоточены на идентификации проблем и их особенностях, но при этом такой анализ не позволяет определить основную проблему, то есть не отвечает на вопрос: Что явилось первопричиной колебаний, а что является ее следствием?
Изучение этих вопросов основанных на проведении исследований и анализе колебаний приводят к возможности сделать попытку глубже заглянуть в суть основных характеристик колебаний роторных машин, используя минимум математических доказательств.
Таким образом, мы с вами обсудим несколько проблем, которые являются основными для понимания вибрации роторной машины, и ответим на следующие вопросы:
Знания вибрации, основанные на интуиции
Некоторые элементы конструкции совершают колебания с большей амплитудой, чем другие (например: по сравнению с металлическим прутом деревянная палочка). Мы интуитивно понимаем, какой предмет или элемент конструкции будет больше вибрировать или совершать перемещения назад — вперед с 
Например, качели с длинными верёвками совершают движения назад-вперед медленнее, чем качели с короткими веревками. При определении на качели воздействия силы определенной величины, заставляет, их перемещаться назад-вперед, что позволяет вам раскачиваться все выше и выше, при этом частота колебаний может быть выше или ниже собственной частоты колебаний качели.

Краткий обзор о Вибрации Элементов конструкции машины
Как инженеры, мы знаем, что вибрационные характеристики определяются массой конструкции, ее жесткостью и демпфированием (способность рассеивания колебательной энергии), которые играют главную роль, при контролировании амплитуды колебаний. Рассмотрим самую простую колебательную систему (рис.1), состоящую из массы (М), закрепленной на пружине, жесткость которой — К.
Рис.1 Простейшая колебательная система «масса-жесткость»
С помощью этой простой системы мы можем определить частоту колебаний (помня, что объекты большой массы имеют собственную частоту колебания на низких частотах, а объекты, имеющие высокую жесткость, имеют собственную частоту колебания на высоких частотах). После некоторой работы системы, мы делаем вывод, что собственная частота колебаний системы определяется как квадратный корень из соотношения жесткости системы (К) к ее массе (М).
Если мы сместим массу вниз и отпустим ее, то мы можем определить перемещение массы, совершаемые на одной частоте, подчиняющиеся закону синуса(рис.2) и которые равны собственной частоте колебаний (1).
Рис.2 Свободные колебания простейшей колебательной системы «масса-жесткость»
Добавим к нашей системе с одной степень свободы (рис.1) параллельно пружине демпфирующий элемент и приложим периодическую внешнюю силу, подчиняющей гармоническому закону (Рис.3).
Рис.3 Простейшая колебательная система «масса-жесткость-демпфирование»
Прикладывая периодическую силу постоянной величины, которая медленно увеличивается по частоте и записывая амплитуду перемещения, мы можем получить нормированные частотные характеристики классической системы «масса-жесткость-демпфирование». Повторяя тест с различными демпферами (амортизаторами), классическая частотная характеристика, показанная на рисунке 4, будет изменяться. Если мы знаем массу, жесткость и демпфирование нашей системы, то отклик ее вполне можно предсказать с помощью стандартного решения дифференциального уравнения движения этой системы (2).
Рис.4 Частотная характеристика системы «жесткость-масса-демпфирование»
На амплитудочастотной характеристике (рис.4) имеется несколько примечательных точек, которые заслуживают внимания. Первая заключается в том, что при низких частотах возбуждения, амплитуда колебаний почти не изменяется и больше нуля.
Максимальное значение достигается на частоте приблизительно равной собственной частоте затухающих колебаний (более технически правильно сказать — это пиковое значение амплитуды, возникающее на собственной частоте колебаний системы, как при минимальном ее демпфировании, так и при максимальном). Иногда говорят, система “в резонансе”, то есть когда частота возбуждения равна собственной частоте системы. Амплитуда колебаний достигает очень больших значений, если частота возбуждения близка к этой частоте. Амплитуда зависит от величины демпфирования (при максимальном — амплитуда уменьшается). При максимальном демпфировании на частотной характеристике (рис.4) нет никакого реального пика, в таких случаях говорят, что система сильно демпфирована. Далее, с увеличением частоты возбуждения амплитуда продолжает уменьшаться. Эти свойства частотных характеристик будут наблюдаться и на вращающихся системах, при ее неуравновешенности, о которых мы поговорим позже.
Переход от простой одно массовой системы к много массовой системе, основных положений не меняют. Собственные частоты по-прежнему в первую очередь связаны с массой и жесткостью системы, с некоторыми изменениями демпфирования. При равенстве частоты возбуждения, с собственной частотой системы, возникает резонанс системы. Возбуждение вблизи резонанса может вызвать очень большое увеличение амплитуды. Величина амплитуды изменяется при изменении демпфирования системы.
При больших значениях демпфирования пик амплитуды колебаний может быть полностью устранен. Самое главное изменение заключается в том, что теперь мы имеем многократные собственные частоты и каждая собственная частота имеет соответствующую ей собственную форму колебаний (мода) для различных частей конструкций, вибрирующих с различными амплитудами и отличающихся по фазе друг относительно друга.
Реальные конструкции можно приближенно рассматривать как серию очень малых распределенных масс, которые приближаются к сплошной распределённой массе. У непрерывной конструкции есть бесконечное число собственных частот, каждая из которых имеет характерную, только ей, собственную форму колебаний (моду).
Для примера рассмотрим простую балочную конструкцию, каждый конец которой шарнирно закреплен. Эта конструкция достаточно проста, а замкнутая ее форма позволяет рассчитать собственные частоты и формы (моды) колебаний балки. Ниже приведено уравнение (3) для расчета собственных частот колебаний. На рисунке 5 показаны первые три формы (мод) колебаний балки.
Рис.5 Первые три собственные формы колебаний балки
Если внимательно посмотреть на уравнение (3), то увидим, что это уравнение — все еще квадратный корень из соотношения жёсткости к массе элемента конструкции. Формы колебаний, показанные на рисунке 5 и далее в статье, являются собственными формами колебаний балки, в положении максимального ее смещения для заданной податливости (демпфирования). Пунктирные линии показывают промежуточные положения балки во время одного периода колебаний.
Все выше перечисленные основные положения можно перенести на различные вращающиеся машины, которые имеют несколько важных отличий, особенно, при вращении ротора.
Простая роторная машина
Роторные машины эквивалентны системе «жесткость-масса-демпфер», которая является системой с сосредоточенными массами на невесомом упругом валу. Рассмотрим такую модель ротора, которая представляет собой систему с одной степенью свободы, и обычно используется для изучения динамических характеристик ротора. Для целей настоящей статьи, будем использовать более сложную физическую модель ротора с несколькими степенями свободы. Такая модель показана на рис.6, которая состоит из жесткого диска, насаженного на вал посредине (имеющего жесткость и массу), опирающийся на два жестко закрепленных подшипника. Чтобы сделать пример более конкретным, на рисунке указаны габаритные размеры этой модели. Физически, эта модель чем-то похожа на ротор вентилятора, насоса или турбины.
Рис.6 Основная модель роторной машины для моделирования
Как определить резонанс роторной машины?
Рубрики: (Новости, вибродиагностика) Автор: Сергей Бойкин 27 Апр 2013
Теги : амплитудо-фазочастотная характеристика, амплитудочастотная характеристика, вибрация, вибрация машин, диапазон частот, колебательная система, метод ударного воздействия, резонанс, резонансная частота, тест-удар, частота колебаний
Добрый день коллега! Учитывая многочисленные просьбы рассказать о диагностике резонанса элементов машины, критических скоростях и о собственных формах колебаний ротора, я решил написать несколько статей посвященным этим вопросам.
В первой статье я расскажу о резонансе элементов и узлов машины. В ней мы с вами рассмотрим следующие вопросы:
Что такое Резонанс?
Большинство сооружений и машин совершают собственные колебания, поэтому периодические внешние воздействия на них могут вызвать резонанс. Резонансом часто называют колебания с собственной частотой или на критической частоте. Резонанс — это явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к резонансным частотам, определяемым свойствами системы. Увеличение амплитуды колебаний — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы (ротор-опора). Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы.
Чем определяются чаще всего амплитуды колебаний на роторных частотах
Вы можете почитать другие статьи блога, воспользовавшись Картой Сайта.
Хотите получать новые статьи прямо на Ваш почтовый ящик?
Любая механическая система может совершать колебания относительно положения равновесия. Свойства колебательной системы определяется набором собственных колебаний, каждое из которых называют модой и характеризуются тремя основными параметрами – собственной частотой, формой и коэффициентом потерь. Полный анализ колебательных свойств механической системы часто называют модальным анализом. Модальный анализ является одним из важных разделов вибродиагностики оборудования.
Чтобы изучить собственные колебания их нужно возбудить. Существует два основных способа возбуждения таких колебаний.
При разработке новых машин и оборудования используют оба вида возбуждения и анализа собственных колебаний.
При эксплуатации оборудования чаще всего используется наиболее простой импульсный метод возбуждения свободных колебаний, причем определяется, в основном, собственные частоты и коэффициенты затухания свободных колебаний на этих частотах, а форме колебаний уделяется значительно меньше внимания.
На практике для анализа вынужденных колебаний необходим источник колебательных сил. Если закрепить такой источник (вибратор, рис.1) на исследуемую механическую систему (опору, ротор, корпус и т.п.), он может существенно изменить колебательные свойства системы. Учет этих изменений сложен, поэтому гораздо чаще используется импульсное (ударное) возбуждение колебательной системы и анализируются ее свободные затухающие колебания.
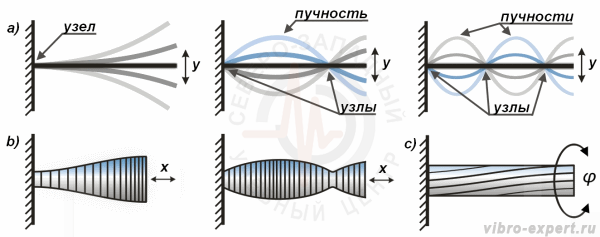
Деформируемые тела можно рассматривать, как колебательную систему с распределенными параметрами. В качестве примера можно рассмотреть колебания стержня, закрепленного в одной неподвижной точке (рис.2). Основными видами собственных колебаний стержня являются поперечные, продольные и крутильные колебания.
Форма колебаний деформируемых тел характеризуется дополнительными терминами – «узел» и «пучность». Узлами являются точки, в которых амплитуда колебаний определенной моды близка к нулю. Пучностями являются точки между узлами или на свободных концах, где амплитуда колебаний максимальна.
Максимальные собственные частоты имеют колебания простой формы (низкой моды). Они же, как правило, характеризуются и минимальными потерями, то есть затухают гораздо медленнее. Поэтому анализ собственных колебаний систем с распределенными параметрами заключаются, прежде всего, в определении основных характеристик простейших форм колебаний.
Эффективность анализа собственных колебаний при импульсном (ударном) возбуждении сильно зависит от особенностей ударного возбуждения, то есть от формы и точки действия ударного импульса. Лучшим местом и направлением удара при анализе собственных колебаний выбираемой исследователем формы является точка в зоне пучностей колебаний и направление, в котором эти колебания будут иметь максимум.
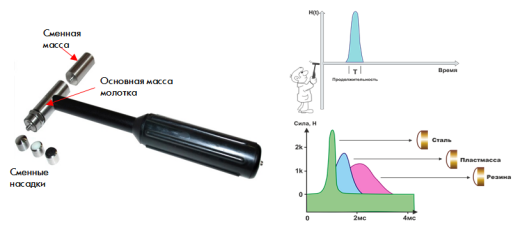
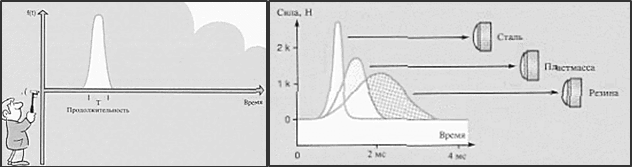
Колебания, создаваемые при ударе, представляют собой переходный, кратковременный процесс передачи энергии. Спектр ударной силы является непрерывным, с максимальной амплитудой при 0Гц и с последующим ее уменьшением с ростом частоты. Продолжительность удара, а, следовательно, и форма спектра при ударном возбуждении, определяется массой и жесткостью ударного молотка, так и конструкцией механической системы.
В практических задачах вибрационной диагностики машин и механизмов чаще всего исследуются собственные колебания простейших форм, в которых узлы и пучности определяются конструкцией машины (узла) и точками ее крепления к фундаменту, поэтому практически не изменяют своих координат при появлении дефектов. Собственная частота таких колебаний может изменяться в небольших пределах при изменении жесткости колебательной системы из-за дефектов узлов крепления, появления трещин и т.п. наибольшие относительные изменения при ухудшении состоянии оборудования имеют место у коэффициента потерь при колебаниях простейших форм тех элементов оборудования, которые выполнены из металла или других твердых материалов.
В частности, по скорости затухания свободных колебаний можно контролировать состояние валов, рабочих колес, отдельных лопаток, различных литых деталей и т.п., имеющих в бездефектном состоянии очень малые потери.
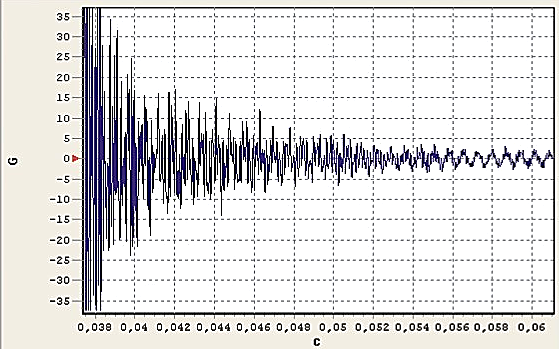
На эффективность вибрационной диагностики, на скорость затухания свободных колебаний влияет выбор способа крепления испытуемой конструкции и направление возбуждения колебаний. При выходном контроле простейшей детали или конструкции из твердых материалов крепить их следует в точках, удаленных от пучностей колебаний, то есть по возможности в узлах колебаний. Элементы крепления должны быть жесткими, без материалов, хорошо поглощающих вибрацию. Возбуждать колебания следует в точках, где имеются узлы других форм колебаний системы, затрудняющих определение скорости затухания исследуемой формы колебаний. Поскольку более высокие формы колебаний затухают быстрее колебаний простейших форм, при анализе последних целесообразно вводить задержку на время затухания высокочастотных колебаний. На рисунке 5 для примера показана форма колебаний корпуса машины при ударном возбуждении в момент времени t = 0, которая через небольшое время сохраняет только простейшие формы колебания.
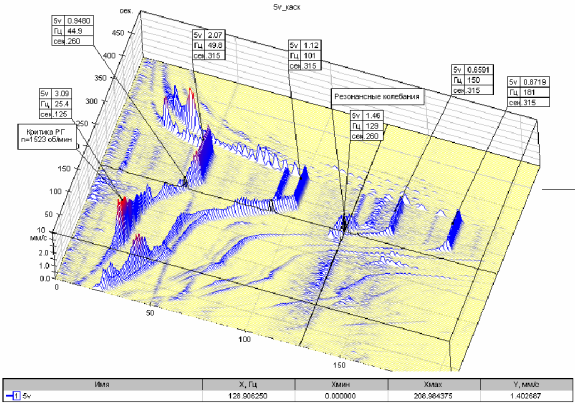
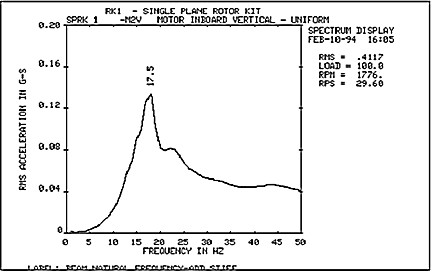
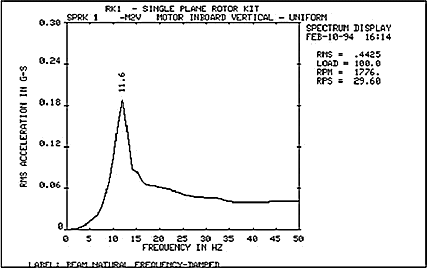
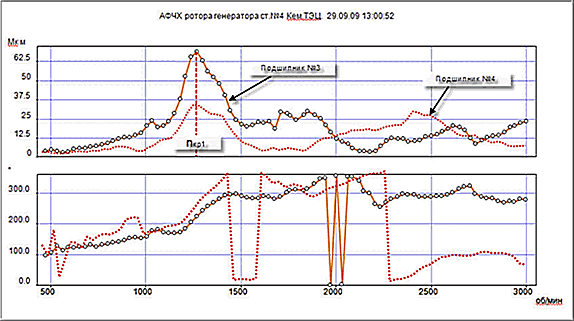
Для диагностики роторов многих машин по их собственным формам колебаниям достаточно часто используется естественный режим возбуждения вынужденных колебаний на собственных частотах — режим пуска (выбега) машины. В этом режиме колебательные силы на изменяющейся частоте вращения (или его гармониках) возбуждают резонансные колебания ротора и других узлов машины. Узкополосный синхронный анализ вибрации на частоте вращения ротора (или его гармониках) позволяет определить основные характеристики резонансных колебаний, такие как собственная частота и добротность резонанса (рис.6). В некоторых случаях эти характеристики оказываются непосредственно связанными с состоянием ротора или опор вращения.
Рис.6 График частотного спектра вибрации до 200Гц опоры генератора в вертикальном направлении на режимах пуска, холостого хода и останова ГТУ
Таким образом, анализ мод колебаний является эффективным экспериментальным методом определения динамических характеристик конструкций на основе результатов измерений и анализа вынужденных механических колебаний. Соединенные с анализатором датчик силы и акселерометр позволяют проводить одновременные измерения вынуждающей динамической силы и результирующих механических колебаний исследуемой конструкции. В результате обработки данных, осуществляемой анализатором, получается информация, необходимая для определения динамических характеристик исследуемой конструкции. Эта информация может быть использована для внесения изменений в конструкцию машины. Также этот метод может быть использован при мониторинге конструкций. В результате эксплуатации в машине могут происходить усталостные деформации, микротрещины в соединительных швах, которые не приводят к изменениям геометрических размеров изделия, но приводят к изменению динамических характеристик конструкции. Анализ этих изменений позволяет прогнозировать проведения регламентных работ по техническому обслуживанию. Этот метод эффективен в широкой области и используется при исследовании разного рода машин и конструкций от лопаток турбин до самолетов.
Чем определяются чаще всего амплитуды колебаний на роторных частотах
Вы можете почитать другие статьи блога, воспользовавшись Картой Сайта.
Хотите получать новые статьи прямо на Ваш почтовый ящик?
Добрый день коллега! Учитывая многочисленные просьбы рассказать о диагностике резонанса элементов машины, критических скоростях и о собственных формах колебаний ротора, я решил написать несколько статей посвященным этим вопросам.
В первой статье я расскажу о резонансе элементов и узлов машины. В ней мы с вами рассмотрим следующие вопросы:
Что такое Резонанс?
Большинство сооружений и машин совершают собственные колебания, поэтому периодические внешние воздействия на них могут вызвать резонанс. Резонансом часто называют колебания с собственной частотой или на критической частоте. Резонанс — это явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к резонансным частотам, определяемым свойствами системы. Увеличение амплитуды колебаний — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы (ротор-опора). Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы.
Параметры системы, такие, как низкая жесткость и/или слабое демпфирование, на резонансной частоте воздействуя на роторную машину, могут привести к возникновению резонанса. Резонанс не обязательно приводит к поломке машины или ее узла, за исключением, если дефекты в машине вызывают вибрацию или вблизи установленная машина, «наводит» вибрацию на той же частоте, что и собственные частоты.
Резонанс не создает вибрации, он только усиливает их. Резонанс это не дефект, а свойство механической системы. Поэтому, резонанс не вызывает проблем, если какие-либо колебания не возбуждают его.
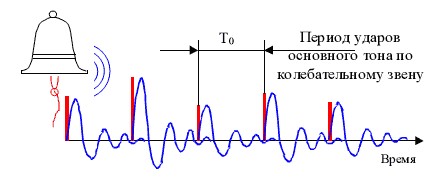
Это сопоставимо с колебаниями колокола, или барабана. В случае колебаний колокола (рис.1), вся его энергия содержится в потенциальной форме, когда он неподвижен и находится в верхних точках траектории движения, а при прохождении нижней точки на максимальной скорости, она преобразуется в кинетическую. Потенциальная энергия пропорциональна массе колокола и высоте подъёма относительно нижней точки, кинетическая — массе и квадрату скорости в точке измерения. То есть, если колокол ударить, то он будет резонировать с определенной частотой (или частотами). Если он находится в состоянии покоя, то он не будет совершать колебания на резонансной частоте.
Рис.1 Периодические колебания колокола
Резонанс — это свойство машины, когда она работает или не работает. Следует отметить, что динамическая жесткость вала при вращении машины может сильно отличаться, от статической жёсткости, когда машина не работает, при этом резонанс ее изменяется не существенно.
Есть такое неизменное правило, основанное на практическом опыте, которое гласит, что резонансные частоты, измеренные при останове (выбеге) машины меньше на 20 процентов частоты вынужденных колебаний. Резонансные частоты отдельных узлов и деталей машины, таких как вал, ротор, корпус, и фундамент — это колебания на их собственной частоте.
После монтажа машины резонансные частоты могут поменять свое значение из-за изменения параметров системы (массы, жесткости и демпфирования), которые после соединения всех механизмов машины в единый агрегат могут увеличиться или снизиться. Кроме того, динамическая жесткость, как отмечалось выше, может сдвинуть резонансные частоты, когда машины работают на номинальной частоте вращения. Большинство машин проектируются таким образом, чтобы ротор не имел собственную частоту колебаний такую же, как вал. Машина, состоящая из одного или двух механизмов не должна эксплуатироваться на резонансной частоте. Однако, при ее износе и изменении зазоров в машине, очень часто собственная частота смещается в сторону рабочей частоты вращения, вызывая резонанс.
Внезапное появление колебаний на частоте дефекта, таком как ослабление посадки или другого, могут вызвать колебания машины на резонансной частоте. При этом вибрация машины возрастет с допустимого уровня до недопустимого, если колебания вызваны резонансом узлов или элементов машины.
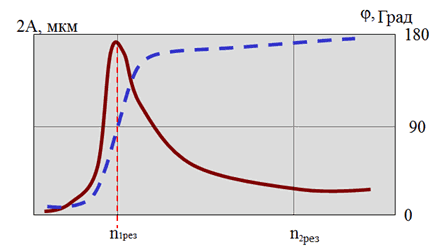
Рис.2 Амплитудо-фазочастотная характеристика ротора при пуске или останове машины
Например:
Двухскоростная машина работает при 900 об/мин и 1200 об/мин. Машина имеет резонанс на 1200 об/мин, который усиливает вибрацию на частоте вращения 1200об/мин. При 900 об/мин, вибрация составляет 2.54мм/с, а на 1200 об/мин резонанс увеличивает колебания до 12.7 мм/с
Рис.3 Справа колебания ротора имеющего одну плоскость коррекции (диск);
слева колебания сложной системы (двух соединенных роторов).
Сдвиг фаз на 180 градусов часто наблюдается только на роторах имеющих одну единственной плоскость коррекции (рис.3, слева). Более сложные системы «вал/ротор-опора» (рис.3 справа) имеют сдвиг фаз, который находится в пределах 1600 — 180 градусов. Всякий раз, когда специалист по анализу вибрации наблюдает высокую амплитуду колебаний, он должен предполагать, что рост ее до недопустимого уровня, возможно, связан с резонансом системы.
Масса, Жесткость и Демпфирование
Масса, жесткость, и демпфирование – это три параметра колебательной системы, которые воздействуют на частоту и увеличивают амплитуду колебаний при резонансе.
Масса – характеризует свойства тела и является мерой его инерции (чем больше масса тела, тем меньше ускорение оно приобретает под действием периодической силы), которое вызывает его колебания.
Жесткость – свойство системы, которое препятствует силам инерции возникающих в результате действия массовых сил.
Демпфирование – свойство системы, которое уменьшает энергию колебаний путем превращения ее в тепловую энергию вследствие трения в механической системе.
Для уменьшения резонанса параметры системы подбирают так, чтобы ее резонансные частоты располагались как можно дальше от возможных частот внешнего воздействия, для этого в практике используют так называемые динамические гасители колебаний, или демпферы.
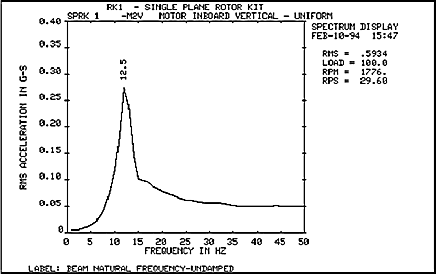
Рис.4 Амплитудочастотная характеристика (АЧХ) простейшей колебательной системы состоящей из массы, пружины и демпфера
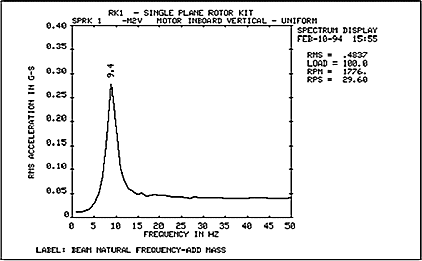
Увеличивая массу конструкции, уменьшается резонансная частота (рис.5).
Рис.5 АЧХ колебательной системы масса, которой больше, чем у системы, показанной на рис.4
Увеличивая жесткость конструкции, увеличивается резонансная частота (рис.6).
Рис.6 АЧХ колебательной системы жесткость, которой больше, чем у системы, показанной на рис.4
Увеличивая демпфирование конструкции, уменьшается амплитуда резонанса (рис.7).
Демпфирование – это единственное свойство, которое управляет амплитудой вибрации при резонансе конструкции.
Рис.7 АЧХ колебательной системы, демпфирование которой меньше, чем у системы, показанной на рис.4
Увеличение демпфирования конструкции также немного снижает и резонансную частоту. Если увеличить массу конструкции уменьшится резонансная частота, если уменьшить массу, то, резонансная частота увеличиться. Аналогично, если увеличить жесткость конструкции увеличится частота резонанса, когда уменьшаем жесткость, резонансная частота уменьшается.
Аналогию можно провести со струной гитары. Чем сильнее натянуть струну на гитаре (больше жесткости), тем тон звука повышается (резонансная частота) до того момента пока струна не порвётся. Если использовать самую толстую струну (большая масса), то тон звука, издаваемый ею, будет ниже.
Измерение резонанса
Одним из наиболее распространенных методов измерения резонансной частоты конструкции является ударное возбуждение конструкции с помощью ударного молотка.
Воздействие на конструкцию, в виде входного удара вызывает в определенном частотном диапазоне небольшой величины возмущающие силы. Колебания, создаваемые при ударе, представляет собой переходный, кратковременный процесс передачи энергии (рис.8). Спектр ударной силы является непрерывным, с максимальной амплитудой при 0 Гц и с последующим ее уменьшением с ростом частоты.
Рис.8 Продолжительность удара и форма спектра при ударном возбуждении определяется жесткостью головки молотка
Продолжительность удара и форма спектра при ударном возбуждении, определяется массой и жесткостью как ударного молотка, так и конструкцией машины. При применении относительно небольшого молотка на твердой конструкции жесткость головки молотка определяет спектр. Головка молотка действует как механический фильтр. Путем выбора жесткости головки молотка можно выбирать исследуемый частотный диапазон.
Если фаза не изменяется при прохождении предположительного резонанса, то это увеличение амплитуды может быть связано со случайным возбуждением и не является резонансом ротора. В таких случаях в дополнение к замерам вибрации при развороте/выбеге машины рекомендуется выполнить «тест на удар».
При использовании многоканального виброанализатора можно с большой точностью определить резонанс конструкции, если измерять сигналы на входе и выходе из системы в одно и то же время, при этом необходимо контролировать фазу колебаний и когерентность, которые будут собраны за то же самое время. Когерентность — функция двойного канала, которая используется для оценки степени линейности между сигналами на входе и выходе системы. Это означает, что резонансные частоты можно идентифицировать значительно быстрее.
Некоторые соображения о резонансе машин
Резюме
В этом разделе обсуждалось влияние резонансных частот на вибрацию машины. Все конструкции и машины имеют резонансные частоты, но резонанс не влияет на машину, если нет частот, которые возбуждают его. Если вибрацию машины возбуждает ее собственная частота, то существуют три варианта отстройки системы от резонанса.
Варианты 2 и 3 обычно требуют некоторые изменения в конструкции, которые нельзя выполнить, если модальный анализ и/или изучение исследования конечного элемента не были выполнены на конструкции.