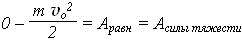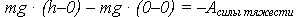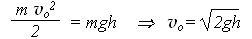чем определяется потенциальная энергия системы

Потенциальная энергия, ее определение, виды и формулы

Определение потенциальной энергии

Энергия, говоря простым языком, это возможность что-либо сделать, возможность совершить работу. То есть, если какое-либо тело может совершить какую-либо работу, то про это тело можно сказать, что оно обладает энергией. По сути, энергия — это мера различных форм движения и взаимодействия материи, а её изменение происходит при совершении некоторой работы. Таким образом, совершённая работа всегда равна изменению какой-либо энергии. А значит, рассматривая вопрос о совершённой телом работе, мы неизбежно приходим к изменению какого-либо вида энергии. Вспомним также и тот факт, что работа совершается только в том случае, когда тело под действием некоторой силы движется, и при этом сама работа определяется как скалярное произведение вектора этой силы и вектора перемещения, то есть А = F*s*cosa, где а — угол между вектором силы и вектором перемещения. Это нам пригодится в дальнейшем для вывода формул различных видов энергии.

Энергию, связанную с взаимодействием тел, называют ПОТЕНЦИАЛЬНОЙ ЭНЕРГИЕЙ. Иначе говоря, если тело за счёт взаимодействия с другим телом может совершить некоторую работу, то оно будет обладать потенциальной энергией, и при совершении работы будет происходить изменение этой энергии. Обозначают механическую потенциальную энергию чаще всего — Еп.

Виды потенциальной энергии

Существуют различные виды потенциальной энергии. К примеру, любое тело на Земле находится в гравитационном взаимодействии с Землёй, а значит обладает потенциальной энергией гравитационного взаимодействия. И ещё пример — витки растянутой или сжатой пружины находятся в упругом взаимодействии друг с другом, а значит сжатая или растянутая пружина будет обладать потенциальной энергией упругого взаимодействия.

Далее мы рассмотрим только виды механической потенциальной энергии и формулы, по которым их можно рассчитать. Но в дальнейшем вы узнаете и о других видах потенциальной энергии — к примеру, о потенциальной энергии электрического взаимодействия заряженных тел, о потенциальной энергии взаимодействия электрона с атомным ядром.

Формулы потенциальной энергии

Перед тем как приступить к выводу формул потенциальной энергии, ещё раз вспомним, что совершённая телом или над телом работа равна изменению его энергии. При этом, если само тело совершает работу, то его энергия уменьшается, а если над телом совершают работу, то его энергия увеличивается. К примеру, если спортсмен поднимает штангу, то он сообщает ей потенциальную энергию гравитационного взаимодействия, а если он отпускает штангу и она падает, то потенциальная энергия гравитационного взаимодействия штанги с Землёй уменьшается. Также, если вы открываете дверь, растягивая пружину, то вы сообщаете пружине потенциальную энергию упругого взаимодействия, но если потом дверь закрывается, благодаря сжатию пружины в начальное состояние, то и энергия упругой деформации пружины уменьшается до нуля.

А) Чтобы вывести формулу потенциальной энергии гравитационного взаимодействия, рассмотрим, какую работу совершает тело, двигаясь под действием силы тяжести:

А = F*s = mg*s = mg*(h₁ — h₂) = mgh₁ — mgh₂ = Eп₁ — Еп₂, то есть, мы получили, что потенциальная энергия гравитационного взаимодействия тела с Землёй может быть вычислена по формуле: Еп = mgh.

Здесь важно отметить, что поверхность Земли принимается за начало отсчёта высоты, то есть для тела, находящегося на поверхности Земли Еп = 0, для тела, поднятого над Землёй Еп > 0, а для тела, находящегося в яме глубиной h, Еп 2 /2 = 0 — kх 2 /2 = Еп₁ — Еп₂.

В итоге, мы получили формулу потенциальной энергии упругой деформации: Еп = kx 2 /2.

Методические советы учителям

1) Обязательно обратите внимание учащихся на связь энергии и работы.

2) Не давайте учащимся формулы потенциальной энергии без вывода.

3) Обратите внимание учащихся на то, что оба вида потенциальной энергии зависят от выбора начальной точки, то есть от системы координат.

4) При выводе формул потенциальной энергии обязательно поясните учащимся почему отсутствует cosa в формуле работы.

5) Отметьте, что и работа силы тяжести, и работа силы упругости не зависят от формы траектории и, следовательно равны нулю на замкнутой траектории — это общее и важное свойство всех потенциальных сил.

Источник

Беседа 2. Потенциальная энергия

Коллега, о потенциальной энергии, пожалуйста, поподробнее.

Вы, мой друг, совершенно правильно интересуетесь важнейшей составляющей полной энергии.

Принято считать, что потенциальная энергия является частью общей энергии системы, зависящей от взаимного расположения материальных частиц, составляющих эту систему, и от их положений во внешнем силовом поле (гравитационное, электрическое поле).

Силовым полем мы называем ту часть пространства, в каждой точке которой на помещенную туда материальную частицу действует определённая по величине и направлению сила.

Численно потенциальная энергия системы в данном её положении равна работе, которую произведут действующие на систему силы при её перемещении из этого положения в то, где потенциальная энергия равна нулю.

Коллега, энергией обладает только пробное тело в потенциальном поле или потенциальное поле тоже?

Для ответа на Ваш вопрос открываем БСЭ (Большая Советская Энциклопедия) и в разделе «Поля физические» читаем (дословно):
«Поля физические, особая форма материи; физическая система, обладающая бесконечно большим числом степеней свободы. Примерами полей физических могут служить электромагнитное и гравитационное поля. ».

Отсюда следует, что потенциальное поле является материальной средой. Значит, как и любая материальная среда, это поле обладает энергией (соответственно, и массой). Кстати, это подтверждается, к примеру, наличием в поле электромагнитных волн, которые являются колебаниями этой материальной среды.

Конкретные границы поля определить сложно, поэтому физики давно привыкли оперировать энергией, содержащейся в единице объёма, то есть – объёмной плотностью энергии потенциального поля (измеряется в Дж/м 3 ). Возьмём, к примеру, книгу Зильбермана «Электричество и магнетизм» (Наука, М., 1970) и на стр. 136 читаем (дословно):
«В плоском конденсаторе и вообще в однородном поле плотность энергии, т. е. энергия, содержащаяся в единице объёма, постоянна и равна полной энергии, делённой на объём».

Коллега, раз уж потенциальное поле является материальной средой, то оно должно характеризоваться конкретными параметрами, которые можно вычислить и измерить.

Вы совершенно правы. Мы уже выяснили, что электрическое (потенциальное) поле характеризуется таким параметром, как объёмная плотность энергии (далее – давление, Дж/м 3 или Н/м 2 ). Кроме этого, потенциальное поле характеризуется потенциалом и его градиентом – напряженностью поля. Причем, давление, потенциал и напряженность характеризуют потенциальное поле в данной его точке, независимо от наличия в этой точке пробного тела, ибо поле, как мы уже знаем, само обладает энергией и массой.

Если потенциальную энергию (W_П, Дж) отнести к единичной массе (m, кг) или к единичному электрическому заряду (q, Кл), то получим гравитационный (v 2 = W_П/m, Дж/кг) или электрический (U = W_П/q, Дж/Кл) потенциалы.

Градиентом потенциала в данной его точке является напряженность поля:
— для гравитационного поля: g = – grad v 2 ;
— для электрического: E = – grad U (о знаке речь пойдет ниже).

Градиент (от лат. gradiens, род. падеж gradientis – шагающий), вектор, показывающий направление наискорейшего изменения некоторой величины от одной точки пространства к другой.

С удалением от центра поля изменяется не только потенциал, но и потенциальная энергия. И её градиентом является сила, которую мы называем силой тяготения.

Уравнение F = – grad W_П показывает, что работа сил вдоль замкнутой траектории в потенциальном поле всегда равна нулю.

Коллега, какие единицы измерения наиболее приемлемы для вышеназванных параметров?

Очень хороший вопрос. СИЛА измеряется в ньютонах (Н = кг*м/с 2 ) или в Дж/м. Второй вариант записи более приемлемый, ибо сразу даёт нам указание на то, что сила является всего лишь ГРАДИЕНТОМ ЭНЕРГИИ (Дж/м). Это важно, ибо упрощает дальнейшее понимание физических процессов. Кстати, это касается не только силы, но и таких параметров, как давление и потенциал.

ПОТЕНЦИАЛ измеряется в м 2 /с 2 или в Дж/кг (для гравитационного поля) и в (кг/Кл)*( м 2 /с 2 ) или Дж/Кл (для электрического поля). И здесь более приемлемым является второй вариант записи, ибо сразу указывает на значение потенциальной энергии, отнесенной к единице массы (Дж/кг) для гравитационного поля или отнесенной к единице электрического заряда (Дж/Кл) для электрического поля.

И наконец, коллега, давайте рассмотрим, как определяется значение потенциальной энергии.

Пожалуй, теперь мы готовы решать и эту проблему. Значение потенциальной энергии определяется двумя способами:
— упрощенный (приближенный) – для однородного поля;
— общий (истинный) – для неоднородного поля, которое нас реально и окружает.

Потенциальное поле можно условно считать однородным, если вектор напряженности во всех его точках имеет одно и то же значение и направление. К примеру, для гравитационного поля это правило можно применить только у поверхности Земли на небольшом её участке (скажем, в лабораторном опыте). В этом случае для упрощения расчетов значение потенциальной энергии пробного тела на поверхности Земли условно принимается равной нулю, а её значение в любой другой точке определяется из уравнения:

W_П = mgh, Дж,
где g – напряженность гравитационного поля (Н/кг), а h – вертикальное расстояние (м) от поверхности Земли до пробного тела массой m (кг).

Здесь знак перед значением потенциальной энергии принципиального значения не имеет.

Коллега, но ведь это и есть наиболее распространенный способ определения потенциальной энергии.

К сожалению, многие учебники физики на этом и завершают определение потенциальной энергии. Но не все. Взять, к примеру, Общий курс физики Сивухина (Москва, МФТИ, 2005) или американский курс Физики в переводе под редакцией Ахматова (Москва, Наука, 1974).

Здесь рассматривается:
— уже известный нам способ определения потенциальной энергии пробного тела в однородном поле тяжести у поверхности Земли (том 1, стр. 144-145 первого источника и часть III, стр.152-157 второго источника);
— и общий способ определения потенциальной энергии для неоднородного поля (том 1, стр. 145-146 первого источника и часть III, стр.157-159 второго источника).

Общий способ расчета дает уже отрицательное значение потенциальной энергии:
— уравнение (25.6) W(U) = – GMm/r в первом источнике и
— уравнение W(Ur) = – GMm/r – во втором.

Отрицательное значение потенциальной энергии здесь объясняется следующим образом:
— в первом источнике (цитата): «Максимальной энергией притягивающиеся массы обладают при бесконечном расстоянии между ними. В этом положении потенциальная энергия считается равной нулю. Во всяком другом положении она меньше, т. е. отрицательна»;
— во втором источнике дано доказательство правильности уравнения W(Ur) = – GMm/r.

И действительно, свободно падающее к центру поля тело теряет свою потенциальную энергию, которая переходит в кинетическую. Значит, потенциальная энергия с уменьшением расстояния между центрами масс (M и m) уменьшается и, наоборот, с увеличением расстояния – увеличивается.

Учитывая, что в уже известном нам уравнении W_П = – GMm/r символ радиуса находится в знаменателе, то предельно ясно, что с увеличением расстояния (значение радиуса стремится к бесконечности) потенциальная энергия увеличивается до… нуля. Такое возможно только в том случае, если потенциальная энергия во всяком другом положении отрицательна.

Вывод: потенциальная энергия для всех материальных частиц отрицательна.

Отсюда следует, что значение гравитационного потенциала v 2 = W_П/m = – GM/r тоже отрицательно. И подтверждением этому является уравнение (3) в разделе «Тяготение» (стр. 772) Физического Энциклопедического Словаря или аналогичного раздела Большой Советской Энциклопедии.

Аналогично определяется значение потенциальной энергии и электрического потенциала в электрическом поле. Причем далее мы убедимся в том, что потенциальная энергия и её объёмная плотность (давление) ОДИНАКОВЫ и для гравитационного, и для электрического полей.

Коллега, теперь попробуйте записать Ваше высказывание в виде формулы.

Формулы пишут математики, а физики пользуются уравнениями. Необходимые уравнения здесь уже приводились. Однако попробуем, все же, обойтись пока без них, тем более – без «формул».

Для этого используем бытовые наблюдения, которые подсказывают: чтобы испарить воду, кипящую в чайнике, нужно сжечь некоторое количество дров или газа. Другими словами, нужно совершить работу. С помощью термометра можно убедиться, что температура кипящей воды и температура пара над ней одинаковы. Следовательно, одинакова и средняя энергия движения частиц в кипящей воде и в паре.

Вывод: тепловая энергия, передаваемая кипящей воде от топлива, преобразуется в энергию взаимодействия частиц испаряющейся воды. Значит, энергия связи частиц в кипящей воде меньше, чем в водяном паре. Но в паре эта энергия практически равна нулю, следовательно, энергия взаимодействия частиц в жидкости меньше нуля, т.е. отрицательна.

Коллега, Ваши доводы убедительны и примеры Вы приводите неопровержимые. Однако не все думают так же.

Однако математики так не думают. Для них гравитационное поле является ОДНОРОДНЫМ с неизменной напряженностью гравитационного поля (вроде этот параметр и не зависит от радиуса). Значение потенциальной энергии они определяют по упрощенной формуле W = mgh. Они не связывают h с радиусом поля, а считают его простым отрезком между двумя произвольными точками этого поля. Поэтому для них потенциальная энергия может принимать нулевое значение в любой понравившейся им точке. Нонсенс, но бывает и такое.

Но есть ещё и «физико-математики». Их мнение зависит от того, насколько они физики или математики.

Коллега, почему Вы считаете, что математики «тяготеют» к однородному полю?

В подтверждение этому открываем Краткий курс математического анализа (Бермант, Араманович, 2005) и на стр. 520 в разделе «Теория поля» читаем:
«Векторное поле называется однородным, если А(Р) — постоянный вектор, т.е. Ах, Аy и Az — постоянные величины.
Примером однородного поля может служить, например, поле тяжести».

Теперь Вы и сами видите, что математики гравитационное поле называют «полем тяжести» и «всерьёз» считают его однородным. И это не просто безобидное заблуждение, ибо оно мешает нам осознать Природу гравитации. Однако, об этом мы поговорим немного позже.

Источник

Потенциальная энергия.

Потенциальная энергия – энергия взаимодействия тел. Потенциальной энергией тело само по себе не может обладать. Потенциальная энергия определяется силой, действующей на тело со стороны другого тела. Поскольку взаимодействующие тела равноправны, то потенциальной энергией обладают только взаимодействующие тела.

Какова работа, совершаемая силой тяжести при перемещении тела массой m вертикально вниз с высоты h₁ над поверхностью Земли до высоты h₂. Если разность h₁ – h₂ пренебрежимо мала по сравнению с расстоянием до центра Земли, то силу тяготения во время движения тела можно считать постоянной и равной .

Поскольку перемещение по направлению совпадает с вектором силы тяжести, то работа силы тяжести равна:

Теперь рассмотрим движение тела по наклонной плоскости. При перемещении тела вниз по наклонной плоскости сила тяжести совершает работу

Из рисунка видно, что scosα = h, следовательно

Выходит, что работа силы тяжести не зависит от траектории движения тела.

Т. е. работа силы тяжести при перемещении тела массой m из точки h₁ в точку h₂ по любой траектории равна изменению некоторой физической величины mgh с противоположным знаком.

Физическая величина, равная произведению массы тела на модуль ускорения свободного падения и на высоту, на которую поднято тело над поверхностью Земли, называется потенциальной энергией тела.

Потенциальную энергию обозначают через Е_р. Е_р = mgh, следовательно:

Тело может обладать как положительной, так и отрицательной потенциальной энергией. Тело массой m на глубине h от поверхности Земли обладает отрицательной потенциальной энергией: Е_р = – mgh.

Рассмотрим потенциальную энергию упругодеформированного тела.

Прикрепим к пружине с жесткостью k брусок, растянем пружину и отпустим брусок. Под действием силы упругости растянутая пружина приведет в действие брусок и переместит его на некоторое расстояние. Вычислим работу силы упругости пружины от некоторого начального значения x₁ до конечного x₂.

Сила упругости в процессе деформации пружины изменяется. Чтобы найти работу силы упругости можно взять произведение среднего значения модуля силы и модуля перемещения:

Так как сила упругости пропорциональна деформации пружины, то среднее значение ее модуля равно

Подставив это выражение в формулу работы силы, получим:

Физическую величину, равную половине произведения жесткости тела на квадрат его деформации, называют потенциальной энергией упругодеформированного тела:

Как и величина mgh, потенциальная энергия упругодеформированного тела зависит от координат, поскольку x₁ и x₂ – это удлинения пружины и в то же время – координаты конца пружины. Поэтому можно сказать, что потенциальная энергия во всех случаях зависит от координат.

Источник

Потенциальная энергия механической системы

Вы будете перенаправлены на Автор24

Потенциальной энергией называют вид механической энергии системы тел, которая определена силами взаимодействия между телами и их взаиморасположением.

Допустим, что взаимодействие тел реализуется посредством потенциальных полей.

Свойства потенциальности поля означают, что:

Работа в потенциальном поле

Далее мы будем использовать следующую теорему:

Мы знаем, что работу силы можно вычислить, в соответствии с формулой:

$\Delta E_k= \int_1^2 \vec F d\vec s =A(2),$

$dA=\vec F d\vec s=F_x dx+F_y dy+F_z dz (3).$

Учитывая теорему (1), формулу (3) представим как:

Из теории функции мы знаем, что дифференциал функции равен:

Готовые работы на аналогичную тему

Тогда формула элементарной работы будет записана как:

Если формулу (6) проинтегрировать, то получится работа, при перемещении материальной точки из положения 1 в положение 2:

$A_<12>=\int_1^2 dU=U_1-U_2 (7).$

Формула (7) указывает на то, что работа в нашем случае (случае консервативных сил) зависит только от начальной и конечной точек траектории и не зависит от вида траектории.

Сравнивая выражения (2) и (7), получаем:

$\Delta E_k=-\Delta U (8).$

Выражение (8) удобно записать в виде:

Сумма кинетической и потенциальной энергии остается неизменной величиной при движении материальной точки в потенциальном поле.

Нормирование потенциальной энергии

Выше потенциальная энергия определена нами как функция, частные производные которой по координатам, берущиеся со знаками минус, равны соответствующим составляющим силы (формулы 1).

Если рассмотреть какую-либо пространственную точку, то можно предположить, что потенциальная энергия в этой точке есть заданная величина. Следовательно, физическим смыслом обладает не сама величина потенциальной энергии, а ее изменение при переходе от одной точки к другой.

Используя произвол в выборе потенциальной энергии, можно задать ей любое значение в некоторой пространственной точке. В этом случае для всех остальных точек величина потенциальной энергии станет фиксированным однозначно. Данную процедуру придания потенциальной энергии однозначности назвали нормировкой.

Потенциальная энергия тела, поднятого над земной поверхностью

Рисунок 1. Потенциальная энергия тела, поднятого над земной поверхностью. Автор24 — интернет-биржа студенческих работ

Запишем составляющие силы, которая действует на нашу материальную точку (рис.1):

$F_x=0; F_y=0; F_z=-mg (11),$

Тогда потенциальную энергию в соответствии с формулой (1) запишем как:

Энергия взаимодействия

Наличие потенциальной энергии у тела вызвано его взаимодействием с другими телами. При отсутствии взаимодействия, потенциальная энергия равна нулю.

Силу тяготения можно считать неизменной только недалеко от поверхности Земли.

Источник

Потенциальная энергия

В 7 классе мы узнали, что тело может обладать потенциальной энергией потому, что взаимодействует с другими телами или частями одного и того же тела (см. § 5-д). Теперь дополним, что потенциальная энергия различных видов вычисляется по следующим формулам:

При действии Fтяж	При действии Fупр

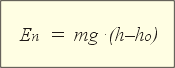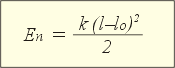В левой формуле есть «нулевое» значение высоты, а в правой – «нулевое» значение длины упруго деформированного тела. Другими словами, значение потенциальной энергии зависит от выбора нулевого уровня энергии.

Почему именно так вычисляют различные потенциальные энергии тел? Оказывается, что если пользоваться этими формулами, начинает выполняться теорема об изменении потенциальной энергии:

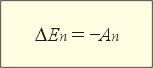DEп – изменение потенциальной энергии тела, Дж Aп – работа потенциальной силы, Дж

Эта теорема читается так: изменение потенциальной энергии тела равно взятой с противоположным знаком работе потенциальной силы, действующей на тело. Эта теорема применяется и доказазывается только для потенциальных сил – зависящих от положения тел (или частей тела) и не зависящих от траектории, по которой тело (или части тела) совершают перемещение из начального положения в конечное.

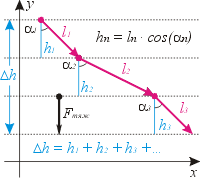
Поясним, какие силы будут потенциальными. Рассмотрим силу тяжести. Пусть она скатывает тело по склону с многочисленными изломами. Их можно считать множеством наклонных плоскостей, механическая работа на каждой из которых равна mg·ln·cos( a n) = mg·hn. В этой формуле ln – длина n-ой «плоскости», hn – её высота, a n – угол между векторами силы и перемещения.

Полная работа силы тяжести будет равна сумме:

Aтяж = mgh1 + mgh2 + … + mghn = mg ·(h1+h2+…+hn) = mg·Dh

Это равенство показывает, что работа силы тяжести зависит только от изменения положения тела и не зависит от формы и/или длины траектории движения тела. Поэтому сила тяжести – всегда потенциальная сила. Работа архимедовой силы тоже не зависит от траектории движения тела в среде, следовательно, архимедова сила – всегда потенциальная сила (если, конечно, среда однородна и тело всё время погружено целиком).

Вспомним, что сила упругости может как не подчиняться закону Гука (если деформация не упругая), так и подчиняться ему. В случае, если сила упругости подчиняется закону Гука, она потенциальна.

Работа силы трения скольжения зависит от формы и/или длины траектории тела, поэтому сила трения скольжения никогда не будет потенциальной. Работа силы трения покоя всегда обращается в ноль при возврате в исходную точку, значит, сила трения покоя – всегда потенциальная сила.

Формулы и теорема о потенциальной энергии легко проверяются опытами, одним из которых может быть следующая задача.

Задача. Из вертикальной пружинной пушки выстреливают шар, и он поднимается на высоту 1 м. Какую скорость шар имел при вылете?

Решение. Зная, что в верхней точке траектории скорость шара равна нулю, запишем теорему об изменении кинетической энергии:

В полёте на шар действует только одна и потенциальная сила – сила тяжести. Приняв за нулевой уровень потенциальной энергии точку вылета шара, запишем теорему об изменении потенциальной энергии:

Упростив равенства и решив систему двух уравнений, получим:

Ответ: начальная скорость шара при вылете из пушки была » 4,5 м/с.

Источник