чем обуславливается сопротивление взаимному перемещению частиц в сыпучих грунтах

Тест с ответами по землеустройству на тему Грунты

: Сжимаемость грунтов обусловлена изменением объема …

2: Сжатие грунта вызывают:

-: нейтральное давление и эффективные напряжения;

+: эффективное напряжение, то есть передающееся на скелет грунта;

-: напряжения не вызывают сжатие грунта.

3: Сжимаемость грунтов обусловлена:

-: изменением размера частиц;

+: изменением пористости вследствие переупаковки частиц;

-: ползучестью водных оболочек, вытеснением воды из пор грунта;

-: изменением пористости, ползучестью водных оболочек, вытеснением воды из пор.

4: Коэффициентом сжимаемости грунта называется …

-: тангенс угла наклона отрезка компрессионной кривой к оси коэффициента пористости

-: отношение изменения коэффициента пористости к начальному коэффициенту пористости

+: отношение изменения коэффициента пористости к модулю общих деформаций

-: тангенс угла наклона отрезка компрессионной кривой к оси уплотняющих давлений.

5: Прибор компрессионного сжатия одометр служит:

-: для определения прочностных характеристик грунтов;

+: для определения показателей деформируемости грунтов;

-: для определения степени влажности грунтов;

-: для определения физических характеристик грунтов.

6: Компрессионная кривая это:

-: кривая зависимости осадки от нагрузки;

-: кривая зависимости осадок во времени;

: кривая зависимости деформаций от напряжений в грунтах;

+: кривая зависимости коэффициента пористости от нормальных напряжений.

7: Уравнение компрессионной кривой

8: Коэффициент Пуассона это:

-: приращение бокового давления к приращению вертикального давления;

+: отношение боковых деформации к вертикальным деформациям;

-: отношение бокового давления к площади образца;

-: отношение бокового давления к объему образца.

10: Независимые характеристики сжимаемости:

-: модуль общей деформации;\

+: модуль общей деформации и коэффициент Пуассона;

-: модуль общей деформации, коэффициент Пуассона, относительная сжимаемость;

-: модуль общей деформации, коэффициент Пуассона, относительная сжимаемость, коэффициент бокового расширения.

11: Стабилометр это:

+: прибор для определения прочностных и деформационных характеристик грунта;

-: прибор для проведения статического зондирования;

-: прибор для измерения шероховатости дна котлована;

-: прибор для наблюдения за осадками сооружений.

12: Сопротивление грунтов сдвигу зависит от …

-: характера развития деформаций сдвига

-: касательных напряжений в грунте

-: схемы приложения сдвигающей нагрузки

+: сил трения и сцепления в грунте.

13: Сопротивление взаимному перемещению частиц в пылевато-глинист ых грунтах обуславливается:

-: водно–коллоидным и связями;

-: кристаллизационн ыми связями.

14: Прочностные характеристики грунтов определяются с помощью:

+: прибора одноплоскостного среза и стабилометра;

-: прибора одноплоскостного среза;

-: прибора компрессионного сжатия.

17: С какой целью проводится метод зондирования грунта?

-: Для определения плотности грунта

-: Для определения прочности грунта

-: Для определения влажности грунта

-: Для определения гран. состава грунта.

18: Какая существует связь между коэффициентом относительной сжимаемости и модулем общей деформации?

19: В каких единицах измеряется коэффициент относительной сжимаемости грунта?

20: С какой целью проводятся компрессионные испытания грунтов?

21: Для какой цели служат штамповые испытания?

+ : Определение модуля деформации

-: Определение сжимаемости, модуля деформации, коэффициента фильтрации.

22: В каком диапазоне напряжений определяется коэффициент сжимаемости грунта?

+:  Р = дополнительное – природное (P _доп — P _q )

-:  Р = дополнительное + природное (P _доп +P _q )

23: Для какой цели служит обратная ветвь компрессионной кривой?

-: Для контроля испытаний

+ : Для определения разуплотнения грунта

-: Для определения разуплотнения и упругих свойств грунта

-: Для определения разуплотнения, упругих и остаточных свойств грунтов.

24: Чем обуславливается сжимаемость грунтов?

+ : Изменением пористости грунта вследствие переупаковки частиц, ползучестью водных оболочек, вытеснением воды из пор грунта

-: Разрушением минеральных частиц, удалением воздуха и воды из пор грунта

-: Фильтрацией воды, уплотнением минеральных частиц, ползучестью скелета грунта

-: Разрушением структурной прочности, выдавливанием грунта в стороны, вытеснением связной воды.

26: Что называется коэффициентом бокового давления грунта?

+: Отношение приращения бокового давления ∆σ _у к приращению вертикального давления ∆σ _х

-: Отношение относительной поперечной деформаций ε _х к продольной деформации ε _у

-: Отношение приращения деформаций ∆S к приращению напряжения ∆σ

-: Отношение изменение пористости ∆е к изменению давления ∆Р.

27: Назовите прочностные характеристики грунта и испытания, при которых они определяются?

28: С какой целью определяется угол внутреннего трения и сцепление грунта?

+: Для определения прочностных свойств грунтов

-: Для определения деформационных свойств грунтов

-: Для определения физических свойств грунта

-: Для определения деформационно-пр очностных свойств грунта.

29: В чём преимущества стабилометрическ их испытаний по сравнению со сдвиговыми?

-: Возможность определения формы деформации

-: Учёт объёмно – напряжённого состояния.

30: Какое минимальное количество образцов глинистого грунта необходимо для стабилометрическ их испытаниях?

31: Какие характеристики грунта определяются стабилометрическ ими испытаниями?

32: При стабилометрическ их испытаниях получили значения главных нормальных напряжений  ₁ = 0,15 МПа,  ₂ = 0,05 МПа. Определить угол внутреннего трения песка.

33: В каких единицах измеряется сцепление грунта?

34: Для чего служат испытания грунта крыльчаткой?

35: Какими испытаниями можно определить коэффициент Пуассона в грунтах?

Источник

Сайт инженера-проектировщика

Свежие записи

Сопротивление грунтов сдвигу. закон Кулона

Сопротивление грунтов сдвигу. закон Кулона

Под действием собственного веса или приложенной внешней нагрузки в отдельных точках (областях) массива грунта внешние эффективные давления могут вызвать касательные напряжения, превышающих внутренние связи в точках контактов структурных агрегатов и самых твердых частиц. В результате возникают оползни (скольжения) одних частиц и их агрегатов относительно других, что может нарушить целостность грунта в некоторой области, то есть прочность грунта будет исчерпана.

Характерными проявлениями сдвига является выпирание массивов грунта из-под подошвы фундаментов, сползания грунтовых массивов в откосах и склонах и тому подобное.

Внутреннее сопротивление, препятствует смещению частиц в сыпучих (несвязные) грунтах, т.к. объясняется возникающим в точках их контакта внутренним межчастичным трением, которое связанно с шероховатостью поверхности твердых частиц. В связных грунтах смещения частиц, кроме трения, оказывают силы внутреннего сцепления, обусловлены рядом факторов:

— наличием жестких кристаллизационных и цементационных структурных связей (природных цементов — коллоидных гелей и солей, как растворимых, так и не растворимых в воде) в точках контакта твердых частиц и по поверхностям оболочек связанной воды;

— наличием вязкопластических водно-коллоидных структурных связей, вызванных электро-молекулярными силами взаимодействия между твердыми частицами, с одной стороны, и пленками связанной воды, и коллоидными оболочками, прочно связанными с твердыми частицами — с другой;

— капиллярным давлением в зоне капиллярного увлажнения;

— взаимным заклиниванием и зацепленем частиц и тому подобное.

Вместе с тем, процесс деформирования грунта при сдвиге является очень сложным, и разграничивать сопротивление грунтов оползня на внутреннее трение и сцепление имеет в значительной степени условный характер. Так, невозможно выделить в чистом виде элементы, связанные с преодолением сил цементации структурных агрегатов, молекулярной связности, сопротивления деформированию водных пленок, взаимного заклинивания и зацепления частиц и т.д.

Количественные показатели сопротивления сдвигу — это основные характеристики прочности грунта. Они не постоянны и зависят от многих взаимосвязанных факторов: крупности и формы частиц грунта, его минералогического состава, степени водонасыщения и плотности строения, скорости приложения и продолжительности действия нагрузки и тому подобное. Правильный выбор показателей сопротивления сдвигу имеет важное значение для практики, ведь он вызывает точность расчетов большого перечня инженерных задач — предельного давления на грунт основания, устойчивости грунтовых массивов, давления грунтов на ограждающие сооружения и др.

В зависимости от физических свойств грунтов, обусловливающие их напряженно-деформированное состояние под зданием или сооружением, прочностные характеристики можно определять по результатам испытания грунтов методами консолидированного или неконсолидированного смещения.

Опытное определение показателей сопротивления грунтов сдвигу можно выполнять различными методами: по результатам прямого плоскостного сдвига, одноосного и трехосной сжатия, сдвига по цилиндрических поверхностях и др. Наиболее распространенными и простыми являются испытания при прямом плоскостном сдвиге.

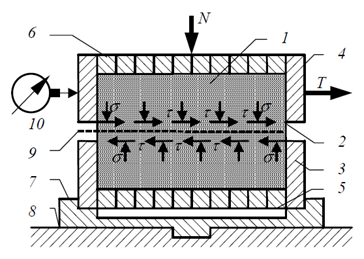
Цилиндрический образец грунта 1 после предварительного уплотнения размещают в разрезном кольце (гильзе) 2 оползневого прибора так, чтобы одна его половина оставалась неподвижной, а вторая могла перемещаться горизонтально под действием приложенной к ней оползневой нагрузки T, причем должна быть обеспечена возможность увеличения или уменьшения объема грунта при сдвиге.

К образцу прикладывают нормальную к поверхности сдвига 9 сжимающую нагрузку N. После полной стабилизации деформаций от ее действия, половинки гильзы раздвигают до образования небольшого зазора для устранения трения между ними.

Касательное к поверхности смещения нагрузки T прикладывают к верхней обойме оползневого прибора 4 ступенями до тех пор, пока не произойдет сдвиг и скольжение одной части грунта по второй. Одновременно с приложением оползневой нагрузки выполняют измерения горизонтальных деформаций грунта Δl индикатором 10. Происходит свободный отвод воды, которая выжимается из пор грунта при его сжатии, что осуществляется через фильтры 5 и 6. Сдвигающие силы T_i, отнесенные к площади поперечного сечения образца A в плоскости сдвига, дают касательные сдвигающие напряжения t_i, а силы N_i, отнесены к той же самой площади, дают нормальные плоскости сдвига сжимающие напряжения в образце s_i:

Выполняют смещение нескольких (не менее трех) образцов, обжимаемых различными вертикальными нормальными напряжениямиσ₁ … σ₃, которые в течение одного испытания оставляют неизменными, и определяют соответствующие им значения предельных касательных напряжений (предельных сопротивлений смещения)t_u,1… t_u,3.

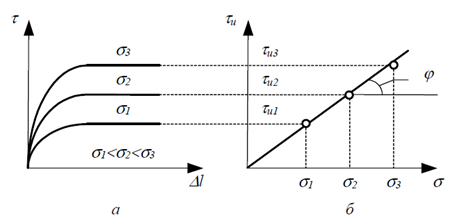
Результаты исследования сопротивления грунта сдвигу оформляют в виде графиков зависимостей горизонтальных деформаций грунта Δl_i от касательных напряжений t_i (2, а) и предельных сопротивлений смещения t_u,i от вертикальных нормальных сжимающих напряжений s_i (2, б).

Рисунок 2 — Графики сопротивлений смещению сыпучего грунта при различных вертикальных нормальных сжимающих напряжениях:а — горизонтальных перемещений Δl; б — предельных сопротивлений смещенииt_u

Как показывают многочисленные результаты исследований, для сыпучих грунтов (сухие пески и крупнообломочные грунты) в пределах обычных изменений вертикальных нормальных давлений, в большинстве случаев имеет место (от 0,05 до 0,5 … 0,7 МПа), зависимость между предельными опорами сдвига t_{u, i} и вертикальными нормальными сжимающими напряжениями s_i можно принять линейной из начала координат (рис. 2, б) в виде

где tgφ — коэффициент внутреннего трения, характеризующий трением между частицами; φ — угол наклона прямой к горизонтальной оси нормальных сжимающих напряжений, который называют углом внутреннего трения.

Эта зависимость установлена ​​еще в 1773 г.. Французским ученым Ш. Кулоном. Она выражает закон сопротивления сыпучих (несвязных) грунтов смещению, формулируется следующим образом: предельное сопротивление сыпучих грунтов сдвигу прямо пропорционально внешнему нормальному к плоскости сдвига давлению. Этот закон в механике грунтов называется закона Кулона для сыпучих грунтов.

В сопротивлении сдвига связных грунтов (глинистые грунты, сапропели и др.) решающую роль играет сцепление — составляющая, которая не зависит от величины вертикального нормального сжимающего напряжения.

Если по аналогичной методике в таком же приборе провести несколько (не менее трех) испытаний на сдвиг одного и того же связного грунта, подвергая образцы действию различных вертикальных нормальных сжимающих напряжений σ_i, то в общем случае можно получить криволинейную зависимость предельных сопротивлений грунта сдвигу (рис. 3).

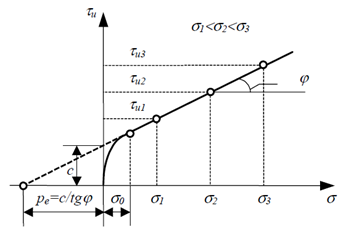
Рисунок 3 — График предельных сопротивлений смещения связного грунта при различных вертикальных нормальных сжимающих напряжениях.

Криволинейность зависимости наиболее ощутима при небольших значениях уплотнительных давлений (в пределах от 0 до σ₀=0,05 МПа). При нормальных сжимающих напряжениях в диапазоне σ_i = 0,05 … 0,5 МПа зависимость можно представить прямой линией, описываемой уравнением

где c — удельное сцепление грунта (величина отрезка, отсеченного прямой на вертикальной оси предельных сопротивлений смещения), МПа. Эта зависимость получила название закона Кулона для связных грунтов, формулируют так: предельное сопротивление связных грунтов сдвигу, при завершенной их консолидации, можно рассматривать как сумму сопротивления трения, прямо пропорционального внешнему нормальному к плоскости сдвига давлению, и сопротивления сцепления, независимого от этого давления.

Если линию зависимости t_{u, i}= ƒ(s_i) довести до пересечения с осью вертикальных нормальных к плоскости сдвига сжимающих напряжений, можно получить величину p_e, которую называют фиктивным давлением связности или условным эквивалентным давлением, создаваемым распределенными по объему грунта внутренними силами связности. Она может быть представлена как давление, необходимое для уплотнения, в условиях компрессионного испытания грунта, с влажностью на границе текучести (то есть такого, что практически не имеет сопротивления сдвигу) до состояния, в котором образец грунта находится при закладке в прибор для испытания на сдвиг.

Используя эквивалентное давление, параметр сцепления можно записать

Таким образом, угол внутреннего трения j_і и удельное сцепление c следует рассматривать как математические параметры прямолинейных диаграмм сопротивления грунтов сдвигу.

Источник

Предельное сопротивление сдвигу сыпучих и связных грунтов

Практику интересует в первую очередь максимально возможное сопротивление грунтов сдвигу, так называемое предельное сопротивление, т. е. когда наступает фаза такого напряженного состояния грунта, что возникают площадки скольжения (для которых максимальный угол отклонения равен углу трения) и нарушается сплошность грунта.

Сыпучие и связные грунты имеют свои особенности при изучении их предельного сопротивления сдвигу. Сыпучие грунты, как правило (исключение составляют лишь слюдистые пески), при увеличении или уменьшении внешнего давления незначительно изменяют свою плотность, и практически при давлениях от 1 до 4 кг/см2 этими изменениями можно пренебречь. Однако природная плотность песков или резкое изменение ее, например, при вибрировании уже существенно влияет и на сопротивление песков сдвигу.

После приложения вертикальной нагрузки и затухания деформаций от этой нагрузки образец подвергают в специальном односрезном приборе с зубчатыми штампом и поддоном действию постепенно возрастающей горизонтальной нагрузки до некоторой максимальной ее величины, при которой возникают беспрерывные скольжения (сдвиги) грунта по грунту. По полученному значению сдвигающей силы, которая вызывает незатухающие скольжения грунта, определяют величину сдвигающего напряжения как частное от деления сдвигающей силы на площадь среза. Таким образом, опытами определяется максимальное сопротивление грунта сдвигу, сверх которого грунт уже не может сопротивляться сдвигающей нагрузке, так как возникает беспрерывное скольжение одной части грунта по другой. По результатам нескольких срезов при различных внешних уплотняющих давлениях строится диаграмма зависимости между сжимающими напряжениями и сдвигающими.

Как показывают результаты многочисленных испытаний для сыпучих грунтов, диаграмма сопротивления сдвигу представляет собой строго прямую, исходящую из начала координат и отклоненную под углом к оси давлений. Так как сопротивление сыпучих грунтов сдвигу есть сопротивление их трению, то угол носит название угла внутреннего трения сыпучего грунта, и коэффициента внутреннего трения.

Зависимость установлена еще Кулоном в 1773 г.1 и может быть сформулирована следующим образом: сопротивление сыпучих грунтов сдвигу есть сопротивление трению, прямо пропорциональное нормальному давлению. Это и есть так называемый закон Кулона (третий закон механики грунтов) для сыпучих грунтов.

Связные грунты (глины, суглинки и супеси) отличаются от сыпучих грунтов тем, что частицы их связаны между собой адсорбированными пленками воды, коагулированными коллоидами и цементирующими веществами, вследствие чего даже при весьма малых деформациях сдвига грунт обладает известной прочностью, обусловленной силами сцепления.

Если общее сопротивление сыпучих грунтов сдвигу зависит от плотности упаковки их частиц, то сопротивление дисперсных связных грунтов сдвигу еще в большей степени зависит от их плотности и непосредственно связанной с ней влажности.

Так как в глинах влажность и давление связаны однозначной зависимостью, то при испытании глинистых и вообще всех дисперсных связных грунтов следует обращать особое внимание на то, чтобы все образцы испытываемого грунта имели практически одну и ту же влажность или плотность. Как было показано выше, это достигается путем испытания нескольких образцов грунта, предварительно уплотненных до наибольшего давления, а затем разгруженных до меньших значений давлений, при которых и определяется предельное сопротивление сдвигу.

Основными видами испытаний на сдвиг являются испытание по открытой системе (консолидированно-дренированное) и быстрое испытание по закрытой системе (неконсолидированно-недренированное). При испытании по открытой системе образцы грунта после разгрузки выдерживают до момента полного затухания их деформаций, т. е. когда давление полностью передастся на скелет грунта. Точно так же и сдвигающую нагрузку, прикладываемую возрастающими ступенями, выдерживают до практически полного затухания деформаций сдвига от каждой ступени в грунтах.

При исследовании связных грунтов испытывают несколько (не менее двух) образцов грунта на предельное сопротивление их прямому срезу. Как отмечалось ранее, при испытании плотных глин на приборах прямого среза необходимо учитывать фактическую поверхность среза, т. е. при небольших нагрузках вводить поправку на косой срез, пересчитывая напряжения по формулам, что может существенно сказаться на величине получаемых расчетных характеристик.

Результаты испытаний грунтов на сопротивление сдвигу изображают в виде диаграммы, откладывая по вертикальной оси максимальное (предельное) сопротивление сдвигу, а по горизонтальной — величину нормального сжимающего напряжения (эффективного давления).

Многочисленные испытания связных грунтов на сопротивление их прямому сдвигу показывают, что все экспериментальные точки при не очень больших давлениях (примерно меньших 7 кг/см2) весьма точно укладываются на прямую линию.

Закон Кулона для связных грунтов, может быть сформулирован следующим образом: предельное сопротивление связных грунтов сдвигу есть функция первой степени от нормального давления (сжимающего эффективного напряжения) и состоит из двух частей: первой, не зависящей от нормального давления, и второй, прямо пропорциональной нормальному давлению.

Величины являются математическими параметрами прямолинейной диаграммы сдвига, постоянными для данного физического состояния грунта (данной его плотности). Если связный грунт испытывает лишь весьма малые деформации сдвига, то его сопротивление будет зависеть почти исключительно от величины с, обусловленной действием всех видов сил связности, которое обычно называется сцеплением грунта, при больших же деформациях к сопротивлению сдвига будет прибавляться второе слагаемое, которое можно рассматривать как сопротивление грунта трению. Однако на практике бывает весьма трудно выделить часть сопротивления сдвигу, не зависящую от нормального давления (сцепление), и часть, ему прямо пропорциональную (трение), так как всякое изменение давлений сказывается не только на второй составляющей, но и на первой.

Если же испытывать глинистый грунт по закрытой системе (недренированное испытание) при различных давлениях, но без изменения содержания влаги (быстрый сдвиг), то обычно сопротивление сдвигу почти не будет зависеть от величины внешнего давления (сжимающего напряжения с), т. е. в этом случае сопротивление сдвигу определится силами сцепления грунта. Отметим, что если испытывать образцы глинистого грунта разной влажности по закрытой системе (недренированно-неконсолидированные испытания), то каждой плотности — влажности будут соответствовать свои значения параметров. Таким образом, сопротивление сдвигу связных деформаций сдвига будет определяться их сцеплением, а чисто сыпучих грунтов — только их трением. Во всех же остальных случаях не представляется возможным отделить «чистое сцепление» от «чистого трения», и расчетные характеристики сопротивления сдвигу грунтов необходимо рассматривать как математические параметры прямолинейной диаграммы сдвига связных грунтов.

Плотность сыпучих грунтов.

Естественная плотность сыпучих грунтов (песчаных и гравелистых различного состава, а также пылеватых песков) имеет первостепенное значение при оценке их свойств как оснований для сооружений, но определить ее в естественных условиях визуально (на глаз) не представляется возможным.

О плотности сыпучих грунтов судят или по величине их коэффициента пористости при сравнении с величиной коэффициента пористости тех же грунтов, но при более плотном и более рыхлом состоянии, или по результатам испытания грунтов в естественных условиях на пенетрацию (вдавливание).

Последний способ применяется для оценки как относительной плотности сыпучих, так и консистенции глинистых грунтов, а так же как особый метод опробования грунтов в природных условиях.

Для чистых сыпучих грунтов (преимущественно кварцевых) можно при оценке их плотности ограничиться определением лишь величины коэффициента пористости, соответствующего условиям естественного залегания.

Так, плотность песчаных грунтов по нормативным данным оценивается по величине коэффициента пористости (определяемого по образцам ненарушенной структуры или тарировочным зондом).

Конечно, для песков не кварцевых (например, слюдистых) эти данные непригодны. Поэтому для более общей характеристики плотности песчаных грунтов находят так называемый (Е мин) минимальный коэффициент пористости грунта в самом плотном состоянии (определяется для грунта, уплотненного до постоянного объема в металлической колбе путем вибрирования или многократного постукивания).

Поскольку определения Е макс. и Е мин. несколько условны, поэтому относительную плотность сыпучих грунтов, определяемую по, следует рассматривать лишь как качественную характеристику.

В зависимости от плотности природных песков (включая и пылеватые) по нормам рекомендуются различные величины расчетных сопротивлений, причем для рыхлых грунтов расчетное сопротивление вообще не нормируется, а рекомендуется определять его по результатам специальных исследований.

Для определения соотношения плотности отдельных пластов грунта в условиях их естественного залегания применяется зондирование (пенетрация), которое широко распространено, так как этот способ довольно дешевый.

Различают динамический метод зондирования, когда пенетрометр (обычно это конический наконечник, навинченный на буровую штангу) забивается в грунт на определенную глубину (около 30 см) стандартным грузом со стандартной высоты падения, и статический метод зондирования, когда конический пенетрометр на заданной отметке вдавливается в грунт, причем по динамометру, смонтированному на штанге, замеряется максимальное давление. Изменение давления при пенетрации по глубине скважины дает характеристику относительно плотности залегания грунтов. Следует указать, что в настоящее время больше применяется статическое зондирование по сравнению с динамическим, и уже предпринимаются попытки связать показатели статического зондирования с количественными характеристиками механических свойств грунтов.

Коэффициент водонасыщенности.

В условиях естественного залегания грунты обладают той или иной влажностью. В природных условиях можно встретить как воздушно-сухие грунты (например, пески выше уровня грунтовых вод), так и грунты, все поры которых заполнены водой.

Наличие в грунте воды влияет на пористость, а следовательно и на плотность залегания грунтов. Особое значение приобретает содержание воды в глинах. В зависимости от влажности глину можно рассматривать как вязкое, пластичное или твердое тело.

Определим вспомогательную в механике грунтов величину полную влагоемкость грунта, т. е. влажность, теоретически соответствующую полному заполнению пор водой. При полном заполнении пор водой вес содержащейся воды в грунте будет равен объему пор, умноженному на удельный вес воды, а вес сухого грунта — соответственно объему твердых частиц, умноженному на удельный вес грунта.

При полном заполнении пор грунта водой коэффициент пористости грунта, все поры которого заполнены водой, численно равен произведению весовой влажности грунта на его удельный вес.

Коэффициентом водонасыщенности называется отношение природной влажности грунта к его полной влагоемкости. Коэффициент водонасыщенности, или степень насыщения грунта водой также равняется отношению объема воды содержащейся в грунте, к объему его пор.

Для грунтов с жестким скелетом (пески, пылеватые грунты и пр.), имеющих мало изменяющуюся пористость, коэффициент водонасыщенности в известной мере характеризует свойства грунтов как оснований для сооружений. Для глинистых же грунтов в большинстве случаев коэффициент водонасыщенности будет близок к единице и для них более существенное значение имеют общее содержание воды и обусловленная им степень связанности. По нормам и техническим условиям проектирования естественных оснований песчаные грунты, а также лессовые глинистые в ависимости от степени насыщения их водой разделяют на:

Источник