объясните что такое функция
Что такое Функция?
7 класс, 11 класс, ЕГЭ/ОГЭ
Понятие функции
Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.
1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.
Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.
Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.
2. Функция — это определенное действие над переменной.
Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.
В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:
В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.
3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.
Например, в функции у = 2х каждому действительному числу х ставит в соответствие число в два раза большее, чем х.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида
область определения выглядит так:
И записать это можно так: D (y): х ≠ 0.
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.
В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.
Значение слова «функция»
1. Явление, зависящее от другого и изменяющееся по мере изменения другого явления. Литература в целом мире признается как одна из функций общественного бытия. Салтыков-Щедрин, Признаки времени.
2. Мат. Переменная величина, меняющаяся в зависимости от изменения другой величины (аргумента). Тригонометрические функции. □ [Володя], бойко постукивая мелом о черную доску, толкует о функциях, синусах, координатах и т. п. Л. Толстой, Отрочество.
3. Биол. Работа, производимая органом, организмом, как проявление его жизнедеятельности. Вот вам азбука биологии: если какой-нибудь орган продолжительное время не упражнять, то он утрачивает способность отправлять свои функции. Федин, Города и годы. [Котельников:] Проблема сводится к восстановлению жизненных функций организма, пораженного тем или иным ядом. Лавренев, Мы будем жить!
4. перен. Обязанность, круг деятельности. — [Развалихин] утром сказал, что пойдет в школу проводить обществоведение вместо тебя. «Это, говорит, моя прямая функция, а не Корчагина». Н. Островский, Как закалялась сталь.
5. Значение, назначение, роль. Функция творительного падежа. Функции денег.
[От лат. functio — исполнение]
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
Функция (философия) — обязанность, круг деятельности.
Функция (работа) — работа, производимая органом, организмом, прибором; роль, значение чего-либо; назначение чего-либо.
Функция (литературоведение) — назначение персонажа в литературном произведении.
Социальная функция — использование того или иного механизма социальных взаимодействий для достижения определённой цели или реализации определённых ценностей.
Функция (математика) — закон зависимости одной величины от другой.
Функция (программирование) — вид подпрограммы в информатике.
Функциональная зависимость (программирование) — в теории реляционных баз данных.
ФУ’НКЦИЯ, и, ж. [латин. functio — выполнение работы]. 1. Явление, зависящее от другого и изменяющееся по мере изменения этого другого явления (книжн.). 2. Переменная величина, меняющаяся в зависимости от изменения другой величины (мат.). Величина давления газа есть функция величины его объема. 3. Работа, производимая органом, организмом (биол., физиол.). Отделение слюны является основной функцией слюнной железы. 4. перен. Обязанность, круг деятельности чего-н., подлежащая исполнению работа (книжн.). Служебные функции. Исполнять свою функцию в обществе. Функции государственного управления. 5. Значение, назначение, роль (книжн.). Ф. математического знака. Ф. родительного падежа.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
фу́нкция
1. перен. книжн. обязанность, круг деятельности чего-либо, подлежащая исполнению работа ◆ Служебные функции. ◆ Исполнять свою функцию в обществе. ◆ Функции государственного управления.
2. книжн. значение, назначение, роль ◆ Функция математического знака. ◆ Функция родительного падежа.
3. матем. переменная величина, меняющаяся в зависимости от изменения другой величины, а также закон, определяющий свойства такого изменения ◆ Величина давления газа есть функция величины его объёма.
4. книжн. явление, зависящее от другого и изменяющееся по мере изменения этого другого явления
5. биол. физиол. работа, производимая органом, организмом. ◆ Выделение слюны является основной функцией слюнной железы.
7. комп. в программировании — фрагмент программного кода (подпрограмма), к которому можно обратиться из другого места программы.
Что такое функция?
Это слово используется очень часто. И в научном диспуте и обычной болтовне… Но кто и из нас точно знает, о чем идет речь? Что такое функция?
Простое объяснение функции — это зависимость, связь или действие. Все зависит от контекста, но к концу этой статьи все станет ясно и понятно (и самому автору тоже).
История функции
Само слово “функция” — латинского происхождения. С латыни оно переводится как “выполнение” или “совершение”, что в принципе одно и то же — действие. Функционировать, и сейчас означает выполнять какое-то действие.
Что такое функция в математике
В математике функция означает — «зависимость». Это самое простое и короткое объяснение. Но для тех, кому еще не стало все понятно…
Больше всего трудностей с пониманием как обычно нам дарит как раз математика. Термин функция в математике появился, лишь в 17-м веке. Хотя само явление было известно гораздо раньше именно в переписке двух математиков Бернули и Лейбница это слово было употреблено в значении очень близком к современному.
Функция существовала в математике и до этого, просто общепринятого термина и его определение не было. Например, не менее известные, Пьер Ферма (автор теоремы своего имени), Рене Декарт и даже Ньютон, отлично понимали предмет, но не пользовались термином.
Первое определение функции в математике дал Леонард Эйлер в 1751 году. До Эйлера функцию объясняли как:
Некоторое сопоставление постоянных и переменных
Эйлер же выразился намного более определенно:
Эйлер считал, что функция — это соответствие между парами чисел.
Когда некоторые количества зависят от других таким образом, что при изменении последних и сами они подвергаются изменению, то первые называются функциями вторых…
Зависимость одного множества чисел от другого и есть функция. В то время, когда знаменитый математик написал эти слова, он был участником так называемого спора о струне.
Итак, зависимость (или связь или соответствие) одного множества от другого.
Эта зависимость обозначается буквой ƒ
Здесь x это аргумент функции, или независимая переменная, а y — зависимая переменная или “функция икс”.
Это можно прочитать как “каждому значению игрек соответствует определенное (а определяется оно законом f(x)) значение икс” или “игрек зависит от икс по некоторому закону.”
То есть когда какие либо два набора (множества) чисел или объектов связаны между собой по какому-то закону, мы имеем дело с функцией. Икс и игрек это просто буквы которые принято использовать сами по себе они ничего не значат, можно написать любые другие.
Например: Давление воды, это функция глубины.
Чем глубже, тем выше будет давление. Пословица “Чем дальше в лес, тем больше дров” — тоже функция (количества дров от расстояния), а “Как с гуся вода” — уже нет. Потому, что гусь с водой никаким законом не связан.
Запись y=f(x) говорит о том, что между х и у есть связь, но непонятно какая. Она может быть у=х (каждому игреку свой икс), а может и у=2х (каждому игреку соответствует икс умноженный на два). Зависимость может быть любой, но она должна быть.
Функция в физике
Функция — может быть, например, величиной изменяющейся с течением времени (или не времени, а чего-то другого, просто время более понятно).
Например, скорость это функция изменения расстояния от времени. Если расстояние пройденное за определенное время разделить на это время получим — скорость.
v=s/t x=f(t) функция изменения координаты по времени. Можно сказать ”зависимость изменения координат от времени.”
Физика, как наука “о природе” помогает лучше понять математику. Тут все можно объяснить простыми словами, даже «функцию».
Давайте представим самую обычную ситуацию. Человек куда-то идет. За первый час он прошел 5 километров, за второй еще 5, потом еще…Через 3 часа он устал, и начал идти медленнее — 4 км…. В конечном итоге (через 5 часов прогулки, и вовсе остановился, чтобы отдохнуть.
Мы гуляли 5 часов и протопали 5+5+5+4+3=22 километра (воображаемый человек не курит и гуляет в удобной обуви). Зависит ли пройденное расстояние от времени? Конечно да, чем дальше гуляем, тем дальше окажемся от дома. Расстояние зависит от времени — это функция. В столбике выше у нас ее табличное выражение.
Причем в первые три часа функция линейная, а дальше — уже нет. Почему? В реальном мире, из-за усталости скорость уменьшилась. А в “мире науки”. Если взять изобретение господина Декарта и нарисовать то, что у нас в таблице.
Получится график функции или ее графическое изображение. На графике видно, что первые 3 часа наш пешеход шел с одинаковой скоростью, линия прямая (зеленого цвета). Он устал и начал идти медленнее, и с каждым шагом все медленнее и медленнее (оранжевая кривая линия). Если бы линия была прямой все время, мы бы преодолели расстояние в 25 км. Но это не так. Делим расстояние 15 км на 3 часа и получаем скорость 5 км/ч делим 4 на 1 час и 3 тоже на 1 и получаем скорости 4 км/ч и 3 км/ч.
Но прелесть зависимости в том, что если мы захотим узнать, какая скорость была через 4 часа и 30 минут, достаточно провести линию снизу вверх до пересечения с графиком (синяя точка) и справа налево до оси на которой находится расстояние и поделить одно на другое (расстояние на время). Можно даже узнать, что будет если не остановится и не отдыхать. Продлеваем график еще на один час и вуаля:
Ну это на графике, а в самой первой таблице нет времени 4:30 и нет ничего после 6-ого часа.
Нет и не нужно. Функция — это зависимость и выразить ее можно еще одним способом — аналитическим. Получится формула.
Здесь t — это аргумент функции, такой же, как и “икс” в абзаце о математике. А “икс” обозначения координаты которая меняется в зависимости от времени t.
Зная по какому закону время зависит от расстояния, можно рассчитать скорость в любой момент времени.
В нашем примере закон у=5х или s=5t, но только на участке от нуля до трех, дальше зависимость нелинейная и отражается кривой линией. Но
С другой стороны, есть значение слова “действие” (если еще не забыли). Кто с кем и что делает? В нашем примере расстояние меняется со временем. Это то же самое, что и “время изменяет расстояние”? В принципе, да вполне логично.
Математики вообще могут сказать что, “оператор f действует из множества х в множество y”.
Функция — роль и предназначение
Функция молотка — забивание гвоздей. А Центрального банка (не единственная) — выдача кредитов банкам помельче.
Вот мы и вернулись к первоначальному значению латинского слова “выполнять”. Молоток (выполняет работу) по забиванию гвоздей. Банк (выполняет работу) по выдаче кредитов. В обоих случаях есть и связь одного с другим и какое-то действие оправдывающее существование и молотка и банка.
В программировании функция — это код выполняющий определенную задачу. Подпрограмма которую можно “вызывать” (обычно много раз) для выполнения некой задачи. Вот пример из php (языка, который используется на этом сайте):
Даже не будучи программистом становится понятно, что функция по имени «sum» суммирует 2 переменные.
Итак функция, это зависимость, или работа, или предназначение… Зависит от контекста, но всегда есть минимум две сущности (может быть и больше) связанные каким-то правилом или законом, которые действуют одна на другую. Что-то с чем-то связано, кто-то на что-то оказывает влияние. Такая одновременно и простое и сложное, почти философское понятие, но встречается нам каждый день.
Что такое функция в математике
Понятие функции в математике появилось не просто так. Давайте разберемся, зачем придумали функцию и как с ней можно работать.
| Сколько времени двигается автомобиль | Сколько км проедет автомобиль |
|---|---|
| 1 час | 60 км |
| 2 часа | 120 км |
| 3 часа | 180 км |
Если внимательно изучить таблицу станет очевидно, что между временем автомобиля в пути и пройденным расстоянием есть четкая зависимость.
Обозначим за « x » время автомобиля в пути.
Обозначим за « y » расстояние, пройденное автомобилем.
Запишем зависимость « y » (расстояния) от « x » (времени в пути автомобиля).
Давайте убедимся, что мы правильно записали зависимость пройденного расстояния от времени в пути.
Теперь вместо « y » запишем обозначение « y(x) ». Такая запись означает, что « y » зависит от « x ».
Окончательная запись нашей функции, которая показывает зависимость пройденного автомобилем расстояния от времени в пути, выглядит следующим образом:
Функцией называют зависимость « y » от « x ».
Запись функции в виде « y(x) = 60x » называют формульным способом задания функции.
Конечно, нужно понимать, что функция « y(x) = 60x » — это не единственная в мире функция. В математике бесконечное множество самых разнообразных функций.
Примеры других функций:
Единственное, что объединяет все функции, это то, что они показывают зависимость значения функция (« y ») от её аргумента (« x »).
Способы задания функции
Задание функции формулой
Через формульный способ задания функции всегда можно сразу по конкретному значению аргумента « x » найти значение функции « y ».
Например, рассмотрим функцию, заданную формульным способом.
Запишем расчет следующим образом.
Табличный способ задания функции
С табличным способом задания функции мы уже встречались, когда расписывали таблицу для функции, которая описывает движение автомобиля « y(x) = 60x ».
Любую функцию можно записать с помощью таблицы. Для этого достаточно найти несколько значений « y » для произвольно выбранных значений « x ».
Будьте внимательны, когда подставляете значение « x » в функцию,
у которой перед « x » есть минус.
Нельзя терять знак минуса, который стоит перед « x ».
При подстановки отрицательного числа в функцию вместо « x » обязательно заключайте отрицательное число в скобки. Не забывайте использовать правило знаков.
Подставим в функцию « y(x) = −x + 4 » вместо « x » отрицательное число « −1 ».
Неправильно
Правильно
Запишем полученные результаты в таблицу. Таким образом мы получили табличный способ задания функции « y(x) = −x + 4 ».
| x | y |
|---|---|
| −1 | 5 |
| 0 | 4 |
| 1 | 3 |
Графический способ задания функции
Теперь давайте разберемся, что называют графиком функции и как его построить.
Прежде чем перейти к изучению графического способа задания функции обязательно вспомните, что называют прямоугольной системой координат.
Рассмотрим функцию « y(x) = −2x + 1 ».
Результаты запишем в таблицу.
| x | Расчет |
|---|---|
| −1 | y(−1) = −2 · (−1) + 1 = 2 + 1 = 3 |
| 0 | y(0) = −2 · 0 + 1 = 0 + 1 = 1 |
| 1 | y(1) = −2 · 1 + 1 = −2 + 1 = −1 |
Назовем каждую полученную точку и запишем их координаты в новую таблицу.
| Имя точки | x | y |
|---|---|---|
| (·) A | −1 | 3 |
| (·) B | 0 | 1 |
| (·) C | 1 | −1 |
Соединим отмеченные точки прямой. Проведенная прямая будет графиком функции « y(x) = −2x + 1 ».
График функции — это объединение всех точек, координаты которых мы можем найти, подставляя в функцию произвольные числовые значения вместо « x ».
Другими словами можно сказать, что под графиком функции мы понимаем множество всех точек, координаты которых мы можем найти, подставляя в функцию любые числовые значения вместо « x ».
Полученный график функции « y(x) = −2x + 1 » это бесконечное множество точек, которые лежат на одной прямой.
При многократном увеличении графика функции мы увидим, что в самом деле вся прямая состоит из рядом стоящих точек.
Точки располагаются максимально близко к друг другу, поэтому по расчетам получается, что графиком функции будет являться прямая.
Что такое функция
Понятие функции – одно из основных в математике.
На уроках математики вы часто слышите это слово. Вы строите графики функций, занимаетесь исследованием функции, находите наибольшее или наименьшее значение функции. Но для понимания всех этих действий давайте определим, что такое функция.
Определение функции можно дать несколькими способами. Все они будут дополнять друг друга.
1. Функция – это зависимость одной переменной величины от другой. Другими словами, взаимосвязь между величинами.
Чем больше глубина, тем больше давление жидкости. Можно сказать, что давление жидкости является функцией от глубины, на которой его измеряют.
2. Можно дать и другое определение.
Функция – это определенное действие над переменной.
Итак, функция – это действие над переменной. В этом значении слово «функция» применяется и в областях, далеких от математики. Например, можно говорить о функциях мобильного телефона, о функциях головного мозга или функциях депутата. Во всех этих случаях речь идет именно о совершаемых действиях.
3. Дадим еще одно определение функции – то, что чаще всего встречается в учебниках.
Функция – это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один и только один элемент второго множества.
Но зачем здесь такое длинное уточнение: «каждому элементу первого множества соответствует один и только один элемент второго»? Оказывается, что соответствия между множествами тоже бывают разные.
Могут быть и другие типы соответствий между множествами. Возьмем для примера компанию друзей и месяцы, в которые они родились:
Каждый человек родился в какой-то определенный месяц. Но данное соответствие не является взаимно-однозначным. Например, в июне родились Сергей и Олег.
А каким должно быть соответствие между двумя множествами, чтобы оно не являлось функцией? Очень просто! Возьмем ту же компанию друзей и их хобби:
Мы видим, что в первом множестве есть элементы, которым соответствует два или три элемента из второго множества.
Очень сложно было бы описать такое соответствие математически, не правда ли?
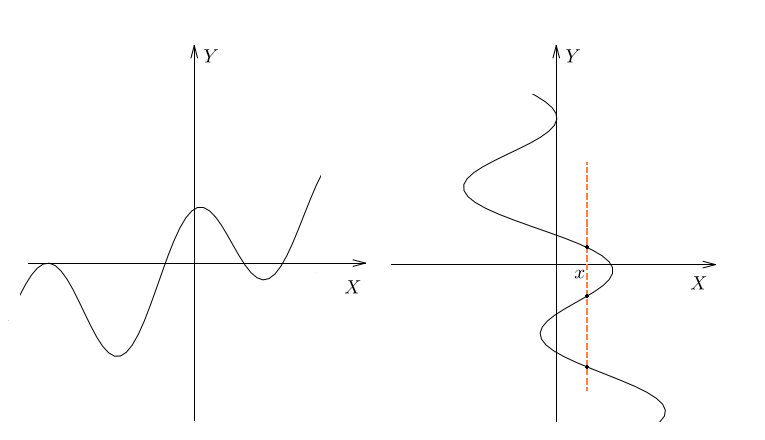
Вот другой пример. На рисунках изображены кривые. Как вы думаете, какая из них является графиком функции, а какая – нет?
Ты нашел то, что искал? Поделись с друзьями!
Перечислим способы задания функции.
Это примеры функций, заданных формулами.
К тому же не всегда легко вывести точную формулу функции. Например, курс доллара (то есть зависимость стоимости доллара от времени) можно показать только на графике.