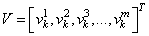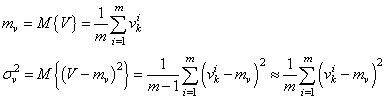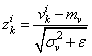обучение по батчам нужно потому что несколько вариантов ответов

Эпоха, батч, итерация — в чем различия?

Вам должны быть знакомы моменты, когда вы смотрите на код и удивляетесь: “Почему я использую в коде эти три параметра, в чем отличие между ними?”. И это неспроста, так как параметры выглядят очень похожими.

Чтобы выяснить разницу между этими параметрами, требуется понимание простых понятий, таких как градиентный спуск.

Градиентный спуск

Это ни что иное, как алгоритм итеративной оптимизации, используемый в машинном обучении для получения более точного результата (то есть поиск минимума кривой или многомерной поверхности).

Градиент показывает скорость убывания или возрастания функции.

Спуск говорит о том, что мы имеем дело с убыванием.

Алгоритм итеративный, процедура проводится несколько раз, чтобы добиться оптимального результата. При правильной реализации алгоритма, на каждом шаге результат получается лучше. Таким образом, итеративный характер градиентного спуска помогает плохо обученной модели оптимально подстроиться под данные.

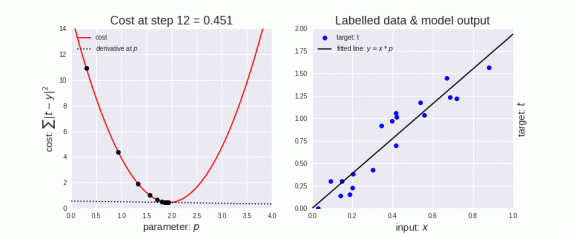
У градиентного спуска есть параметр, называемый скоростью обучения. На левой верхней картинке видно, что в самом начале шаги больше, то есть скорость обучения выше, а по мере приближения точек к краю кривой скорость обучения становится меньше благодаря уменьшению размера шагов. Кроме того, значение функции потерь (Cost function) уменьшается, или просто говорят, что потери уменьшаются. Часто люди называют функцию потерь Loss-функцией или просто «Лосс». Важно, что если Cost/Loss функция уменьшается, то это хорошо.

Как происходит обучение сети

Исследователи работают с гиганскими объемами данных, которые требуют соответствующих затрат ресурсов и времени. Чтобы эффективно работать с большими объемами данных, требуется использовать параметры (epoch, batch size, итерации), так как зачастую нет возможности загрузить сразу все данные в обработку.

Для преодоления этой проблемы, данные делят на части меньшего размера, загружают их по очереди и обновляют веса нейросети в конце каждого шага, подстраивая их под данные.

Epochs

Произошла одна эпоха (epoch) — весь датасет прошел через нейронную сеть в прямом и обратном направлении только один раз.

Так как одна epoch слишком велика для компьютера, датасет делят на маленькие партии (batches).

Почему мы используем более одной эпохи

Вначале не понятно, почему недостаточно одного полного прохода датасета через нейронную сеть, и почему необходимо пускать полный датасет по сети несколько раз.

Нужно помнить, что мы используем ограниченный датасет, чтобы оптимизировать обучение и подстроить кривую под данные. Делается это с помощью градиентного спуска — итеративного процесса. Поэтому обновления весов после одного прохождения недостаточно.

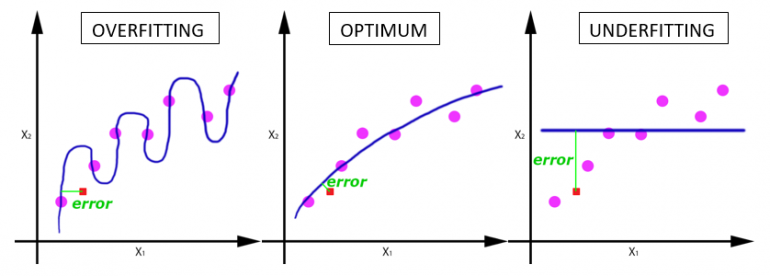
Одна эпоха приводит к недообучению, а избыток эпох — к переобучению:

С увеличением числа эпох, веса нейронной сети изменяются все большее количество раз. Кривая с каждый разом лучше подстраивается под данные, переходя последовательно из плохо обученного состояния (последний график) в оптимальное (центральный график). Если вовремя не остановиться, то может произойти переобучение (первый график) — когда кривая очень точно подстроилась под точки, а обобщающая способность исчезла.

Какое количество эпох правильное?

На этот вопрос нет единственного точного ответа. Для различных датасетов оптимальное количество эпох будет отличаться. Но ясно, что количество эпох связано с разнообразием в данных. Например, в вашем датасете присутствуют только черные котики? Или это более разнообразный датасет?

Batch Size

Общее число тренировочных объектов, представленных в одном батче.

Отметим: Размер батча и число батчей — два разных параметра.

Что такое батч?

Нельзя пропустить через нейронную сеть разом весь датасет. Поэтому делим данные на пакеты, сеты или партии, так же, как большая статья делится на много разделов — введение, градиентный спуск, эпохи, Batch size и итерации. Такое разбиение позволяет легче прочитать и понять статью.

Итерации

Итерации — число батчей, необходимых для завершения одной эпохи.

Отметим: Число батчей равно числу итераций для одной эпохи.

Например, собираемся использовать 2000 тренировочных объектов.

Можно разделить полный датасет из 2000 объектов на батчи размером 500 объектов. Таким образом, для завершения одной эпохи потребуется 4 итерации.

Источник

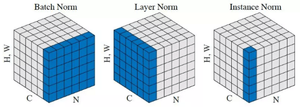
Batch Normalization (батч-нормализация) что это такое?

Вам что-нибудь говорит термин внутренний ковариационный сдвиг:

internal covariance shift

Звучит очень умно, не так ли? И не удивительно. Это понятие в 2015-м году ввели два сотрудника корпорации Google:

Sergey Ioffe и Christian Szegedy (Иоффе и Сегеди)

решая проблему ускорения процесса обучения НС. И мы сейчас посмотрим, что же они предложили, как это работает и, наконец, что же это за ковариационный сдвиг. Как раз с последнего я и начну.

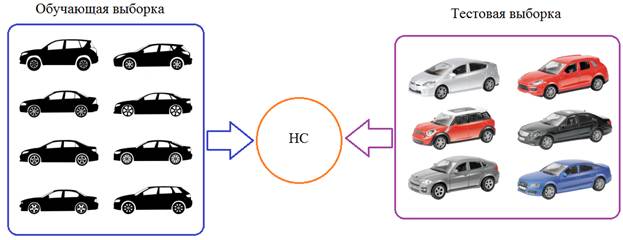
Давайте предположим, что мы обучаем НС распознавать машины (неважно какие, главное чтобы сеть на выходе выдавала признак: машина или не машина). Но, при обучении мы используем автомобили только черного цвета. После этого, сеть переходит в режим эксплуатации и ей предъявляются машины уже разных цветов:

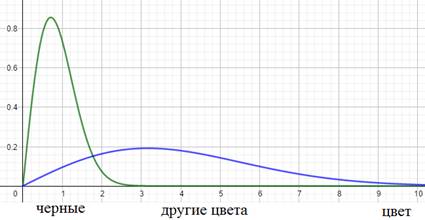
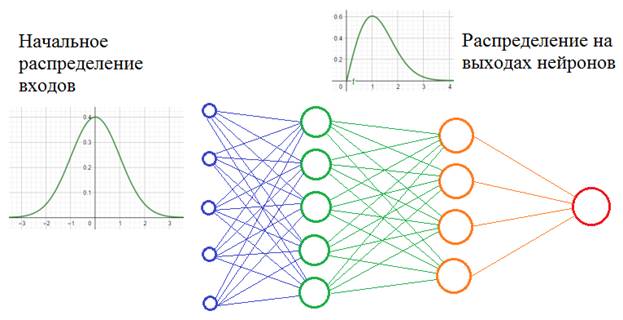
Как вы понимаете, это не лучшим образом скажется на качестве ее работы. Так вот, на языке математики этот эффект можно выразить так. Начальное распределение цветов (пусть это будут градации серого) обучающей выборки можно описать с помощью вот такой плотности распределения вероятностей (зеленый график):

А распределение всего множества цветов машин, встречающихся в тестовой выборке в виде синего графика. Как видите эти графики имеют различные МО и дисперсии. Эта разница статистических характеристик и приводит к ковариационному сдвигу. И теперь мы понимаем: если такой сдвиг имеет место быть, то это негативно сказывается на работе НС.

Но это пример внешнего ковариационного сдвига. Его легко исправить, поместив в обучающую выборку нужное количество машин с разными цветами. Есть еще внутренний ковариационный сдвиг – это когда статистическая картина меняется внутри сети от слоя к слою:

Само по себе такое изменение статистик не несет каких-либо проблем. Проблемы проявляются в процессе обучения, когда при изменении весов связей предыдущего слоя статистическое распределение выходных значений нейронов текущего слоя становится заметно другим. И этот измененный сигнал идет на вход следующего слоя. Это похоже на то, словно на вход скрытого слоя поступают то машины черного цвета, то машины красного цвета или какого другого. То есть, весовые коэффициенты в пределах мини-батча только адаптировались к черным автомобилям, как в следующем мини-батче им приходится адаптироваться к другому распределению – красным машинам и так постоянно. В ряде случаев это может существенно снижать скорость обучения и, кроме того, для адаптации в таких условиях приходится устанавливать малое значение шага сходимости, чтобы весовые коэффициенты имели возможность подстраиваться под разные статистические распределения.

Это описание проблемы, которую, как раз, и выявили сотрудники Гугла, изучая особенности обучения многослойных НС. Решение кажется здесь очевидным: если проблема в изменении статистических характеристик распределения на выходах нейронов, то давайте их стандартизировать, нормализовывать – приводить к единому виду. Именно это и делается при помощи предложенного алгоритма

Осталось выяснить: какие характеристики и как следует нормировать. Из теории вероятностей мы знаем, что самые значимые из них – первые две: МО и дисперсия. Так вот, в алгоритме batch normalization их приводят к значениям 0 и 1, то есть, формируют распределение с нулевым МО и единичной дисперсией. Чуть позже я подробнее поясню как это делается, а пока ответим на второй вопрос: для каких величин и в какой момент производится эта нормировка? Разработчики этого метода рекомендовали располагать нормировку для величин перед функцией активации:

Но сейчас уже имеются результаты исследований, которые показывают, что этот блок может давать хорошие результаты и после функции активации.

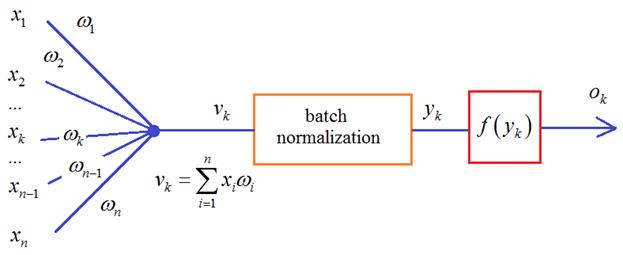
Что же из себя представляет batch normalization и где тут статистики? Давайте вспомним, что НС обучается пакетами наблюдений – батчами. И для каждого наблюдения из batch на входе каждого нейрона получается свое значение суммы:

Здесь m – это размер пакета, число наблюдений в батче. Так вот статистики вычисляются для величин V в пределах одного batch:

И, далее, чтобы вектор V имел нулевое среднее и единичную дисперсию, каждое значение преобразовывают по очевидной формуле:

здесь — небольшое положительное число, исключающее деление на ноль, если дисперсия будет близка к нулевым значениям. В итоге, вектор

будет иметь нулевое МО и почти единичную дисперсию. Но этого недостаточно. Если оставить как есть, то будут теряться естественные статистические характеристики наблюдений между батчами: небольшие изменения в средних значениях и дисперсиях, т.е. будет уменьшена репрезентативность выборки:

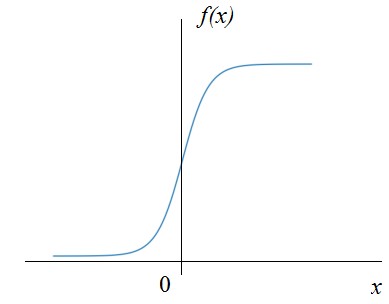
Кроме того, сигмоидальная функция активации вблизи нуля имеет практически линейную зависимость, а значит, простая нормировка значений x лишит НС ее нелинейного характера, что приведет к ухудшению ее работы:

Поэтому нормированные величины дополнительно масштабируются и смещаются в соответствии с формулой:

Параметры с начальными значениями 1 и 0 также подбираются в процессе обучения НС с помощью того же алгоритма градиентного спуска. То есть, у сети появляются дополнительные настраиваемые переменные, помимо весовых коэффициентов.

Но это лишь возможные эффекты – они могут и не проявиться или даже, наоборот, применение этого алгоритма ухудшит обучаемость НС. Рекомендация здесь такая:

Изначально строить нейронные сети без batch normalization (или dropout) и если наблюдается медленное обучение или эффект переобучения, то можно попробовать добавить batch normalization или dropout, но не оба вместе.

Реализация batch normalization в Keras

Давайте теперь посмотрим как можно реализовать данный алгоритм в пакете Keras. Для этого существует класс специального слоя, который так и называется:

Он применяется к выходам предыдущего слоя, после которого указан в модели НС, например:

Здесь нормализация применяется к выходам скрытого слоя, состоящего из 300 нейронов. Правда в такой простой НС нормализация, скорее, негативно сказывается на обучении. Этот метод обычно помогает при большом числе слоев, то есть, при deep learning.

Видео по теме

Нейронные сети: краткая история триумфа

Структура и принцип работы полносвязных нейронных сетей | #1 нейросети на Python

Ускорение обучения, начальные веса, стандартизация, подготовка выборки | #4 нейросети на Python

Функции активации, критерии качества работы НС | #6 нейросети на Python

Как нейронная сеть распознает цифры | #9 нейросети на Python

Оптимизаторы в Keras, формирование выборки валидации | #10 нейросети на Python

Batch Normalization (батч-нормализация) что это такое? | #12 нейросети на Python

Как работают сверточные нейронные сети | #13 нейросети на Python

Делаем сверточную нейронную сеть в Keras | #14 нейросети на Python

Примеры архитектур сверточных сетей VGG-16 и VGG-19 | #15 нейросети на Python

Теория стилизации изображений (Neural Style Transfer) | #16 нейросети на Python

Делаем перенос стилей изображений с помощью Keras и Tensorflow | #17 нейросети на Python

Как нейронная сеть раскрашивает изображения | #18 нейросети на Python

Введение в рекуррентные нейронные сети | #19 нейросети на Python

Как рекуррентная нейронная сеть прогнозирует символы | #20 нейросети на Python

Делаем прогноз слов рекуррентной сетью Embedding слой | #21 нейросети на Python

Как работают RNN. Глубокие рекуррентные нейросети | #22 нейросети на Python

Как делать сентимент-анализ рекуррентной LSTM сетью | #24 нейросети на Python

Рекуррентные блоки GRU. Пример их реализации в задаче сентимент-анализа | #25 нейросети на Python

Двунаправленные (bidirectional) рекуррентные нейронные сети | #26 нейросети на Python

Автоэнкодеры. Что это и как работают | #27 нейросети на Python

Вариационные автоэнкодеры (VAE). Что это такое? | #28 нейросети на Python

Делаем вариационный автоэнкодер (VAE) в Keras | #29 нейросети на Python

Расширенный вариационный автоэнкодер (CVAE) | #30 нейросети на Python

Что такое генеративно-состязательные сети (GAN) | #31 нейросети на Python

Делаем генеративно-состязательную сеть в Keras и Tensorflow | #32 нейросети на Python

© 2021 Частичное или полное копирование информации с данного сайта для распространения на других ресурсах, в том числе и бумажных, строго запрещено. Все тексты и изображения являются собственностью сайта

Источник

Batch-normalization

Содержание

Идея [ править ]

Пакет [ править ]

Также существует «золотая середина» между стохастическим градиентным спуском и пакетным градиентным спуском — когда просматривается только некоторое подмножество обучающей выборки фиксированного размера (англ. batch-size). В таком случае такие подмножества принято называть мини-пакетом (англ. mini-batch). Здесь и далее, мини-пакеты будем также называть пакетом.

Ковариантный сдвиг [ править ]

Пакетная нормализация уменьшает величину, на которую смещаются значения узлов в скрытых слоях (т.н. ковариантный сдвиг (англ. covariance shift)).

Ковариантный сдвиг — это ситуация, когда распределения значений признаков в обучающей и тестовой выборке имеют разные параметры (математическое ожидание, дисперсия и т.д.). Ковариантность в данном случае относится к значениям признаков.

Простой способ решить проблему ковариантного сдвига для входного слоя — это случайным образом перемешать данные перед созданием пакетов. Но для скрытых слоев нейронной сети такой метод не подходит, так как распределение входных данных для каждого узла скрытых слоев изменяется каждый раз, когда происходит обновление параметров в предыдущем слое. Эта проблема называется внутренним ковариантным сдвигом (англ. internal covariate shift). Для решения данной проблемы часто приходится использовать низкий темп обучения (англ. learning rate) и методы регуляризации при обучении модели. Другим способом устранения внутреннего ковариантного сдвига является метод пакетной нормализации.

Свойства пакетной нормализации [ править ]

Кроме того, использование пакетной нормализации обладает еще несколькими дополнительными полезными свойствами:

Описание метода [ править ]

Данные параметры настраиваются в процессе обучения вместе с остальными параметрами модели.

Тогда алгоритм пакетной нормализации можно представить так:

Обучение нейронных сетей с пакетной нормализацией [ править ]

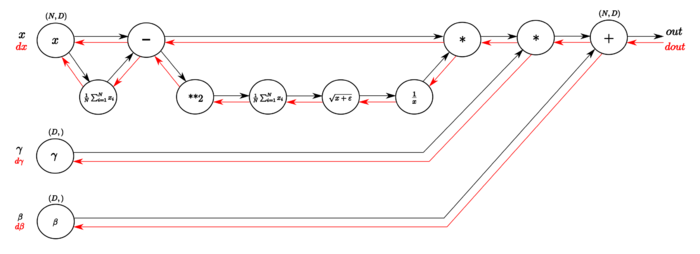
На Рисунке [math]2[/math] изображен граф вычислений слоя пакетной нормализации алгоритмом обратного распространения ошибки.

В обратном направлении вычисляются производные необходимых функций. В следующей таблице подробнее изображены шаги вычисления градиента функции потерь (иллюстрации из статьи, здесь [math]N=m[/math] и [math]D=d[/math] ):

Пакетная нормализация в свёрточных сетях [ править ]

Пакетная нормализация может быть применена к любой функции активации. Рассмотрим подробнее случай аффинного преобразования с некоторой нелинейной функцией:

где [math]BN[/math] применяется отдельно к каждой размерности [math]x=Wu[/math] с отдельной парой параметров [math]\gamma^<(k)>[/math] и [math]\beta^<(k)>[/math] для каждой размерности.

Индивидуальная нормализация [ править ]

Условная пакетная нормализация [ править ]

Описание метода [ править ]

Выбор параметров нормализации [ править ]

В применении к переносу стиля [ править ]

Добавление условности [ править ]

Такой подход имеет много преимуществ по сравнению с наивным:

Когда использовать условную нормализацию? [ править ]

Во-первых, на условную нормализацию стоит обратить внимание, если вы настраиваете много сетей, решающих похожие задачи. Возможно, в этом случае вы можете использовать одну сеть с условными параметрами нормализации, зависящими от конкретной задачи. Например, при переносе стилей вместо [math]S[/math] сетей вы настраиваете одну сеть с [math]S[/math] наборами параметров нормализации.

Во-вторых, если вы подозреваете, что информация о структуре входных векторов имеет значение для выхода. Например, имеет смысл «слить» лингвистическую информацию и характеристики изображения для задачи ответа на визуальные вопросы (англ. Visual Question Answering, VQA).

Однако во всех случаях надо помнить, что полученные алгоритмы для разных задач будут различаться лишь параметрами свёртки и сжатия. Иначе говоря, если ваши задачи нельзя выразить аффинной комбинацией параметров сети после нормализации, условная нормализация не поможет.

Пример [ править ]

Реализации [ править ]

Приведем пример [11] применения пакетной нормализации с использованием библиотеки TensorFlow на языке программирования Python [12] :

Модификации [ править ]

Существует несколько модификаций и вариаций метода пакетной нормализации:

Источник

Записная книжка

Компьютерное зрение, машинное обучение, нейронные сети и т.п.

Batch Normalization. Основы.

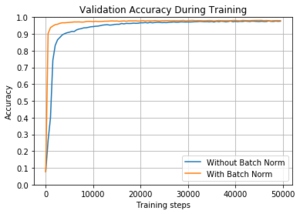
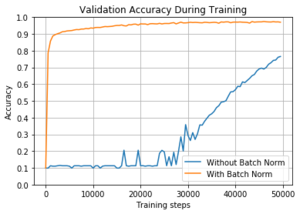
Главные наблюдаемые достоинства batch normalization это ускорение тренировки (в смысле уменьшения количества итераций для получения нужного качества) и некая допускаемая вольность в подборе параметров: и инициализации весов сети, и learning rate и других метапараметров обучения. Таким образом ценность batch Normalization для нейронных сетей сложно преувеличить, а значит есть смысл разобраться: что это такое и откуда проистекает польза при применении.

И вот тут начинается самое интересное. Ответ на первый вопрос “что это такое?” в целом не вызывает особой сложности (если подойти к делу формально и определить какие же преобразования добавляются в сетку), а вот про “откуда проистекает польза?” идут жаркие споры. Объяснение, авторов методики подвергается серьёзной критике.

Мне понравилось как это сформулировано в [3]:

“The practical success of BatchNorm is indisputable. By now, it is used by default in most deep learning models, both in research (more than 6,000 citations) and real-world settings. Somewhat shockingly, however, despite its prominence, we still have a poor understanding of what the effectiveness of BatchNorm is stemming from. In fact, there are now a number of works that provide alternatives to BatchNorm, but none of them seem to bring us any closer to understanding this issue.”

Правда, стоит отметить, что у нас всё глубокое обучение и нейронные сети во многом можно описать теми же словами. Оно вроде работает и мы даже, в принципе, понимаем какие рычаги жать, чтобы ехало в примерно нужном направлении, но многие моменты так до конца и не объясняются.

Заканчивая лирику переходим к конкретике. Начнем разбираться с самого начала, а именно классической статьи [1] где методика BN и была впервые описана.

Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift

Авторы уже в заголовке статьи [1] анонсируют, что ускорение тренировки связано с тем, что применение BN позволяет уменьшить internal covariate shift. Следовательно, есть смысл разобраться, что такое covariate shift (отложив пока в сторону, что значит internal), а для этого надо обратиться к статье [2] на которую ссылаются авторы [1].

Covariate shift

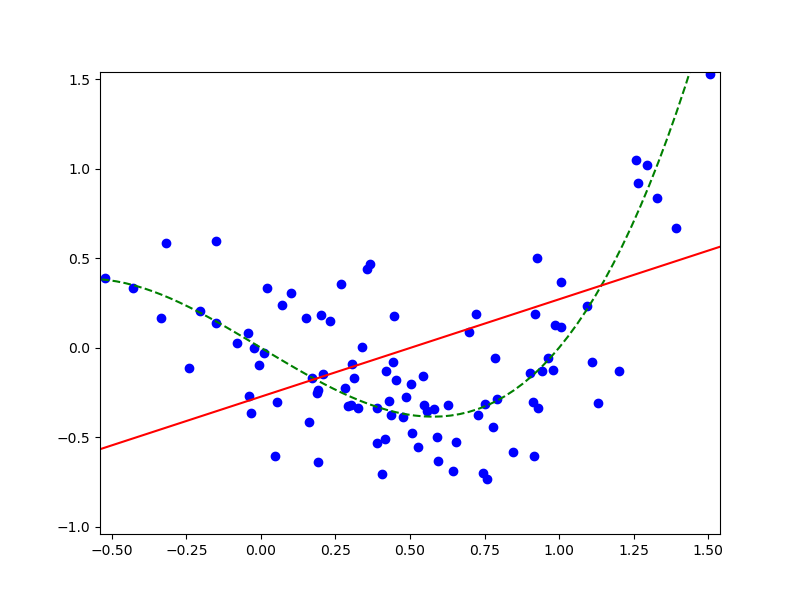
Рассмотрим следующий пример (который взят из той же [2]).

Пример

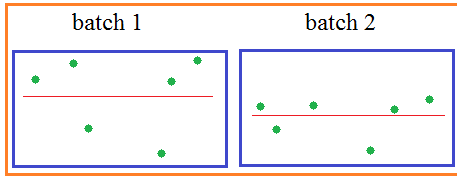
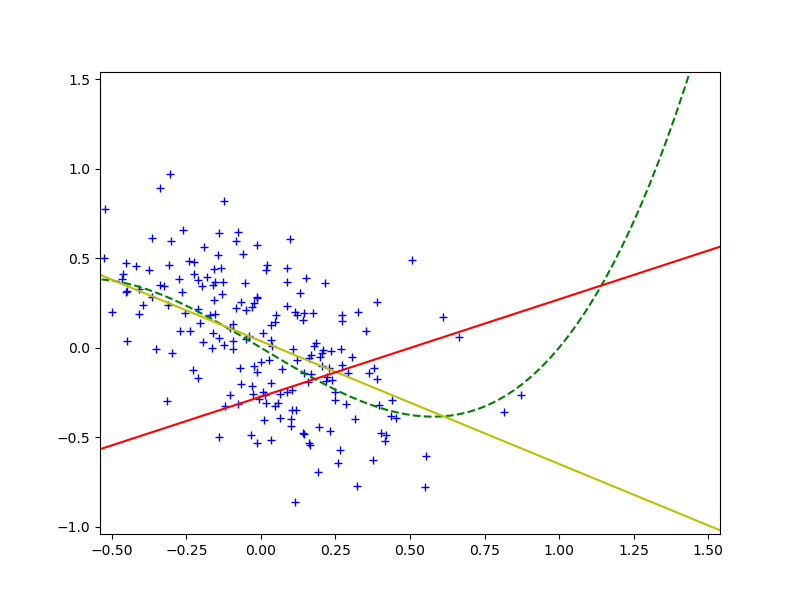
Коэффициенты определим методом наименьших квадратов (МНК), т.е. решив задачу оптимизации:

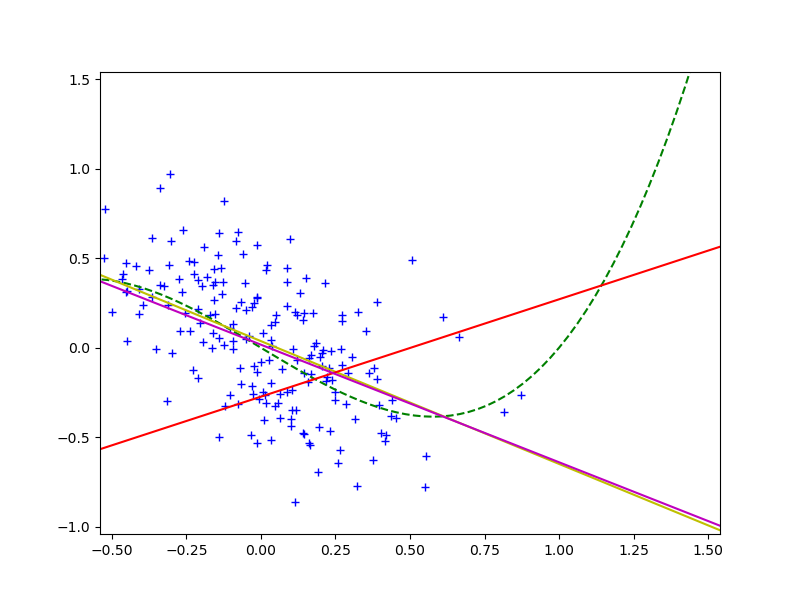
Очевидно, раз красная и желтая линии существенно не совпадают, то модель “наученная” по тренировочному набору для проверочного набора даёт плохой результат. В [2] предлагается, для того, чтобы погасить влияние covariate shift вместо МНК использовать взвешенный МНК, и оптимизировать функцию:

видно, что она практически совпадает с желтой, а значит мы действительно побороли covariate shift и улучшили предсказательную силу модели на проверочном наборе.

Batch Normalization. Определение.

Мы сейчас не будем углубляться в то, насколько действительно ICS оказывает влияние на скорость тренировки, и борется ли BN с ICS. Позже мы разберем статьи, которые к идеи с ICS относятся с большим скептицизмом и объясняют успех BN совсем другим. Но то, что BN отлично работает подтверждается на практике, поэтому переходим к его описанию

Если теоретическое обоснование BN выглядит “притянутым за уши” (во всяком случае в статье нет каких-то внятных экспериментов, которые бы указывали на то, что до добавления BN сеть страдала от ICS и вот вам статистика, а после перестала, и вот вам другая статистика), то какие практические соображения лежат в основе метода, авторы описывают весьма четко и понятно.

Пример.

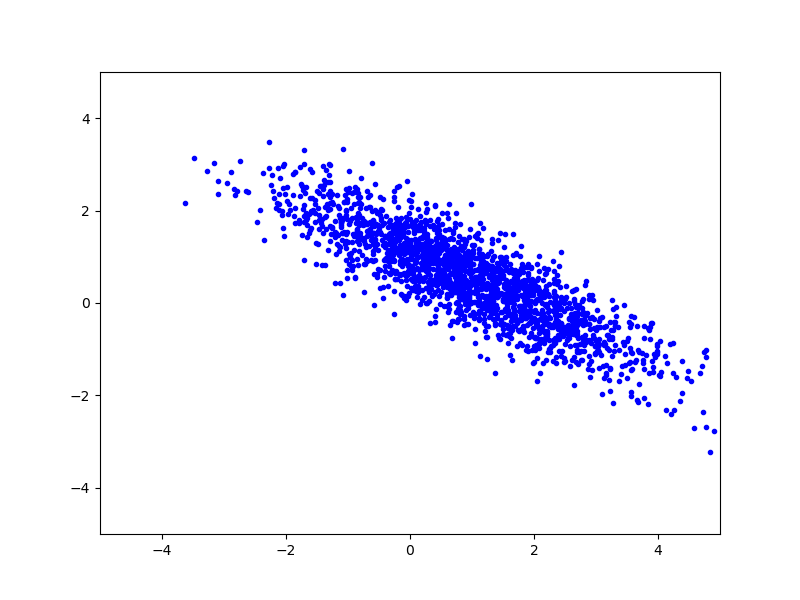
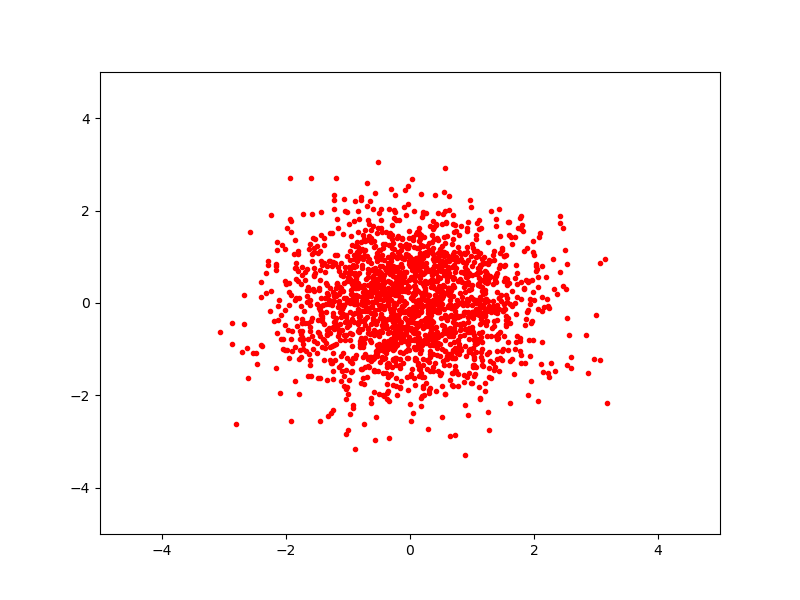
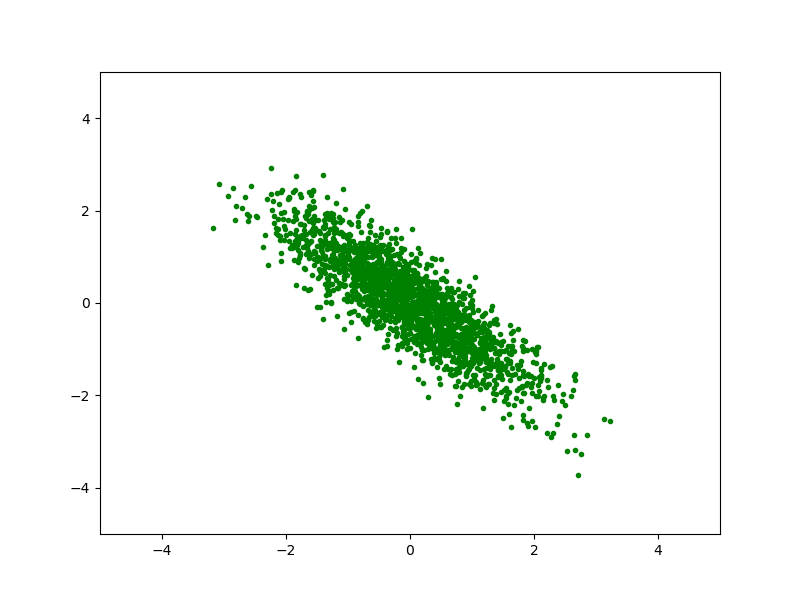
Сегенерируем некоторое количество векторов, подчиняющихся этому распределению и отрисуем их на плоскости:

Теперь найдем собственные числа и собственные вектора для матрицы ковариации (если бы мы не знали матрицу ковариации и среднее, то могли бы вычислить приближенное значение из набора векторов):

$\lambda_2 = 0.2, e_2 = (e_<21>, e_<22>) = (0.5547002, 0.83205029)$

и определим линейное преобразование:

Покончили с примером, смысл того, что предполагается сделать с данными понятен.

Второе, когда сеть используется для вывода, обычно у нас нет ни батчей ни даже минибатчей, поэтому среднее и дисперсию мы сохраняем из тренировки, для этого для каждой компоненты вектора входа каждого слоя мы запоминаем аппроксимированые математическое ожидание и дисперсию, считая скользящую среднюю математического ожидания и дисперсии по минибатчам в процессе тренировки.

Batch Normalization. Практика.

Итак, что такое BN мы определили, разберёмся как её применять. Обычно и полносвязный, и свёрточный слой можно представить в виде:

\[z = g(\textrm(W \cdot x))\]

Чтобы получить максимальный эффект от использования BN в статье [1] предлагается еще несколько изменений в процессе тренировки сети:

Увеличить learning rate. Когда в сеть внедрена BN можно увеличить learning rate и таким образом ускорить процесс оптимизации нейронной сети, при этом избежать расходимости. В сетях без BN при применении больших learning rate за счет увеличения амплитуды градиентов возникает расходимость.

Ускорить убывание learning rate. Поскольку при добавлении в сеть BN скорость сходимости увеличивается, то можно уменьшать learning rate быстрее. (Обычно используется либо экспоненциальное уменьшение веса, либо ступенчатое, и то и другое регулируется двумя параметрами: во сколько раз и через сколько итераций уменьшить learning rate, при применении BN можно сократить число итераций)

Более тщательно перемешивать тренировочные данные, чтобы минибатчи не собирались из одних и тех же примеров.

Резюмируя. Авторы статьи [1] предложили методику ускорения сходимости нейронной сети. Эта методика доказала свою эффективность, кроме того она позволяет применять более широкий интервал метапараметров тренировки (например, больший learning rate) и с меньшей аккуратностью подходить к инициализации весов сети. Объяснение данной методики основывается на понятии ICS, однако, каких-то существенных подтверждений того, что данный метод действительно позволяет погасить ICS и именно за счет этого улучшить процесс тренировки в статье я не нашел (возможно плохо искал). Есть только некие теоретические рассуждения, которые не выглядят (на мой взгляд) достаточно убедительно.

Литература

S. Ioffe, Ch. Szegedy, “Batch Normali;zation: Accelerating Deep Network Training by Reducing Internal Covariate Shift”, arXiv:1502.03167v3, 2015

H. Shimodaira, “Improving predictive inference under covariate shift by weighting the log-likelihood function.”, Journal of Statistical Planning and Inference, 90(2):227–244, October 2000.

Sh. Santurkar, D. Tsipras, A. Ilyas, A. Madry, “How Does Batch Normalization Help Optimization? (No, It Is Not About Internal Covariate Shift)”, arXiv:1805.11604v5, 2019

Источник