общее свойство фигур что это

Плоские геометрические фигуры: свойства и основные формулы

В статье описываются геометрические фигуры: определение, основные свойства и формулы.

Плоские геометрические фигуры:

Четырехугольник (общее для всех четырехугольников)

Квадрат

Прямоугольник

Параллелограмм

Трапеция

Треугольник

Окружность

Геометрические фигуры — это любое сочетание точек, линий и поверхностей. Геометрические фигуры разделяются на плоские и объемные.

Плоские геометрические фигуры — это фигуры, все точки которых лежат на одной плоскости. Объемные геометрические фигуры — это фигуры, не все точки которых лежат на одной плоскости.

Четырёхугольник

Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три точки не лежат на одной прямой.

Основные свойства:

В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны. Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.

Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°.Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.

Квадрат

Квадрат — правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.

Основные формулы:

Периметр: P=4a, где P-периметр, a-сторона
Площадь: S=a 2 или S=d 2 /2
Сторона и диагональ связаны соотношениями: a=d/√2, d=a√2
Радиус описанной окружности: R=d или R=a/√(2)
Радиус вписанной окружности: r=a/2

где a-сторона, d-диагональ, P-периметр, S-площадь
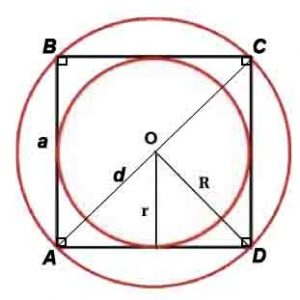
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(2) – корень квадратный из 2.

Свойства:

Прямоугольник

Прямоугольник — четырехугольник, у которого все углы прямые.

Основные формулы:

Периметр: P=(a+b)*2
Площадь по сторонам: S = a*b
Площадь по диагонали и углу между ними: S = d²* sin γ. / 2
Стороны и диагональ связаны соотношением: d=√(a 2 +b 2 )/2 (теорема Пифагора)
Радиус описанной окружности: R= √(a 2 +b 2 )/2 (теорема Пифагора)

где a, b — длины сторон прямоугольника, d-диагональ, P-периметр, S-площадь
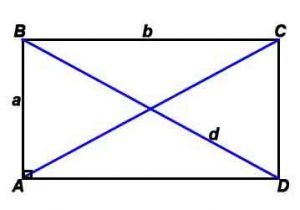
γ – угол между диагоналями
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(a 2 +b 2 ) – корень квадратный из (a 2 +b 2 ).

Свойства:

Параллелограмм

Параллелограмм — четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.

Определения:

Высота параллелограмма — это перпендикуляр, проведённый из вершины параллелограмма к противоположной стороне.

Основные формулы:

Стороны и диагональ связаны соотношением: (d₁) 2 +(d₂) 2 =(a 2 +b 2 )*2
Периметр: P=(a+b)*2
Площадь по стороне и высоте: S = a*h
S (Площадь) по двум сторонам и углу между ними: S=a*b*sin α
S (Площадь) по двум диагоналям и углу между ними: S=(d₁*d₂)/2*sin γ

где a, b — длины сторон, d₁, d₂ –диагонали, P-периметр, S-площадь,
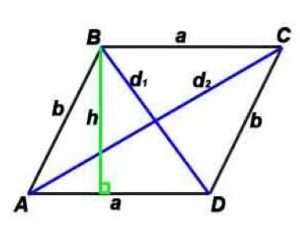
h-высота, проведенная к противоположной стороне
α — угол между сторонами параллелограмма,
γ — угол между диагоналями параллелограмма (острый).

Свойства:

Ромб

Ромб — это параллелограмм, у которого все стороны равны.

Основные формулы:

Периметр: P=4*a
Площадь по стороне и высоте: S=a*h
Площадь по диагоналям: S = (d₁*d₂)/2
Радиус окружности, вписанной в ромб: r=h/2 или r =(d₁*d₂)/4a
Площадь по стороне и радиусу вписанной окружности: S=2*a*r
Площадь по стороне и углу: S = a 2 · sin α

Свойства:

Трапеция

Трапеция — четырёхугольник, у которого только две противолежащие стороны параллельны.

Определения:

Основные формулы:

Периметр: P=a+b+c+d
Площадь определить: S=h*(a+b)/2
Стороны и диагональ равнобокой трапеции: d² = ab+c²
Радиус вписанной окружности: r = h/2

Свойства:

В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон (a+b=c+d). Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.

Треугольник

Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).

Определения:

Основные формулы:

Периметр: P=a+b+c
Площадь по стороне и высоте: S=(a*h)/2
Площадь: по сторонам и углу между ними: S=(a*b)/2* sin γ
по трем сторонам и радиусу описанной окружности: S=(a*b*c)/4R
по трем сторонам и радиусу вписанной окружности: S=(a+b+c)/2*r
Площадь прямоугольного треугольника: S=(a*b)/2
Стороны прямоугольного треугольника: c 2 =a 2 +b 2 (Теорема Пифагора)

Свойства:

Окружность

Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра окружности), которая лежит в той же плоскости, что и кривая.

Определения:

Основные формулы:

Длина окружности: L = 2πR
Площадь круга: S = π*r 2 или S = π*d 2 /4

где π = 3,14 (3,1415926535) – величина постоянная,
где r-радиус, d –диаметр, L – длина окружности, S-площадь.

Источник

Основные геометрические фигуры

Основные понятия

Основные геометрические фигуры на плоскости — это точка и прямая линия. А простейшие фигуры — это луч, отрезок и ломаная линия.

Минимальный объект в геометрии — точка. Ее особенность в том, что она не имеет размеров: у нее нет высоты, длины, радиуса. У точки можно определить только ее расположение, которое принято обозначать одной заглавной буквой латинского алфавита.

Из множества точек может получится линия, а из нескольких соединенных между собой линий — геометрические фигуры.

Каждая математическая фигура имеет собственную величину, которую можно измерить при помощи формул и внимательности.

Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.

Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской P.

Если параметры переданы в разных единицах измерения длины, нужно перевести все данные к одной единице измерения.

Популярные единицы измерения площади:

Геометрические тела — часть пространства, которая ограничена замкнутой поверхностью своей наружной границы.

Если все точки фигуры принадлежат одной плоскости, значит она является плоской.

Объемная фигура — геометрическая фигура, у которой все точки не находятся на одной плоскости.

Примеры объемных геометрических фигур:

Рассмотрим подробнее некоторые фигуры, разберем их определения и свойства.

Прямоугольник

Прямоугольник — четырехугольник, у которого все стороны пересекаются под прямым углом.

Узнать площадь прямоугольника помогут следующие формулы:

Диагональ — это отрезок, который соединяет противоположные вершины фигуры. Он есть во всех фигурах, число вершин которых больше трех.

Периметр прямоугольника — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

Квадрат

Квадрат — это тот же прямоугольник, у которого все стороны равны.

Найти площадь квадрата легко:

Периметр квадрата — это длина стороны, умноженная на четыре.

P = 4 × a, где a — длина стороны.

Трапеция

Трапеция — это четырехугольник, у которого две стороны параллельны, а две не параллельны.

Основное свойство: в трапецию можно вписать окружность, если сумма ее оснований равна сумме боковых сторон.

Как найти площадь трапеции:

S = (a + b) : 2 × h, где a, b — два разных основания, h — высота трапеции.

Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны и был расположен перпендикулярно к этим основаниям.

Формула периметра для равнобедренной трапеции отличается от прямоугольника тем, что у равнобедренной трапеции есть две равные стороны.

P = a + b + 2 × c, где a, b — параллельные стороны, c — две длины одинаковых сторон.

Параллелограмм и ромб

Параллелограмм — четырехугольник, противоположные стороны которого попарно параллельны

Ромб — это параллелограмм с равными сторонами.

Общие формулы расчета площади фигур:

Периметр ромба — это произведение длины стороны на четыре.

P = 4 × a, где a — длина стороны.

Периметр параллелограмма — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

Треугольник

Треугольник — это такая фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки принято называть вершинами, а отрезки — сторонами.

Рассчитать площадь треугольника можно несколькими способами по исходным данным, давайте их рассмотрим.

S = 0,5 × a × h, где a — длина основания, h — высота, проведенная к основанию.

Основание может быть расположено иначе, например так:

При тупом угле высоту можно отразить на продолжение основания:

При прямом угле основанием и высотой будут его катеты:

S = 0,5 × a × b × sinα, где a и b — две стороны, sinα — синус угла между ними.

S = (a × b × с) : 4 × R, где a, b и с — стороны треугольника, а R — радиус описанной окружности.

S = p × r, где р — полупериметр треугольника, r — радиус вписанной окружности.

Периметр треугольника — это сумма длин трех его сторон.

P = a + b + c, где a, b, c — длина стороны.

Формула измерения периметра для равностороннего треугольника — это длины стороны, умноженная на три.

P = 3 × a, где a — длина стороны.

Круг — это множество точек на плоскости, которые удалены от центра на равном радиусу расстоянии.

Окружность — это граница круга.

Радиус окружности — это расстояние от центра окружности до любой точки на ней.

Диаметр круга — это отрезок, который соединяет две точки на окружности и проходящий через ее центр. Диаметр круга равен двум его радиусам.

Формулы площади круга:

Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.

L = d × π = 2 × r × π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Источник

Общие и отличительные свойства объектов. 3-й класс

Класс: 3

Форма урока – диалог с опорой на знания и опыт учащихся, фронтальная работа (решение информационных задач в рабочей тетради)

Тип урока – урок объяснения

Стратегия – опережающая, развивающая.

Ход урока

1. Организационный момент

– Добрый день, ребята! Добрый день. уважаемые гости. Я хочу, чтобы у всех сегодня было доброе настроение. Давайте улыбнёмся друг другу. И будем по-доброму относиться друг к другу, по-доброму работать, мыслить. Не зря народная мудрость гласит:

“Где доброта, там красота”
– Пусть это станет девизом нашего урока!

2. Повторение материала предыдущей темы

а) – Предлагаю проверить домашнее задание и провести игру-разминку.

Правила игры следующие:

К доске выходят четыре ученика и получают карточки с названием предметов. Никто никому не говорит, какая карточка ему досталась. Я называю свойство, а ученики поднимают руки, если их объект этим свойством обладает. Затем мы должны будем отгадать, какой объект изображён на карточке у каждого из них. Договорились?

Яблоко
Арбуз
Машина
Самолёт

Свойства объектов:
круглый, может летать, съедобный, вкусный, сочный, гудит, перевозит людей, большой.

– Кто догадался, какой предмет у каждого ученика?
– Что помогло вам в этом (свойства предмета)

– человека;
– собаки;
– кошки.

Назовите несколько объектов, которые обладают свойством “круглый”, “прямоугольный”, “бумажный”, “стеклянный”.
Назовите какое-нибудь свойство объекта с именем “телевизор”, “магнитофон”, “компьютер”

3. Обобщение сведений, известных учащимся, с выходом на новый материал

– Как вы поняли из предыдущих уроков, у каждого объекта множество свойств. Но если мы будем сравнивать объекты между собой, то увидим, что свойства объекта бывают общими и отличительными. Этой теме и посвящён наш сегодняшний урок.

– Исходя из темы как думаете, какие информационные задачи мы сегодня будем решать, т. е. что нам предстоит делать?

– Посмотрите на экран и скажите, чем похожи самолёт и пароход? (Это средства передвижения, и то, и другое транспорт).
– Можно сказать, что это общее свойство данных объектов? (можно)
– А теперь скажите, чем они различаются? (Самолёт воздушный транспорт, а пароход – водный)
– Правильно, это их отличительные свойства: плавать по воде и летать по воздуху.
– Теперь давай те рассмотрим сразу несколько объектов – например, учеников нашего класса. Давайте все встанем. Какое общее свойство у всех? (Быть учениками, быть детьми).
– Теперь выделим из данной группы объекты с отличительным свойством “быть девочкой”. Девочки сядьте. Для девочек это свойство общее или отличительное? (Общее)
– Теперь выделим из группы девочек объекты, с отличительным свойством “быть выше всех”. Пусть такие девочки встанут. Это их отличительное свойство.
– Садимся на места. Давайте обсудим то, что мы наблюдали. Как видим, одно и то же свойство “быть девочкой” может быть и общим, и отличительным. Оно отличительное, когда группа девочек входит в более широкую группу объектов – в класс, в котором кроме них есть ещё и мальчики.
– Рассмотрим ещё один пример. Внимание на экран

– Как назвать одним понятием изображённые на слайде объекты?(геометрические фигуры)
– Решим такую задачу: выделим из представленных на этом рисунке геометрических фигур такие, которые имеют свойства “иметь углы”
– Это отличительное свойство выделенных фигур от остальных.
– Рассмотрим получившуюся новую группу:

– Заметим, что теперь свойство “иметь углы” уже не отличительное, а общее, поскольку все фигуры этой группы имеют углы.
– Теперь выделим из данной группы объекты с отличительным свойством “иметь ровно три угла”. Такой объект в этой группе один – треугольник. Слайд 8
– Проанализируем проделанную работу.
– Мы видим, что одно и то же свойство может быть либо общим для группы объектов, либо отличительным.
– Так свойство “иметь углы” является для квадратов, прямоугольников и треугольников общим. Это же свойство будет отличительным для квадратов, прямоугольников и треугольников, если в состав группы ввести круги и овалы.

4. Физкультминутка

5. Продолжение работы над темой урока с закреплением полученных знаний

– В нашей работе встретились такие ключевые понятия как

– Кто может дать определение этим понятиям? (ответы детей)
– А теперь давайте обратимся к учебнику и познакомимся с определением, которое даёт этим понятием Н.В. Матвеева

Работа с учебником (с. 95)

– Итак свойства объектов бывают общие и отличительные.

– Назовите хотя бы одно общее свойство у таких разных объектов, как луна и мяч.
– Назовите отличительные свойства данных объектов.
– А теперь посмотрим как эти знания могут помочь нам на других уроках, например на уроке русского языка.

– Объектами выступают слова: картина, квартира, корова
– Найдите общие и отличительные свойства.

(Общие свойства: все словарные слова,
все имена существительные,
все трёхсложные,
все начинаются с один. звука
все имеют окончание а
Отличаются безударными гласными а и о)

Литературное чтение: “Курочка Ряба”, “Теремок”, “Золотая рыбка”

(Общие свойства – одна жанровая
принадлежность – сказки
Отличия: по классификации)

– Попробуйте сами привести подобные задания например с числами (заготовка 3 12 15 18) Слайд 14

6. Психологическая пауза

Ох, как хочется трудиться!
Делать всё охота.
Чтоб трудом своим гордиться,
Пусть кипит работа.

Я и бодр, и силён,
Всю работу сделаю.
Свою волю покажу.
Слово для себя сдержу.

7. Выполнение заданий в рабочей тетради

с. 26–27, с. 30–31 (табличка)

8. Обобщение и закрепление. Подведение итогов

– А сейчас – заключительный разговор. Подведём итог нашей работе.
– Что узнали нового?
– Что получилось легко?
– В какие моменты урока испытывали трудности?
– Как вы сможете использовать свой новый опыт?

9. Комментарии к домашнему заданию

Выполнить упражнения в рабочей тетради к §16.

10. Рефлексия

Я работал с ______________ настроением.
Я _____________ доволен собой.
Я бы хотел стать более ____________.

– Дорогие ребята, мне хочется поблагодарить вас за активность и инициативу. Наша совместная работа заканчивается, но наше сотрудничество продолжается.
– Я хочу похлопать Насте, потому что мне понравилось, как она работала сегодня на уроке.
– Настя, а чья работа понравилась тебе? (Поочерёдно дети хлопают друг другу, пока весь класс не будет хлопать последнему ученику)

Источник