что значит значащая цифра
Значащие цифры
Смотреть что такое «Значащие цифры» в других словарях:
ЗНАЧАЩИЕ ЦИФРЫ — (значащие разряды), цифры числа, которые выражают его с требуемой точностью; последние цифры могут быть округлены. Так, число 2,871828, округленное до шести цифр, будет представлено как 2,87183; округленное до трех цифр как 2,87 … Научно-технический энциклопедический словарь
ЗНАЧАЩИЕ ЦИФРЫ — в приближенных вычислениях все цифры числа, начиная с первой слева, отличной от нуля, до последней, за правильность которой можно ручаться. Напр., в записи результата взвешивания 0,03020 кг значащими цифрами будут 3, 0, 2 и 0 … Большой Энциклопедический словарь
значащие цифры — в приближённых вычислениях, все цифры числа, начиная с первой слева, отличной от нуля, до последней, за правильность которой можно ручаться. Например, в записи результата взвешивания 0,03020 кг значащими цифрами будут 3, 0, 2 и 0. * * * ЗНАЧАЩИЕ… … Энциклопедический словарь
ЗНАЧАЩИЕ ЦИФРЫ — в приближённых вычислениях все цифры числа, начиная с первой слева, отличной от нуля, до последней, за правильность к рой можно ручаться. Напр., в записи результатов взвешивания 0,320 кг 3. ц. будут 3, 2 и 0 … Большой энциклопедический политехнический словарь
ЗНАЧАЩИЕ ЦИФРЫ — в приближённых вычислениях, все цифры числа, начиная с первой слева, отличной от нуля, до последней, за правильность к рой можно ручаться. Напр., в записи результата взвешивания 0,03020 кг значащими цифрами будут 3, 0, 2 и 0 … Естествознание. Энциклопедический словарь
Закон Бенфорда — Закон Бенфорда, или закон первой цифры, описывает вероятность появления определённой первой значащей цифры в распределениях величин, взятых из реальной жизни. Закон верен для многих таких распределений, но не для всех. Ра … Википедия
АРИФМЕТИКА — искусство вычислений, производимых с положительными действительными числами. Краткая история арифметики. С глубокой древности работа с числами подразделялась на две различные области: одна касалась непосредственно свойств чисел, другая была… … Энциклопедия Кольера
Логарифм — График двоичного логарифма Логарифм числа … Википедия
Метод одной касательной — Метод Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643 1727), под именем… … Википедия
Метод Ньютона — Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном… … Википедия
Значимые цифры: правила, примеры, решенные упражнения
Содержание:
А что происходит, когда число целое? Это означает, что он известен с максимально возможной точностью, другими словами, он имеет бесконечную точность. Например, при подсчете людей, животных или таких предметов, как книги и телефоны, результатом будет точное целое число.
Если мы скажем, что в кинотеатре 110 человек смотрят фильм, это точное число, ни много, ни мало, и оно состоит из трех значащих цифр.
Значительные числа обрабатываются по некоторым простым правилам, которые запоминаются после небольшой практики, как мы увидим дальше.
Правила определения значащих цифр числа
Правило 1
Начальные нули не считаются значащими цифрами, поэтому 0,045 и 4,5 имеют две значащие цифры, поскольку они начинают отсчет слева и начиная с первой ненулевой цифры.
Правило 2
Нули после (справа) первой значащей цифры действительно считаются значащей цифрой (если это оправдано точностью измерительного прибора).
Наконец, нули в середине также считаются значащей цифрой.
Правило 3
Для чисел, записанных в экспоненциальном представлении, все цифры в мантиссе значимы, а показатель степени не влияет на точность.
Правило 4
При выполнении операций с десятичными знаками, например при вычислении площадей или других подобных операций, результат должен иметь такое же количество значащих цифр, что и количество с наименьшим количеством значащих цифр, участвовавших в операции. Это правило действует для любых арифметических операций.
Правило 5
Знак числа не влияет на количество его значащих цифр.
Мы сразу же увидим некоторые примеры этого и всех других правил.
Примеры
Пример 1
Найдите, сколько значащих цифр в каждом из этих чисел.
Ответы
а) 876 имеет 3 значащих цифры.
б) 1000,68 имеет 6 значащих цифр, поскольку нули в середине считаются как таковые.
c) Вместо 0,00005026 имеется 4 значащих цифры. Обратите внимание, что 5 нулей слева от 5 не считаются значащими цифрами, тогда как 0 между 5 и 2 считается.
г) 4.8 имеет 2 значащих цифры.
Пример 2
Обычно измерения проводят с помощью измерительных инструментов, таких как рулетки, часы, термометры, весы и т. Д. Со сколькими значащими цифрами мы должны указывать количества, которые мы измеряем таким образом?
Ответить
Это зависит от оценки инструмента, которым он измеряется. Возьмем пример: измерьте внешний диаметр трубы с помощью градуированной линейки и штангенциркуля.
Он более точен, чем градуированная линейка, потому что с его помощью мы можем узнать более значащие числа определенной длины.
Вот почему нет смысла сообщать периметр, скажем, 35,88 см, если мы измеряем его рулеткой, поскольку этот инструмент недостаточно точен, чтобы указать такое количество значащих цифр.
Оценка рулетки A определяется по:
Пример 3
Сколько значащих цифр в показании цифрового термометра?
Ответить
Термометр на рисунке показывает трехзначные показания температуры. Однако в показанном измерении 36,6 ºC только первые две цифры слева направо являются точными, поскольку на десятичную дробь влияет погрешность оценки прибора, которая обычно указывается на задней стороне прибора или на ваше руководство по эксплуатации.
Обычно для представленного типа цифрового прибора погрешность оценки составляет 0,1 ºC. Этого достаточно, чтобы быть уверенным, что у вас нет температуры.
Правила округления чисел
При использовании калькулятора для выполнения расчетов с полученными измерениями некорректно давать результат, используя все цифры, которые появляются на экране.
Сохраняются только те, которые точно известны, поскольку только они имеют истинное значение. Затем необходимо округлить результаты, чтобы они соответствовали количеству точно известных цифр. Вот эти правила:
-Если число, следующее за цифрой, которую необходимо скрыть, является равно или больше 5, к этой цифре добавляется 1.
Например, при округлении 3,786 до двух десятичных знаков мы хотим сохранить числа до 8. Поскольку число, следующее за (6), больше 5, 8 становится 8 + 1 = 9, и число остается как 3.79.
-Когда число, следующее за цифрой, которую необходимо сохранить, менее 5, цифра останется прежней.
Если мы хотим округлить 1,27924, чтобы у него было только 3 десятичных разряда, это достигается путем достижения 9, за которым следует 2. Поскольку 2 меньше 5, эти десятичные дроби исчезают, а округленное число остается 1,279.
Упражнение решено
Обеденный стол имеет форму и размеры, указанные на прилагаемом рисунке. Вам предлагается рассчитать его площадь по правилам работы со значащими цифрами.
Решение
Зона стола может быть разделена на центральную прямоугольную зону и два полукруга, по одному с каждой стороны, которые вместе составляют один полный круг.
Мы будем называть A1 к площади прямоугольника, задаваемой:
К1 = основание × высота = 2,5 м x 1,0 м = 2,5 м 2
Со своей стороны, площадь круга, равная площади 1 полукруга, умноженной на 2, равна:
Диаметр любого из полукругов составляет 1,0 м, поэтому радиус равен 0,50 м. Диаметр также можно использовать напрямую для расчета площади, в этом случае:
К2 = (π × диаметр 2 ) / 4
К2 = [π x (1,0 м) 2 ] / 4 = 0,785398163 м 2
Были использованы все цифры, предоставленные калькулятором. Теперь добавляем A1 уже2 для общей площади стола A:
A = (2,5 + 0,785398163) м 2 = 3,285398163 м 2
Поскольку размеры таблицы известны до двух значащих цифр, не имеет смысла выражать результат со всеми десятичными знаками, указанными калькулятором, который никогда не дает количество значащих цифр в результате.
Что вам нужно сделать, так это округлить область так, чтобы в ней было такое же количество значащих цифр, что и размеры таблицы, то есть 2. Таким образом, окончательный результат будет представлен следующим образом:
Ссылки
Непрерывные процессы: характеристики, виды, примеры
Керамика Чавина: происхождение, характеристики, выдающиеся работы
значащие цифры
Смотреть что такое «значащие цифры» в других словарях:
ЗНАЧАЩИЕ ЦИФРЫ — (значащие разряды), цифры числа, которые выражают его с требуемой точностью; последние цифры могут быть округлены. Так, число 2,871828, округленное до шести цифр, будет представлено как 2,87183; округленное до трех цифр как 2,87 … Научно-технический энциклопедический словарь
ЗНАЧАЩИЕ ЦИФРЫ — в приближенных вычислениях все цифры числа, начиная с первой слева, отличной от нуля, до последней, за правильность которой можно ручаться. Напр., в записи результата взвешивания 0,03020 кг значащими цифрами будут 3, 0, 2 и 0 … Большой Энциклопедический словарь
Значащие цифры — в приближённых вычислениях, все цифры числа, начиная с 1 й слева, отличной от нуля, до последней, за правильность которой можно ручаться. Например, если измерение произведено с точностью до 0,0001 и дало результат 0,0320, то З. ц. будут 3 … Большая советская энциклопедия
ЗНАЧАЩИЕ ЦИФРЫ — в приближённых вычислениях все цифры числа, начиная с первой слева, отличной от нуля, до последней, за правильность к рой можно ручаться. Напр., в записи результатов взвешивания 0,320 кг 3. ц. будут 3, 2 и 0 … Большой энциклопедический политехнический словарь
ЗНАЧАЩИЕ ЦИФРЫ — в приближённых вычислениях, все цифры числа, начиная с первой слева, отличной от нуля, до последней, за правильность к рой можно ручаться. Напр., в записи результата взвешивания 0,03020 кг значащими цифрами будут 3, 0, 2 и 0 … Естествознание. Энциклопедический словарь
Закон Бенфорда — Закон Бенфорда, или закон первой цифры, описывает вероятность появления определённой первой значащей цифры в распределениях величин, взятых из реальной жизни. Закон верен для многих таких распределений, но не для всех. Ра … Википедия
АРИФМЕТИКА — искусство вычислений, производимых с положительными действительными числами. Краткая история арифметики. С глубокой древности работа с числами подразделялась на две различные области: одна касалась непосредственно свойств чисел, другая была… … Энциклопедия Кольера
Логарифм — График двоичного логарифма Логарифм числа … Википедия
Метод одной касательной — Метод Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643 1727), под именем… … Википедия
Метод Ньютона — Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном… … Википедия
ЗНАЧАЩАЯ ЦИФРА
— термин, относящийся к приближенному заданию действительного числа. Пусть в системе счисления с основанием qдля действительного числа хполучено приближенное представление q-ичной дробью
З. ц. at наз. верной, если абсолютная погрешность ( х* )числа х*, то есть величина |х- х*|, удовлетворяет неравенству
Обычно при приближенном задании числа химеет смысл указывать только верные З. ц.
Смотреть что такое «ЗНАЧАЩАЯ ЦИФРА» в других словарях:
значащая цифра — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN significant digitsignificant figurevalid digitnon zero digit … Справочник технического переводчика
наименьшая значащая цифра — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN least significant digitLSD … Справочник технического переводчика
Закон Бенфорда — Закон Бенфорда, или закон первой цифры, описывает вероятность появления определённой первой значащей цифры в распределениях величин, взятых из реальной жизни. Закон верен для многих таких распределений, но не для всех. Ра … Википедия
округление — я; ср. к Округлить округлять и Округлиться округляться. О. форм. О. сумм, капитала, дотаций. О. до двух тысяч. О. дроби. * * * округление числа, замена его числом, представляющим его приближённо. Округление производится постепенно справа налево… … Энциклопедический словарь
ОКРУГЛЕНИЕ — числа замена его числом, представляющим его приближенно. Округление производится постепенно справа налево по следующему правилу: когда последняя значащая цифра a?4, она просто отбрасывается; когда a?6, ближайшая слева от нее цифра увеличивается… … Большой Энциклопедический словарь
ОКРУГЛЕНИЕ — числа замена его числом, представляющим его приближённо. О. производится постепенно справа налево по след. правилу: когда последняя значащая цифра а= = 6, ближайшая слева от него цифра увеличивается на… … Большой энциклопедический политехнический словарь
ОКРУГЛЕНИЕ — числа, замена его числом, представляющим его приближённо. О. производится постепенно справа налево по след. правилу: когда последняя значащая цифра а 6, ближайшая слева от неё цифра увеличивается на… … Естествознание. Энциклопедический словарь
криптоарифм — Арифметическая задача, в которой вместо цифр используются буквы, причем: каждая цифра заменяется ровно на одну букву и встречается хотя бы раз; самая старшая значащая цифра любого числа не может быть нулем; если основание системы счисления… … Справочник технического переводчика
Фидонет — Запрос «Фидо» перенаправляется сюда; см. также другие значения. Фидонет (от англ. FidoNet, /ˈfaɪdəʊnɛt/; коротко Фидо) международная любительская компьютерная сеть, построенная по технологии «из точки в точку».[1] Изначально программное… … Википедия
Редактор сообщений Фидонет — Запрос «Фидо» перенаправляется сюда. Cм. также другие значения. Фидонет (коротко Фидо; от англ. Fidonet, /ˈfaɪdəʊnɛt/) международная некоммерческая компьютерная сеть, построенная по технологиям «из точки в точку» и «коммутация с запоминанием»[1] … Википедия
Следующие цифры не являются значащими цифрами.
Далее предполагается основание системы счисления 10.
СОДЕРЖАНИЕ
Определение значащих цифр
Правила определения значащих цифр в числе
Обратите внимание, что идентификация значащих цифр в числе требует знания того, какие цифры являются надежными (например, зная разрешение измерения или отчетности, с которой число получено или обработано), поскольку только надежные цифры могут быть значимыми; например, 3 и 4 в 0,00234 г не имеют значения, если измеряемый наименьший вес составляет 0,001 г.
Способы обозначения значащих цифр в целых числах с завершающими нулями
Значение конечных нулей в числе, не содержащем десятичной точки, может быть неоднозначным. Например, не всегда может быть ясно, является ли число 1300 точным с точностью до ближайшей единицы (просто случайно оказывается, что оно является точным кратным сотне) или оно отображается только с точностью до ближайших сотен из-за округления или неопределенности. Для решения этой проблемы существует множество соглашений. Однако они не используются повсеместно и будут эффективны только в том случае, если читатель знаком с соглашением:
Поскольку приведенные выше условные обозначения не являются общедоступными, для обозначения значимости числа с конечными нулями доступны следующие более широко признанные варианты:
Округление до значащих цифр
Чтобы округлить число до n значащих цифр:
В финансовых расчетах число часто округляется до заданного количества знаков. Например, до двух знаков после десятичного разделителя для многих мировых валют. Это делается потому, что большая точность несущественна, и обычно невозможно погасить задолженность меньше наименьшей денежной единицы.
В налоговых декларациях Великобритании доход округляется до ближайшего фунта, а уплаченный налог рассчитывается до ближайшего пенни.
В качестве иллюстрации десятичная величина 12,345 может быть выражена различным количеством значащих цифр или десятичных знаков. Если доступна недостаточная точность, то число округляется каким-либо образом, чтобы соответствовать имеющейся точности. В следующей таблице показаны результаты для различной общей точности при двух способах округления («Н / Д» означает «Неприменимо»).
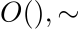 |
| Подгонка приближения |
| Концепции |
|---|
| Порядок аппроксимации Масштабный анализ · Обозначение Big O Подгонка кривой · Ложная точность Значимые числа |
| Прочие основы |
| Аппроксимация · Ошибка обобщения Полином Тейлора Научное моделирование |
| Точность | Округлено до значащих цифр | Округлено до десятичных знаков |
|---|---|---|
| 6 | 12,3450 | 12,345000 |
| 5 | 12,345 | 12,34500 |
| 4 | 12,34 или 12,35 | 12,3450 |
| 3 | 12,3 | 12,345 |
| 2 | 12 | 12,34 или 12,35 |
| 1 | 10 | 12,3 |
| 0 | N / A | 12 |
| Точность | Округлено до значащих цифр | Округлено до десятичных знаков |
|---|---|---|
| 7 | 0,01234500 | 0,0123450 |
| 6 | 0,0123450 | 0,012345 |
| 5 | 0,012345 | 0,01234 или 0,01235 |
| 4 | 0,01234 или 0,01235 | 0,0123 |
| 3 | 0,0123 | 0,012 |
| 2 | 0,012 | 0,01 |
| 1 | 0,01 | 0,0 |
| 0 | N / A | 0 |
Представление ненулевого числа x с точностью до p значащих цифр имеет числовое значение, которое задается формулой:
который может потребоваться написать с особой маркировкой, как описано выше, чтобы указать количество значащих нулей в конце.
Написание неопределенности и подразумеваемой неопределенности
Значимые цифры в письменной неопределенности
Подразумеваемая неопределенность
Арифметика
Поскольку существуют правила для определения значащих цифр в непосредственно измеряемых величинах, существуют также руководящие принципы (не правила) для определения значащих цифр в количествах, рассчитываемых на основе этих измеренных величин.
Приведенные ниже рекомендации предназначены для того, чтобы избежать получения более точного результата расчета, чем измеренные величины, но они не гарантируют, что полученная подразумеваемая погрешность достаточно близка к измеренным погрешностям. Эту проблему можно увидеть при преобразовании единиц измерения. Если в руководящих принципах подразумеваемая неопределенность слишком далека от измеренных, тогда может потребоваться определение значащих цифр, которые дают сопоставимую неопределенность.
Умножение и деление
Исключение
Сложение и вычитание
Правило вычисления значащих цифр для умножения и деления не то же самое, что правило для сложения и вычитания. Для умножения и деления имеет значение только общее количество значащих цифр в каждом из факторов при расчете; позиция последней значащей цифры в каждом множителе не имеет значения. Для сложения и вычитания имеет значение только позиция последней значащей цифры в каждом из членов вычисления; общее количество значащих цифр в каждом термине не имеет значения. Однако более высокая точность часто достигается, если в промежуточных результатах, которые используются в последующих вычислениях, сохраняются некоторые незначительные цифры.
Логарифм и антилогарифм
Основание 10 логарифм из нормализованного числа (то есть, × 10 б с 1 ≤ в б в виде целого числа), округляется таким образом, что его дробная часть ( так называемые мантиссы ) имеет столько же значащие цифры как значащие цифры в нормализованное число.
При вычислении антилогарифма нормализованного числа результат округляется, чтобы иметь столько значащих цифр, сколько значащих цифр в десятичной части числа, которое нужно антилогаринговать.
Трансцендентные функции
f (x))>> \ приблизительно <\ rm <(
Округлить только по окончательному результату расчета
При выполнении многоэтапных расчетов не округляйте результаты промежуточных расчетов; сохраняйте столько цифр, сколько возможно (по крайней мере, на одну цифру больше, чем позволяет правило округления для каждого этапа) до конца всех вычислений, чтобы избежать кумулятивных ошибок округления при отслеживании или записи значащих цифр в каждом промежуточном результате. Затем округлите окончательный результат, например, до наименьшего числа значащих цифр (для умножения или деления) или до самой левой позиции последней значащей цифры (для сложения или вычитания) среди входных данных в окончательном вычислении.
Оценка дополнительной цифры
При использовании линейки сначала используйте наименьшую отметку в качестве первой оценочной цифры. Например, если наименьшая отметка линейки составляет 0,1 см, а считывается 4,5 см, то это будет 4,5 (± 0,1 см) или 4,4–4,6 см относительно наименьшего интервала между отметками. Однако на практике размер обычно можно оценить на глаз ближе, чем интервал между наименьшей отметкой линейки, например, в приведенном выше случае его можно оценить как от 4,51 см до 4,53 см.
Также возможно, что общая длина линейки может быть неточной до степени наименьшей отметки, и отметки могут быть несовершенно разнесены в пределах каждой единицы. Однако, если принять нормальную линейку хорошего качества, должна быть возможность оценить десятые доли между ближайшими двумя отметками, чтобы получить дополнительный десятичный разряд точности. В противном случае ошибка чтения линейки добавляется к любой ошибке калибровки линейки.
Оценка в статистике
При оценке доли лиц, несущих определенную характеристику в популяции, из случайной выборки этой совокупности, количество значащих цифр не должно превышать максимальную точность, допускаемую этим размером выборки.


