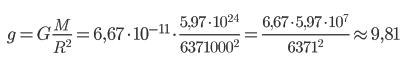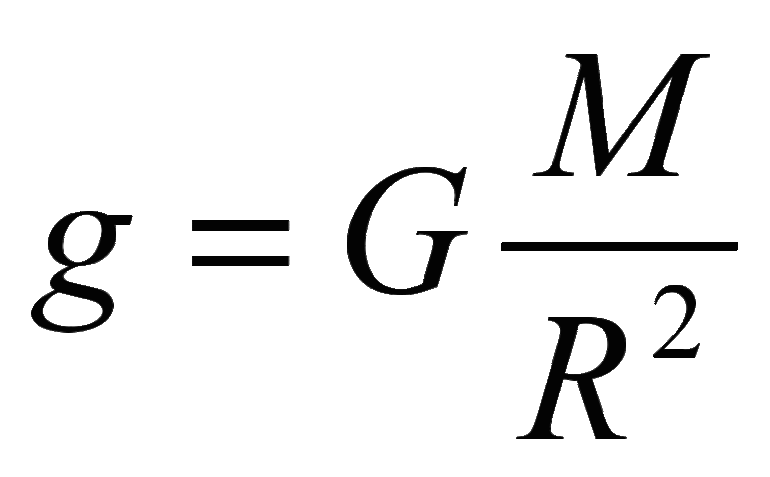что такое гравитационное ускорение
Ускорение свободного падения
Сила тяготения
В 1682 году Исаак Ньютон открыл закон всемирного тяготения. Он звучит так: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.
Формула силы тяготения согласно этому закону выглядит так:
Закон всемирного тяготения
F — сила тяготения [Н]
M — масса первого тела (часто планеты) [кг]
m — масса второго тела [кг]
R — расстояние между телами [м]
G — гравитационная постоянная
Когда мы встаем на весы, стрелка отклоняется. Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз.
Закон всемирного тяготения используют, чтобы вычислить силы взаимодействия между телами любой формы, если размеры тел значительно меньше расстояния между ними.
Если мы возьмем два шара, то для них можно использовать этот закон вне зависимости от расстояния между ними. За расстояние R между телами в этом случае принимается расстояние между центрами шаров.
Приливы и отливы существуют благодаря закону всемирного тяготения. В этом видео я рассказываю, что общего у приливов и прыщей. 🤓
Ускорение свободного падения
Чтобы математически верно и красиво прийти к ускорению свободного падения, нам необходимо сначала ввести понятие силы тяжести.
Сила тяжести — сила, с которой Земля притягивает все тела.
Сила тяжести
F = mg
F — сила тяжести [Н]
m — масса тела [кг]
g — ускорение свободного падения [м/с 2 ]
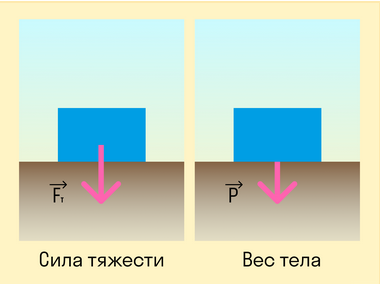
На первый взгляд сила тяжести очень похожа на вес тела. Действительно, в состоянии покоя на поверхности Земли формулы силы тяжести и веса идентичны. Вес тела в состоянии покоя численно равен массе тела, умноженной на ускорение свободного падения, разница состоит лишь в точке приложения силы.
Сила тяжести — это сила, с которой Земля действует на тело, а вес — сила, с которой тело действует на опору. Это значит, что у них будут разные точки приложения: у силы тяжести к центру масс тела, а у веса — к опоре.
Также важно понимать, что сила тяжести зависит исключительно от массы и планеты, на которой тело находится. А вес зависит еще и от ускорения, с которым движется тело или опора.
Например, в лифте вес зависит от того, куда и с каким ускорением двигаются его пассажиры. А силе тяжести все равно, куда и что движется — она не зависит от внешних факторов.
На второй взгляд сила тяжести очень похожа на силу тяготения. В обоих случаях мы имеем дело с притяжением — значит, можем сказать, что это одно и то же. Практически.
Мы можем сказать, что это одно и то же, если речь идет о Земле и каком-то предмете, который к этой планете притягивается. Тогда мы можем даже приравнять эти силы и выразить формулу для ускорения свободного падения:
Приравниваем правые части:
Делим на массу левую и правую части:
Это и будет формула ускорения свободного падения. Ускорение свободного падения для каждой планеты уникально.
Формула ускорения свободного падения
g — ускорение свободного падения [м/с 2 ]
M — масса планеты [кг]
R — расстояние между телами [м]
G — гравитационная постоянная
Ускорение свободного падения характеризует то, как быстро увеличивается скорость тела при свободном падении.
Свободное падение — это ускоренное движение тела в безвоздушном пространстве, при котором на тело действует только сила тяжести.
Ускорение свободного падения на разных планетах
Выше мы уже вывели формулу ускорения свободного падения. Давайте попробуем рассчитать ускорение свободного падения на планете Земля.
Для этого нам понадобятся следующие величины:
Подставим значения в формулу:
И кому же верить?
Ниже представлена таблица ускорений свободного падения и других характеристик для планет Солнечной системы, карликовых планет и Солнца.
Небесное тело
Ускорение свободного падения, м/с 2
Диаметр, км
Расстояние до Солнца, миллионы км
Масса, кг
Соотношение с массой Земли
Sep. 8th, 2014
Я, конечно, не могу объяснить, что такое гравитация, т.к. в настоящее время не имеется более общей теории, из которой гравитация получается как следствие. Речь пойдет о гравитационном поле в рамках Общей Теории Относительности А.Эйнштейна (в меру моего разумения).
Сначала разберем, что мы испытываем, когда говорим, что нас притягивает Земля. Мы испытываем действие ускорения, интерпретируемое в данном случае как действие гравитации Земли. Тут надо различить два разных случая: первый – двигаться с ускорением, второй – испытывать ускорение. Первый случай чисто кинематический – в какой-то системе отсчета некое тело движется с переменной скоростью. Кинематическое ускорение есть изменение скорости (как по величине, так и по направлению) в единицу времени. Поэтому тело, движущееся с переменной скоростью, движется с ускорением.
Другое дело испытывать ускорение. Это значит, что телу, что бы оставаться в покое приходится прикладывать какую-то силу, и, соответственно, к телу также прикладывается сила обычно называемая силой реакции опоры. Именно это ускорение измеряется акселерометром, который в простейшем случае представляет собой грузик на пружинке. Если ускорения нет, то пружинка не растянута. Если тело испытывает ускорение, то грузик, оставаясь неподвижным относительно этого тела, растянет пружинку. Фактически, пружинка создает силу, которая тянет грузик так, что он испытывает тоже ускорение, что и тело. Такое ускорение, измеренное акселерометром, будем называть собственным ускорением.
Приведем примеры. Возьмем ракету, которая движется с включенными двигателями далеко от всяких масс, создающих гравитационное поле. Рассмотрим движение в инерциальной системе отсчета (ИСО). Напомним, что ИСО является такая система отсчета (СО), в которой выполняется закон инерции, т.е. тело на которое не действуют силы сохраняет свою скорость (в т.ч. состояние покоя). В данном случае в качестве ИСО подойдет СО связанная, например, с ракетой с неработающими двигателями. В этой ИСО кинематическое ускорение ракеты будет совпадать с собственным ускорением, рисунок 1. Но, например, в СО ракеты с работающими двигателями, другая ракета будет иметь кинематическое ускорение, но ее собственное ускорение останется равным нулю, рисунок 2.
рисунок 1
рисунок 2
Рассмотрим тело, которое неподвижно в СО, связанной с Землей. Оно испытывает силу тяжести и имеет собственное ускорение, равное ускорению свободного падения. Тогда как его кинематическое ускорение отсутствует. Наоборот, тело, свободно падающее на Землю, имеет кинематическое ускорение (снова равное ускорению свободного падения:)), но не имеет собственного ускорения.
На сознательно внесенной путанице между различными ускорениями была построена ранее предложенная загадка:
«Возьмем две машины, скажем Порше 911 и ЗАЗ 965 (горбатый), машины одинаковые: багажник спереди, двигатель с воздушным охлаждением сзади, задний привод, две двери. На обе машины поставим по акселерометру, который измеряет ускорение. Сразу убедимся, что Порш способен развить большее ускорение, чем Запор. Если они начнут играть в догонялки, то Порше уедет далеко вперед от Запорожца. А если их связать ниточкой, то они эту ниточку порвут. Это присказка.
Возьмем два тела, на каждое тело опять поставим по акселерометру. Свяжем тела ниточкой. Обнаружим, что акселерометры показывают ускорение, направленное вдоль ниточки в одну и ту же сторону, но разное по абсолютной величине. Однако ниточка не рвётся. Как такое может быть?»
В первой части задачи речь идет о кинематическом ускорении, а во второй части о собственном. Они равны в ИСО. Но ведь нигде не сказано, что второй случай непременно должен быть в ИСО. Возьмем к примеру два тела прикрепленные вдоль радиуса на вращающемся диске и натянем между ними ниточку. Они оба имеют собственное ускорение вдоль ниточки, причем разное, но ниточка, разумеется, не порвется. Или можно взять два тела закрепленных друг над другом по вертикали. Ускорение свободного падения уменьшается с высотой, поэтому собственные ускорения этих тел различны, но они неподвижны друг относительно друга, как и тела на вращающемся диске.
Поэтому, когда мы говорим, что испытываем силу тяжести, то это значит, что мы имеем собственное ускорение. А если мы свободно движемся под действием силы тяжести (падаем или летим по баллистической траектории), то мы не имеем собственного ускорения и, как говорят, находимся в состоянии невесомости. Хотя, в последнем случае мы имеем кинематическое ускорение относительно Земли.
Таким образом, собственное ускорение возникает либо под действием гравитации, либо в результате ускорения тела в ИСО. Принцип эквивалентности Эйнштейна утверждает, что невозможно отличить одну причину ускорения от другой, если рассматривать область достаточно малых размеров.
Если различные тела неподвижны друг относительно друга и двигаются с одинаковым ускорением в ИСО, то каждое из них движется под действием силы, пропорциональной их массе (ускорение ведь одно и тоже). Если тела неподвижны в некой СО, в которой существует гравитационное поле, то действующая на них сила тяжести пропорциональна их массе. Первая из упомянутых масс связана с инерцией тела (чем больше масса, тем большую силу надо приложить, что бы создать тоже ускорение) и называется инертной массой. Вторая связана с гравитацией и есть коэффициент пропорциональности между величиной силы тяжести и гравитационным полем, подобно тому, как электрический заряд есть коэффициент пропорциональности между величиной электрического поля и силы действующей на заряженное тело. Такая масса называется гравитационной массой. Из принципа эквивалентности немедленно получается, что эти массы равны (точнее пропорциональны, но выбором единиц измерения их всегда можно сделать равными). В настоящее время их равенство установлено с очень высокой точностью. А часто, особенно в «школьной» физике об этой разной природе массы даже не задумываются и везде используют просто массу.
Рассмотрим теперь, как ускорение влияет на ход часов. Будем считать, что наличие собственного ускорения одинаково влияет на часы различной конструкции, т.е. в одном месте неподвижные друг относительно друга часы остаются синхронизованными независимо от величины собственного ускорения. Разумеется, большие ускорения могут повлиять на ход часов, в том числе и таким драматическим образом, как разрушение этих часов:). Но мы тут будем рассматривать часы, которые не ломаются и не портятся под действием ускорения. Тогда такие «хорошие» часы как раз и отмеряют то, что мы обычно называем временем*. Учитывая вышесказанное, под часами здесь можно понимать любое изменение во времени, в т.ч. и, например, изменения в организме человека.
Почти все специально сконструированные часы основаны на подсчете числа периодов некого периодического процесса. Пусть два наблюдателя**, которых мы по традиции назовем Боб и Алиса, снабжены идентичными часами и обмениваются сигналами в виде электромагнитных (ЭМ) волн, период которых совпадает (для простоты) с периодом колебаний в часах. Если они неподвижны в некой ИСО и, следовательно, неподвижны друг относительно друга, то они ничего интересного не обнаружат. Сигналы, которые они посылают друг другу остаются синхронизованными с ходом их часов. Если они движутся друг относительно друга, то такая синхронизация нарушается и замечательно описывается формулами Специальной теории относительности.
Иная ситуация получается, когда Боб и Алиса имеют собственное ускорение, но при этом остаются неподвижными друг относительно друга. Рассмотрим ее с обеих эквивалентных сторон. Пусть собственное ускорение вызвано гравитацией. Пусть Алиса находится сверху и посылает ЭМ сигнал вниз к Бобу. Но фотон, падая в гравитационном поле, приобретает энергию. (Если бы энергия фотона не менялась, то на основании этого можно было бы создать вечный двигатель.) А энергия фотона пропорциональна его частоте, поэтому Боб примет сигнал на более высокой частоте, рисунок 3.
рисунок 3
Пусть Боб и Алиса находятся на разных концах некого ящика, который движется с ускорением в ИСО (например, в ракете с работающими двигателями). Тогда Боб встретит сигнал, посланный Алисой, при большей скорости, чем была у Алисы, когда она этот сигнал посылала, рисунок 4. Поэтому, в силу эффекта Доплера, он примет сигнал на большей частоте.
В общем, в любом случае сигнал, принятый Бобом, будет иметь большую частоту и будет для него короче, чем то, что послала Алиса. И, разумеется, наоборот, если Боб посылает сигнал Алисе, то она его примет на меньшей частоте. Для оптических сигналов это соответствует смещению в красную область спектра. Поэтому говорят о гравитационном красном смещении, которое возникает, когда излучение идет от массивного объекта.
рисунок 4
Предположим, что Боб с Алисой договорились, что она будет начинать посылать сигнал, когда будет садиться завтракать, и выключать его, когда будет начало обеда. И время между завтраком и обедом у Алисы всегда одно и тоже, скажем один миллиард колебаний в сигнале. Боб принимает эти миллиард колебаний, но видит, что частота сигнала стала выше, и по его часам прошло меньше, чем миллиард колебаний. Боб тоже по своим часам обедает через миллиард колебаний после завтрака. Он связывается с Алисой, и она ему подтверждает, что между обедом и завтраком у нее проходит по ее часам также миллиард колебаний. На всякий случай они встречаются в одной точке и убеждаются, что их часы исправны и по-прежнему ходят в одном темпе. Но как только они разойдутся, то снова видят, что у Алисы с точки зрения Боба время между обедом и завтраком меньше чем у него. То, что взяли в качестве примера временной интервал между завтраком и обедом, есть условность. Понятно, что и любые другие процессы у Боба и Алисы будут протекать в разном темпе. Если у Боба и у Алисы нечто происходит за одно и тоже время по их собственным часам, то у Боба это происходит медленнее. Это и означает, что собственное время у Боба течет медленнее, чем у Алисы. С
Получается, что если тела испытывают собственное ускорение и находятся в разных местах в направлении этого ускорения, то у каждого тела будет свое собственное время. При этом у тела, которое находится ниже (с точки зрения ускорения, создаваемого гравитацией), время течет медленнее. Т.е. часы, связанные с телом и показывающие его собственное время будут идти у нижнего тела медленнее, чем у верхнего.
Таким образом, под гравитацией можно понимать следующее. Некая масса так искажает около себя пространство-время, что теперь время зависит еще и от пространственных координат, т.е. «течет» в разных местах по-разному. Поэтому еще говорят о местном времени, т.е. о времени, которое отсчитывается часами, расположенными в данном месте. Вот такое искажение (искривление) пространства-времени соответствует тому, что тела имеют собственное ускорение. Наличие этого ускорения воспринимается нами как сила тяжести. Что бы этого собственного ускорения не было, тело должно свободно двигаться в этом гравитационном поле.
Вообще говоря, массы так возмущают пространство-время, что искривленным становиться и пространство само по себе, а не только 4-мерное пространство-время.
Наличие местного времени для каждой точки пространства делает важным выбор системы координат. Например, необходимо рассчитывать положения во времени космических тел и космических аппаратов в Солнечной системе. Вопрос, а какое время использовать в результатах этих расчетов, если при наличии гравитационных полей оно в разных местах разное. Сейчас договорились, что в качестве координатного времени можно использовать, например, время в центре масс Солнечной системы (Barycentric Coordinate Time, Барицентрическое координатное время, TCB). Это время идет несколько быстрее, чем на поверхности Земли, примерно на 0,5 секунды за год.
Современный атомные часы достигли столь высокой точности, что для сравнения их показаний приходится вводить поправку, учитывающую положение часов в различных лабораториях над уровнем моря, и, следовательно, разницу в местном времени, вызываемую гравитацией Земли.
В следующей части планирую проиллюстрировать здесь сказанное с помощью формул.
* Это тонкий вопрос, что же измеряют часы. Ведь ни одни часы не обладают абсолютной точностью. Поэтому мне остается лишь согласиться с Ньютоном по поводу той физической величины, которая используется в физике и называется временем: «Абсолютное, истинное математическое время само по себе и по самой своей сущности, без всякого отношения к чему-либо внешнему, протекает равномерно и иначе называется длительностью. Относительное, кажущееся или обыденное время есть или точная, или изменчивая, постигаемая чувствами, внешняя, совершаемая при посредстве какого-либо движения, мера продолжительности, употребляемая в обыденной жизни вместо истинного математического времени, как-то: час, день, месяц, год. … Абсолютное время различается в астрономии от обыденного солнечного времени уравнением времени. Ибо естественные солнечные сутки, принимаемые при обыденном измерении за равные, на самом деле между собою неравны. Это неравенство и исправляется астрономами, чтобы при измерениях движений небесных светил применять более правильное время. Возможно, что не существует (в природе) такого равномерного движения, которым время могло бы измеряться с совершенной точностью.»
** Необходимо отметить, что привлечение антропоморфных наблюдателей, да и наблюдателей вообще, здесь и в подобных рассуждениях не является необходимым. Это обычно делается для придания образности и популярному изложению, т.к. человеку проще воспринимать человеческую точку зрения. Однако это может и вводить в заблуждение, что впрочем возможно для любого популярного изложения.
История открытия
Учёные Древней Греции разделяли любое движение на два типа: естественное и принудительное. Перемещение тела под воздействием гравитации считалось естественным, так как не имело видимой причины и происходило само собой.
Аристотель считал, что скорость падения напрямую зависит от массы. Это ошибочное утверждение родилось в результате примитивных наблюдений. Философ приводил в пример движение к земле яблок и листьев. Очевидно, что последние летели гораздо медленнее. Исследователи тех времён ещё очень мало понимали в физике. Такие понятия, как сопротивление воздуха и ускорение были неизвестны.
Утверждения Аристотеля считались неоспоримым постулатом вплоть до начала XVII века. Галилео Галлилей решительно отверг древнюю классификацию движения. В результате проведения нескольких опытов с движением тела по наклонной плоскости, учёный ввёл понятие ускорения.
Определение ускорения свободного падения в физике
Основное внимание Галлилей уделял изучению процесса свободного падения. Самым знаменитым стал эксперимент, проведённый на Пизанской башне.
С сооружения высотой 60-м были одновременно сброшены два предмета:
Результат был просто ошеломляющим. Оба тела достигли земли практически одновременно, а небольшая разница была объяснена силой сопротивления воздушной среды. Надо заметить, что наука тех лет существенно отличалась от сегодняшней. Считалось, что воздух не мешает падению, а, напротив, увеличивает его скорость.
Ещё одним заблуждением того времени было утверждение о том, что любое движение со временем прекращается, даже если на его пути нет преград. Галлилей опроверг и этот ошибочный закон физики, введя определение инерции.
В XVI веке ещё не существовало точных хронометров. Из-за этого ускорение падения тел с Пизанской башни было рассчитано довольно грубо. Для более точного измерения учёный изучал равноускоренное движение шарика по наклонной плоскости. А более или менее правильное значение ускорения сумел вычислить Гюйгенс в 1660 г.
Физическая сущность
Свободным падением может называться равноускоренное движение тела в результате действующей на него силы тяжести, происходящее в вакууме. Атмосфера Земли способна тормозить ускорение и замедлять падающие предметы. Однако, если величина сопротивления воздуха небольшая, ей можно пренебречь. К примеру, в опыте Галилея на башне в Пизе использовались шарообразные предметы, обладающие аэродинамичной формой. В результате этого коэффициент торможения удалось свести к минимуму.
Ускорение у поверхности Земли не зависит от массы предмета — это постоянная величина, обозначающаяся латинской буквой g и составляющая 9,80665 м/с.^2. Из-за воздействия центробежных сил на экваторе его значение немного меньше, а на полюсах, соответственно, больше.
Величина ускорения свободного падения зависит от нескольких факторов:
Вектор свободного падения всегда направлен вниз. Это можно наглядно увидеть, подбросив какой-либо предмет. Благодаря воздействию ускорения, его движение будет постепенно замедляться. Затем оно полностью остановится и направится в обратную сторону.
Формулы для расчёта
Галилей понимал, что исследование падения тел с Пизанской башни является несовершенным. Был поставлен новый эксперимент, в котором учёному удалось увеличить время движения и уменьшить сопротивление воздуха. Отполированные латунные шарики скатывались по желобам, расположенным под определённым углом наклона. В результате были выведен физический закон, согласно которому все падающие тела движутся с одинаковой, постоянно увеличивающейся скоростью.
Формула для нахождения: g=G (M/R ^ 2), где:
При помощи этой зависимости можно рассчитать значение g на поверхности любой планеты во вселенной.
Существуют задачи, для решения которых необходим более точный расчёт. В таком случае используется другая, расширенная формула: g=G (M/(R2+h)), где h — это высота над поверхностью планеты.
Стоит помнить, что для максимальной точности расчётов придётся учитывать большое количество факторов. Ускорение может измеряться при помощи специального прибора — гравиметра.
Ускорение на других планетах
Как видно из формулы, гравитационное ускорение напрямую зависит от массы и радиуса планеты. Из этого следует, что значение g на других планетах будет отличаться от земного.
Таблица показателя ускорения g для основных объектов Солнечной системы.
| Наименование | Ускорение, м/с. 2 |
| Солнце | 274,01 |
| Венера | 8,87 |
| Земля | 9,81 |
| Марс | 3,72 |
| Юпитер | 25,8 |
| Сатурн | 11,54 |
| Уран | 9,04 |
| Меркурий | 3,73 |
| Нептун | 11,33 |
| Луна | 1,69 |
Солнце является самым большим объектом в солнечной системе, его масса почти в 300 тыс. раз больше земной. Но как можно заметить из таблицы, ускорение на поверхности звезды превышает земное всего в 28 раз. Это объясняется огромным радиусом светила.
Во вселенной существуют очень компактные объекты с невероятной плотностью и чудовищным притяжением. Если взять среднюю нейтронную звезду с радиусом 13 км и массой 2,5*10 30 кг, то ускорение на её поверхности превысит земное в 100 млрд раз и составит довольно внушительное число — 9,87*10^11м/с. 2
Воздействие перегрузок на человека
Благодаря научно-техническому прогрессу и стремительному развитию технологий, современный человек имеет возможность пользоваться довольно быстрыми средствами передвижения. Чтобы попасть в любую точку планеты на самолёте, потребуется не более суток. Быстрая скорость передвижения неминуемо связана с таким понятием, как перегрузка.
Любая перегрузка являет собой отношение двух ускорений:
За единицу измерения принято брать гравитационное ускорение на Земле — 9,80665 м/с². Таким образом, нулевую перегрузку можно ощутить на себе лишь в невесомости.
Перегрузка является векторной величиной. Для людей и других живых организмов огромное значение имеет её направление. Это связано с тем, что организм приспособлен к постоянному воздействию гравитационного ускорения.
Характер положительной перегрузки заключается в том, что её вектор направлен вниз — от головы к ногам. Кровь оттекает от мозга и при показателе более 10 g человек может потерять сознание за считаные секунды. При отрицательном значении кровь, напротив, бьёт в голову. Это переносится гораздо хуже и может привести к кровоизлиянию и смерти.
Показатель перегрузки для различных ситуаций:
Военным и спортивным лётчикам приходится постоянно испытывать большие перегрузки. Для уменьшения вредного воздействия на организм существуют специальные защитные костюмы.
Переносить перегрузку лучше всего лёжа на спине. Именно в таком положении находятся космонавты при взлёте ракет.