что такое гравитационная масса
Масса гравитационная
Ма́сса — одна из важнейших физических величин. Первоначально (XVII–XIX века) она характеризовала «количество вещества» в физическом объекте, от которого, по представлениям того времени, зависели как способность объекта сопротивляться приложенной силе (инертность), так и гравитационные свойства — вес. В современной физике понятие «количество вещества» имеет другой смысл, а под массой понимают два различных свойства физического объекта:
Теоретически, гравитационная и инертная масса равны, поэтому в большинстве случаев просто говорят о массе, не уточняя какую из них имеют в виду.
Масса тела не зависит от того, какие внешние силы и в какой момент на это тело действуют.
Содержание
Исследование единства понятия массы
Гравитационная масса — характеристика материальной точки при анализе в классической механике, которая полагается причиной гравитационного взаимодействия тел, в отличие от инертной массы, которая определяет динамические свойства тел.
Как установлено экспериментально, эти две массы пропорциональны друг другу. Не было обнаружено никаких отклонений от этого закона, поэтому новых единиц измерения для инерционной массы не вводят (используют единицы измерения гравитационной массы) и коэффициент пропорциональности считают равным единице, что позволяет говорить и о равенстве инертной и гравитационной масс.
Можно сказать, что первая проверка пропорциональности двух видов массы была выполнена Галилео Галилеем, который открыл универсальность свободного падения. Согласно опытам Галилея по наблюдению свободного падения тел, все тела, независимо от их массы и материала, падают с одинаковым ускорением свободного падения. Сейчас эти опыты можно трактовать так: увеличение силы, действующей на более массивное тело со стороны гравитационного поля Земли, полностью компенсируется увеличением его инертных свойств. Следовательно, гравитационная масса пропорциональна инертной массе [1]
На равенство инертной и гравитационной масс обратил внимание ещё Ньютон, он же впервые доказал, что они отличаются не более чем на 0,1 % (иначе говоря, равны с точностью до 10 −3 ).. На сегодняшний день это равенство экспериментально проверено с очень высокой степенью точности (3×10 −13 ).
Фактически, равенство гравитационной и инертной масс было сформулировано А. Эйнштейном в виде слабого принципа эквивалентности — составной части принципов эквивалентности, положенных в основу общей теории относительности. Существует также сильный принцип эквивалентности — по которому в свободно падающей системе локально выполняется специальная теория относительности. Он на сегодняшний день проверен со значительно меньшей точностью.
В классической механике — масса есть величина аддитивная (масса системы равна сумме масс составляющих её тел) и инвариантная относительно смены системы отсчёта. В релятивистской механике масса неаддитивная величина, но тоже инвариантная, и хотя здесь под массой понимается абсолютная величина 4-вектора энергии-импульса, лоренц-инвариантная.
Определение массы
В СТО масса тела m определяется из уравнения релятивистской динамики [3] :
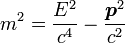
где E — полная энергия свободного тела, p — его импульс, c — скорость света.
Определённая выше масса является релятивистским инвариантом, то есть она одна и та же во всех системах отсчёта. Если перейти в систему отсчёта, где тело покоится, то 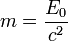
Следует однако отметить, что частицы с нулевой инвариантной массой (фотон, гравитон…) двигаются в вакууме со скоростью света (c ≈ 300000 км/сек) и поэтому не обладают системой отсчёта, в которой бы покоились.
Масса составных и нестабильных систем
Инвариантная масса элементарной частицы постоянна, и одинакова у всех частиц данного типа и их античастиц. Однако, масса массивных тел, составленных из нескольких элементарных частиц (например, ядра или атома) может зависеть от их внутреннего состояния.
Для системы, подверженной распаду (например, радиоактивному), величина энергии покоя определена лишь с точностью до постоянной Планка, делённой на время жизни: 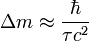
Единицы массы
В системе СИ масса измеряется в килограммах. В системе СГС используются граммы. Иногда используются также другие единицы измерения массы.
Формулы массы в физике. Инерционная и гравитационная массы. Относительная атомная масса. Масса и энергия
Масса является одним из важных свойств материи. Это понятие применяют при решении задач различного характера, начиная от проблем в механике и заканчивая химическими расчетами. Рассмотрим в статье, с помощью каких формул массу в физике можно рассчитать.
Что это такое?
Прежде чем приводить формулы массы в физике, дадим ей определение. Этим термином называется физическая величина, которая пропорциональна количеству материи, заключенной в данном теле. Следует не путать ее с количеством вещества, которое выражается в молях. Масса в СИ вычисляется в килограммах. Другими ее единицами являются тонны и граммы.

Масса бывает двух важных видов:
Первый вид рассматриваемой физической величины характеризует инерционные свойства тела, то есть способность некоторой силы изменять скорость тела, а также кинетическую энергию, которой оно обладает.
Гравитационная масса связана с интенсивностью притяжения между любыми телами. Она играет важную роль в космосе, поскольку благодаря притяжению между звездами и планетами существует наша галактика и наша Солнечная система. Однако гравитационная масса проявляет себя и в повседневной жизни в виде наличия у всех тел некоторого веса.
Формулы для инерции
В физике формула нахождения массы инерционной имеет следующий вид:
Помимо записанного выражения, следует привести еще одну формулу нахождения массы в физике, которая связана с явлением инерции. Эта формула имеет вид:
Формула для гравитации
Математическое описание явления гравитации стало возможным благодаря многочисленным наблюдениям за движением космических тел. Результаты всех этих наблюдений в XVII веке обобщил Исаак Ньютон в рамках закона всемирного тяготения. Согласно этому закону, два тела, которые имеют массы m1 и m2, друг к другу притягиваются с такой силой F:
Если в данное выражение подставить значение массы нашей планеты и ее радиус, тогда мы получим следующую формулу массы в физике:
Весы, которыми человек пользуется в быту (механические, электронные), показывают массу тела, однако измеряют его вес. Перевод между этими величинами является лишь вопросом калибровки прибора.
Плотность и объем
Объем представляет собой некоторую часть пространства, которая ограничена поверхностью тела. Измеряется он в кубических единицах длины, например, в м3.
Формула массы вещества через объем и плотность записывается так:
Чем больше объем тела и чем выше его плотность, тем большей массой оно обладает. В связи с этим фактом полезно вспомнить знаменитую загадку про то, что имеет большую массу: 1 тонна пуха или 1 тонна железа. В отсутствии выталкивающей архимедовой силы массы обоих веществ равны. Пух имеет гораздо меньшую плотность, чем железо, однако разница в плотности компенсируется аналогичной разницей в объеме.
Относительная
Понятие об относительной массе применяется в атомной физике и в химии. Поскольку массы атомов и молекул имеют очень маленькие значения (≈10-27 кг), то оперировать ими на практике при решении задач оказывается крайне неудобно. Поэтому сообществом ученых было решено использовать так называемую относительную массу, то есть рассматриваемая величина выражается в единицах массы по отношению к массе известного эталона. Этим эталоном стала 1/12 массы атома углерода, которая равна 1,66057*10-27 кг. Соответствующая относительная величина получила название атомной единицы (а. е. м.).
Формулу относительной массы M можно записать так:
M = 26,5606 * 10-27 / (1,66057 * 10-27) = 15,9949.
Поскольку а. е. м. является относительной величиной, то она не имеет размерности.
Удобство применения этого термина на практике заключается не только в небольших и целых значениях этой единицы измерения. Дело в том, что значение а. е. м. совпадает по величине с молярной массой, выраженной в граммах. Последняя представляет собой массу одного моль вещества.
Энергия
Выше были приведены разные формулы, как найти массу в физике. Завершая статью, хотелось бы отметить связь массы и энергии. Это связь носит фундаментальный характер, который отражает пространственно-временные свойства нашей Вселенной. Соответствующая формула массы в физике, полученная Альбертом Эйнштейном, имеет вид:
Квадрат скорости света c является коэффициентом перевода между массой и энергией. Это выражение говорит о том, что обе величины, по сути, являются одной и той же характеристикой материи.
Записанное выражение было подтверждено экспериментально при изучении ядерных реакций и реакций элементарных частиц.
Гравитационная масса
Ма́сса — одна из важнейших физических величин. Первоначально (XVII–XIX века) она характеризовала «количество вещества» в физическом объекте, от которого, по представлениям того времени, зависели как способность объекта сопротивляться приложенной силе (инертность), так и гравитационные свойства — вес. В современной физике понятие «количество вещества» имеет другой смысл, а под массой понимают два различных свойства физического объекта:
Теоретически, гравитационная и инертная масса равны, поэтому в большинстве случаев просто говорят о массе, не уточняя какую из них имеют в виду.
Масса тела не зависит от того, какие внешние силы и в какой момент на это тело действуют.
Содержание
Исследование единства понятия массы
Гравитационная масса — характеристика материальной точки при анализе в классической механике, которая полагается причиной гравитационного взаимодействия тел, в отличие от инертной массы, которая определяет динамические свойства тел.
Как установлено экспериментально, эти две массы пропорциональны друг другу. Не было обнаружено никаких отклонений от этого закона, поэтому новых единиц измерения для инерционной массы не вводят (используют единицы измерения гравитационной массы) и коэффициент пропорциональности считают равным единице, что позволяет говорить и о равенстве инертной и гравитационной масс.
Можно сказать, что первая проверка пропорциональности двух видов массы была выполнена Галилео Галилеем, который открыл универсальность свободного падения. Согласно опытам Галилея по наблюдению свободного падения тел, все тела, независимо от их массы и материала, падают с одинаковым ускорением свободного падения. Сейчас эти опыты можно трактовать так: увеличение силы, действующей на более массивное тело со стороны гравитационного поля Земли, полностью компенсируется увеличением его инертных свойств. Следовательно, гравитационная масса пропорциональна инертной массе [1]
На равенство инертной и гравитационной масс обратил внимание ещё Ньютон, он же впервые доказал, что они отличаются не более чем на 0,1 % (иначе говоря, равны с точностью до 10 −3 ).. На сегодняшний день это равенство экспериментально проверено с очень высокой степенью точности (3×10 −13 ).
Фактически, равенство гравитационной и инертной масс было сформулировано А. Эйнштейном в виде слабого принципа эквивалентности — составной части принципов эквивалентности, положенных в основу общей теории относительности. Существует также сильный принцип эквивалентности — по которому в свободно падающей системе локально выполняется специальная теория относительности. Он на сегодняшний день проверен со значительно меньшей точностью.
В классической механике — масса есть величина аддитивная (масса системы равна сумме масс составляющих её тел) и инвариантная относительно смены системы отсчёта. В релятивистской механике масса неаддитивная величина, но тоже инвариантная, и хотя здесь под массой понимается абсолютная величина 4-вектора энергии-импульса, лоренц-инвариантная.
Определение массы
В СТО масса тела m определяется из уравнения релятивистской динамики [3] :
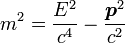
где E — полная энергия свободного тела, p — его импульс, c — скорость света.
Определённая выше масса является релятивистским инвариантом, то есть она одна и та же во всех системах отсчёта. Если перейти в систему отсчёта, где тело покоится, то 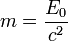
Следует однако отметить, что частицы с нулевой инвариантной массой (фотон, гравитон…) двигаются в вакууме со скоростью света (c ≈ 300000 км/сек) и поэтому не обладают системой отсчёта, в которой бы покоились.
Масса составных и нестабильных систем
Инвариантная масса элементарной частицы постоянна, и одинакова у всех частиц данного типа и их античастиц. Однако, масса массивных тел, составленных из нескольких элементарных частиц (например, ядра или атома) может зависеть от их внутреннего состояния.
Для системы, подверженной распаду (например, радиоактивному), величина энергии покоя определена лишь с точностью до постоянной Планка, делённой на время жизни: 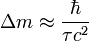
Единицы массы
В системе СИ масса измеряется в килограммах. В системе СГС используются граммы. Иногда используются также другие единицы измерения массы.
Инертная и гравитационная масса
ИНЕРТНАЯ И ГРАВИТАЦИОННАЯ МАССА
Кандидат технических наук
Из современного представления инертной массы следует, что это такая масса, которая согласно второму закону Ньютона, приобретает постоянное ускорение при приложении к ней постоянной силы.
А разве согласно первому закону Ньютона тело, движущееся по инерции равномерно и прямолинейно при отсутствии на него силового воздействия, не обладает инертной массой? И что – для его торможения не нужно прикладывать к нему силу?
Так вот как раз именно такую инертную массу и следует рассматривать при её сравнении с гравитационной массой.
При этом эти обе массы и гравитационную и инертную нужно поставить в идеальные условия, т. е. удалить от них другие массы, которые могут воздействовать на процесс сравнения, что выполнено ниже.
В классической механике Ньютона и в ТО Эйнштейна принято, что инертная масса тела равна своей гравитационной массе. Поэтому принято считать, что это распространяется на все случаи жизни.
Однако, что происходит в действительности – под большим вопросом.
Попробуем разобраться в этом вопросе исходя из наших предположений и последовавшими за этим выводами.
В нашей теоретической работе «Гравитонно-газовая модель тяготения» [1] мы предположили, что все тела поглощают гравитонный газ и все тела являются пространственными стоками. Графически это выглядит как сферически симметричное семейство линий тока гравитонов к центру сферы (к телу), причем частота линий характеризует величину массы тела, чем больше масса – тем чаще линии.
Гравитационная масса – это масса, находящаяся только в зоне действия массы – источника гравитации, которая, так же как и наша исследуемая масса, поглощает гравитонный газ, рис. 1.
Инертная масса – это масса, движущаяся по инерции (прямолинейно и равномерно согласно определению Ньютона) при бесконечном удалении от других масс. Здесь исходные линии тока гравитонов к этой нашей массе прямолинейны и движутся совместно с массой с той же скоростью. В толще покоящегося гравитонного газа скорость инертной массы, учитывая потенциальность движения, выглядит как равномерная частота параллельных линий, лежащих в направлении движения этой массы. Чем выше скорость – тем больше частота параллельных линий, рис. 2.
Частота исходных линий тока гравитонов к гравитационной массе и инертной массе приняты нами равными между собой. Это подразумевает исходное равенство этих масс.
Частота исходных линий встречного потока гравитонов и частота исходных линий тока гравитонов к массе – источнику гравитации (рис.1 и рис. 2) выбраны таким образом, что расстояния между исходными линиями на уровне нашей исследуемой массы были равны между собой.
Сделано это с той целью, чтобы поставить исследуемые массы в одинаковые условия и проанализировать, что происходит с гравитационными фронтами этих масс.
Из рисунков видно, что картинки практически идентичны, а именно: гравитационные фронты обеих масс загнуты вправо как для случая левого расположения
Стр.2из3
массы – источника гравитации у гравитационной массы (рис.1), так и при равномерном движении инертной массы влево (рис. 2).
Разница состоит в том, что у гравитационной массы (вследствие веерного расположения линий тока гравитонов у массы – источника гравитации) расстояние от полюса гравитационного фронта до центра гравитационной массы несколько меньше, чем это же расстояние у инертной массы (линии скорости – параллельны). При этом гравитационный фронт на периферии у гравитационной массы несколько шире, чем у инертной массы. Таким образом, даже при близких исходных условиях, гравитационные потоки в зонах расположения гравитационной и инертной масс ведут себя по-разному, и нельзя строго утверждать, что гравитационная и инертная массы равны между собой. Можно только говорить о некоторой их близости.
Необходимо отметить, что мы в рис.1 специально создали условия очень большого расстояния от массы – источника гравитации до гравитационной массы и исходные линии тока массы – источника гравитации сделали очень частыми (это соответствует пренебрежительно малой гравитационной массы по отношению к массе – источнику гравитации).
А в случае равенства нашей гравитационной массы и массы – источника гравитации гравитационный фронт вообще представляет собой плоскость, перпендикулярную линии соединения масс, чего никогда не может быть при движущейся по инерции массе (здесь гравитационный фронт может быть только загнутый в сторону, обратную направлению движения инертной массы).
Так, что говорить о равенстве гравитационной и инертной масс в этом, указанном случае, мягко говоря – слегка самонадеянно.
А что касается случая, когда наша гравитационная масса больше массы – источника гравитации, то здесь уже гравитационный фронт нашей массы становится вогнутым, т. е. загибается в сторону меньшей массы – источника гравитации, и говорить о равенстве нашей гравитационной массы нашей инертной массе в этом случае просто бессмысленно.
Таким образом, приходим к выводу: гравитационная и инертная массы не равны, а близки по величине только при определённых условиях, когда гравитационная масса пренебрежительно мала по отношению к массе – источнику гравитации и, одновременно, когда расстояние между гравитационной массой и массой – источником гравитации близко к бесконечности.
Масса тела в один килограмм, лежащего на поверхности Земли, может быть равна массе тела в один килограмм, лежащего на поверхности Луны, или вращающегося вокруг Земли как спутник. Его инертная масса близка к своей гравитационной массе, т. к. во всех трёх случаях это тело находится в одинаковых условиях.
— линии тока гравитонов к Земле и Луне у их поверхностей практически параллельны между собой вследствие распределённости масс Земли и Луны по своим объёмам, что соответствует условию расстояния от массы – источника гравитации до исследуемой массы близкого к бесконечности или параллельности линий скорости у инертной массы по рис. 2.
— масса этого тела пренебрежительно мала по сравнению с массами Земли и Луны.
Гравитационная и инертная массы не равны между собой, а близки и то при одинаковых условиях.
[1] www. vitia-kuzovkov. *****/gazovaya_model_tiagotenia. doc
Сила тяжести, масса и вес тела, невесомость
Масса
Масса обозначается символом \(m \), является скалярной величиной и в СИ измеряется в килограммах.
Иногда массу в условии некоторых задач задают в граммах или, например, в тоннах. Чтобы перевести массу в килограммы, используют такие формулы:
\[ \large \boxed < \begin
От массы зависят инерционные и гравитационные свойства физических тел.
Масса в природе проявляет себя двумя способами. Поэтому, выделяют:
Инертная масса
Масса инертная влияет на способность тела двигаться по инерции. Такая масса используется в формуле второго закона Ньютона.
Пусть два тела находятся в инерциальной системе отсчета. Если какая-либо сила одинаково ускоряет эти тела, то они обладают одинаковой инертной массой. Здесь «одинаково ускоряет» следует понимать, как «сообщает одинаковые ускорения».
Гравитационная масса
Гравитационная масса определяет силу, с которой тело притягивается к другим телам. Эта масса используется в формуле закона всемирного тяготения.
Различные эксперименты показали, что инертная и гравитационная массы равны с высокой степенью точности. Поэтому, при изучении школьной физики можно просто говорить «масса», не уточняя, о какой именно массе идет речь.
Так же, масса входит в формулы для расчета импульса и механической энергии.
Массой обладают все макроскопические тела, а, так же, такие элементарные частицы, как протоны, нейтроны, электроны и т. д. Однако, существуют и частицы, у которых нет массы покоя, например – фотоны.
Примечание: Фотон – элементарная частица, переносчик электромагнитного взаимодействия, движется со скоростью света, часто проявляет волновые свойства. Подробнее о фотонах вы узнаете в основах квантовой физики.
Сила тяжести
Сила тяжести — это сила, с которой Земля притягивает к себе тело.
\(\large \vec
\(\large m \left(\text<кг>\right) \) — масса тела;
Вес – это сила. Этой силой тело давит на опору, когда опирается на нее, или растягивает подвес, когда на нем висит.
Является векторной величиной и обозначается символом \(\vec
\).
\(\vec
\left(H\right) \) – вес тела, как любая сила в СИ измеряется в Ньютонах.
Вес отличается от массы. Вес, как и любая сила, измеряется в Ньютонах, а масса измеряется в килограммах.
Когда тело опирается о горизонтальную поверхность, его вес равен по модулю силе реакции опоры по третьему закону Ньютона. Поэтому, в задачах для нахождения веса удобно вычислять силу \(\large \vec
Примечание: Векторы равны по модулю, когда обладают одинаковыми длинами. Так как длина вектора обозначается числом, то физики о равных по модулю векторах сил могут сказать: силы численно равны.
Чем вес отличается от силы тяжести
Вес — это сила, принадлежащая телу. А сила тяжести — это сила, действующая на тело со стороны планеты, или любого другого (крупного) тела.
Что такое невесомость
Подбросим мяч вверх и рассмотрим свободный полет мяча. Пока он в полете, он не давит на опору и не растягивает подвес. Проще говоря, мяч находится в невесомости – то есть, не имеет веса.
Масса есть всегда, а вес может отсутствовать! Как убедимся чуть позже, одна и та же масса может обладать различным весом.
Как изменяется вес тела лифте
Давайте выясним, какой вес имеет тело, находящееся в покоящемся лифте, или в лифте, который будет двигаться вверх или вниз с ускорением, или без него.
Если скорость лифта не изменяется
Сначала рассмотрим покоящийся лифт (рис. 1а), либо движущийся вверх (рис. 1б), или вниз (рис. 1в) с неизменной скоростью.
Примечание: «неизменной», также, значит «постоянной», или «одной и той же».
По первому закону Ньютона, когда действие других тел скомпенсировано, тело, не меняющее свою скорость, находится в инерциальной системе отсчета.
Как видно из рисунка, взаимодействуют два объекта: тело и опора. Тело давит своим весом на опору, а опора отвечает телу (рис. 1) силой своей реакции.
Будем записывать для рассмотренных случаев рисунка 1 векторные силовые уравнения:
\[ \large N – m \cdot g = 0 \]
А в этой статье подробно и с объяснениями написано о том, как составлять силовые уравнения (ссылка).
Прибавив к обеим частям уравнения величину \( m \cdot \vec
По третьему закону Ньютона, вес тела и реакция опоры направлены противоположно и равны по модулю. Поэтому, найдя силу реакции опоры, мы автоматически находим вес тела.
Воспользуемся тем, что \( \left|\vec \right|\), получим То есть, вес тела в покоящемся лифте, или движущемся вверх или вниз с неизменной скоростью, будет равен \( mg \). Если вектор скорости лифта не изменяется ни по направлению, ни по модулю, лифт можно считать инерциальной системой отсчета. Теперь выясним, каким весом будет обладать тело в лифте, движущемся с ускорением (рис. 2). Примечание: Лифт, движущийся с ускорением, не является инерциальной системой отсчета. Читайте подробнее о инерциальных системах. Запишем силовые уравнения. Для рисунка 2а, уравнение выглядит так: \[ \large N – m \cdot g = m \cdot a \] А для рисунка 2б, так: \[ \large N – m \cdot g = — m \cdot a \] Прибавим теперь к обеим частям уравнений величину \( m \cdot g \), получим: \( \large N = m \cdot a + m \cdot g \) – для случая рис. 2а; \( \large N = — m \cdot a + m \cdot g \) – для рис. 2б; Вынесем массу за скобки \( \large N = m \cdot \left( a + g \right) \) – для рис. 2а; Учтем, что \( \left|\vec \right|\), окончательно запишем Для рисунка 2а — движение лифта вверх с ускорением: Вес тела в движущемся с ускорением вверх лифте, будет равен \( m \cdot \left( g + a \right) \), то есть, превышает величину \( m \cdot g \). Когда лифт движется вниз с ускорением (рис. 2б), вес тела, наоборот — уменьшается: Напомним, что вес в покоящемся, или движущемся вверх или вниз с неизменной скоростью лифте, в точности равен \( m \cdot g \). Вес тела в движущемся вниз с ускорением лифте, равен \( m \cdot \left( g — a \right) \), это меньше величины \( m \cdot g \). Значит, одна и та же масса может обладать разным весом, мало того, в некоторых случаях вес вообще может отсутствовать. Масса есть всегда, а вес может отсутствовать! Когда вес тела больше силы тяжести, говорят, что возникает перегрузка. \[ \large \boxed < P >m \cdot g >\] Когда говорят о перегрузке, принято сравнивать ускорение движения вверх с ускорением свободного падения \(\large \vec Например, при движении ракеты с ускорением вверх, космонавт может испытывать перегрузки до 7g. Это значит, что его вес увеличивается в 7 раз. Первый космонавт мира — Юрий Гагарин, упоминал о перегрузке: «…какая-то сила вдавливает меня в кресло все больше и больше. … трудно пошевелить рукой или ногой…». Подобным образом мы испытываем перегрузки в самолете во время взлета — эти перегрузки вдавливают нас в кресло. Правда, эти перегрузки значительно меньше, чем перегрузки летчиков — спортсменов, или военных, летчиков — космонавтов. Представители этих профессий тренируют свое тело для того, чтобы перегрузки легче переносить. \(P = m \cdot g \) — вес тела в покоящемся или движущемся вверх или вниз с постоянной скоростью лифте. \( P = m \cdot \left( g + a \right) \) — вес, когда лифт движется с ускорением вверх; \( P = m \cdot \left( g — a \right) \) — вес в движущемся вниз с ускорением; Если ускорение лифта при его движении вниз \( a = g \), наступит невесомость, вес тела исчезнет \( P = 0 \).Если скорость лифта изменяется
Что такое перегрузка
Подведем итоги