что такое граница треугольника

Треугольник

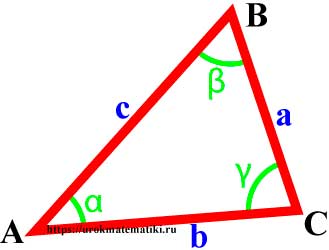
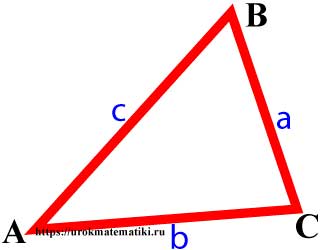
Треугольник произвольный

Треугольник – это многоугольник с тремя сторонами (тремя углами).

Виды треугольников :+ показать

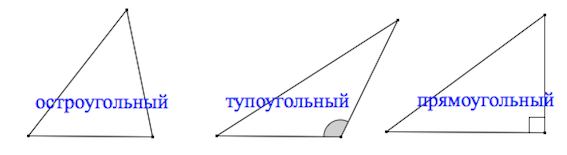
Остроугольный треугольник – треугольник, у которого все углы острые (то есть меньше 90˚).

Тупоугольный треугольник – треугольник, у которого один из углов тупой (больше 90˚).

Прямоугольный треугольник – треугольник, у которого один из углов прямой (равен 90˚).

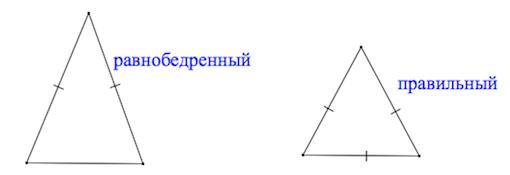
Равносторонний (правильный) треугольник – треугольник, у которого все три стороны равны.

Свойства

1. Против большей стороны лежит больший угол, и наоборот.

2. Против равных сторон лежат равные углы, и наоборот.

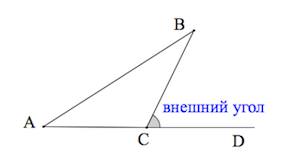
4. Внешний угол треугольника равен сумме внутренних углов,
не смежных с ним:

(Внешний угол образуется в результате продолжения одной из сторон треугольника).

5. Любая сторона треугольника меньше суммы двух других сторон.

Признаки равенства треугольников

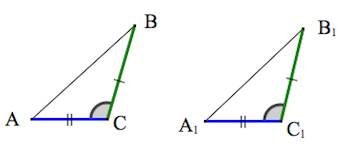
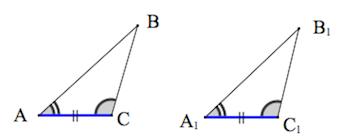
1. Треугольники равны, если у них соответственно равны две стороны и угол между ними.

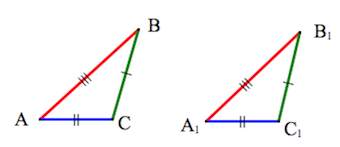
3. Треугольники равны, если у них соответственно равны три стороны.

Биссектриса, высота, медиана

Здесь подробно о биссектрисе, высоте, медиане треугольника.

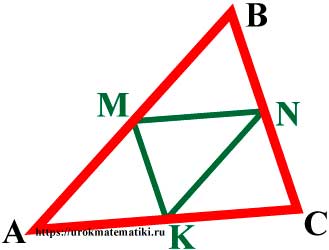
Средняя линия треугольника

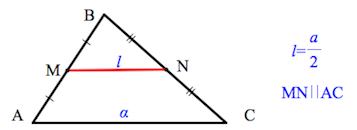
Средняя линия треугольника – отрезок, соединяющий середины двух сторон треугольника.

Средняя линия треугольника параллельна третьей стороне и равна ее половине.

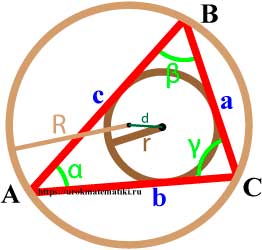
Вписанная окружность

Центр вписанной окружности – точка пересечения биссектрис треугольника.

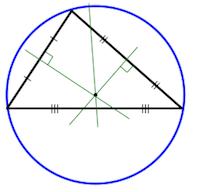
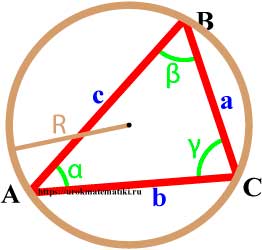
Описанная окружность

Центр описанной окружности – точка пересечения серединных перпендикуляров.

Соотношение сторон в произвольном треугольнике

Теорема косинусов:

Теорема синусов:

Площадь треугольника

Через сторону и высоту

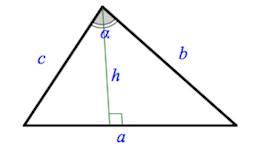
Через две стороны и угол между ними

Через радиус описанной окружности

Через радиус вписанной окружности

, где – полупериметр

, где – полупериметр

Смотрите также площадь треугольника здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Есть пара ошибок в формулах. В частности в формуле вычисления площади через 2 стороны и угол между ними, в теореме Синусов, в разделе “свойства”.
А вообще отличные статьи, очень выручают, всё понятно и доступно, премного благодарен 😉

Анатолий, спасибо!
В разделе “свойства” ошибок не нашла…
В теореме синусов, – да… не пропечаталась буква гамма. Подправила.
В формуле площади треугольника, вы правы – картинка не соответствовала формуле. Исправила.
К сожалению, ошибки сразу не всегда замечаются.
Благодарю еще раз!

В разделе свойства:

Да, не хватало значка «» у А. Спасибо! 😉

Здраствуйте! Мне нужна ваша помощь!
Задача: ВЕРШИНЫ ТРЕУГОЛЬНИКА ДЕЛЯТ ОПИСАННУЮ ОКОЛО НЕГО ОКРУЖНОСТЬ НА ТРИ ДУГИ, ДЛИНЫ КОТОРЫХ ОТНОСЯТСЯ КАК 6:7:33. НАЙДИТЕ РАДИУС ОКРУЖНОСТИ, ЕСЛИ МЕНЬШАЯ ИЗ СТОРОН РАВНА 11.

Подозреваю, у вас опечатка в условии…
Если длины дуг (а значит и их градусные меры) находятся в отношении , то выходим на уравнение Откуда Значит угол треугольника, что напротив меньшей стороны, есть
Применяем теорему синусов: , откуда

спасибо я так и думал а то не могу решить и всё
СПАСИБО!

Здравствуйте. Пожалуйста, объясните, как решить задачу:
Вписанная в теругольник ABC окружность касается сторон AB, BC и AC в точках K,L и М соответственно.Найдите KL, если AM=2, МС=3 и угол С=π/3

Очевидно,
Примите за .
Примените к треугольнику теорему косинусов:

Найдете , далее можно найти угол и из треугольника найти

Спасибо большое за ваш сайт. Очень радует, тот факт, что когда люди не понимают какую-нибудь задачу, вы помогаете решить. Спасибо. Побольше бы таких сайтов, всё понятно и доступно

Источник

Пространство треугольников (окончание)

Алексей Панов, Дмитрий Ал. Панов, Пётр Панов
«Квантик» №3, 2021

Начало в «Квантике» № 1 и № 2, 2021.

Точка, где небо касается Земли, — исследователь на границе Мира. «Гравюра Фламмариона», Википедия

А теперь двинемся к границам и полюсам Треугольного Мира. При этом постоянно будем следить за треугольниками, мимо которых проходим.

Равнобедренные треугольники

Рис. 11. Равнобедренный треугольник

Особое место в Треугольном Мире занимают равнобедренные треугольники, нанизанные на его экваторы как позвонки (рис. 12).

Определение. Равнобедренный треугольник — это треугольник с двумя равными сторонами (рис. 11).

Теорема. В равнобедренном треугольнике против равных сторон лежат равные углы. Если в треугольнике два угла равны, то против них лежат равные стороны и треугольник равнобедренный.

В направлении границы

Что происходит с нарисованными на карте треугольниками по мере приближения к границе (движение вдоль первой стрелки на рисунке 12)?

Рис. 12. На карте проложен маршрут: сначала мы движемся к границе Мира, а потом вдоль неё к Красному полюсу

Ответ очевиден: они сплющиваются и на самой границе превращаются в отрезок с отмеченной на нём точкой — в сплюснутый треугольник (рис. 13).

Рис. 13. Сплюснутый треугольник, a = b + c

Для сплюснутого треугольника неравенство треугольника превращается в равенство. В нём большая сторона равна сумме двух других: a = b + c.

Упражнение 12. Чему равны углы сплюснутого треугольника на рисунке 13?

Углы равны, равны ли стороны?

С теоремой о равнобедренном треугольнике на границе Треугольного Мира нас ждёт сюрприз. Наверное, вы догадались, что у сплюснутого треугольника на рисунке 13 один угол (зелёный) равен 180°, а остальные два — по 0°. Но против этих двух равных нулевых углов лежат две неравные стороны b ≠ c.

Выходит, вторая часть теоремы неверна? К счастью, математики давно разработали нужную теорию — анализ бесконечно малых. На нашем маршруте мы шли мимо треугольников, у которых можно отметить свои синий и красный углы. При подходе к границе и синие, и красные углы постепенно «превращаются» в нулевые, но делают это не одинаково. Вычислив в каждом треугольнике отношение синего угла к красному, мы увидим: пока эти углы ещё не стали нулями, но уже практически «бесконечно малы», их отношение не отличить от b/c. С этой точки зрения, условно будем считать, что в сплюснутом треугольнике синий и красный углы относятся друг к другу как b/c.

Так бесконечно малые спасают теорему о равнобедренном треугольнике: нулевые углы (рис. 13) не равны друг другу с точки зрения их отношения! Они будут равными лишь для равнобедренного сплюснутого треугольника, где \( a = \frac<1> <2>\), \( b = \frac<1> <4>\), \( c = \frac<1> <4>\).

Упражнение 13. Где расположен этот треугольник на карте (это недалеко от места нашего выхода на границу)?

Но продолжим наш маршрут.

К полюсу вдоль границы

По мере приближения к Красному полюсу (вдоль второй стрелки) длины сторон a и b выравниваются, сторона c уменьшается, а две вершины сплюснутого треугольника (зелёная и синяя) сближаются (рис. 12). В итоге полюс предстаёт перед нами равнобедренным треугольником со сторонами \( a = \frac<1> <2>\), \( b = \frac<1> <2>\), c = 0.

Рис. 14. Треугольник, представляющий Красный полюс

Угол между a и b равен 0°. А два других угла?

Тайна красного полюса

Мы зашли в Красный полюс вдоль границы Треугольного Мира. Все треугольники, мимо которых мы проходили, были сплюснутыми и все имели углы 0°, 180° и 0°. Менялись только длины их сторон. С этой точки зрения углы полюсного сплюснутого треугольника (рис. 14) тоже должны быть 180°, 0° и 0°.

Рис. 15. Треугольники вблизи Красного полюса, вершины окрашены в цвет того полюса, на который они указывают

Но если входить в Красный полюс вдоль экватора, то у полюсного треугольника стороны будут те же самые \( \frac<1> <2>\), \( \frac<1> <2>\), 0, а вот углы будут 90°, 90° и 0°. Тот же треугольник с углами 90°, 90° и 0° мы получим, входя в полюс вдоль меридиана, соответствующего 90°.

И вообще, входя вдоль меридиана, отвечающего углу α°, мы увидим на полюсе треугольник со сторонами \( \frac<1> <2>\), \( \frac<1> <2>\), 0 и углами α°, 180° − α°, 0°. Значит, мы не можем приписать двум нашим углам какие-то определённые значения, а получаем на Красном полюсе целое семейство сплюснутых треугольников (рис. 15). И то же самое — на остальных полюсах.

На полюсе: стороны равны, углы нет

Итак, Красный полюс вмещает целое семейство треугольников с равными сторонами \( a = b = \frac<1> <2>\), углы против которых не равны между собой. И неверна первая часть теоремы о равнобедренном треугольнике.

В этот раз мы спасём теорему, применив другой математический трюк: превратим её в определение.

Определение. Треугольник — равнобедренный, если в нём есть две равные стороны и два равных угла, причём равные углы лежат против равных сторон, а равные стороны — против равных углов.

Замечание. Среди сплюснутых треугольников есть два типа равнобедренных — с двумя углами 0° и с двумя углами 90°. Равнобедренные треугольники второго типа расположены в полюсах Треугольного Мира.

Упражнение 14. С помощью нашего нового Определения равнобедренного треугольника докажите ранее сформулированную Теорему о равнобедренном треугольнике.

Наше путешествие завершено, но история Треугольного Мира на этом не заканчивается.

Послесловие: треугольный мир II

Треугольный Мир возник благодаря нескольким измерениям внутри правильного треугольника.

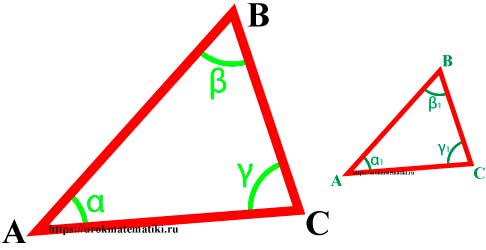
Предлагаем вам провести новую серию измерений. Нарисуйте любой треугольник. Измерьте транспортиром его углы α, β, γ и вычислите их сумму α + β + γ. Сделайте пять экспериментов, рисуя каждый раз новый треугольник, и заполните журнал измерений. Вы получите удивительный результат! Попробуйте на его основе построить новый Треугольный Мир II.

Источник

Треугольник

Треугольник — фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.

Типы треугольников

По величине углов

Остроугольный треугольник

— все углы треугольника острые.

Тупоугольный треугольник

— один из углов треугольника тупой (больше 90°).

Прямоугольный треугольник

— один из углов треугольника прямой (равен 90°).

По числу равных сторон

Разносторонний треугольник

— все три стороны не равны.

Равнобедренный треугольник

Равносторонний (правильный) треугольник

— все три стороны равны.

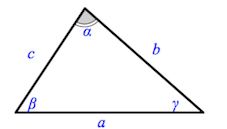
Вершины, углы и стороны треугольника

Свойства углов и сторон треугольника

Сумма углов треугольника равна 180°

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов.

a sin α = b sin β = c sin γ

Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведение этих сторон на косинус угла между ними.

Теорема о проекциях

Для остроугольного треугольника:

a = b cos γ + c cos β
b = a cos γ + c cos α;
c = a cos β + b cos α;

Формулы для вычисления длин сторон треугольника

Формулы сторон через медианы

Медианы треугольника

Медиана треугольника — отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.

Свойства медиан треугольника

S ∆AOF = S ∆AOE = S ∆BOF = S ∆BOD = S ∆COD = S ∆COE

Формулы медиан треугольника

Формулы медиан треугольника через стороны

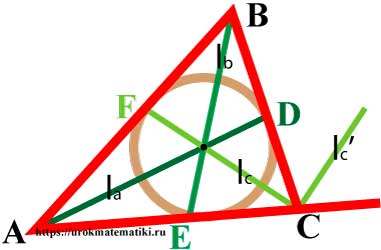
Биссектрисы треугольника

Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.

Свойства биссектрис треугольника

Угол между l c и l c ‘ = 90°

Формулы биссектрис треугольника

Формулы биссектрис треугольника через стороны

где p = a + b + c 2 — полупериметр треугольника.

Формулы биссектрис треугольника через две стороны и угол

l a = 2 b c cos α 2 b + c

l b = 2 a c cos β 2 a + c

l c = 2 a b cos γ 2 a + b

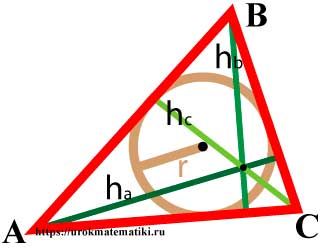
Высоты треугольника

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.

В зависимости от типа треугольника высота может содержаться:

Свойства высот треугольника

Формулы высот треугольника

Формулы высот треугольника через сторону и угол

h a = b sin γ = c sin β

h b = c sin α = a sin γ

h c = a sin β = b sin α

Формулы высот треугольника через сторону и площадь

Формулы высот треугольника через две стороны и радиус описанной окружности

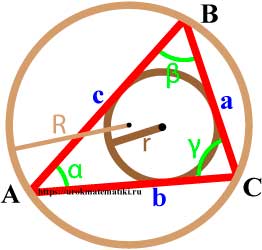
Окружность вписанная в треугольник

Окружность называется вписанной в треугольник, если она касается всех трех его сторон.

Свойства окружности вписанной в треугольник

Формулы радиуса окружности вписанной в треугольник

Радиус вписанной в треугольник окружности равен отношению площади треугольника к его полупериметру

Радиус вписанной в треугольник окружности через три стороны

Формулы высот треугольника через две стороны и радиус описанной окружности

Окружность описанная вокруг треугольника

Окружность называется описанной вокруг треугольника, если она содержит все вершины треугльника.

Свойства окружности описанной вокруг треугольника

Свойства углов

Центр описанной окружности лежит внутри остроугольного треугольника, снаружи тупоугольнго треугольника, на середине гипотенузы прямоугольного треугольника.

Формулы радиуса окружности описанной вокруг треугольника

Радиус описанной окружности через три стороны и площадь

Радиус описанной окружности через площадь и три угла

Радиус описанной окружности через сторону и противоположный угол (теорема синусов)

Связь между вписанной и описанной окружностями треугольника

Формулы радиуса окружности описанной вокруг треугольника

Если d — расстояние между центрами вписанной и описанной окружностей, то

Радиус описанной окружности через площадь и три угла

Средняя линия треугольника

Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.

Свойства средней линии треугольника

Признаки

Если отрезок параллелен одной из сторон треугольника и соединяет середину стороны треугольника с точкой, лежащей на другой стороне треугольника, то этот отрезок — средняя линия.

Периметр треугольника

Периметр треугольника ∆ABC равен сумме длин его сторон.

Формулы площади треугольника

Формула площади треугольника по стороне и высоте

Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.

где a, b, c — стороны треугольника,
h_a, h_b, h_c — высоты, проведенные к сторонам a, b, c треугольника.

Формула площади треугольника по трем сторонам

где p — полупериметр треугольника: p = a + b + c 2
a, b, c — стороны треугольника.

Формула площади треугольника по двум сторонам и углу между ними

Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

Формула площади треугольника по трем сторонам и радиусу описанной окружности

Формула площади треугольника по трем сторонам и радиусу вписанной окружности

Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

Равенство треугольников

Определение

Если два треугольника АВС и А₁В₁С₁ можно совместить наложением, то они равны.

Свойства

У равных треугольников равны и их соответствующие элементы. (В равных треугольниках против равных сторон лежат равные углы, против равных углов лежат равные стороны).

Признаки равенства треугольников

По двум сторонам и углу между ними

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

По стороне и двум прилежащим углам

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

По трем сторонам

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Подобие треугольников

Определение

Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.

где k — коэффициент подобия.

Признаки подобия треугольников

Свойства

Площади подобных треугольников относятся как квадрат коэффициента подобия:

Прямоугольные треугольники

Прямоугольный треугольник — треугольник, в котором один угол прямой (то есть равен 90˚).

Свойства прямоугольного треугольника

Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы (гипотенуза в два раза длиннее катета, лежащего против угла в 30°).

Рассмотрим прямоугольный треугольник ABC, в котором ∡A — прямой, ∡B = 30°, и значит, что ∡C = 60°.

Справедливо и обратное суждение: Если катет прямоугольного треугольника равен половине гипотенузы (или гипотенуза в два раза длиннее катета), то угол, лежащий против этого катета, равен 30°.

Признаки равенства прямоугольных треугольников

Так как в прямоугольном треугольнике угол между двумя катетами — прямой, а любые два прямых угла равны, то из общих признаков равенства треугольников для прямоугольных треугольников можно сформулировать свои признаки равенства.

Свойства

Площади подобных треугольников относятся как квадрат коэффициента подобия:

Источник