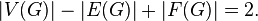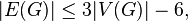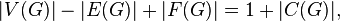что такое грань в графе

Теория Графов. Часть 1 Введение и классификация графов

«Графы являются одним из объединяющих понятий информатики – абстрактное представление, которое описывает организацию транспортных систем, взаимодействие между людьми и телекоммуникационные сети. То, что с помощью одного формального представления можно смоделировать так много различных структур, является источником огромной силы для образованного программиста». Стивен С. Скиена

Введение

Сначала под землей города Москвы ничего не было. Потом была построена первая станция метро, а затем и вторая и третья. Образовалось множество станций метро. На карту было занесено множество точек. Позже между станциями стали прокладывать пути линии. И соединилась станция метро А со станцией метро Б. Все остальные станции также стали соединятся друг с другом и на карте появилось множество линий. В итоге мы имеем Московский метрополитен очень красивый, я там был проверял.

Схема Московского метро

Посмотрите какая красота. У нас имеется множество точек (которые называются вершинами или узлами), а также множество линий (называемые рёбрами или дугами). Обозначим множество вершин буквой V от английского vertex−вершина и множество рёбер обозначим E от английского edge−ребро. Граф в формулах именуют буквой G. Все вершины обязательно должны быть идентифицированы.

Отмечу, что число вершин обозначается буквой n:

Число рёбер обозначается буквой m:

Таким образом граф задается и обозначается парой V,E:

Также определение графа рассказывается в этой статье на Хабре (https://habr.com/ru/post/65367/)

Неформально граф является совокупностью точек и линий. Линии в котором задаются парой вершин, расположенных не важно в каком порядке.

Разберем определение графа подробней. Может ли в G быть пустым множество E? Да без проблем! Такой граф будет называться нулевым, а вершины в нем будут называться изолированными.

Нулевой граф

Только вот множество V вершины пустым быть не может. Ведь множество E рёбра задается парой неупорядоченных вершин множества V. Две вершины образующие ребро, называются концами этого ребра.

Множество E задается парой неупорядоченных вершин множества V.

Пример: Пусть множество V = <1,2,3,4,5>. Тогда множество E =

Граф будет выглядеть следующим образом:

Висячей вершиной называется вершина которая соединена только с одной соседней вершиной. В нашем случаи висячей вершиной будет вершина 5, так как она соединена только с вершиной 1.

Степень записывают, как:

Максимальная степень, то есть какое количество степеней вообще присутствуют в графе обозначаются, как:

Формула суммы степеней для G = V,E выглядит так:

То есть сумма степеней всех вершин v графа равна удвоенному количеству его рёбер E. Считаем количество степеней в нашем примере. От этого никуда не денешься. Я насчитал 12. А теперь считаем, сколько у нас рёбер. Их 6! Умножаем на 2 и получаем 12. Совпадение? Не думаю!

А давайте представим наш граф в другом виде, но с сохранением данных пар. G теперь имеет следующий вид:

Заметьте я не изменил пары между собой. Вершина 4 также соединяется с вершиной 3, а у вершины 1 степень также осталась 4. Так почему граф имеет совершенно другой вид и законно ли это?

Классификации графов

Первым признаком классификации является отсутствие или наличие ориентации у ребер.

Ребро является неориентированным если у него нет понятия начала или конца. То есть оба его конца равноправны. Такой граф называется неориентированным, обыкновенным или неографом.

Неориентированный граф

Ориентированное ребро обозначается стрелкой. И указывает ориентацию от вершины к вершине. То есть данный граф имеет начало и конец. И называется он ориентированным или орграфом.

Ориентированный граф

Также существует граф со смешанными ребрами. Это когда в графе присутствуют, как ориентированные рёбра, так и неориентированные.

Смешанный граф

Вторым признаком является отсутствие или наличие кратных ребер.

Мультиграф

Граф в котором кратных ребер нет, является простым графом. В простом графе мы просто называем пару вершин для идентификации ребра, но в мультиграфе такое уже не сработает, так как одна и та же пара вершин будет указывать на два ребра и не понятно что к чему будет относится. Поэтому если вы повстречаете мультиграф, то вы должны обозначить каждое ребро отдельно.

Заключение

В данной стать я не рассмотрел, понятия смежности и инцидентности, однако я решил их рассмотреть в следующий раз. Также хочу отметить, что более подробно виды графов, я буду рассматривать в следующих статьях. Если у вас есть вопросы, предложения или я где-то допустил ошибки, то прошу написать их в комментариях.

Источник

Грань (теория графов)

Плана́рный граф — граф, который можно изобразить на плоскости без пересечений рёбер не по вершинам. Какое-либо конкретное изображение планарного графа на плоскости без пересечения рёбер не по вершинам называется плоским графом. Иначе говоря, планарный граф изоморфен некоторому плоскому графу, изображённому на плоскости так, что его вершины — это точки плоскости, а рёбра — кривые на плоскости, которые если и пересекаются между собой, то только по вершинам. Области, на которые граф разбивает плоскость, называются его гранями. Неограниченная часть плоскости — тоже грань, называемая внешней гранью. Любой плоский граф может быть спрямлён, то есть перерисован на плоскости так, что все его рёбра будут отрезками прямых.

Содержание

Свойства

Формула Эйлера

Оно было найдено Эйлером в 1736 г. [1] при изучении свойств выпуклых многогранников. Это соотношение справедливо и для других поверхностей с точностью до коэффициента, называемого эйлеровой характеристикой. Это инвариант поверхности, для плоскости или сферы он равен двум, а, например, для поверхности тора — нулю.

Формула имеет множество полезных следствий. Во-первых, все плоские укладки одного графа имеют одинаковое количество граней. Во-вторых, если каждая грань ограничена не менее чем тремя рёбрами (при условии, что в графе больше двух рёбер), а каждое ребро разделяет две грани, то

то есть при большем числе рёбер такой граф заведомо непланарен. Обратное утверждение неверно: в качестве контрпримера можно взять граф Петерсена. Отсюда следует, что в планарном графе всегда можно найти вершину степени не более 5.

Общая формула также легко обобщается на случай несвязного графа:

Два примера непланарных графов

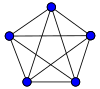
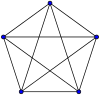
Полный граф с пятью вершинами

Лемма. Полный граф с пятью вершинами (К₅) нельзя уложить на плоскость.

«Домики и колодцы»

Задача о трёх колодцах. Есть три дома и три колодца. Можно ли так проложить дорожки между домами и колодцами, чтобы от каждого дома к каждому колодцу вела дорожка, и никакие две дорожки не пересекались бы. Мосты строить нельзя.

Лемма. Полный двудольный граф с тремя вершинами в каждой из долей (К_3,3) нельзя уложить на плоскость.

Доказательство. По формуле Эйлера граф имеет 5 граней.

Теорема Понтрягина — Куратовского

Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных полному графу из пяти вершин (K₅) или графу «домики и колодцы» (K_3,3).

Теорему также можно сформулировать в следующем варианте (иногда его называют «теорема Вагнера»).

Граф планарен тогда и только тогда, когда не содержит подграфов, стягивающихся в K₅ или K_3,3.

Компьютерная проверка на планарность

Признаки непланарных графов

Планарные графы в задачах

Раскраска карты. Необходимо раскрасить плоскую карту заданным числом красок так, что любые две страны, имеющие общий участок границы, имели различные цвета. Оказывается, что при отсутствии анклавов, всегда достаточно четырёх красок, но это утверждение чрезвычайно сложно доказать, см. Проблема четырёх красок.

Спрямление графа (теорема Фари). Любой плоский граф можно перерисовать так, чтобы он остался плоским, а рёбра стали отрезками прямых.

Обобщения

Граф укладывается на некоторой поверхности, если его можно на ней нарисовать без пересечения рёбер. Уложенный граф называется геометрическим, его вершины — это точки поверхности, а рёбра — линии на ней. Области, на которые граф разбивает поверхность, называются гранями. Плоский граф — граф, уложенный на плоскость.

Тороидальный граф — граф, который можно уложить на тор.

Источник

Грани плоского графа. Формула Эйлера

Гранью плоского графа называется максимальное по включению множество точек плоскости, каждая пара ко­торых может быть соединена жордановой кривой, не пересекающей ребра графа. Тем самым каждая точка плоскости принадлежит хотя бы одной грани плоского

графа. Границей грани будем считать множество вершин и ребер, принадлежащих этой грани.

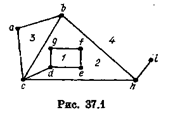
На рис. 37.1 изображен граф с четырьмя гранями. От­метим, что всякий плоский граф имеет одну, и притом единственную, неограниченную грань (на рис. 37.1 грань 4).

Такая грань называется внешней, а остальные грани — внутренними.

Легко видеть, что всякую внутреннюю грань плоско­го графа G можно

преобразовать во внешнюю с помощью стереографической проекции.

Для этого, воспользовав­шись теоремой 36.1, уложим граф G на сфере так,

чтобы северный полюс оказался внутри выбранной грани. Далее рассмотрим стереографическую проекцию G’ графа G на плоскость, касающуюся сферы в южном полюсе, т. е. в точке, диаметрально противоположной северному полюсу. Очевидно, что выбранная грань графа G станет при этом внешней в G’, а внешняя грань графа G — внутренней гранью графа G’, который изоморфен графу G. На рис. 37.2 представлен граф, получающийся из графа, изо­браженного на рис. 37.1, путем такого преобразования. При этом внутренняя грань 1 стала внешней.

Понятие грани естественным образом распространя­ется на псевдо- и мультиграфы (рис. 37.3).

Сформулируем несколько очевидных свойств плоских укладок графа, которые в дальнейшем будем неоднократ­но использовать, порой и не ссылаясь на них.

Свойство 1. Всякий планарный граф допускает такую плоскую укладку, в которой любая выбранная вершина (ребро) графа будет принадлежать внешней грани.

Свойство 2. Пусть граф G состоит из двух связ­ных компонент G₁ и G₂, являющихся плоскими графами,

и произвольным образом выбраны вершины v₁ Î VG₁ и v₂ Î VG₂. Тогда граф G₀, полученный из G слиянием вер­шин v₁ и v₂в вершину v, имеет плоскую укладку. При этом вершина v является точкой сочленения графа G? (рис. 37.4).

Аналогично можно «склеивать» два плоских графа и по ребру.

Свойство 3. Всякие две вершины, принадлежащие границе некоторой грани плоского графа, можно соеди-

нить простой цепью произвольной длины так, что вы­бранная грань разобьется на две грани.

Отметим, что это свойство является следствием известной теоремы Жордана о кривой.

Свойство 4. Для любого плоского графа каждая точка плоскости, не лежащая на ребре, входит только в одну грань, а каждая точка ребра, не являющаяся вершиной, входит только в одну грань, если это ребро яв­ляется мостом, и точно в две грани, если оно не мост.

Далее будем пользоваться следующими обозначениями: n, m, f—соответственно число вершин, ребер и гра­ней плоского графа.

21. Свойства планарных графов

Простейшие свойства плоских графов

Для связного плоского графа справедливо следующее соотношение между количеством вершин , ребер и граней (включая внешнюю грань):

Оно было найдено Эйлером в 1736 г. [1] при изучении свойств выпуклых многогранников. Это соотношение справедливо и для других поверхностей с точностью до коэффициента, называемого эйлеровой характеристикой. Это инвариант поверхности, для плоскости или сферы он равен двум, а, например, для тора — нулю.

Формула имеет множество полезных следствий. Во-первых, все плоские укладки одного графа имеют одинаковое количество граней. Во-вторых, если каждая грань ограничена не менее чем тремя рёбрами (при условии, что в графе больше двух ребер), а каждое ребро разделяет две грани, то

то есть, при большем числе рёбер такой граф заведомо непланарен. Обратное утверждение не верно: в качестве контрпримера можно взять граф Петерсена. Отсюда следует, что в планарном графе всегда можно найти вершину степени не более 5.

Общая формула также легко обобщается на случай несвязного графа:

где 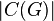— количество компонент связности в графе.

Два примера непланарных графов

Полный граф с пятью вершинами

K₅, полный граф с 5 вершинами

Лемма. Полный граф с пятью вершинами (К₅) нельзя уложить на плоскость.

Доказательство. Для него не выполняется .

22. Свойства из теоремы Эйлера

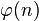
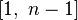
Функция Эйлера показывает, сколько натуральных чисел из отрезка имеют c только один общий делитель — единицу. Функция Эйлера определена на множественатуральных чисел, и значения её лежат в множестве натуральных чисел.

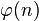
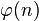
Как следует из определения, чтобы вычислить , нужно перебрать все числа от до и для каждого проверить, имеет ли оно общие делители с , а затем подсчитать, сколько чисел оказались взаимно простыми с . Эта процедура весьма трудоемка, поэтому для вычисления используют другие методы, которые основываются на специфических свойствах функции Эйлера.

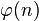
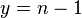
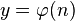
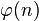
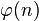
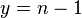
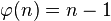
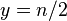
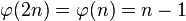
В таблице справа представлены первые 99 значений функции Эйлера. Анализируя эти данные, можно заметить, что значение не превосходит , и в точности ему равно, если — простое. Таким образом, если в координатах провести прямую , то значения будут лежать либо на этой прямой, либо ниже её. Также, глядя на график, приведенный в начале статьи, и на значения в таблице, можно предположить, что существует прямая, проходящая через ноль, которая ограничивает значения снизу. Однако, оказывается, такой прямой не существует. То есть, какую бы пологую прямую мы ни провели, всегда найдется натуральное число такое что лежит ниже этой прямой. Ещё одной интересной особенностью графика, является наличие некоторых прямых, вдоль которых концентрируются значения функции Эйлера. Так, например, помимо прямой , на которой лежат значения , где — простое, выделяется прямая, примерно соответствующая , на которую попадают значения , где — простое.

Более подробно поведение функции Эйлера рассматривается в разделе #Асимптотические соотношения.

23. Алгоритм укладки графа на плоскости

Для плоской укладки графа и попутной проверки, планарен ли он, удобно пользоваться гамма-алгоритмом.

На вход подаются графы, обладающие следующими свойствами:

граф имеет хотя бы один цикл;

граф не имеет мостиков, т. е. ребер, после удаления которых граф распадается на две компонеты связности.

Если нарушено свойство (1), то граф нужно укладывать отдельно по компонентам связности.

Если нарушено свойство (2), то граф — дерево и нарисовать его плоскую укладку тривиально.

Случай нарушения свойства (3) рассмотрим более подробно. Если в графе есть мостики, то их нужно разрезать, провести отдельно плоскую укладку каждой компоненты связности, а затем соединить их мостиками. Здесь может возникнуть трудность: в процессе укладки концевые вершины мостика могут спрятаться внутри плоского графа. Нарисуем одну компоненту связности и будем присоединять к ней другие последовательно. Каждую новую компоненту связности будем рисовать в той грани, в которой лежит концевая вершина соответствующего мостика. Так как граф связности мостиками компонент связности является деревом, мы сумеем получить плоскую укладку.

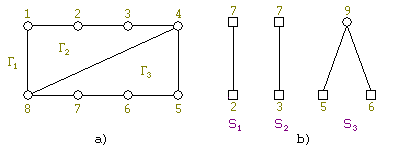
Сначала изложим алгоритм на конкретном примере. Пусть дан граф G (см. рис. 3).

Инициализация алгоритма производится так: выбираем любой простой цикл; в нашем примере <1, 2, 3, 4, 5, 6, 7, 8>и получаем две грани: Γ₁ — внешнюю и Γ₂ — внутреннюю (см. рис. 4).

Обозначим выбранный цикл как G ′. На каждом шаге будем строить множество сегментов. Каждый сегмент S относительно уже построенного графа G ′ представляет собой одно из двух:

ребро, оба конца которого принадлежат G ′, но само оно не принадлежит G ′;

Те вершины, которые одновременно принадлежат G ′ и какому-то сегменту, назовем контактными. Для нашего примера сегменты и вершины изображены на рис. 5. Контактные вершины обведены в квадрат.

Если бы в каком-нибудь сегменте не было ни одной контактной вершины, то граф до разрезания был бы несвязный; если бы была только одна, то граф имел бы мостик. Эти возможности заранее исключены, так что каждый сегмент имеет не менее двух контактных вершин. Поэтому в каждом сегменте имеется цепь между любой парой таких вершин.

Общий шаг алгоритма следующий: обозреваются все сегменты S_i и определяются числа |Γ( S_i )|. Если хоть одно из них равно 0, то граф не планарен, конец. Иначе, выбираем сегмент, для которого число |Γ( S )| минимально, или один из множества, если таких сегментов несколько. В этом сегменте найдем цепь между двумя контактными вершинами и уложим ее в любую из граней множества Γ( S ), совместив контактные вершины сегмента с соответствующими вершинами грани. При этом данная грань разобьется на две. Уже уложенная часть графа G ′ по количеству ребер и вершин увеличится, а сегмент, из которого вынута цепь, исчезнет или развалится на меньшие с новыми контактными вершинами, ведущими к вершинам G ′.

В результате повторения общего шага либо будет получена плоская укладка, когда множество сегментов станет пустым, либо будет получено, что граф G не является планарным.

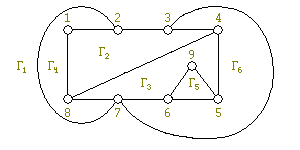
Вернемся к нашему примеру. Пока для любого i : S_i ⊂<Γ₁, Γ₂>, |Γ( S_i )| = 2. Поэтому возьмем первый по номеру сегмент S_i и в нем первую попавшеюся цепь <4, 8>; вставим эту цепь в грань Γ₂. Получим увеличенную часть G ′ и уменьшенную систему сегментов (см. рис. 6 a, b).

Определим какие грани вмещают новые сегменты. Теперь сегменты S ₁ и S ₂ вмещаются только в одну грань Γ₁, в то время, как сегмент S ₃ вмещается в две грани Γ₁ и Γ₃. Поэтому берем S ₁. Возьмем в нем цепь между контактными вершинами, например, <2, 7>, и уложим ее в Γ₁. Получим увеличенную часть G ′ и уменьшенную систему сегментов (см. рис. 7 a, b).

Продолжая таким образом, в итоге получим плоскую укладку G (см. рис. 8).

Еще раз опишем гамма-алгоритм компактно и займемся его обоснованием.

Гамма-алгоритм

(Инициализация). Выберем любой простой цикл C исходного графа G ; изобразим его на плоскости в виде грани, которую примем за уже уложенную часть G ′; сформируем сегменты S_i ; если множество сегментов пусто, то перейти к п. 3.

(Общий шаг). Пока множество сегментов непусто:

Выбираем один из сегментов с минимальным числом, вмещающих его граней.

Выбираем одну из подходящих граней для выбранного сегмента.

В данном сегменте выбираем цепь между двумя контактными вершинами и укладываем ее в выбранной грани. Учтем изменения в структуре сегментов и перейдем к п. a).

Эйлеров путь (эйлерова цепь) в графе — это путь (цепь), проходящий по всем дугам (рёбрам) графа и притом только по одному разу. (ср. Гамильтонов путь)

Эйлеров цикл — это цикл графа, проходящий через каждое ребро (дугу) графа ровно по одному разу.

Эйлеров граф — граф, содержащий эйлеров цикл.

Полуэйлеров граф — граф, содержащий эйлеров путь (цепь).

Источник