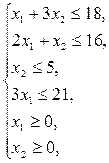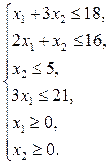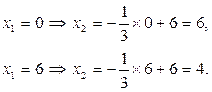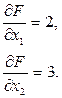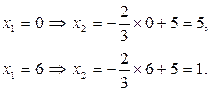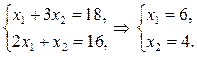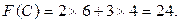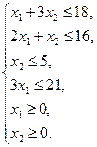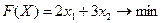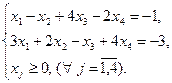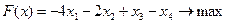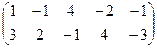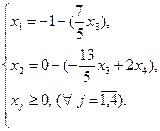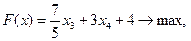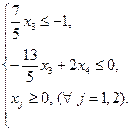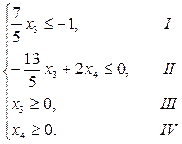что такое градиент целевой функции
Что такое градиент целевой функции
Графический метод характеризуется простотой и наглядностью, однако он недостаточно точен и применим только для задач с не более чем тремя переменными. Последнее обусловлено тем, что человек, живущий в трехмерном пространстве, практически не способен представить себе визуально пространство более высокого порядка.
Рассмотрим следующий простой пример решения задачи линейного программирования (ЗЛП) графическим методом.
Математическая модель: 2Х1+3Х2≤60;
3Х1+2Х2≤60;
4Х1+20Х2≤200;
Х1≥0; Х2≥0;
F=40Х1+30Х2→Мах.
Перейдем от неравенств к равенствам: 2Х1+3Х2=60;
3Х1+2Х2=60;
4Х1+20Х2=200.
Это уравнения прямых линий, которые могут быть легко построены по двум точкам:
для первого ограничения Х1=0; Х2=20;
Х2=0; Х1=30.
для второго ограничения Х1=0; Х2=30;
Х2=0; Х1=20.
для третьего ограничения Х1=0; Х2=10;
Х2=0; Х1=50.
Градиент целевой функции это вектор, характеризующий направление и скорость изменения функции (в данном случае целевой функции). Он определяется ее частными производными по каждой переменной:
Линия уровня целевой функции перпендикулярна градиенту.
Графическое решение данной задачи приведено на рисунке 6.1.
Рис. 6.1. Графическое решение задачи
Область допустимых решений (ОДР) в данном случае образуется четырехугольником ОВСД. Ни одна точка внутри его или на его границе не противоречит ни одному из ограничений. Оптимальное решение находится в одной из вершин четырехугольника. Для нахождения оптимального решения перемещаем линию уровня целевой функции в направлении градиента до крайней точки ОДР. Такой точкой является точка С с координатами: Х1=16; Х2=8. Значение целевой функции F=40×16+30×8=880. Очевидно, что это решение не отличается высокой точностью, что характерно для графического метода.
Из рисунка видно, что ресурсы второго и третьего видов использованы полностью, а ресурс первого вида оказался в избытке. Для количественной оценки этого избытка определим сначала расход данного ресурса: 2×16+3×8=56. Запас равен 60, тогда остаток составит 6056=4.
6.1.2. Симплексный метод решения
задач линейного программирования
В отличие от графического метода, симплексный метод абсолютно точен. Кроме того, он дает возможность для точной количественной оценки излишков имеющихся ресурсов, а применение двойственного симплекс-метода дает еще и большие возможности для технико-экономического анализа полученного решения с целью выработки обоснованных рекомендаций по улучшению условий функционирования системы.
Дополнительные переменные Х3, Х4 и Х5 равны разности между левой и правой частями ограничений и характеризуют недовыполнение данного ограничения (в данном случае излишний запас).
Задача решается в стандартных симплексных таблицах. Исходная таблица (см. табл. 6.1) заполняется коэффициентами модели.
| Базис | Х1 | Х2 | Х3 | Х4 | Х5 | а io | a io / a ip |
|---|---|---|---|---|---|---|---|
| Х3 | 2 | 3 | 1 | 0 | 0 | 60 | 20 |
| Х4 | 3 | 2 | 0 | 1 | 0 | 60 | 30 |
| Х5 | 4 | 20 | 0 | 0 | 1 | 200 | 10 |
| F | 4 | 3 | 0 | 0 | 0 | 0 |
Базисными переменными являются переменные, входящие только в одно уравнение, с коэффициентом +1. Базисным переменным соответствует единичный вектор-столбец. Базисные переменные равны свободным членам. Свободные переменные (переменные, не вошедшие в базис) равны нулю. Таким образом, Х1=0; Х2=0; Х3= 60; Х4= 60; Х5=200; F=0.
Данное решение является опорным, так как в столбце свободных членов нет отрицательных элементов.
В качестве разрешающего столбца выбирается любой столбец с отрицательной оценкой в строке целевой функции F. Выберем в данном случае в качестве разрешающего второй столбец. Для всех его элементов вычисляем симплексные отношения a io /a ip (отношение элемента столбца свободных членов к соответствующему элементу разрешающего столбца) и записываем их в последний столбец таблицы. Разрешающий элемент определяется минимальным симплексным отношением (в таблице он выделен жирным шрифтом). На месте разрешающего элемента ставится 1, а остальные элементы данного столбца равны нулю.
Остальные столбцы, соответствующие базисным переменным остаются без изменения. Столбец, соответствующий выводимой из базиса переменной, пересчитывается по общему правилу, описанному ниже. В данном случае Х2 вводится в базис вместо Х5 и столбец Х5 пересчитывается. Элементы разрешающей строки делятся на разрешающий элемент. Все остальные элементы таблицы пересчитываются по правилу прямоугольника. Пересчитываемый элемент образует с разрешающим элементом и соответствующими элементами разрешающей строки и столбца прямоугольник, изображенный на рисунке 6.2.
Рис. 6.2. Прямоугольник пересчета элементов симплексной таблицы
Пересчет производится по следующей формуле:
| (6.1) |
т.е. пересчитываемый элемент умножается на решающий элемент, минус элемент соответствующего разрешающего столбца, умноженный на соответствующий элемент разрешающей строки, и эта разность делится на разрешающий элемент. Или иначе: произведение элементов главной диагонали минус произведение элементов побочной диагонали, деленное на разрешающий элемент.
Например, пересчет элемента первого столбца первой строки:
| Базис | Х1 | Х2 | Х3 | Х4 | Х5 | а io | a io / a ip |
|---|---|---|---|---|---|---|---|
| Х3 | 1,4 | 0 | 1 | 0 | 0,15 | 30 | 21,4 |
| Х4 | 2,6 | 0 | 0 | 1 | 0,10 | 40 | 15,4 |
| Х2 | 0,2 | 1 | 0 | 0 | 0,05 | 10 | 50 |
| F | 3,4 | 0 | 0 | 0 | 0,150 | 300 |
Решение задачи на любой итерации читается следующим образом: базисные переменные равны свободным членам (предпоследний столбец в таблице) а свободные переменные (те, которые не входят в базис) равны нулю. В данном случае Х3 = 30; Х4 = 40; Х2 = 10; Х1 = Х5 = 0.
Или в краткой форме записи: Х1 = (0; 10; 30; 40; 0), F = 300.
Здесь значения переменных приводятся в порядке возрастания их индексов.
Технико-экономический анализ полученного решения
Выпускается десять единиц продукции второго вида (Х2 = 10). При этом ресурс второго вида останется в количестве тридцати единиц (Х3 = 30), ресурс первого вида останется в количестве сорока единиц (Х4 = 40), а ресурс третьего вида оказывается израсходованным полностью (Х5 = 0).
Проверка полученного решения: 2·0+3·10+30=60;
3·0+2·10+40=60;
4·0+20·10+0=200;
F=40·0+30·10=300.
Данное решение не является оптимальным, так как в строке целевой функции еще есть отрицательный элемент а 1F = 3,4.
Вторая и все последующие итерации выполняются аналогично.
| Базис | Х1 | Х2 | Х3 | Х4 | Х5 | а io | a io / a ip |
|---|---|---|---|---|---|---|---|
| Х3 | 0 | 0 | 1 | 0,54 | 0,1 | 8,5 | |
| Х1 | 1 | 0 | 0 | 0,38 | 0,04 | 15,4 | |
| Х2 | 0 | 1 | 0 | 0,74 | 0,17 | 6,9 | |
| F | 0 | 0 | 0 | 1,3 | 0,28 | 823 |
Х2=(15,4; 6,9; 8,5; 0; 0) → F=823.
Это решение оптимально, так как в строке целевой функции нет отрицательных оценок.
Технико-экономический анализ полученного решения
При имеющихся ресурсах следует выпустить 15,4 единицы (Х1=15,4) продукции первого вида и 6,9 единицы продукции второго вида (Х2=6,9). При этом ресурсы первого вида остаются в количестве 8,5 единицы (Х3=8,5), а ресурсы второго и третьего вида израсходованы полностью (Х4=Х5=0). Прибыль составит 823 у.е.
Проверка: 2·15,4+3·6,9+8,5=60;
3·15,4+2·6,9+0=60;
4·15,4+20·6,9+0=200;
F=40·15,4+30·6,9=823.
Сравнение полученных результатов с результатами графического метода подтверждает, что графический метод при всей своей наглядности не отличается достаточной точностью.
© ФГОУ ВПО Красноярский государственный аграрный университет
Графический (геометрический) метод решения задач ЛП



Пример 5.1.Решить следующую задачу линейного программирования геометрическим методом:
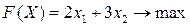
Решение:
Задача линейного программирования задана в стандартной форме и имеет два проектных параметра, следовательно, возможно ее решение геометрическим методом.
1 этап: построение прямых, ограничивающих область допустимых решений (ОДР).
Рассмотрим систему ограничений задачи линейного программирования (для удобства пронумеруем неравенства):
Рассмотрим первое ограничение, заменим знак неравенства знаком равенства и выразим переменную х2 через х1:
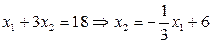
Для построения прямой по данному уравнению зададим две произвольные точки, к примеру:
Аналогично определяем точки для остальных ограничений системы и строим по ним прямые, соответствующие каждому неравенству (рис. 5.1). Прямые пронумеруем согласно принятой ранее схеме.
2 этап: определение решения каждого из неравенств системы ограничений.
Определим полуплоскости – решения каждого из неравенств.
Рассмотрим первое неравенство системы ограничений задачи. Возьмем какую-либо точку (контрольную точку), не принадлежащую соответствующей данному неравенству прямой, например, точку (0; 0). Подставим ее в рассматриваемое неравенство:
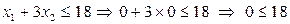
При подстановке координат контрольной точки неравенство остается справедливым. Следовательно, множество точек, принадлежащих данной прямой (т.к. неравенство не строгое), а также расположенных ниже ее, будут являться решениями рассматриваемого неравенства (пометим на графике (рис. 5.1) найденную полуплоскость двумя стрелками направленными вниз рядом с прямой I)[1].
Аналогично определяем решения других неравенств и соответственно помечаем их графике. В результате график примет следующий вид:
3 этап: определение ОДР задачи линейного программирования.
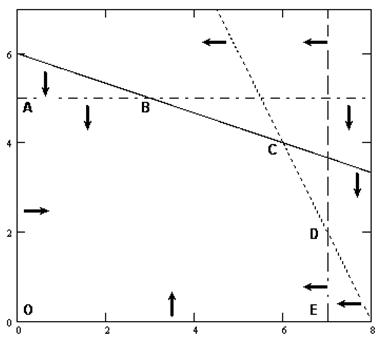
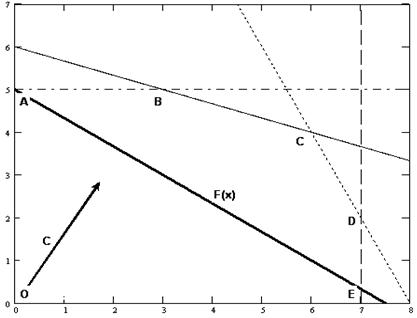
Найденные полуплоскости (решения каждого из неравенств системы ограничений) при пересечении образуют многоугольник ABCDEO, который и является ОДР рассматриваемой задачи.
Рис. 5.1. Область допустимых решений задачи
4 этап: построение вектора-градиента.
Вектор-градиент показывает направление максимизации целевой функции[2]. Определим его координаты: координаты начальной его точки (точки приложения) – (0; 0), координаты второй точки:
Построим данный вектор на графике (рис. 5.2).
5 этап: построение прямой целевой функции.
Рассмотрим целевую функцию данной задачи:
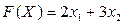
Зададим ей какое-либо значение, к примеру, 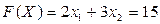
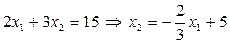
Для построения прямой по данному уравнению зададим две произвольные точки, к примеру:
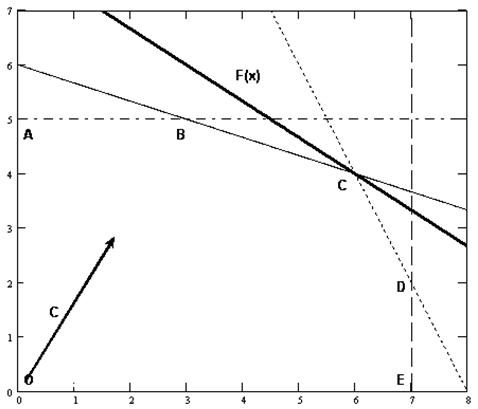
Построим прямую соответствующую целевой функции (рис. 5.2).

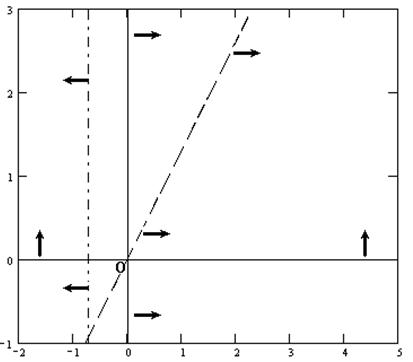
Рис. 5.2. Построение целевой функции F(X) и вектора-градиента С
6 этап: определение максимума целевой функции.
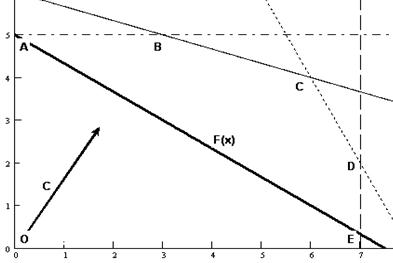
Перемещая прямую F(X) параллельно самой себе по направлению вектора-градиента, определяем крайнюю точку (точки) ОДР. Согласно графику (рис. 5.3), такой точкой является точка С – точка пересечения прямых I и II.

Рис. 5.3. Определение точки максимума целевой функции F(X)
Определим координаты точки С, с этой целью, решим следующую систему линейных уравнений:
Подставим найденные координаты в целевую функцию и найдем ее оптимальное (максимальное) значение:
Ответ: при заданных ограничениях максимальное значение целевой функции F(Х)=24, которое достигается в точке С, координаты которой х1=6, х2=4.
Пример 5.2. Решить задачу линейного программирования геометрическим методом:
Решение:
Этапы 1-3 аналогичны соответствующим этапам предыдущей задачи.
4 этап: построение вектора-градиента.
Построение вектора-градиента осуществляется аналогично, как и в предыдущей задаче. Построим данный вектор на графике (рис. 5.4). Отметим также на данном графике стрелкой направление, обратное вектору-градиенту, – направление минимизации целевой функции F(X).
5 этап: построение прямой целевой функции.
Построение прямой целевой функции F(X) осуществляется аналогично, как и в предыдущей задаче (результат построения приведен на рис. 5.4).
Рис. 5.4. Построение целевой функции F(x) и вектора-градиента С
6 этап: определение оптимума целевой функции.
Перемещая прямую F(x) параллельно самой себе в направлении, обратном вектору-градиенту, определяем крайнюю точку (точки) ОДР. Согласно графику (рис. 5.5), такой точкой является точка О с координатами (0; 0).
 |
Рис. 5.5. Определение точки минимума целевой функции
Подставляя координаты точки минимума в целевую функцию, определяем ее оптимальное (минимальное) значение, которое равно 0.
Ответ: при заданных ограничениях минимальное значение целевой функции F(Х)=0, которое достигается в точке О (0; 0).
Пример 5.3. Решить следующую задачу линейного программирования геометрическим методом:
Решение:
Рассматриваемая задача линейного программирования задана в канонической форме, выделим в качестве базисных переменные x1 и x2.
Составим расширенную матрицу и выделим с помощью метода Жордана-Гаусса базисные переменные x1 и x2.
Умножим (поэлементно) первую строку на –3 и сложим со второй:
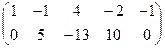
Умножим вторую строку на 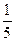
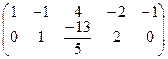
Сложим вторую с первой строкой:
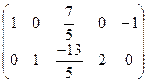
В результате система ограничений примет следующий вид:
Выразим базисные переменные через свободные:
Выразим целевую функцию также через свободные переменные, для этого подставим полученные значения базисных переменных в целевую функцию:
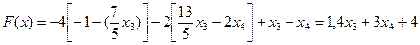
Запишем полученную задачу линейного программирования
Так как переменные x1 и x2 неотрицательные, то полученную систему ограничений можно записать в следующем виде:
Тогда исходную задачу можно записать в виде следующей эквивалентной ей стандартной задаче линейного программирования:
Данная задача имеет два проектных параметра, следовательно, возможно ее решение геометрическим методом.
1 этап: построение прямых, ограничивающих область допустимых решений (ОДР).
Рассмотрим систему ограничений задачи линейного программирования (для удобства пронумеруем неравенства):
Построим прямые, соответствующие каждому неравенству (рис. 5.6). Прямые пронумеруем согласно принятой ранее схеме.
2 этап: определение решения каждого из неравенств системы ограничений.
С помощью контрольных точек определим полуплоскости – решения каждого из неравенств, и пометим их на графике (рис. 5.6) с помощью стрелок.
3 этап: определение ОДР задачи линейного программирования.
Найденные полуплоскости (решения каждого из неравенств системы ограничений) не имеют общего пересечения (так решения неравенства I противоречат в целом остальным неравенствам системы ограничений), следовательно, система ограничений не совместна и задача линейного программирования в силу этого не имеет решения.
Рис. 5.6. Фрагмент MathCAD-документа:
построение области допустимых решений задачи
Ответ: рассматриваемая задача линейного программирования не имеет решения в силу несовместности системы ограничений.
Что такое градиент целевой функции
Графический метод характеризуется простотой и наглядностью, однако он недостаточно точен и применим только для задач с не более чем тремя переменными. Последнее обусловлено тем, что человек, живущий в трехмерном пространстве, практически не способен представить себе визуально пространство более высокого порядка.
Рассмотрим следующий простой пример решения задачи линейного программирования (ЗЛП) графическим методом.
Математическая модель: 2Х1+3Х2≤60;
3Х1+2Х2≤60;
4Х1+20Х2≤200;
Х1≥0; Х2≥0;
F=40Х1+30Х2→Мах.
Перейдем от неравенств к равенствам: 2Х1+3Х2=60;
3Х1+2Х2=60;
4Х1+20Х2=200.
Это уравнения прямых линий, которые могут быть легко построены по двум точкам:
для первого ограничения Х1=0; Х2=20;
Х2=0; Х1=30.
для второго ограничения Х1=0; Х2=30;
Х2=0; Х1=20.
для третьего ограничения Х1=0; Х2=10;
Х2=0; Х1=50.
Градиент целевой функции это вектор, характеризующий направление и скорость изменения функции (в данном случае целевой функции). Он определяется ее частными производными по каждой переменной:
Линия уровня целевой функции перпендикулярна градиенту.
Графическое решение данной задачи приведено на рисунке 6.1.
Рис. 6.1. Графическое решение задачи
Область допустимых решений (ОДР) в данном случае образуется четырехугольником ОВСД. Ни одна точка внутри его или на его границе не противоречит ни одному из ограничений. Оптимальное решение находится в одной из вершин четырехугольника. Для нахождения оптимального решения перемещаем линию уровня целевой функции в направлении градиента до крайней точки ОДР. Такой точкой является точка С с координатами: Х1=16; Х2=8. Значение целевой функции F=40×16+30×8=880. Очевидно, что это решение не отличается высокой точностью, что характерно для графического метода.
Из рисунка видно, что ресурсы второго и третьего видов использованы полностью, а ресурс первого вида оказался в избытке. Для количественной оценки этого избытка определим сначала расход данного ресурса: 2×16+3×8=56. Запас равен 60, тогда остаток составит 6056=4.
6.1.2. Симплексный метод решения
задач линейного программирования
В отличие от графического метода, симплексный метод абсолютно точен. Кроме того, он дает возможность для точной количественной оценки излишков имеющихся ресурсов, а применение двойственного симплекс-метода дает еще и большие возможности для технико-экономического анализа полученного решения с целью выработки обоснованных рекомендаций по улучшению условий функционирования системы.
Дополнительные переменные Х3, Х4 и Х5 равны разности между левой и правой частями ограничений и характеризуют недовыполнение данного ограничения (в данном случае излишний запас).
Задача решается в стандартных симплексных таблицах. Исходная таблица (см. табл. 6.1) заполняется коэффициентами модели.
| Базис | Х1 | Х2 | Х3 | Х4 | Х5 | а io | a io / a ip |
|---|---|---|---|---|---|---|---|
| Х3 | 2 | 3 | 1 | 0 | 0 | 60 | 20 |
| Х4 | 3 | 2 | 0 | 1 | 0 | 60 | 30 |
| Х5 | 4 | 20 | 0 | 0 | 1 | 200 | 10 |
| F | 4 | 3 | 0 | 0 | 0 | 0 |
Базисными переменными являются переменные, входящие только в одно уравнение, с коэффициентом +1. Базисным переменным соответствует единичный вектор-столбец. Базисные переменные равны свободным членам. Свободные переменные (переменные, не вошедшие в базис) равны нулю. Таким образом, Х1=0; Х2=0; Х3= 60; Х4= 60; Х5=200; F=0.
Данное решение является опорным, так как в столбце свободных членов нет отрицательных элементов.
В качестве разрешающего столбца выбирается любой столбец с отрицательной оценкой в строке целевой функции F. Выберем в данном случае в качестве разрешающего второй столбец. Для всех его элементов вычисляем симплексные отношения a io /a ip (отношение элемента столбца свободных членов к соответствующему элементу разрешающего столбца) и записываем их в последний столбец таблицы. Разрешающий элемент определяется минимальным симплексным отношением (в таблице он выделен жирным шрифтом). На месте разрешающего элемента ставится 1, а остальные элементы данного столбца равны нулю.
Остальные столбцы, соответствующие базисным переменным остаются без изменения. Столбец, соответствующий выводимой из базиса переменной, пересчитывается по общему правилу, описанному ниже. В данном случае Х2 вводится в базис вместо Х5 и столбец Х5 пересчитывается. Элементы разрешающей строки делятся на разрешающий элемент. Все остальные элементы таблицы пересчитываются по правилу прямоугольника. Пересчитываемый элемент образует с разрешающим элементом и соответствующими элементами разрешающей строки и столбца прямоугольник, изображенный на рисунке 6.2.
Рис. 6.2. Прямоугольник пересчета элементов симплексной таблицы
Пересчет производится по следующей формуле:
| (6.1) |
т.е. пересчитываемый элемент умножается на решающий элемент, минус элемент соответствующего разрешающего столбца, умноженный на соответствующий элемент разрешающей строки, и эта разность делится на разрешающий элемент. Или иначе: произведение элементов главной диагонали минус произведение элементов побочной диагонали, деленное на разрешающий элемент.
Например, пересчет элемента первого столбца первой строки:
| Базис | Х1 | Х2 | Х3 | Х4 | Х5 | а io | a io / a ip |
|---|---|---|---|---|---|---|---|
| Х3 | 1,4 | 0 | 1 | 0 | 0,15 | 30 | 21,4 |
| Х4 | 2,6 | 0 | 0 | 1 | 0,10 | 40 | 15,4 |
| Х2 | 0,2 | 1 | 0 | 0 | 0,05 | 10 | 50 |
| F | 3,4 | 0 | 0 | 0 | 0,150 | 300 |
Решение задачи на любой итерации читается следующим образом: базисные переменные равны свободным членам (предпоследний столбец в таблице) а свободные переменные (те, которые не входят в базис) равны нулю. В данном случае Х3 = 30; Х4 = 40; Х2 = 10; Х1 = Х5 = 0.
Или в краткой форме записи: Х1 = (0; 10; 30; 40; 0), F = 300.
Здесь значения переменных приводятся в порядке возрастания их индексов.
Технико-экономический анализ полученного решения
Выпускается десять единиц продукции второго вида (Х2 = 10). При этом ресурс второго вида останется в количестве тридцати единиц (Х3 = 30), ресурс первого вида останется в количестве сорока единиц (Х4 = 40), а ресурс третьего вида оказывается израсходованным полностью (Х5 = 0).
Проверка полученного решения: 2·0+3·10+30=60;
3·0+2·10+40=60;
4·0+20·10+0=200;
F=40·0+30·10=300.
Данное решение не является оптимальным, так как в строке целевой функции еще есть отрицательный элемент а 1F = 3,4.
Вторая и все последующие итерации выполняются аналогично.
| Базис | Х1 | Х2 | Х3 | Х4 | Х5 | а io | a io / a ip |
|---|---|---|---|---|---|---|---|
| Х3 | 0 | 0 | 1 | 0,54 | 0,1 | 8,5 | |
| Х1 | 1 | 0 | 0 | 0,38 | 0,04 | 15,4 | |
| Х2 | 0 | 1 | 0 | 0,74 | 0,17 | 6,9 | |
| F | 0 | 0 | 0 | 1,3 | 0,28 | 823 |
Х2=(15,4; 6,9; 8,5; 0; 0) → F=823.
Это решение оптимально, так как в строке целевой функции нет отрицательных оценок.
Технико-экономический анализ полученного решения
При имеющихся ресурсах следует выпустить 15,4 единицы (Х1=15,4) продукции первого вида и 6,9 единицы продукции второго вида (Х2=6,9). При этом ресурсы первого вида остаются в количестве 8,5 единицы (Х3=8,5), а ресурсы второго и третьего вида израсходованы полностью (Х4=Х5=0). Прибыль составит 823 у.е.
Проверка: 2·15,4+3·6,9+8,5=60;
3·15,4+2·6,9+0=60;
4·15,4+20·6,9+0=200;
F=40·15,4+30·6,9=823.
Сравнение полученных результатов с результатами графического метода подтверждает, что графический метод при всей своей наглядности не отличается достаточной точностью.
© ФГОУ ВПО Красноярский государственный аграрный университет