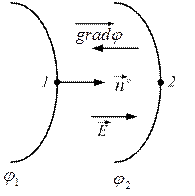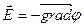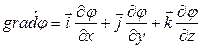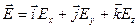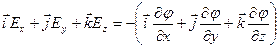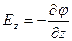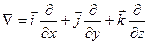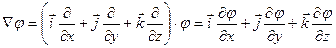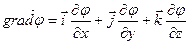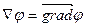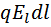что такое градиент потенциала

Градиент потенциала

Градиент потенциала – это скорость возрастания потенциала в направлении кротчайшем между двумя точками.

Между двумя точками имеется некоторая разность потенциалов. Если эту разность разделить на кратчайшее расстояние между взятыми точками, то полученное значение будет характеризовать скорость изменения потенциала в направлении кратчайшего расстояния между точками.

Градиент потенциала показывает направление наибольшего возрастания потенциала, численно равен модулю напряженности и отрицательно направлен по отношению к нему.

В определении градиента существенны два положения:

1) Направление, в котором берутся две близлежащие точки, должно быть таким, чтобы скорость изменения была максимальной.

2) Направление таково, что скалярная функция в этом направлении возрастает.

Для декартовой системы координат:

Скорость изменения потенциала в направлении оси Х, Y, Z:

; ;

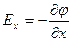
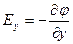
Два вектора равны только тогда, когда равны друг другу их проекции. Проекция вектора напряженности на ось Х равна проекции скорости изменения потенциала вдоль оси Х, взятой с обратным знаком. Аналогично для осей Y и Z.

; ; .

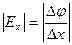
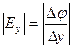
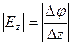
В цилиндрической системе координат выражение градиента потенциала будет иметь следующий вид:

.

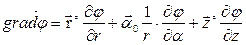
А в сферической системе координат:

.

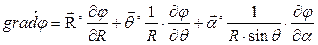
Дифференциальный оператор Гамильтона (оператор Набла)

Для сокращения записи операций над скалярными и векторными величинами употребляют дифференциальный оператор Гамильтона или оператор Набла:

Под дифференциальным оператором Гамильтона понимают сумму частных производных по 3-м координатным осям, умноженных на соответствующие единичные векторы (орты).

Применим оператор Гамильтона к потенциалу:

Правые части одинаковы, значит, будут одинаковы и левые части:

Оператор Гамильтона сочетает в себе как векторные, так и скалярные свойства и может быть применен к скалярным и векторным функциям.

Дата добавления: 2015-07-30 ; просмотров: 19061 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Потенциал

Электрическое поле характеризуется тем, что работа перемещения заряда в поле не зависит от пути перехода из начального положения и является функцией только начального и конечного положений. Работа перемещения заряда по замкнутому контуру в электростатическом поле равна нулю. Из этих фактов следует, что электростатическое поле носит потенциальный характер и характеризуется особой величиной –
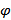
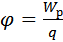
потенциалом . Величина

, (12)

Где W_р – потенциальная энергия заряда q, называется потенциалом поля в данной точке и используется наряду с напряженностью поля 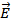для описания электрических полей.

Как следует из приведенной формулы, потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд.

В то время, как напряженности поля складываются при наложении полей векторно, потенциалы складываются алгебраически. По этой причине вычисление потенциалов проще, чем вычисление напряженностей поля.

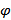
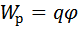
Из (12) вытекает, что заряд q, находящийся в точке поля с потенциалом , обладает потенциальной энергией

.

Следовательно, работа сил над зарядом q может быть выражено через разность потенциалов

.

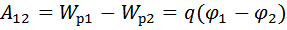
Таким образом, работа, совершаемая над зарядом силами поля, равна произведению величины заряда на разность потенциалов в начальной и конечной точках.

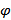
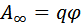
Если заряд q из точки с потенциалом удаляется на бес­конечность, где по условию потенциал равен нулю, то работа сил поля равна

.

Отсюда следует, что потенциал численно равен работе, которую совершают силы поля над единичным положительным зарядом при уда­лении его из денной точки на бесконечность.

Эквипотенциальные поверхности.

Для наглядного изображения поля можно вместо линий напряженнос­тей воспользоваться поверхностями равного потенциала или эквипо­тенциальными поверхностями.

Воображаемая поверхность, все точки которой имеют одинаковый потенциал, называется эквипотенциальной поверхностью.

Если потенциал задан как функция X, Y, Z, то уравнение эквипотенциальной поверхности имеет вид:

(x,y,z) = const.

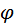
Эти поверхности проводятся в пространстве таким образом, чтобы численное значение потенциала на двух соседних поверхностях от­личалось повсюду на одинаковую величину ∆ 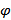(например на I В).

В качестве примера рассмотрим эквипотенциальные поверхности поля точечного заряда 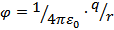. Отсюда следует, что при r = const т.е. поверхности равного потенциала будут концентрическими сферами, описанными вокруг источника поля на возрастающих расстояниях друг от друга, как это показано на рис.4.

Проведем на рис.4 линии напряженности поля. Эти линии выходят из точечного заряда и направ­лены вдоль радиусов, т.е. перпендикулярны к эквипотенциальным поверхностям.

Эта взаимная перпендикулярность линий поля и эквипотенциальных поверхностей остается справедливой и для сколь угодно сложных электро­статических полей.

Градиент потенциала. Связь между напряжен­ностью и потенциалом.

Работа сил поля над зарядом q на отрезке пути dl мо­жет быть представлена с одной стороны, как

В частности, в декартовой системе координат:

; ; ;

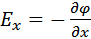
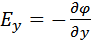
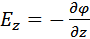
откуда .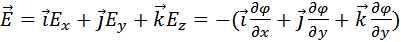

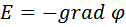
. (13)

Таким образом, напряженность электрического поля равна градиенту потенциала, взятому с обратным знаком.

Источник

Градиент потенциальных характеристик, как его рассчитать и пример

градиент потенциала является вектором, который представляет отношение изменения электрического потенциала по отношению к расстоянию в каждой оси декартовой системы координат. Таким образом, вектор градиента потенциала указывает направление, в котором скорость изменения электрического потенциала больше, в зависимости от расстояния.

В свою очередь, модуль градиента потенциала отражает скорость изменения электрического потенциала в определенном направлении. Если значение этого известно в каждой точке пространственной области, то электрическое поле может быть получено из градиента потенциала.

Электрическое поле определяется как вектор, с которым оно имеет определенное направление и величину. Определяя направление, в котором электрический потенциал уменьшается быстрее, удаляясь от контрольной точки, и деля это значение на пройденное расстояние, получается величина электрического поля..

черты

Градиент потенциала представляет собой вектор, ограниченный конкретными пространственными координатами, который измеряет отношение изменения между электрическим потенциалом и расстоянием, пройденным этим потенциалом.

Наиболее выдающиеся характеристики градиента электрического потенциала подробно описаны ниже:

2- Поскольку потенциальный градиент является вектором в пространстве, он имеет величины, адресованные по осям X (ширина), Y (высокая) и Z (глубина), если в качестве эталонной системы координат берется декартова система координат.

3- Этот вектор перпендикулярен эквипотенциальной поверхности в точке, в которой оценивается электрический потенциал.

4- Вектор градиента потенциала направлен в направлении максимального изменения функции электрического потенциала в любой точке..

5- Модуль градиента потенциала равен модулю, полученному из функции электрического потенциала по отношению к расстоянию, пройденному в направлении каждой из осей декартовой системы координат..

6- Потенциальный градиент имеет нулевое значение в стационарных точках (максимальная, минимальная и седловая точки).

7- В международной системе единиц (СИ) единицами измерения градиента потенциала являются вольт / метры.

8. Направление электрического поля такое же, в котором электрический потенциал уменьшает свою величину быстрее. В свою очередь, градиент потенциала указывает в направлении, в котором потенциал увеличивает свое значение по отношению к изменению положения. Тогда электрическое поле имеет то же значение градиента потенциала, но с противоположным знаком.

Как рассчитать?

Разность электрических потенциалов между двумя точками (точка 1 и точка 2) определяется следующим выражением:

V1: электрический потенциал в точке 1.

V2: электрический потенциал в точке 2.

E: величина электрического поля.

Ѳ: угол наклона вектора электрического поля, измеренного относительно системы координат.

Выражая указанную формулу дифференциальным способом, получаем следующее:

Далее, отношение между изменением электрического потенциала (dV) и изменением пройденного расстояния (ds) является модулем градиента потенциала для упомянутого компонента.

Из этого следует, что величина градиента электрического потенциала равна компоненте электрического поля в направлении исследования, но с противоположным знаком.

Однако, поскольку реальная среда является трехмерной, градиент потенциала в данной точке должен быть выражен как сумма трех пространственных компонентов на осях X, Y и Z декартовой системы..

Разбивая вектор электрического поля на три прямоугольных компонента, мы получаем следующее:

Если в плоскости имеется область, в которой электрический потенциал имеет одинаковое значение, частная производная этого параметра по каждой из декартовых координат будет равна нулю.

Таким образом, в точках, которые находятся на эквипотенциальных поверхностях, напряженность электрического поля будет иметь нулевую величину.

Наконец, вектор градиента потенциала может быть определен как точно такой же вектор электрического поля (по величине) с противоположным знаком. Таким образом, мы имеем следующее:

пример

Из приведенных выше расчетов необходимо:

Теперь, прежде чем определять электрическое поле как функцию градиента потенциала или наоборот, сначала необходимо определить направление, в котором разность электрических потенциалов растет..

После этого определяется коэффициент изменения электрического потенциала и изменения пройденного расстояния..

Таким образом, мы получаем величину соответствующего электрического поля, которая равна величине градиента потенциала в этой координате.

осуществление

Есть две параллельные пластины, как показано на следующем рисунке.

Шаг 1

Направление роста электрического поля на декартовой системе координат определяется.

Электрическое поле растет только в горизонтальном направлении, учитывая расположение параллельных пластин. Следовательно, можно сделать вывод, что компоненты градиента потенциала на оси Y и оси Z равны нулю..

Шаг 2

Данные, представляющие интерес различаются.

— Разница в расстоянии: дх = 10 сантиметров.

Чтобы обеспечить соответствие единиц измерения, используемых в соответствии с Международной системой единиц, величины, не выраженные в СИ, должны быть соответственно преобразованы. Таким образом, 10 сантиметров равны 0,1 метра, и, наконец, dx = 0,1 м.

Шаг 3

Величина вектора градиента потенциала рассчитывается соответствующим образом.

Источник

ПО­ЛЯ. ГРАДИЕНТ ПОТЕНЦИАЛА.

Для понимания свойств электрического поля большое значение имеет по­нятие разности потенциалов или электрического напряжения.К этому по­нятию мы придем, рассматривая работу сил электрического поля.

Допустим, что это не так, и что работа А ( L ) ₁₂ при перемещении заряда вдоль контура L (рис.12) не равна работе А ( L ’) ₁₂ для контура L’, причём оба контура соединяют одни и те же точки 1 и 2.

+1

Тогда перемещая заряд по замкнутому контуру, составленному из контуров L и L’, мы найдём, что электрические силы совершают работу

которая не равна нулю. Но это противоречит общему закону сохране­ния энергии. Если заряды, создающие электрическое поле, неподвижны, то при пере­мещении подвижного заряда в окружающих телах не происходит никаких процессов. После возвращения заряда в исходную точку 1 мы не имеем никаких изменений в рассматриваемой системе тел и поэтому не можем получить ни выигрыша работы, ни её потери. Это значит, что наше пред­положение неверно, и что в действительности

Т.о., в электростатическом поле работа перемещении заряда между дву­мя точками не зависит от формы пути, соединяющего эти точки.Иными словами: при перемещении заряда в электростатическом поле по замкну­тому контуру работа равна нулю.

« = ₁ + ₂ +….+ _n,

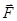
а работа А равнодействующей силы равна алгебраической сумме работ составляю­щих сил

Работа, совершаемая силой `F при перемещении заряда q₀ на отрезке d,

где

-угол между направлениями векторов `Е и dl.

В случае конечного перемещения заряда q₀ източки а в точкув работа сил поля

Этот интеграл называется циркуляцией напряженностивдоль замкнутого кон­тура L.

Поскольку работа при перемещении заряда по любому замкнутому контуру равна нулю, то

Т.е. циркуляция напряженности электростатического поля вдоль замкнутого контура равна нулю.Силовое поле, напряжённость Е которого удовлетворяет такому условию, называется потенциальным полем.Т.о. электростатическое поле является потен­циальным.

РАЗНОСТЬ ПОТЕНЦИАЛОВ.Если в электрическом поле перемещается заряд (+1), то работа зависит только от существующего электрического поля и поэтому мо­жет служить его характеристикой. Она называется разностью потенциаловточек 1 и 2 в данном электрическом поле или электрическим напряжениеммежду точками 1 и 2.

Разность потенциалов двух точек 1 и 2 в электростатическом поле изме­ряется работой, совершаемой силами поля при перемещении заряда (+1) из точки 1 в 2, т.е.

Если в электрическом поле перемещается не единичный заряд, а заряд произвольной величины q, то в каждой точке сила, действующая на заряд, увеличится в q раз. Поэтому работа А₁₂, совершаемая силами поля при перемещении q из 1 в 2,равна

Если заряд (+1) перемещается по замкнутому контуру, например, сначала из 1 в 2 по контуру L (рис.12), а затем от 2 к 1 вдоль L’, то

Источник

Градиента потенциала.

В электростатическом поле между двумя близко расположенными точками в общем случае имеется некоторая разность потенциалов. Если эту разность потенциалов разделить на кратчайшее расстояние между взятыми точками, то полученная величина будет характеризовать скорость изменения потенциала в направлении кратчайшего расстояния между точками. Эта скорость будет зависеть от направления, вдоль которого взяты точки.

В математике используют понятие градиента скалярной функции, под которым понимают скорость изменения скалярной функции, взятую в направлении ее наибольшего возрастания.

Возьмем две близко расположенные эквипотенциальные линии. Одна из них имеет потенциал φ₁, другая – φ₂, причем φ₁ > φ₂ (рис. 38.3). Тогда градиент изобразится вектором, перпендикулярным к эквипотенциальным линиям и направленным от φ₂ к φ₁ (в сторону увеличения потенциала).

Напряженность электрического поля направлена от более высокого потенциала (φ₁) к менее высокому (φ₂). Если через dn обозначить расстояние по нормали между эквипотенциальными поверхностями, а через вектор, совпадающий с направлением напряженности поля , т.е. ( – единичный вектор, направленный по направлению ), то можно записать выражение

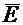
где – приращение потенциала при переходе от точки 1 к точке 2.

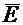
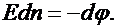
Так как векторы и совпадают по направлению, то . Таким образом Отсюда . Вектор напряженности поля . Поэтому

(38.5)

Из определения градиента следует, что

(38.6)

Сопоставляя (19.5) и (19.6), получаем

.

(38.7)

Физический смысл выражения (38.7) заключается в том, что напряженность поля в какой-либо его точке равна скорости изменения потенциала в этой точке, взятой с обратным знаком.

Нормаль в общем случае может не совпадать с направлением какой-либо координатной оси, и поэтому градиент потенциала в общем случае можно представить в виде суммы трех проекций по координатным осям. Например, в декартовой системе координат

(38.8)

Вектор напряженности поля Таким образом,

=

Два вектора равны только тогда, когда равны друг другу их соответствующие проекции. Следовательно

(38.9)

Для сокращения записи в математике используют дифференциальный оператор Гамильтона: используя который можно записать

Вопросы для самоконтроля

1. Какова основная отличительная особенность электромагнитного поля как вида материи?

2. Какими двумя сторонами характеризуется электромагнитное поле? Как эти стороны связаны между собой?

3. Охарактеризуйте понятие «электрическое поле».

4. Какими двумя основными величинами характеризуется электрическое поле?

5. Дайте определение потенциала электрического поля.

6. Какие поля называют потенциальными? Почему суммарная работа по переносу электрического заряда по замкнутому контуру в потенциальном поле равна нулю?

7. Что понимают под силовой линией электрического поля?

8. Какая поверхность в электрическом поле называется эквипотенциальной?

9. В чем смысл знака минус в формуле

10. Могут ли быть замкнутыми силовые линии в электростатическом поле?

Источник