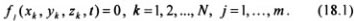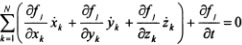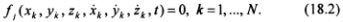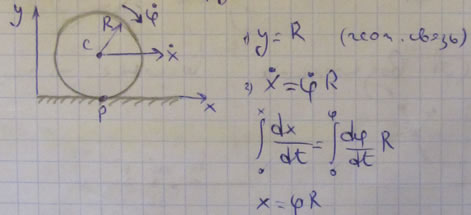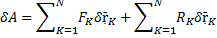что такое голономные связи
Что такое голономные связи
Связи и их классификация.
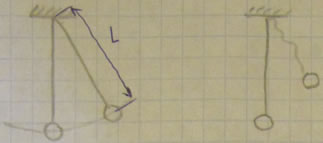
Связь называется удерживающей (двухсторонней), если она описывается уравнением (равенством). Голономную стационарную удерживающую связь, наложенную на материальную точку, можно представить в виде двух бесконечно близких одинаковых поверхностей, между которыми только и может находиться точка. Неудерживающая (односторонняя) связь описывается неравенством. Например, если математический маятник представляет собой тонкий стержень длиной l, вращающийся вокруг неподвижной оси и к свободному концу которого прикреплен груз (материальная точка), то связь для груза будет удерживающая. Если же груз прикреплен к свободному концу нерастяжимой нити длиной l. то связь будет неудерживающая, поскольку груз может находиться как на поверхности сферы радиусом l, так и внутри нее.
Механическая система, точки которой могут занимать любое положение в пространстве и иметь любые скорости, называется свободной. Например, свободной системой является космический аппарат, движущийся по орбите вокруг Земли. Его движение не ограничено другими телами и поэтому, прикладывая к аппарату соответствующие силы, можно изменять траекторию его центра масс и поворачивать аппарат вокруг центра масс. Если на координаты и скорости точек системы наложены ограничения, то система называется несвободной, а ограничения называются связями. Механические связи реализуются в виде различных устройств или тел (стержни, нити, шарниры и т. п.). Аналитически связь описывается уравнением вида: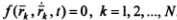 
.
Ограничивая движение механической системы, связи действуют на ее точки посредством сил, которые называются реакциями
связей. При изучении равновесия и движения механических систем методами аналитической механики применяется принцип
освобождения (аксиома о связях). Этот принцип состоит в том, что любую систему можно рассматривать как свободную, приложив к ее точкам реакции, соответствующие отброшенным связям.
Связи называются галономными, если они описываются уравнениями вида: 
Такие связи накладывают ограничения на координаты точек, а значит, на положение системы в пространстве. Это так называемые геометрические связи. Вместе с тем голономные связи накладывают ограничения и на скорости точек системы. Соответствующие условия получаются в результате дифференцирования уравнений (18.1) по времени:
Голономные связи могут описываться и дифференциальными уравнениями, однако последние обязательно должны быть интегрируемыми.
Неголономными называются связи, которые описываются уравнениями вида:
Уравнения (18.2), в отличие от уравнений голономных связей, не могут быть проинтегрированы независимо от дифференциальных уравнений движения системы. Неголономные связи накладывают ограничения (18.2) на скорости точек, поэтому их называют кинематическими.
Связи подразделяются на стационарные и нестационарные в зависимости от того, входит в явном виде время в уравнение связи или нет. Связь, уравнение которой имеет вид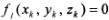 
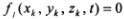
, является голономной и стационарной. Для голономной нестационарной связи уравнение будет таким: 
.
Например, жесткий стержень длиной l, прикрепленный к неподвижной опоре, является стационарной связью для материальной точки, находящейся на его свободном конце. Уравнение связи в декартовой системе координат, начало которой совпадает с точкой закрепления стержня, имеет вид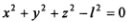 
.
(При вращении стержня вокруг опоры точка находится на сфере радиусом l.) Если длина стержня изменяется по заданному закону, то связь является нестационарной и ее уравнение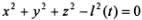 
.
Связь называется удерживающей (двухсторонней), если она описывается уравнением (равенством). Голономную стационарную удерживающую связь, наложенную на материальную точку, можно представить в виде двух бесконечно близких одинаковых поверхностей, между которыми только и может находиться точка. Неудерживающая (односторонняя) связь описывается неравенством. Например, если математический маятник представляет собой тонкий стержень длиной l, вращающийся вокруг неподвижной оси и к свободному концу которого прикреплен груз (материальная точка), то связь для груза будет удерживающая. Если же груз прикреплен к свободному концу нерастяжимой нити длиной l. то связь будет неудерживающая, поскольку груз может находиться как на поверхности сферы радиусом l, так и внутри нее.
Из лекций:
Классификация связей:
1) Геометрические связи.
2) Кинематические связи.
a) интегрируемые; (геометрические, интегрируемые кинематические = голономные)
б) неинтегрируемые; (геометрические, неинтегрируемые кинематические = неголономные)
3) Стационарная связь (склерономная).
Если t входит в уравнение явным образом, то связь нестационарная (реономная).
4) Освобождающие и неосвобождающие связи.
(неосвобождающая связь) ; (освобождающая связь)
x 2 +y 2 +z 2 =l 2 ; x 2 +y 2 +z 2 2
5) Идеальные и реальные связи.
Если у какой-то связи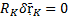 
(RK тоже вектор), то связь называется идеальной.
Если вся сумма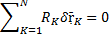 
, то механическая система с идеальными связями.
Реальные связи: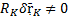 
.
Примеры идеальных связей: внутренние связи в абсолютно твердых телах; абсолютно гладкие поверхности; шарниры без трения; нерастяжимые нити; закрепленные точки; качение без скольжения.
Примеры реальных связей: шероховатая поверхность; шарниры с трением; упругие растяжимые нити; пружины; качение с проскальзыванием.
Замечание: всякую реальную связь можно сделать идеальной.
ГОЛОНОМНЫЕ СИСТЕМЫ
Полезное
Смотреть что такое «ГОЛОНОМНЫЕ СИСТЕМЫ» в других словарях:
Голономные системы — механические системы, в которых все связи (см. Связи механические) являются геометрическими (голономными), то есть налагающими ограничения только на положения (или перемещения за время движения) точек и тел системы, но не на величины их… … Большая советская энциклопедия
Неголономные системы — механические системы, на которые, кроме геометрических, налагаются ещё кинематические связи, не сводящиеся к геометрическим и называемые неголономными (см. Голономные системы). Примером Н. с. является шар, катящийся без проскальзывания по … Большая советская энциклопедия
НЕГОЛОНОМНЫЕ СИСТЕМЫ — механич. системы, на к рые, кроме геометрических, налагаются ещё кинематич. связи, не сводящиеся к геометрическим и наз. неголономными (см. ГОЛОНОМНЫЕ СИСТЕМЫ). Пример Н. с. шар, катящийся без проскальзывания по шероховатой плоскости. При этом… … Физическая энциклопедия
СВЯЗИ МЕХАНИЧЕСКИЕ — ограничения, налагаемые на положение или движения механич. системы. Обычно С. м. осуществляются с помощью к. н. тел. Примеры таких С. м. поверхность, по к рой скользит или катится тело; нить, на к рой подвешен груз; шарниры, соединяющие звенья… … Физическая энциклопедия
Лагранжа уравнения — 1) в гидромеханике уравнения движения жид кой среды, записанные в переменных Лагранжа, которыми являются координаты частиц среды. Из Л. у. определяется закон движения частиц среды в виде зависимостей координат от времени, а по ним… … Большая советская энциклопедия
Связи механические — ограничения, налагаемые на положение или движение механической системы. Обычно С. м. осуществляются с помощью каких нибудь тел. Примеры таких С. м.: поверхность, по которой скользит или катится тело; нить, на которой подвешен груз;… … Большая советская энциклопедия
Степеней свободы число — в механике, число независимых между собой возможных перемещений (См. Возможные перемещения) механической системы. С. с. ч. зависит от числа материальных частиц, образующих систему, и числа и характера наложенных на систему связей… … Большая советская энциклопедия
Голономная связь — Голономная связь механическая связь, налагающая ограничения только на положения (или перемещения) точек и тел системы. Математически выражается в виде равенства[1]: где qj обобщённые координаты, описывающие механическую систему, i=1…k … Википедия
Что такое голономные связи
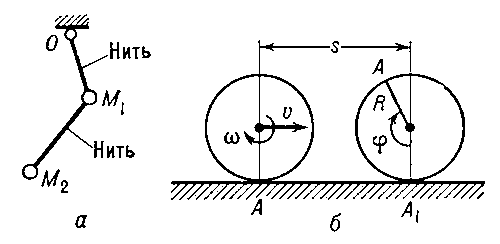
Кинематические связи не всегда имеют вид соотношений между координатами частиц. Случается, что имеют место условия более общей природы, которые можно записать лишь в дифференциальной форме. Характерным примером является шар, катящийся по столу. Шар, свободно перемещающийся в пространстве, имеет шесть степеней свободы. Если же он движется по плоскости, то высота центра тяжести остается постоянной, что уменьшает число степеней свободы до пяти. Мы можем описать положение шара двумя прямоугольными координатами х и у точки контакта шара с плоскостью и тремя углами а, 
которые фиксируют положение шара относительно системы неподвижных осей. Если шар может двигаться с проскальзыванием, то он действительно имеет все пять степенен свободы. Однако если он вынужден катиться без скольжения, то мгновенная скорость
в точке касания должна равняться нулю и мгновенная ось вращения должна проходить через точку касания. Если мгновенная ось вращения все время находится в плоскости стола, то мы имеем «чистое качение», в противном случае — «качение» с «верчением». В случае чистого качения число степеней свободы уменьшается до двух. Если путь точки контакта определен заданием х и у как функций времени 
то положение шара этим самым однозначно определено в любой момент времени. Может показаться, что углы 
могут быть заданы как функции х и у. Это, однако, невозможно. Дифференциалы 
выражаются через дифференциалы 
, но эти соотношения неинтегрируемы. Их нельзя заменить эквивалентными конечными соотношениями между координатами. Действительно, представим себе, что качение шара начинается с какого-то определенного положения и заканчивается при некотором фиксированном значении х и у. Если шар двигался двумя различными путями, то и конечные положения его окажутся повернутыми относительно друг друга; а если бы 
уможно было задать в виде функций х и у, то конечные положения шара в обоих случаях совпадали бы.
Подобные кинематические связи, которые могут быть заданы только в виде соотношений между дифференциалами координат, были названы Герцем «неголономными», в отличие от обычных «голономных» связей. Кинематическая связь вида
является голономной, хотя из (1.6.1) и следует при помощи дифференцирования, что
Если же мы начнем с дифференциального соотношения вида
заданные функции величин 
то его можно перевести в соотношение (1.6.1) лишь при выполнении определенных условий интегрируемости. Единственным исключением является случай 
потому что дифференциальные соотношения между двумя переменными всегда интегрируемы.
При помощи одних дифференцирований и исключений переменных всегда можно определить, является ли данная совокупность дифференциальных условий голономной или нет. Покажем, как это делается, на простейшем примере одного соотношения между тремя переменными; обобщение на случай большего количества уравнений и переменных следует автоматически. Сначала запишем заданное условие в виде:
Если эта связь допускает конечное соотношение между 
то должно иметь место равенство
или, точнее, поскольку 
могут зависеть неявно от 
Величины 
известны из (1.6.4); поэтому
Это равенство должно выполняться при любых и 
т. е. оно должно быть тождеством. Если это имеет место, то выражение (1.6.4) интегрируемо, в противном случае — нет. Может случиться, однако, что 
не выпадает из результирующего уравнения (1.6.7), а выражается через 
Тогда следует проверить, будут ли частные производные от 
по 
равны 
как это должно быть согласно (1.6.4). Если будут, то мы тем самым доказали, что данная связь голономна, и заменили ее дифференциальное выражение конечным. В случае более чем двух независимых переменных все условия интегрируемости
должны быть исследованы подобным же образом. Если задана целая система независимых дифференциальных соотношений, то следует сначала их разрешить относительно некоторых зависимых дифференциалов, а затем аналогично предыдущему проверить условия интегрируемости.
Задача. Исследовать интегрируемость следующего дифференциального соотношения
(Это условие голономно и может быть заменено конечным соотношением
Голономные кинематические связи можно использовать двумя путями. Во-первых, при наличии 
уравнений с 
переменными можно исключить часть переменных и свести задачу к 
независимым переменным. Во-вторых, можно оперировать с полным числом переменных, сохраняя заданные соотношения в качестве дополнительных условий.
Неголономные связи допускают лишь второй способ решения. Уменьшение числа переменных здесь невозможно и приходится оперировать с большим количеством переменных, чем того требует число степеней свободы системы. Пространство конфигураций в этом случае является частью пространства большего числа измерений, но не образует в нем определенного подпространства, потому что кинематические условия в каждой точке порождают пучок направлений, но эти пучки не имеют огибающей поверхности.
С точки зрения вариационных принципов механики голономные и неголономные связи различаются очень сильно. Хотя уравнения механики и могут быть написаны в случае неголономных связей, но эти уравнения нельзя получить из общего принципа, приравнивая нулю вариацию от определенной величины (гл. II, п. 13).
Резюме. Кинематические условия не всегда имеют вид конечных соотношений между координатами, иначе говоря, не всегда являются «голономными». Может случиться, что связи представимы лишь в виде соотношений между дифференциалами от координат. Такие связи называют «неголономными». Подобные связи возникают, например, при качении твердого тела без скольжения по некоторой поверхности.
Голономные системы
Полезное
Смотреть что такое «Голономные системы» в других словарях:
ГОЛОНОМНЫЕ СИСТЕМЫ — механич. системы, в к рых все связи (см. СВЯЗИ МЕХАНИЧЕСКИЕ) явл. геометрическими (голономными), т. е. налагающими ограничения только на положения (или на перемещения за время движения) точек и тел системы, но не на величины их скоростей. Напр.,… … Физическая энциклопедия
Неголономные системы — механические системы, на которые, кроме геометрических, налагаются ещё кинематические связи, не сводящиеся к геометрическим и называемые неголономными (см. Голономные системы). Примером Н. с. является шар, катящийся без проскальзывания по … Большая советская энциклопедия
НЕГОЛОНОМНЫЕ СИСТЕМЫ — механич. системы, на к рые, кроме геометрических, налагаются ещё кинематич. связи, не сводящиеся к геометрическим и наз. неголономными (см. ГОЛОНОМНЫЕ СИСТЕМЫ). Пример Н. с. шар, катящийся без проскальзывания по шероховатой плоскости. При этом… … Физическая энциклопедия
СВЯЗИ МЕХАНИЧЕСКИЕ — ограничения, налагаемые на положение или движения механич. системы. Обычно С. м. осуществляются с помощью к. н. тел. Примеры таких С. м. поверхность, по к рой скользит или катится тело; нить, на к рой подвешен груз; шарниры, соединяющие звенья… … Физическая энциклопедия
Лагранжа уравнения — 1) в гидромеханике уравнения движения жид кой среды, записанные в переменных Лагранжа, которыми являются координаты частиц среды. Из Л. у. определяется закон движения частиц среды в виде зависимостей координат от времени, а по ним… … Большая советская энциклопедия
Связи механические — ограничения, налагаемые на положение или движение механической системы. Обычно С. м. осуществляются с помощью каких нибудь тел. Примеры таких С. м.: поверхность, по которой скользит или катится тело; нить, на которой подвешен груз;… … Большая советская энциклопедия
Степеней свободы число — в механике, число независимых между собой возможных перемещений (См. Возможные перемещения) механической системы. С. с. ч. зависит от числа материальных частиц, образующих систему, и числа и характера наложенных на систему связей… … Большая советская энциклопедия
Голономная связь — Голономная связь механическая связь, налагающая ограничения только на положения (или перемещения) точек и тел системы. Математически выражается в виде равенства[1]: где qj обобщённые координаты, описывающие механическую систему, i=1…k … Википедия
голономные связи
Смотреть что такое «голономные связи» в других словарях:
голономные связи — Геометрические связи и дифференциальные связи, уравнения которых могут быть проинтегрированы. [Сборник рекомендуемых терминов. Выпуск 102. Теоретическая механика. Академия наук СССР. Комитет научно технической терминологии. 1984 г.] Тематики… … Справочник технического переводчика
ГОЛОНОМНЫЕ СИСТЕМЫ — механич. системы, в к рых все связи (см. СВЯЗИ МЕХАНИЧЕСКИЕ) явл. геометрическими (голономными), т. е. налагающими ограничения только на положения (или на перемещения за время движения) точек и тел системы, но не на величины их скоростей. Напр.,… … Физическая энциклопедия
СВЯЗИ МЕХАНИЧЕСКИЕ — ограничения, налагаемые на положение или движения механич. системы. Обычно С. м. осуществляются с помощью к. н. тел. Примеры таких С. м. поверхность, по к рой скользит или катится тело; нить, на к рой подвешен груз; шарниры, соединяющие звенья… … Физическая энциклопедия
Голономные системы — механические системы, в которых все связи (см. Связи механические) являются геометрическими (голономными), то есть налагающими ограничения только на положения (или перемещения за время движения) точек и тел системы, но не на величины их… … Большая советская энциклопедия
Связи механические — ограничения, налагаемые на положение или движение механической системы. Обычно С. м. осуществляются с помощью каких нибудь тел. Примеры таких С. м.: поверхность, по которой скользит или катится тело; нить, на которой подвешен груз;… … Большая советская энциклопедия
Голономная связь — Голономная связь механическая связь, налагающая ограничения только на положения (или перемещения) точек и тел системы. Математически выражается в виде равенства[1]: где qj обобщённые координаты, описывающие механическую систему, i=1…k … Википедия
голономная система — Механическая система, на которую наложены только голономные связи … Политехнический терминологический толковый словарь
голономная система — Механическая система, на которую наложены только голономные связи. [Сборник рекомендуемых терминов. Выпуск 102. Теоретическая механика. Академия наук СССР. Комитет научно технической терминологии. 1984 г.] Тематики теоретическая механика… … Справочник технического переводчика
Неголономные системы — механические системы, на которые, кроме геометрических, налагаются ещё кинематические связи, не сводящиеся к геометрическим и называемые неголономными (см. Голономные системы). Примером Н. с. является шар, катящийся без проскальзывания по … Большая советская энциклопедия