что такое главный вектор и главный момент плоской системы сил
Главный вектор и главный момент сил.
Связи и реакции связей.
Связь осуществляется при помощи гибкого тела, нити, каната или троса. Реакция такой связи приложена к телу в точке прикрепленной к нему нити. Перечислим некоторые типы связей, предполагая, что они изготовлены из абсолютно твердых материалов и трение в местах их соприкосновения с рассматриваемыми телами отсутствует.
2)Шарнирное соединение тел (сферический шарнир, шарнирная опора неподвижная).
Система сходящихся сил.
Системой сходящихся сил наз-ют такую систему сил, линии действия которых пересекаются в одной точке. Сходящиеся системы сил могут быть пространственными или плоскими, расположенные в одной плоскости.
Сходящиеся системы сил могут быть пространственными и плоскими, т.е. расположенными в одной плоскости.
Момент силы относительно точки и оси.
Моментом силы относительно точки называется алгебраическая величина, равная произведению модуля силы на кратчайшее расстояние от точки до линии действия силы.Численное значение момента силы F относительно точки О будем обозначать mo(F). Тогдаmo(F) = ±Fh.Моментом силы относительно оси называется алгебраическая величина момента проекции этой силы на плоскость, перпендикулярную к данной оси, относительно точки пересечения этой плоскости с осью. Момент силы F относительно оси считается положительным, если наблюдатель, смотрящий с положительного направления оси, видит поворот, совершаемый составляющей Fxy силы F, происходящим против хода часовой стрелки.Из определения момента силы относительно оси следует
9Приведение к равнодействующей силе сходящихся сил.
Сложить 2 силы или неск. сил – это значит найти их равнодействующую. Задача о сложении 2х сил, приложенных к тв. телу в одной точке решается на основании правила параллелограмма.
Системой сходящихся сил называют такую систему сил, линии действия которых пересекаются в одной точке
Сходящиеся системы сил могут быть пространственными и плоскими, т.е. расположенными в одной плоскости.
.величина равнодействующей определится следующей формулой:
Для определения направления равнодействующей к воспользуемся обычными выражениями для направляющих косинусов:
Пара сил и ее момент.
Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на тело. Действие пары сил на тело сводится к вращательному эффекту. Для характеристики этого эффекта вводится понятие момента пары.:Моментом пары называется величина, равная взятому с соответствующим знаком произведению модуля одной из сил пары на ее плечо. Для равновесия пар сил, действующих на твердое тело, необходимо и достаточно, чтобы модуль векторного момента эквивалентной пары сил был равен нулю или чтобы векторный многоугольник, построенный на векторных моментах заданных пар сил, был замкнут.Момент пары считается положительным, если пара стремится повернуть тело против хода часовой стрелки, и отрицательным – если по ходу часовой стрелки.
Главный вектор и главный момент сил.
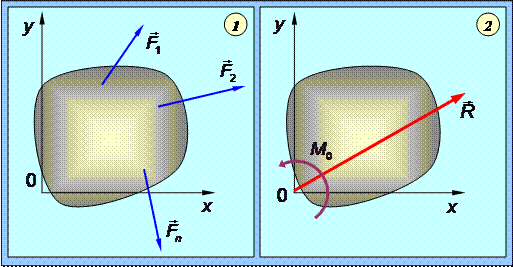
Главным вектором системы сил называют вектор, равный векторной сумме этих сил.
Главным моментом системы сил относительно точки O тела называют сумму векторных моментов всех сил системы относительно этой точки. Таким образом, основную теорему статики (теорему Пуансо) в краткой форме можно выразить так: Каждую систему сил можно привести к главному вектору и главному моменту относительно произвольного центра.
Тема 1.4. Система произвольно расположенных сил
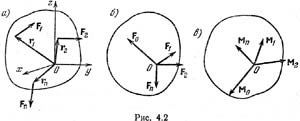
§1. Приведение пространственной системы сил к данному центру
Произвольной плоской системой сил называется совокупность сил, линии действия которых находятся в одной плоскости.
Теорема о параллельном переносе силы. Для переноса действующей на абсолютно твердое тело силы
из точки А (рис. 1, а) в точку О прикладываем в точке О силы и
Рис.1. Произвольной плоской системой сил
Рассмотрим теперь твердое тело, на которое действует какая угодно система сил
Чтобы сложить все полученные пары, надо геометрически сложить векторы моментов этих пар. В результате система пар заменится одной парой, момент которой или
называется главным моментом системы относительно этого центра.
Рис.2. Система сил
Таким образом мы доказали следующую теорему, любая система сил, действующих на абсолютно твердое тело, при приведении к произвольно взятому центру О заменяется одной силой
Векторы и обычно определяют аналитически, т.е. по их проекциям на оси координат.
Выражения для Rx, Ry, Rz нам известны. Проекции вектора на оси координат будем обозначать Mx, My, Mz. По теореме о проекциях суммы векторов на ось будет
Окончательно для определения проекций главного вектора и главного момента получаем формулы:
При этом главный вектор пространственной системы сил: R0 = ΣPi отличается от главного вектора плоской системы сил только наличием третьей компоненты, поэтому его модуль будет равен:
В зависимости от значений главного вектора и главного момента, а также от их взаимного расположения возможны следующие варианты приведения пространственной системы сил:
5) R0 ≠ 0, M0 ≠0 и главный вектор R0 неперпендикулярен главному моменту M0 — система эквивалентна скрещивающимся силам или динаме.
При этом скрещивающимися называются силы, которые непараллельны и не лежат в одной плоскости, а динамой называется система, состоящая из силы и пары сил, плоскость которой перпендикулярна этой силе.
Динама, приложенная к твердому телу, стремится вызвать его винтовое движение, которое представляет совокупность вращательного и поступательного движений.
Примечание: Для пространственной системы сил, как и для плоской, справедлива следующая Теорема Вариньона: Момент равнодействующей пространственной системы сил относительно произвольного центра (оси) равен геометрической (алгебраической) сумме моментов всех сил этой системы относительно данного центра (оси).
§2.Условия равновесия произвольной пространственной системы сил
Главный вектор и главный момент плоской системы сил
Главным вектором системы сил называется вектор R, равный векторной сумме этих сил:
Для плоской системы сил ее главный вектор лежит в плоскости действия этих сил.
Главным моментом системы сил относительно центра O называется вектор LO, равный сумме векторных моментов этих сил относительно точки О:
Вектор R не зависит от выбора центра О, а вектор LO при изменении положения центра О может в общем случае изменяться.
Для плоской системы сил вместо векторного главного момента используют понятие алгебраического главного момента. Алгебраическим главным моментомLO плоской системы сил относительно центра О, лежащего в плоскости действия сил, называют сумму алгебраических моментов этих сил относительно центра О.
Главный вектор и главный момент плоской системы сил обычно вычисляется аналитическими методами.
Главный вектор и главный момент плоской системы сил
В аналитическом методе для вычисления главного вектора и главного момента используются проекции сил Fix, Fiy и координаты xi, yi точек их приложения.
Модуль R главного вектора плоской системы сил и его направляющие косинусы ex, eу вычисляются по следующим формулам:
R = (Rх + Ry) 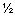
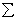
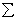
Алгебраический главный момент LO плоской системы сил относительно центра O ( начала координатных осей ) вычисляется по формуле:
Здесь во вторую сумму выделены алгебраические моменты Mk пар сил (Fk, F‘k).
В случаях, когда плечи hi всех сил определяются достатосно просто ( например, если силы параллельны координатным осям Ox и Oy ), величина LO может быть вычислена по формуле:
LO = 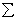
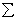
Лемма о параллельном переносе силы
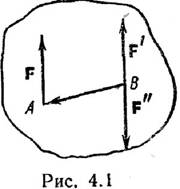
Докажем лемму: Сила, приложенная в какой-либо точке твердого тела, эквивалентна такой же силе, приложенной в любой другой точке этого тела, и паре сил, момент которой равен моменту данной силы относительно новой точки приложения. Пусть в точке А твердого тела приложена сила F (рис. 4.1). Приложим теперь в точке В тела систему двух сил F’ и F²-, эквивалентную нулю, причем выбираем F’=F (следовательно, F»=–F). Тогда сила F
0. Но, с другой стороны, система сил (F, F’, F») эквивалентна силе F’ и паре сил (F, F»); следовательно, сила F эквивалентна силе F’ и паре сил (F, F»). Момент пары (F, F») равен M=M(F,F»)=BAxF, т.е. равен моменту силы F относительно точки В M=MB(F). Таким образом, лемма о параллельном переносе силы доказана.
Основная теорема статики
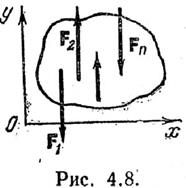
Пусть дана произвольная система сил (F1, F2. Fn). Сумму этих сил F=åFk называют главным вектором системы сил. Сумму моментов сил относительно какого-либо полюса называют главным моментом рассматриваемой системы сил относительно этого полюса.
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Главный вектор и главный момент плоской системы сил



Главным вектором системы сил называется вектор R, равный векторной сумме этих сил:
Для плоской системы сил ее главный вектор лежит в плоскости действия этих сил. Главным моментом системы сил относительно центра O называется вектор LO, равный сумме векторных моментов этих сил относительно точки О:
Вектор R не зависит от выбора центра О, а вектор LO при изменении положения центра О может в общем случае изменяться. Для плоской системы сил вместо векторного главного момента используют понятие алгебраического главного момента. Алгебраическим главным моментом LO плоской системы сил относительно центра О, лежащего в плоскости действия сил, называют сумму алгебраических моментов этих сил относительно центра О. Главный вектор и главный момент плоской системы сил обычно вычисляется аналитическими методами.
9 и 11)Условия равновесия плоской системы сил
Главный вектор и главный момент плоской системы сил



Рассмотрим плоскую систему сил ( 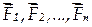
Главным вектором системы сил называется вектор 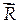
Для плоской системы сил её главный вектор лежит в плоскости действия этих сил.
Модуль R главного вектора плоской системы сил вычисляется по следующим формулам:
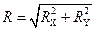 , , | (1.28) |
Главным алгебраическим моментом М0 плоской системы сил, называют сумму алгебраических моментов этих сил относительно некого центра (точки 0).
Величина M0 может быть вычислена по формуле:
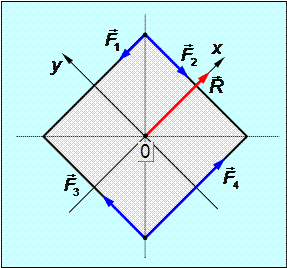
К вершинам квадрата со стороной a = 0.5(м) приложены силы: F1 = 4(Н); F2 = F3 = 8(Н); F4 = 12(Н). Определить главный вектор этой системы сил и её главный алгебраический момент относительно центра квадрата 0.
Решение. Введем координатную систему 0XY, оси которой параллельны сторонам квадрата.
Вычисление главного алгебраического момента M0 проведем с использованием плеч сил F1 и F4, равных половине длины стороны квадрата (a/2):
Таким образом, для заданной системы сил её главный вектор равен по модулю R = 8(Н) и направлен вдоль оси 0X, а её главный алгебраический момент M0 = 0.
Замечание. В случае, когда главный алгебраический момент M0 = 0, главный вектор R является равнодействующей силой заданной системы сил.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1. Что такое главный вектор системы сил?
2. Сформулируйте определение для главного момента системы сил.
3. Зависят ли значения главного вектора и главного момента системы сил от выбора центра?