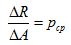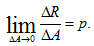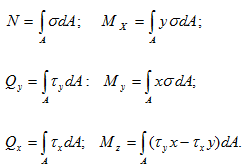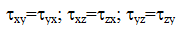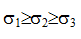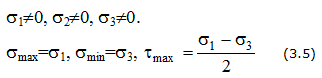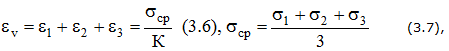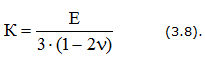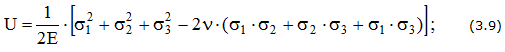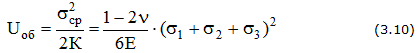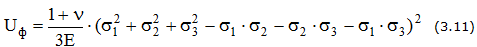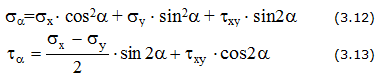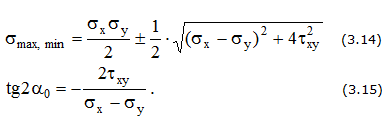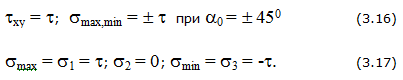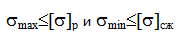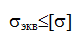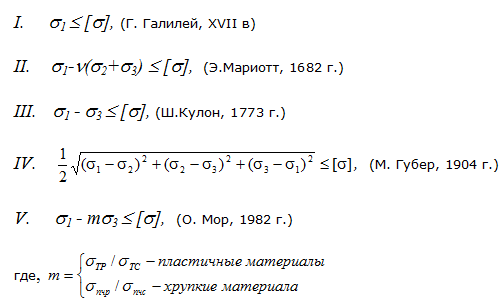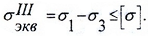что такое главные напряжения сопромат

iSopromat.ru

Рассмотрим понятие о напряженном состоянии в точке и гипотезы прочности. Связь между напряжениями и внутренними силами. Объемное, плоское и линейное напряженное состояния.

Понятие о напряжениях в точке

На основании допущения о сплошности тела можно считать, что внутренние силы непрерывно распределены по всему сечению.

Выделим в произвольной точке малую площадку ΔA, а равнодействующую внутренних сил на этой площадке обозначим ΔR. Отношение

представляет собой среднее напряжение на данной площадке.

Если площадку ΔA уменьшить, то в пределе получим полное напряжение в точке

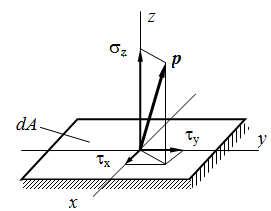
Полное напряжение р может быть разложено на три составляющие: по нормали к плоскости сечения и по двум осям в плоскости сечения. Проекция вектора полного напряжения р на нормаль обозначается через σ и называется нормальным напряжением.

Составляющие в плоскости сечения называются касательными напряжениями и обозначаются τ. В зависимости от расположения и наименования осей обозначения σ и τ снабжаются системой индексов.

Связь между напряжениями и внутренними силами

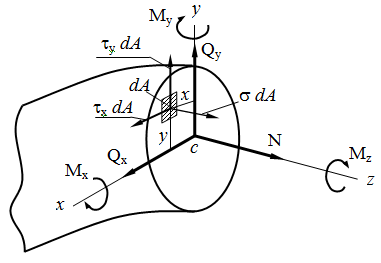
Установим связь между напряжениями и внутренними силами, возникающими в поперечном сечении стержня. Для этой цели выделим на сечении бесконечно малую площадку dA и приложим к ней элементарные силы σ dA, τ_x dA, τ_y dA.

Знак «А» у интеграла показывает, что интегрирование проводится по всей площади поперечного сечения. Приведённые формулы позволяют определить равнодействующие внутренних сил через напряжения, если известен закон распределения последних по сечению.

Обратную задачу с помощью только одних этих уравнений решить нельзя, так как одной и той же величине внутреннего усилия, например N, могут соответствовать различные законы распределения нормальных напряжений по сечению.

Одной из основных задач сопротивления материалов является задача об определении напряжений через равнодействующие внутренних сил. При этом оказывается, что решить эту задачу можно только, рассматривая параллельно с условиями равновесия и условия деформации бруса.

Объемное напряженное состояние

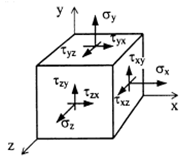
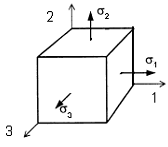
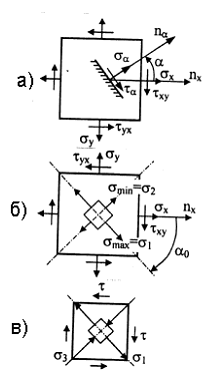
Совокупность напряжений, действующих по площадкам, проведенным через исследуемую точку, составляет напряженное состояние в рассматриваемой точке. На площадках общего положения действуют нормальные и касательные напряжения (рис. 3.1).

Значения касательных напряжений на взаимно перпендикулярных площадках подчиняются закону парности касательных напряжений:

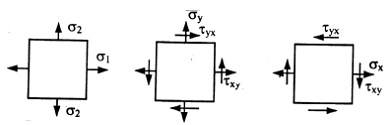
Площадки, на которых отсутствуют касательные напряжения, называются главными, а нормальные напряжения, действующие по этим площадкам, называются главными напряжениями (рис. 3.2).

Обозначение главных напряжений:

Напряженное состояние называется объемным или трехосным, если

Относительное изменение объема:

где К – модуль объемной упругости,

Удельная потенциальная энергия упругой деформации:

Плоское напряженное состояние

Напряженное состояние называется плоским или двухосным, если одно из главных напряжений равно нулю (рис. 3.3).

Напряжения на наклонной площадке (рис. 3.4,а)

Величина и направление главных напряжений (рис. 3.4,б)

Линейное напряженное состояние

Напряженное состояние называется линейным или одноосным, если два главных напряжения равны нулю.

Проверка прочности при линейном напряженном состоянии проводится по условию прочности:

В сложном напряженном состоянии проверку прочности проводят по гипотезам прочности по эквивалентному напряжению:

Величина σ_экв определяется, исходя из принятого критерия эквивалентности, лежащего в основе одной из гипотез разрушения или гипотез прочности, при котором сложное напряженное состояние заменяется эквивалентным ему растяжением или сжатием.

Гипотезы прочности

Существует 5 гипотез прочности:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

iSopromat.ru

Важнейшим критерием оценки прочности балок при изгибе являются напряжения.

Рассмотрим способы расчета напряжений при плоском поперечном изгибе балки

Расчет напряжений

Возникающий в поперечных сечениях при чистом прямом изгибе изгибающий момент M_x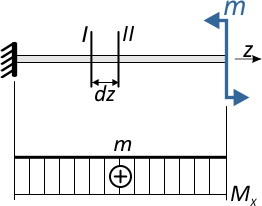

представляет собой равнодействующий момент внутренних нормальных сил, распределенных по сечению и вызывающих нормальные напряжения в точках сечения.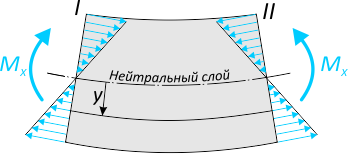

Закон распределения нормальных напряжений по высоте сечения выражается формулой: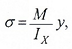

где:
M — изгибающий момент, действующий в рассматриваемом сечении относительно его нейтральной линии X;
I_x — осевой момент инерции поперечного сечения балки относительно нейтральной оси;
y – расстояние от нейтральной оси до точки, в которой определяется напряжение.

Нейтральная ось при изгибе проходит через центр тяжести поперечного сечения.

По вышеуказанной формуле, нормальные напряжения по высоте сечения изменяются по линейному закону.

Наибольшие значения имеют напряжения у верхнего и нижнего краев сечения.

Например, для симметричного относительно нейтральной оси сечения, где y₁=y₂=h/2: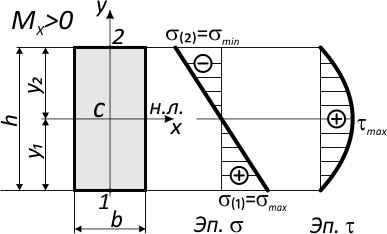

Напряжения в крайних точках по вертикали (точки 1 и 2) равны по величине, но противоположны по знаку.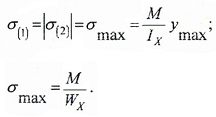

Для несимметричного сечения

напряжения определяются отдельно для нижней точки 1 и верхней точки 2: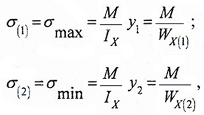

где: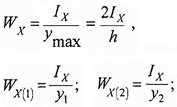

W_X — осевой момент сопротивления симметричного сечения;
W_X(1) и W_X(2) — осевые моменты сопротивления несимметричного сечения для нижних и верхних слоев балки.

Знаки нормальных напряжений при их расчете, рекомендуется определять по физическому смыслу в зависимости от того, растянуты или сжаты рассматриваемые слои балки.

Условия прочности при изгибе

Прочность по нормальным напряжениям

Условие прочности по нормальным напряжениям для балок из пластичного материала записывается в одной крайней точке.

В случае балки из хрупких материалов, которые, как известно, по-разному сопротивляются растяжению и сжатию – в двух крайних точках сечения.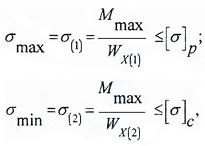

Здесь:
M_max — максимальное значение изгибающего момента, определяемого по эпюре M_x;
[ σ], [ σ]_р, [ σ]_с — допустимые значения напряжений для материала балки (для хрупких материалов – на растяжение (р) и сжатие (с)).

Для балки из хрупкого материала обычно применяют сечения, несимметричные относительно нейтральной оси. При этом сечения располагают таким образом, чтобы наиболее удаленная точка сечения размещалась в зоне сжатия, так как [ σ]_с>[ σ]_р.

В таких случаях, проверку прочности следует обязательно проводить в двух сечениях: с наибольшим положительным изгибающим моментом и с наибольшим по абсолютной величине (модулю) отрицательным значением изгибающего момента.

При расчете элементов конструкций, работающих на изгиб, с использованием вышеуказанных условий прочности решаются три типа задач:

Прочность по касательным напряжениям

В случае прямого поперечного изгиба в сечениях балки, кроме нормальных напряжений σ от изгибающего момента, возникают касательные напряжения τ от поперечной силы Q.

Закон распределения касательных напряжений по высоте сечения выражается формулой Д.И. Журавского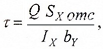

где
S_{x отс} — статический момент относительно нейтральной оси отсеченной части площади поперечного сечения балки, расположенной выше или ниже точки, в которой определяются касательные напряжения;
b_y — ширина поперечного сечения балки на уровне рассматриваемой точки, в которой рассчитывается величина касательных напряжений τ.

Условие прочности по касательным напряжениям записывается для сечения с максимальным значением поперечной силы Q_max:

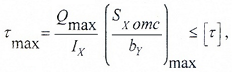
где [ τ] – допустимое значение касательных напряжений для материала балки.

Полная проверка прочности

Полную проверку прочности балки производят в следующей последовательности:

При анализе плоского напряженного состояния главные напряжения при изгибе, примут вид: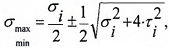

так как нормальные напряжения в поперечном направлении к оси балки принимаются равными нулю.

Проверка прочности осуществляется с помощью соответствующих гипотез прочности, например, гипотезы наибольших касательных напряжений:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Перевод. Примеры выполнения

Главные нормальные напряжения и направления в общем случае объёмного напряжённого состояния

Направляющие косинусы нормали на площадке общего положения удовлетворяют условию

Следовательно, возникает задача об отыскании условного экстремума напряжения при дополнительном условии (11.45).

Составим функцию Лагранжа:

Так как одновременно обратиться в нуль не могут, то система трёх однородных алгебраических уравнений (11.46) имеет заведомо отличные от нуля решения.

В этом случае определитель системы (11.46) должен равняться нулю:

Раскрывая определитель (11.48), приходим к кубическому уравнению

для определения трёх главных напряжений :

являются инвариантами тензора напряжений по отношению к преобразованиям координат x, y, z. Все три корня уравнения (11.49) позволяют найти направляющие косинусы главных направлений напряжённого состояния частицы тела. Поскольку из трёх уравнений (11.46) только два независимы, то беря, например, два первых уравнения и решая их совместно с (11.47) относительно по методу Крамера, получим:

В частном случае плоской задачи и определитель

(11.48) приводит к уравнению

откуда находим ранее полученную формулу

Полагая в (11.46) получим систему уравнений:

или, с учётом получаем

Пример 2. При растяжении стержня напряжения (рис. 11.19).

Расчет кулачкового механизма.

Рисунок 3. Кулачковый механизм.

2.2. Расчет профиля кулачка.

Для расчета профиля кулачка используем следующие данные:

— наибольший угол поворота коромысла – ;

-наибольшая сила давления коромысла на кулачок –5 Н;

Для построения профиля кулачка из конструктивных соображений выберем:

— расстояние между центром вращения кулачка и коромысла: L =106 (мм);

— длина коромысла: l =78 (мм);

-наименьший радиус кулачка: =46 (мм).

Рисунок 4. Профиль кулачка

Гипотезы пластичности при пластичном состоянии материала. Гипотеза наибольших касательных напряжений. Гипотеза энергии формоизменения и ее различные трактовки. Кручение стержней, сечение которых составлено из нескольких узких прямоугольников. Кручение тонкостенных стержней замкнутого профиля. Изгиб балок из разнородных материалов. Понятие об изгибе балок из материалов, не следующих закону Гука.
Прочность и разрушение материалов и конструкций

Источник

изучаем сопротивление материалов

Напряжения

Касательное напряжение, в свою очередь, может быть разложено на две составляющие, параллельные координатным осям x, y, связанным с поперечным сечением – [math]\tau_, \tau_[/math]. В названии касательного напряжения первый индекс указывает нормаль к площадке,второй индекс — направление касательного напряжения.

Тензор напряжений

Компоненты напряжений по трем перпендикулярным граням элемента образуют систему напряжений, описываемую специальной матрицей – тензором напряжений

$$ T _\sigma = \left[\matrix <
\sigma _x & \tau _ & \tau _ \\
\tau _ & \sigma _y & \tau _ \\ \tau _ & \tau _ & \sigma _z
>\right]$$

Здесь первый столбец представляет компоненты напряжений на площадках,
нормальных к оси x, второй и третий – к оси y и z соответственно.

При повороте осей координат, совпадающих с нормалями к граням выделенного
элемента, компоненты напряжений изменяются. Вращая выделенный элемент вокруг осей координат, можно найти такое положение элемента, при котором все касательные напряжения на гранях элемента равны нулю.

В каждой точке можно провести три взаимно-перпендикулярных главных площадки.

При повороте осей координат изменяются компоненты напряжений, но не меняется напряженно-деформированное состояние тела (НДС).

Связь внутренних усилий и напряжений

Внутренние усилия есть результат приведения к центру поперечного сечения внутренних сил, приложенных к элементарным площадкам. Напряжения – мера, характеризующая распределение внутренних сил по сечению.

Предположим, что нам известно напряжение в каждой элементарной площадке. Тогда можно записать:

Выполнив интегрирование по площади поперечного сечения получим:

То есть, каждое внутренне усилие есть суммарный результат действия напряжений по всему поперечному сечению тела.

1 Проекция вектора полного напряжения на нормаль к данной площадке называется нормальным напряжением и обознача­ется через σ_n.

Источник

Тема 2.1 Основные понятия и допущения

Элементы сооружений отличаются друг от друга формами, размерами, материалом, функциональным назначением, рядом специальных требований. При этом следует отметить, что все без исключения элементы как искусственного, так и естественного происхождения обладают такими свойствами, как прочность и жесткость, то есть способностью, не разрушаясь воспринимать различные нагрузки и сопротивляться изменению своих первоначальных форм и размеров, без чего не может нормально функционировать сооружение. Цель расчетов в сопротивлении материалов – создание прочных, устойчивых, обладающих достаточной жесткостью, долговечностью и вместе с тем экономичных элементов сооружений

Например, конструкции стропильной фермы, междуэтажных перекрытий зданий должны выдерживать нагрузки от атмосферных воздействий, оборудования и людей и обладать достаточной жесткостью, обеспечивающей ограничение прогибов для создания нормальных условий функционирования сооружения.

Рис. 1. Характер деформирования и разрушения стержня под нагрузкой:

а) – элемент до нагружения; б) – деформация стержня при изгибе; в) – вид излома элемента при изгибе; г) – изгиб стержня при сжатии

Прочностные и жесткостные качества элементов сооружений зависят от многих факторов: материала, размеров, характера возникающих деформаций и др. Металлические конструкции обладают большей прочностью и жесткостью, чем аналогичные деревянные конструкции. Стержень из одного и того же материала, имеющий большие поперечные размеры, более прочный и жесткий, при этом его легче разрушить, изгибая, чем растягивая. Тонкий стержень при его сжатии разрушается в результате выпучивания в поперечном направлении, в то же время это явление отсутствует при продольном растяжении и для разрушения стержня требуется значительно большая нагрузка.

Например, возьмем деревянный брусок (рис.1, а). Начнем сгибать стержень. Чем сильнее мы будем прикладывать усилия, тем больше он изогнется (рис.1 б), и при какой то величине усилий сломается (рис.1, в). Подведя итог можно утверждать, что всякое реальное тело под воздействием сил меняет свою форму и размеры, т. е. деформируется. Деформации обуславливают появление внутри элемента сил сопротивления. Если внешние силы больше сил сопротивления, происходит разрушение элемента сооружения.

При возрастании нагрузки выше определенных значений в теле наряду с упругими будут возникать деформации не исчезающие после снятия нагрузки. Такие деформации называются остаточными. Возникновение остаточных деформаций, наравне с разрушением связано с нарушением нормальной работы конструкции и, как правило, недопустимо.

Способность конструкции воспринимать заданную нагрузку, не разрушаясь и без остаточных деформаций, называют прочностью.

Все элементы сооружения, из каких бы материалов они ни были изготовлены, под нагрузкой деформируются. Однако значительные деформации могут мешать нормальной эксплуатации сооружения.

Способность сооружений и ее частей под нагрузкой сохранять свои размеры и форму в установленных нормами пределах называется жесткостью.

Рассмотрим еще один пример. Будем сжимать тонкий и длинный стержень (тот же деревянный брусок). Уже при незначительной силе стержень изогнется, как показано на рис.1, г. В этом случае первоначальная форма прямолинейная форма равновесия стержня становится неустойчивой.

Способность конструкции, и ее частей, сохранять под нагрузкой первоначальную форму упругого равновесия называется устойчивостью. Обычно потеря устойчивости сопровождается мгновенным изменением формы элемента и разрушением конструкции.

Методами сопротивления материалов выполняются расчеты, на основании кото­рых определяются необходимые размеры деталей машин и конструкций инженерных сооружений. Любая конструкция должна обладать надежностью при эксплуатации и быть экономичной.

Надежность – свойство конструкции выполнять заданные функции, сохраняя свои эксплуатационные показатели в определенных нормативных пределах в течение требуемого промежутка времени.

В сопротивлении материалов широко применяются методы теоретической механики и математического анализа, используются данные из разделов физики, изучающих свойства различных материалов, материаловедения и других наук. К тому же сопротивление материалов является наукой экспериментально-теоретической, так как она широко использует опытные данные и теоретические исследования.

ЗАДАНИЕ:

Что изучает раздел «Сопротивление материалов»?

Выписать определения: прочность, жесткость, устойчивость, надежность и экономичность.

§2. Реальный объект и расчетная схема

При выборе расчетной схемы вводятся упрощения (схематизация) реального объекта, т.е. отбросить все те факторы, которые не могут сколько-нибудь заметным образом повлиять на работу системы в целом.

Такого рода упрощения задачи совершенно необходимы, так как решение с полным учетом всех свойств реального объекта является принципиально невозможным в силу их очевидной неисчерпаемости.

Основным упрощающим приемом в сопротивлении материалов является приведение геометрической формы тела к схемам бруса (стержня), оболочки или пластины. Как известно, любое тело в пространстве характеризуется тремя измерениями.

Рис. 2. Прямой брус (стержень) постоянного сечения

ЗАДАНИЕ:

У казать чем отличается расчетная схема от реального объекта.

Начертить стержень, изобразив его ось и поперечное сечение, записать определение стержня.

§3. Связи и опорные устройства

Для соединения отдельных частей конструкции между собой и передачи внешней нагрузки на основание на нее накладываются связи , ограничивающие перемещения тех точек сооружения, к которым они приложены. Связи могут ограничивать либо повороты точек сооружения, либо их линейные смещения, либо и то и другое.

Основным видом связей в расчетной схеме является шарнирная связь.

Все опорные связи условно делятся на три основных типа:

— Подвижная шарнирная опора (рис.3, а). Такая опора не препятствует вращению конца бруса и его перемещению вдоль плоскости качения. В ней может возникать только одна реакция, которая перпендикулярна плоскости качения и проходит через ось катка (R).

— Жесткая заделка или защемление (рис.3, в). Такое закрепление не допускает ни линейных, ни угловых перемещений опорного сечения. В этой опоре в общем случае может возникать реакция, которую обычно раскладывают на две составляющие (H и R) и момент защемления (М).

При рассмотрении реального объекта в число внешних сил включаются не только заданные нагрузки, но и реакции связей (опор), дополняющие систему сил до равновесного состояния.

§4. Внешние и внутренние силы. Метод сечений

Поверхностные силы приложены к участкам поверхности и являются результатом непосредственного контактного взаимодействия рас­сматриваемого объекта с окружающими телами (давление ветра, воды на стенку).

В зависимости от соотношения площади приложения нагрузки и общей площади поверхности рассматриваемого тела, поверхностные нагрузки подразделяются на сосредоточенные и распределенные.

Динамические нагрузки также подразделяются на периодические и случайные нагрузки. К случайным нагрузкам относятся нагрузки, действующие на детали автомобилей, тракторов, станков, а также нагрузки, действующие на сооружения (дома, мачты, краны и т.п.) от давления ветра, снега и т.п.

Временная нагрузка может сохранять более или менее постоянную величину в течение всего периода ее действия, а может непрерывно изменяться по некоторому закону; в последнем случае она называется переменной нагрузкой.

По отношению к выбранному материальному телу (элементу конструкции) все действующие силы подразделяются на внешние и внутренние силы. Под внешними силами (нагрузками) понимаются силы взаимодействия данного материального тела со всеми другими окружающими его телами.

Взаимодействие между частями рассматриваемого тела характеризуется внутренними силами , которые возникают внутри тела под действием внешних нагрузок и определяются силами межмолекулярного воздействия. Эти силы сопротивляются стремлению внешних сил разрушить элемент конструкции, изменить его форму, отделить одну часть от другой. Вообще внутренние силы возникают между всеми смежными частицами тела при нагружении.

ЗАДАНИЕ:

Составить таблицу «Виды нагрузок», в таблице дать характеристику каждому виду нагрузки.

Рис.4. Внутренние силовые факторы, возникающие при действии нагрузки

В зависимости от вида внутренних силовых факторов, возникающих в сечении, различают различные следующие виды нагружения бруса:

— Растяжение или сжатие. Действует только продольная сила N.

— Кручение. Действует только крутящий момент T.

— Сдвиг. Действует только поперечная сила Q x или Q y

— Изгиб. Действует только изгибающий момент M x или M y (чистый изгиб), при действии изгибающего момента и поперечной силы (поперечный изгиб).

— Сложное сопротивление. Одновременное действие нескольких силовых факторов. Например, M x и T, M и N.

Итак, внутренние усилия в сечении есть функции параметров, определяющих положение сечения в теле, и нагрузок по одну сторону от сечения. Эти функции могут быть представлены аналитически или графически. График, показывающий изменение внутреннего усилия в зависимости от положения сечения, называется эпюрой . Ординаты усилий в определенном масштабе откладывают от линии, соответствующей оси бруса.

ЗАДАНИЕ:

Начертить внутренние силовые факторы стержня(рис. 4), дать пояснение каждому символу на этой схеме и указать вид нагружения при котором возникают N , Q y и Q z , Т , M z и М у .

§5. Допущения, применяемые в сопротивлении материалов

Для построения теории сопротивления материалов принимают некоторые понятия и допущения относительно структуры и свойств материалов, а также о характере деформаций. Приведем основные из них.

1. В сопротивлении материалов принято рассматривать все материалы как однородную сплошную среду, независимо от их микроструктуры. Под однородностью материала понимают независимость его свойств от величины выделенного из тела объема. И хотя в действительности реальный материал, как правило, неоднороден (уже в силу его молекулярного строения), тем не менее, указанная особенность не является существенной, поскольку в сопротивлении материалов рассматриваются конструкции, размеры которых существенно превышают не только межатомные расстояния, но и размеры кристаллических зерен.

Металлы и сплавы, как правило, изотропны, так как большинство металлов имеет мелкозернистую структуру. Благодаря большому количеству кристаллов свойства материалов выравниваются в различных направлениях и можно считать эти материалы практически изотропными. В настоящее время широкое распространение получили анизотропные композиционные материалы, состоящие из двух компонентов – наполнителя и связующего. Наполнитель состоит из уложенных в определенном порядке высокопрочных нитей – матрицы, что и определяет значительную анизотропию композита. Композиционные материалы имеют высокую прочность при значительно меньшем, чем металлы весе.

Результат воздействия на тело системы сил равен сумме результатов воздействия тех же сил, прилагаемых к телу последовательно и в любом порядке (рис. 6). Под словами «результат воздействия» следует понимать – деформации, внутренние силы и перемещения отдельных точек.

Источник