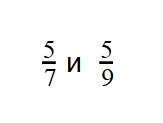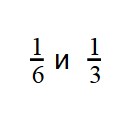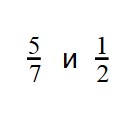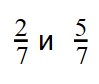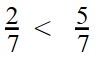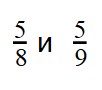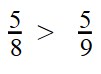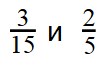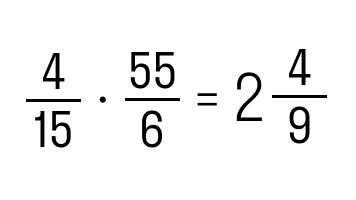что делать если в смешанной дроби числитель больше знаменателя
Неправильная дробь
Неправильная дробь– это та, у которой значение числителя больше величины знаменателя. Если же числа в числителе и знаменателе одинаковые, такую дробь также называют неправильной.
Примеры неправильных дробей
Зачастую неправильную дробь для удобства и более привычного понимания представляют в виде смешанной дроби, т.е. такой, у которой есть целая часть и правильная дробь (такая, у которой числитель меньше знаменателя).
Приведём некоторые примеры неправильных и смешанных дробей:
это неправильные дроби, потому как их числитель больше знаменателя либо равен ему, т.е. итоговое число, получаемое делением числителя на знаменатель, будет больше либо равно 1;
это смешанные дроби, потому как каждую из них составляет целая часть и правильная дробь, т.е. при переводе заданной неправильной дроби в такую в итоге получаем какое–то целое число и некий остаток в виде дроби, числитель которой меньше знаменателя.
Перевести смешанную дробь 2 2 /3 в неправильную.
Для этого сначала умножаем целую часть на знаменатель, а полученное значение добавляем к величине числителя; при этом в знаменателе итоговой неправильной дроби оставляем знаменатель смешанной.
Находим, что неправильная дробь из заданной смешанной следующая:
Проверим результат. Введём в соответствующее поле нашего КАЛЬКУЛЯТОРА НЕПРАВИЛЬНОЙ ДРОБИ заданные значения и получим искомый ответ 8 /3
Перевести смешанную дробь в неправильную.3 8 /9
Повторяем предложенные действия из примера 1 и находим, что неправильная дробь из заданной смешанной следующая:
Проверим результат в нашем калькуляторе неправильных дробей; получили 35 /9
А в качестве домашнего задания предлагаем вам определить следующее: является ли 2 3 /3 смешанной дробью?
Сравнение дробей, как правильно
Сравнение дробей с одинаковыми знаменателями
Как и при любом другом сравнении, суть сравнения дробей — в том, чтобы определить меньшую и большую дроби.
Нет ситуации более благоприятной для сравнения, чем дроби с одинаковыми знаменателями. Если вся разница между дробями только в числителях, пользуемся следующим правилом:
Из двух дробей с одинаковыми знаменателями больше дробь с большим числителем. А меньше будет та дробь, числитель которой меньше.
А теперь на примерах.
Пример 1. Сравните дроби:
Пример 3. Сравните дроби:
Как видите, нет ничего сложного в сравнении дробей, если знаменатели равны. Вся задача заключается в том, чтобы определить больший и меньший знаменатель.
Давайте разберем наглядный пример сравнения дробей:
Допустим, в торте 6 кусков. Если от целого торта отрезать один кусок — в торте останется 5 кусков.
Понять, что целый торт больше, чем торт без одного куска, можно и без сравнения дробей. Но это же самое правило можно применить и при менее очевидных сравнениях, которые часто встречаются в повседневной жизни.
Сравнение дробей с одинаковыми числителями
Вы уже разобрались со сравнением дробей с одинаковыми знаменателями. Теперь задача чуть усложняется — научимся сравнивать дроби с разными знаменателями, но с одинаковыми числителями.
Если у двух дробей одинаковые числители, то больше будет та дробь, чей знаменатель меньше. А меньше будет дробь с большим знаменателем.
А теперь наши любимые примеры. Погнали!
Пример 1. Сравните дроби:
Пример 3. Сравните дроби:
Сравнение дробей с разными числителями и разными знаменателями
Нет ничего хитрого в сравнении дробей с одинаковыми числителями или знаменателями. Чуть больше усилий потребуется при сравнении дробей, в которых нет ничего одинакового.
Сначала вспомним, как привести дроби к общему знаменателю.
Рассмотрим пример дробей с разными знаменателями.
Давайте потренируемся в сравнении дробей.
Пример 1. Сравните дроби:
При сравнении неправильных дробей, помните, что неправильная дробь всегда больше правильной.
Пример 2: Сравните дроби:
Вычитание смешанных чисел
Вычитание проходит гладко, когда уменьшаемое больше вычитаемого.
В случае, если вычитаемое больше уменьшаемого, разность оказывается отрицательной. В этом нет ничего страшного. Но математика в 5 классе — «положительная», поэтому научимся находить разность смешанных чисел, не скатываясь «в минусы».
При вычитании дробей действует тот же самый принцип: вычитаемое должно быть больше уменьшаемого. Вот здесь то вам и пригодится навык сравнивать дроби.
Пример 1. Найдите разность:
Вычитаемая дробь меньше уменьшаемой
Пример 2.Найдите разность:
Если знаменатели одинаковые — больше та дробь, числитель которой больше.
Примеры для самопроверки
Теория — это, конечно, хорошо. Но без практики — никуда. Пора потренироваться в решении примеров и закрепить тему сравнения дробей.
Пример 1. Сравните дроби:
Ответ: по правилу сравнения дробей с одинаковыми знаменателями, больше та дробь, у которой числитель больше. Это значит, что
Пример 2. Сравните дроби:
Ответ: по правилу сравнения дробей с разными знаменателями и одинаковыми числителями, больше та дробь, чей знаменатель меньше. Это значит, что
Пример 3. Сравните дроби:
Ответ: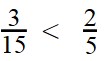
Как перевести смешанную дробь в неправильную и наоборот
Объяснения с примерами
Как перевести смешанную дробь в неправильную
Смешанная дробь — это запись целого числа с обыкновенной дробью.
Читается 5 целых три восьмых.
Чтобы нагляднее себе представить, можно мысленно добавлять знак «+» между целым числом и обыкновенной дробью. И это не будет ошибкой, так как знак «плюс» для упрощения записи опускается.
Эта запись означает 5 целых пирогов и 3 восьмых пирога.
5 площадей определенных размеров и 3 восьмых данной площади.
Неправильная дробь — эта та, у которой числитель больше знаменателя. Соответственно, из неё можно выделить 1 целое число или больше. Так как любая неправильная дробь больше единицы.
Можно сделать действие и наоборот — превратить смешанное число в неправильную дробь.
Чтобы перевести смешанное число в неправильную дробь нужно целое число умножить на знаменатель и прибавить числитель. Полученное значение записываем в числитель. Знаменатель оставляем без изменений.
Объяснение почему именно так мы переводим:
Целое число мы можем записать дробью, как сорок восьмых (40: 8 = 5). Не забывайте, что дробь — это деление. Число 40 мы получаем умножением целого числа на знаменатель. Теперь нам осталось сложить две дроби с одинаковыми знаменателями.
Примеры для перевода смешанных дробей в неправильные
Как перевести неправильную дробь в смешанную
Как мы уже говорили, неправильная дробь всегда больше единицы.
Чтобы перевести неправильную дробь в смешанную нужно начать делить числитель на знаменатель до целых. Полученное целое число пишем перед дробью, остаток деления — в числитель. Знаменатель остаётся без изменения.
Схема для запоминания:
Примеры
Как перевести неправильную дробь в правильную
Смешанную дробь иногда называют правильной, поэтому объяснение перевода будет являться дублированием предыдущего абзаца. Если у вас остались вопросы, то смотрите разбор в видео:
Сложение дробей: теория и практика
Понятие дроби
Дробь — одна из форм представления числа в математике. Это запись, в которой a и b являются числами или выражениями. Существует два формата записи:
Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между ними означает деление.
Дроби бывают двух видов:
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.
Неправильной — ту, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как пять целых одна четвертая, а записывается — 5 1\4.
Основные свойства дробей
1. Дробь не имеет значения, при условии, если делитель равен нулю.
2. Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
3. Равными называются такие a/b и c/d, если:
4. Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Как плюсовать дроби
Сложение — это арифметическое действие, в результате которого получается новое число. Оно содержит в себе сумму заданных чисел.
Свойства сложения
Давайте рассмотрим несколько вариантов сложения обыкновенных дробей.
Сложение дробей с одинаковыми знаменателями
Чтобы получить результат суммы двух дробей с равными знаменателями, нужно сложить числители исходных дробей, а знаменатель оставить прежним.
Не забудьте проверить, можно ли сократить дробь.
Сложение дробей с разными знаменателями
Как складывать дроби с разными знаменателями — для этого нужно найти наименьший общий знаменатель (далее — НОЗ), а затем воспользоваться предыдущим правилом. Вот, что делать:
1. Найдем наименьшее общее кратное (далее — НОК) для определения единого делителя.
Для этого записываем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.
НОК (15, 18) = 3 * 2 * 3 * 5 = 90
2. Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:
Полученные числа записываем справа сверху над числителем.
3. Воспользуемся одним из основных свойств дробей: перемножим делимое и делитель на дополнительный множитель. После умножения делитель должен быть равен наименьшему общему кратному, которое мы ранее высчитывали. Затем можно перейти к сложению.
4. Проверим полученный результат:
Еще раз ход решения одной строкой:
Сложение смешанных чисел
Сложение смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:
1. Сложить целые части.
2. Сложить дробные части.
Если знаменатели разные, воспользуемся знаниями из предыдущего примера и приведем к общему.
3. Суммируем полученные результаты.
Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.
Если урок в самом разгаре и посчитать нужно быстро — можно воспользоваться онлайн-калькулятором. Вот несколько подходящих:
Прибавление и вычитание дробей — смежные темы: принципы и закономерности очень похожи. Чтобы закрепить знания, нужно решать примеры сложения дробей, как можно чаще.
Умножение дробей: теория и практика
Понятие дроби
Дробь — одна из форм представления числа в математике. Это запись, в которой a и b являются числами или выражениями. Существует два формата записи:
Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление — в 5 классе уже это знают.
Дроби могут быть двух видов:
Дробь называют правильной, когда ее числитель меньше знаменателя:
Неправильной — ту, у которой числитель больше знаменателя или равен ему:
Такое число называют смешанным, читают как «пять целых одна четвертая», а записывают так: 5 1\4.
Основные правила дробей
Умножение дробных чисел
Рассмотрим несколько вариантов умножения обыкновенных дробей.
Как умножить дробь на дробь
Числитель равен произведению числителей обеих дробей, а знаменатель равен произведению знаменателей:
Важно проверить возможность сокращения — так решать будет легче:
Как умножить смешанные дроби
Преобразовать смешанные числа в неправильные, перемножить числители и знаменатели, при необходимости сократить и перевести в смешанную дробь.
Как умножить дробь на натуральное число
Метод 1. Числитель умножить на натуральное число, а знаменатель оставить без изменения. Если в результате произведения получилась неправильная дробь, нужно выделить целую часть, то есть превратить неправильную в смешанную.
Метод 2. Знаменатель разделить на натуральное число, а числитель оставить прежним.
Этот способ будет удобнее предыдущего, если знаменатель делится на натуральное число без остатка.
Решение задач
Ребятам в 5 и 6 классе нужно практиковаться как можно чаще, чтобы решать такие примеры быстро и легко.
Задание 1. Выполнить умножение 2/17 на 5.
Как решаем: перемножим делимое и натуральное число.
Ответ:
Задание 2. Выполнить умножение 4/15 и 55/6.
Как решаем:
Ответ:
Задание 3. Выполнить умножение одной целой трех седьмых на шесть.
Как решаем:
Ответ:
Онлайн-курсы по математике для детей и подростков — прекрасный способ разобраться в новом материале и закрепить его на практике.