что делать если у логарифмов разные основания

Что делать если у логарифмов разные основания

Логарифмическое уравнение.

Определение:

Логарифмическое уравнение – это уравнение вида

Уравнения, сводящиеся к этому виду, также называются логарифмическими уравнениями.

Правило:

Пояснение:

В процессе решения логарифмического уравнения log_a b(x) = log_a c(x) надо просто убрать значки логарифмов и решить получившееся упрощенное уравнение b(x) = c(x).

Важно знать:

1) Если в уравнении разные основания, то логарифмы убирать нельзя. В левой и правой частях уравнения должны быть одинаковые основания. Возьмем для примера уравнение:

Здесь слева и справа одинаковое основание 5. Значит, можно убрать значки логарифмов и привести уравнение к более простому и понятному виду:

Если основания неодинаковы, необходимо преобразовать одно из выражений так, чтобы основания стали одинаковыми – и только после этого уравнение можно потенцировать.

2) Даже если основания слева и справа одинаковые, но в уравнении есть коэффициент, то в этом случае тоже убирать логарифмы нельзя. К примеру, нельзя потенцировать уравнение такого типа:

Мешает коэффициент 3 в левой части. Поэтому уравнение надо преобразовать так, чтобы коэффициент исчез. В нашем уравнении, применив одно из свойств логарифмов log_a b n = n · log_a b, мы можем преобразовать выражение слева:

Тогда наше уравнение обретает другой вид:

Теперь мы имеем одинаковые основания (число 2), и уравнение без коэффициентов. Значит, уже легко можем убрать значки логарифмов:

И такое уравнение решать намного проще:

3) Даже при одинаковых основаниях и отсутствии коэффициентов нельзя потенцировать уравнение, если в какой-то из его частей больше одного логарифма. Например, нельзя убирать логарифмы в уравнении

В левой части два логарифма. Надо сначала преобразовать ее. Для этого воспользуемся еще одним правилом: сумма логарифмов равна логарифму произведения. Итак, преобразовываем левую часть уравнения:

У нас получилось выражение с одним логарифмом. А наше уравнение принимает новый вид:

И мы уже можем убрать значки логарифмов:

Решаем это простое уравнение:

1) Поскольку основания в левой и правой частях одинаковые (равны 3), то мы можем освободиться от знаков логарифмов и прийти к уравнению вида b(x) = c(x):

2) Приравниваем уравнение к нулю и получаем квадратное уравнение:

Решив квадратное уравнение, находим его корни:

3) Проверим, при каком из двух значений х уравнение имеет смысл.

Мы уже знаем, что логарифмическое уравнение равносильно уравнению b(x) = c(x) только в том случае, если b(x) > 0 и c(x) > 0. Следовательно, выводим два неравенства:

При х = 4 неравенства неверны. Значит, 4 не является решением уравнения.

При х = –3 неравенства верны. Значит, 3 является единственным решением уравнения.

Логарифмическое неравенство.

Определение:

Логарифмическое неравенство – это неравенство вида

Неравенства, сводящиеся к этому виду, также называются логарифмическими неравенствами.

Правило:

Для решения логарифмических неравенств log_a b(x) > log_a c(x) обычно применяют систему неравенств следующего вида:

1) В основании обеих частей уравнения – одно и то же число 3. Значит, можем убрать значки логарифмов. Поскольку 3 больше 1, то, следуя правилу, составляем следующую систему неравенств:

Решаем неравенства и получаем:

Мы видим, что х больше не только двух, но и больше шести. Значит, неравенство x > 2 мы уже в расчет не берем: если х больше 6, то естественно и больше 2. Таким образом, для нас важны только два других неравенства, согласно которым х больше 6, но меньше 14. Это и есть ответ :

Источник

Логарифмическое уравнение: решение на примерах

Как решить логарифмическое уравнение? Этим вопросом задаются многие школьники, особенно в преддверии сдачи ЕГЭ по математике. Ведь в задании С1 профильного ЕГЭ могут встретиться именно логарифмические уравнения.

Уравнение, в котором неизвестное находится внутри логарифмов, называется логарифмическим. Причем неизвестное может находится как в аргументе логарифма, так и в его основании.

Способов решения таких уравнений существует несколько. В этой статье мы разберем способ, который легко понять и запомнить.

Как решать уравнения с логарифмами: 2 способа с примерами

Решить логарифмическое уравнение можно разными способами. Чаще всего в школе учат решать логарифмическое уравнение с помощью определения логарифма. То есть мы имеем уравнение вида:Вспоминаем определение логарифма и получаем следующее:Таким образом мы получаем простое уравнение, которое сможем легко решить.

При решении логарифмических уравнений важно помнить об области определения логарифма, т.к. аргумент f(x) должен быть больше ноля. Поэтому после решения логарифмического уравнения мы всегда делаем проверку!

Давайте посмотрим, как это работает на примере:

Воспользуемся определением логарифма и получим:

Теперь перед нами простейшее уравнение, решить которое не составит труда:

Сделаем проверку. Подставим найденный Х в исходное уравнение:Так как 3 2 = 9, то последнее выражение верно. Следовательно, х = 3 является корнем уравнения.

Основной минус данного метода решения логарифмических уравнений в том, что многие ребята путают, что именно нужно возводить в степень. То есть при преобразовании log_af(x) = b, многие возводят не a в степень b, а наоборот b в степень a. Такая досадная ошибка может лишить вас драгоценных баллов на ЕГЭ.

Поэтому мы покажем еще один способ решения логарифмических уравнений.

Чтобы решить логарифмическое уравнение, нам нужно привести его к такому виду, когда и в правой, и в левой части уравнения будут стоять логарифмы с одинаковыми основаниями. Это выглядит вот так:

Когда уравнение приведено к такому виду, то мы можем «зачеркнуть» логарифмы и решить простое уравнение. Давайте разбираться на примере.

Решим еще раз то же самое уравнение, но теперь этим способом:В левой части у нас логарифм с основанием 2. Следовательно, правую часть логарифма нам нужно преобразовать так, чтобы она тоже содержала логарифм с основанием 2.

Для этого вспоминаем свойства логарифмов. Первое свойство, которое нам здесь понадобится – это логарифмическая единица. Напомним его:То есть в нашем случае:Возьмем правую часть нашего уравнения и начнем ее преобразовывать:Теперь нам нужно 2 тоже внести в логарифмическое выражение. Для этого вспоминаем еще одно свойство логарифма:

Воспользуемся этим свойством в нашем случае, получим:Мы преобразовали правую часть нашего уравнения в тот вид, который нам был нужен и получили:Теперь в левой и в правой частях уравнения у нас стоят логарифмы с одинаковыми основаниями, поэтому мы можем их зачеркнуть. В результате, получим такое уравнение:

Да, действий в этом способе больше, чем при решении с помощью определения логарифма. Но все действия логичны и последовательны, в результате чего шансов ошибиться меньше. К тому же данный способ дает больше возможностей для решения более сложных логарифмических уравнений.

Разберем другой пример:Итак, как и в предыдущем примере применяем свойства логарифмов и преобразовываем правую часть уравнения следующим образом:После преобразования правой части наше уравнение принимает следующий вид:Теперь можно зачеркнуть логарифмы и тогда получим:Вспоминаем свойства степеней:

Теперь делаем проверку:то последнее выражение верно. Следовательно, х = 3 является корнем уравнения.

Еще один пример решения логарифмического уравнения:Преобразуем сначала левую часть нашего уравнения. Здесь мы видим сумму логарифмов с одинаковыми основаниями. Воспользуемся свойством суммы логарифмов и получим:Теперь преобразуем правую часть уравнения:Выполнив преобразования правой и левой частей уравнения, мы получили:Теперь мы можем зачеркнуть логарифмы:

Решим данное квадратное уравнение, найдем дискриминант:

Сделаем проверку, подставим х₁ = 1 в исходное уравнение:Верно, следовательно, х₁ = 1 является корнем уравнения.

Пример решения логарифмического уравнения с разными основаниями

Выше мы решали логарифмические уравнения, в которых участвовали логарифмы с одинаковыми основаниями. А что же делать, если основания у логарифмов разные? Например,

Правильно, нужно привести логарифмы в правой и левой части к одному основанию!

Итак, разберем наш пример:Преобразуем правую часть нашего уравнения:

Тогда получим:Вот теперь в правой и левой части уравнения у нас стоят логарифмы с одинаковыми основаниями и мы можем их зачеркнуть:Делаем проверку:Если мы преобразуем правую часть, воспользовавшись свойствами логарифма, то получим:Верно, следовательно, х = 4 является корнем уравнения.

Пример решения логарифмического уравнения с переменными основаниями

Выше мы разобрали примеры решения логарифмических уравнений, основания которых были постоянными, т.е. определенным значением – 2, 3, ½ … Но в основании логарифма может содержаться Х, тогда такое основание будет называться переменным. Например, log_x+1(х 2 +5х-5) = 2. Мы видим, что основание логарифма в данном уравнении – х+1. Как же решать уравнение такого вида? Решать мы его будем по тому же принципу, что и предыдущие. Т.е. мы будем преобразовывать наше уравнение таким образом, чтобы слева и справа были логарифмы с одинаковым основанием.Преобразуем правую часть уравнения:Теперь логарифм в правой части уравнения имеет такое же основание, как и логарифм в левой части:Теперь мы можем зачеркнуть логарифмы:Но данное уравнение неравносильно исходному уравнению, так как не учтена область определения. Запишем все требования, относящиеся к логарифму:

1. Аргумент логарифма должен быть больше ноля, следовательно:

2. Основание логарифма должно быть больше 0 и не должно равняться единице, следовательно:

Сведем все требования в систему:

Для полной уверенности можем выполнить проверку, подставим х = 2 в исходное уравнение:

Т.к. 3 2 =9, то последнее выражение верно.

Как сделать проверку

Еще раз обращаем ваше внимание, что при решении логарифмических уравнений необходимо учитывать область допустимых значений. Так, основание логарифма должно быть больше ноля и не должно равняться единице. А его аргумент должен быть положительным, т.е. больше ноля.

Если наше уравнение имеет вид log_a (f(x)) = log_a (g(x)), то должны выполняться следующие ограничения:

После решения логарифмического уравнения нужно обязательно сделать проверку. Для этого вам необходимо подставить получившееся значения в исходное уравнение и посчитать его. Времени это займет немного, зато позволит не записать в ответ посторонние корни. Ведь так обидно правильно решить уравнение и при этом неправильно записать ответ!

Итак, теперь вы знаете, как решить логарифмическое уравнение с помощью определения логарифма и с помощью преобразования уравнения, когда в обеих его частях стоят логарифмы с одинаковыми основаниями, которые мы можем «зачеркнуть». Отличное знание свойств логарифма, учет области определения, выполнение проверки – залог успеха при решении логарифмических уравнений.

Источник

Основные свойства логарифмов

Логарифмы, как и любые числа, можно складывать, вычитать и всячески преобразовывать. Но поскольку логарифмы — это не совсем обычные числа, здесь есть свои правила, которые называются основными свойствами.

Эти правила обязательно надо знать — без них не решается ни одна серьезная логарифмическая задача. К тому же, их совсем немного — все можно выучить за один день. Итак, приступим.

Сложение и вычитание логарифмов

Итак, сумма логарифмов равна логарифму произведения, а разность — логарифму частного. Обратите внимание: ключевой момент здесь — одинаковые основания. Если основания разные, эти правила не работают!

Эти формулы помогут вычислить логарифмическое выражение даже тогда, когда отдельные его части не считаются (см. урок «Что такое логарифм»). Взгляните на примеры — и убедитесь:

Поскольку основания у логарифмов одинаковые, используем формулу суммы:
log₆ 4 + log₆ 9 = log₆ (4 · 9) = log₆ 36 = 2.

Основания одинаковые, используем формулу разности:
log₂ 48 − log₂ 3 = log₂ (48 : 3) = log₂ 16 = 4.

Задача. Найдите значение выражения: log₃ 135 − log₃ 5.

Снова основания одинаковые, поэтому имеем:
log₃ 135 − log₃ 5 = log₃ (135 : 5) = log₃ 27 = 3.

Как видите, исходные выражения составлены из «плохих» логарифмов, которые отдельно не считаются. Но после преобразований получаются вполне нормальные числа. На этом факте построены многие контрольные работы. Да что контрольные — подобные выражения на полном серьезе (иногда — практически без изменений) предлагаются на ЕГЭ.

Вынесение показателя степени из логарифма

Теперь немного усложним задачу. Что, если в основании или аргументе логарифма стоит степень? Тогда показатель этой степени можно вынести за знак логарифма по следующим правилам:

Несложно заметить, что последнее правило следует их первых двух. Но лучше его все-таки помнить — в некоторых случаях это значительно сократит объем вычислений.

Разумеется, все эти правила имеют смысл при соблюдении ОДЗ логарифма: a > 0, a ≠ 1, x > 0. И еще: учитесь применять все формулы не только слева направо, но и наоборот, т.е. можно вносить числа, стоящие перед знаком логарифма, в сам логарифм. Именно это чаще всего и требуется.

Избавимся от степени в аргументе по первой формуле:
log₇ 49 6 = 6 · log₇ 49 = 6 · 2 = 12

Задача. Найдите значение выражения:

[Подпись к рисунку]

[Подпись к рисунку]

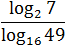
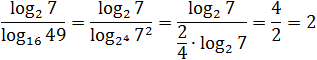
Думаю, к последнему примеру требуются пояснения. Куда исчезли логарифмы? До самого последнего момента мы работаем только со знаменателем. Представили основание и аргумент стоящего там логарифма в виде степеней и вынесли показатели — получили «трехэтажную» дробь.

Теперь посмотрим на основную дробь. В числителе и знаменателе стоит одно и то же число: log₂ 7. Поскольку log₂ 7 ≠ 0, можем сократить дробь — в знаменателе останется 2/4. По правилам арифметики, четверку можно перенести в числитель, что и было сделано. В результате получился ответ: 2.

Переход к новому основанию

Говоря о правилах сложения и вычитания логарифмов, я специально подчеркивал, что они работают только при одинаковых основаниях. А что, если основания разные? Что, если они не являются точными степенями одного и того же числа?

На помощь приходят формулы перехода к новому основанию. Сформулируем их в виде теоремы:

[Подпись к рисунку]

[Подпись к рисунку]

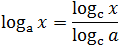
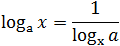
Из второй формулы следует, что можно менять местами основание и аргумент логарифма, но при этом все выражение «переворачивается», т.е. логарифм оказывается в знаменателе.

Эти формулы редко встречается в обычных числовых выражениях. Оценить, насколько они удобны, можно только при решении логарифмических уравнений и неравенств.

Впрочем, существуют задачи, которые вообще не решаются иначе как переходом к новому основанию. Рассмотрим парочку таких:

Задача. Найдите значение выражения: log₅ 16 · log₂ 25.

Заметим, что в аргументах обоих логарифмов стоят точные степени. Вынесем показатели: log₅ 16 = log₅ 2 4 = 4log₅ 2; log₂ 25 = log₂ 5 2 = 2log₂ 5;

А теперь «перевернем» второй логарифм:

[Подпись к рисунку]

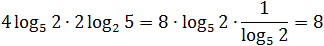
Поскольку от перестановки множителей произведение не меняется, мы спокойно перемножили четверку и двойку, а затем разобрались с логарифмами.

Задача. Найдите значение выражения: log₉ 100 · lg 3.

Основание и аргумент первого логарифма — точные степени. Запишем это и избавимся от показателей:

[Подпись к рисунку]

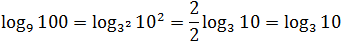
Теперь избавимся от десятичного логарифма, перейдя к новому основанию:

[Подпись к рисунку]

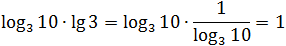
Основное логарифмическое тождество

Часто в процессе решения требуется представить число как логарифм по заданному основанию. В этом случае нам помогут формулы:

В первом случае число n становится показателем степени, стоящей в аргументе. Число n может быть абсолютно любым, ведь это просто значение логарифма.

Подобно формулам перехода к новому основанию, основное логарифмическое тождество иногда бывает единственно возможным решением.

Задача. Найдите значение выражения:

[Подпись к рисунку]

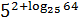
Заметим, что log₂₅ 64 = log₅ 8 — просто вынесли квадрат из основания и аргумента логарифма. Учитывая правила умножения степеней с одинаковым основанием, получаем:

[Подпись к рисунку]

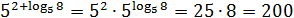
Если кто-то не в курсе, это была настоящая задача из ЕГЭ 🙂

Логарифмическая единица и логарифмический ноль

В заключение приведу два тождества, которые сложно назвать свойствами — скорее, это следствия из определения логарифма. Они постоянно встречаются в задачах и, что удивительно, создают проблемы даже для «продвинутых» учеников.

Вот и все свойства. Обязательно потренируйтесь применять их на практике! Скачайте шпаргалку в начале урока, распечатайте ее — и решайте задачи.

Источник