что делать если степень дробная

Возведение в степень: правила, примеры

Мы разобрались, что вообще из себя представляет степень числа. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. возводить числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя. Все определения будут проиллюстрированы примерами.

Понятие возведения в степень

Начнем с формулирования базовых определений.

Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.

Как возвести число в натуральную степень

Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.

Решение

Возьмем пример посложнее.

Вычислите значение 3 2 7 2

Решение

Выполним эти действия и получим ответ: 3 2 7 · 3 2 7 = 23 7 · 23 7 = 529 49 = 10 39 49

Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.

Решение

Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:

Это понятно из записи .

От основания степени это не зависит.

Как возвести число в целую степень

В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими степенями, мы уже рассказали выше.

Решение

Решение

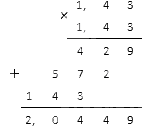
Вычисляем квадрат в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом:

Как возвести число в дробную степень

Проиллюстрируем на примере.

Решение

Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.

Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и считать, как указано выше.

Решение

Как возвести число в иррациональную степень

Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.

Вычислите приближенное значение 2 в степени 1,174367.

Решение

Источник

Дробная степень числа

Дробный показатель

Число с дробным показателем степени равно корню с показателем, равным знаменателю, и подкоренным числом в степени, равной числителю.

Чтобы разобраться, почему число в дробной степени равно корню, надо вспомнить правило извлечения корня из степени:

Чтобы извлечь корень из степени, надо показатель степени разделить на показатель корня:

Следовательно, если показатель степени не делится на показатель корня, то получается дробная степень:

Поэтому извлечение корня всегда может быть заменено возведением в степень.

Действия над степенями с дробными показателями

Действия над степенями с дробными показателями совершаются по тем же правилам, которые установлены для степеней с целым показателем.

При доказательстве этого положения, будем сначала предполагать, что члены дробей: и , служащих показателями степеней, положительны.

В частном случае n или q могут равняться единице.

При умножении дробных степеней с одинаковыми основаниями их показатели складываются:

При делении дробных степеней с одинаковыми основаниями из показателя делимого вычитается показатель делителя:

Чтобы возвести степень в другую степень, в случае дробных показателей, достаточно перемножить показатели степеней:

Чтобы извлечь корень из дробной степени, достаточно показатель степени разделить на показатель корня:

Правила действий применимы не только к положительным дробным показателям, но и к отрицательным.

Источник

Дробная степень

Какими свойствами обладает степень с дробным показателем (дробная степень)? Как выполнить возведение числа в дробную степень?

1) Степенью числа a (a>0) с рациональным показателем r

где m — целое число, n — натуральное число (n>1), называется число

При a

Выполнить возведение в дробную степень:

Если показатель степени — десятичная дробь, нужно предварительно перевести ее в обыкновенную.

Смешанное число нужно предварительно перевести в неправильную дробь:

А как вычисляется отрицательная дробная степень?

Степень с отрицательным рациональным показателем также определена только для a>0:

При возведении обыкновенной дроби в степень с отрицательным показателем удобно использовать формулу:

Выполнить возведение в степень с отрицательным рациональным показателем:

Источник

Алгебра

А Вы уже инвестируете?
Слышали про акцию в подарок?

Зарегистрируйся по этой ссылке
и получи акцию до 100.000 руб

План урока:

Степень с рациональным показателем

Напомним, что в 7 классе мы впервые познакомились с понятием степени, причем тогда рассматривались случаи, когда показателем степени является натуральное число. В 8 классе понятие степени было расширено, теперь в него включались случаи, когда показатель являлся целым числом. Настоятельно рекомендуем перечитать соответствующие уроки. Сегодня же мы можем сделать ещё один шаг вперед и рассмотреть степени с рациональными показателями.

При расширении понятия степени важно обеспечить то, чтобы уже известные правила работы с целыми степенями работали и для дробных показателей. Одно из свойств степеней выглядит так:

Подставим в эту формулу следующие значения переменных:

Мы специально выбрали эти числа такими, чтобы произведение mn равнялось единице:

Подставляем эти значения:

(3 1/6 ) 6 = 3 1/6 • 6 = 3 1 = 3

Однако по определению корня n-ой степени число, дающее при возведении в шестую степень тройку, является корнем шестой степени из трех. То есть можно записать:

С помощью подобных преобразований нам удалось указать, чему равно число, возведенное в дробную степень. Аналогично можно показать, что для любого а > 0 справедлива формула:

Действительно, если возвести левую часть в n-ую степень, то получим:

(а 1/ n ) n = a 1/ n • n = a

Значит, по определению корня n-ой степени

Ограничение а > 0 необходимо для того, чтобы не рассматривать случаи, когда подкоренное выражение является отрицательным.

C учетом этого выполним преобразование:

В результате несложных преобразований нам удалось получить формулу, позволяющую возводить число в степень, у которой рациональный показатель!

Приведем несколько примеров вычисления дробных степеней:

Часто при вычислениях удобнее сначала извлечь корень из числа, а потом полученный результат возвести в степень:

Напомним, что одну и ту же дробь можно представить разными способами, например:

1/2 = 2/4 = 3/6 = 4/8 = 5/10 = 0,5

Возникает вопрос – изменится ли значение дробной степени, если мы приведем дробь к новому знаменателю? Очевидно, что нет, но всё же убедимся в этом на примере. Сначала возведем в степень 1/2 число 25:

Теперь заменим дробь 1/2 на идентичную ей дробь 2/4:

Согласитесь, возводить число 81 в 25-ую степень не очень легко! Поэтому поступим иначе. Сократим дробь 25/100:

0,25 = 25/100 = 25/(25•4) = 1/4

Теперь вычисления будет более простыми:

Вообще легко запомнить, что 0,25 = 1/4, а 0,5 = 1/2. Замена десятичных дробей обыкновенными дробями сильно упрощает вычисления. Приведем примеры:

Свойства дробных степеней и операции с ними

Когда мы изучали степени с целыми показателями, мы выяснили, что правила работы с ними ничем не отличаются от правил работы со степенями с натуральным показателем. Оказывается, эти же правила работают и для степеней с рациональным показателем. Сформулируем основные свойства дробных степеней.

Например, справедливы следующие действия:

5 0,5 •5 2,5 = 5 0,5 + 2,5 = 5 3 = 125

19 5/3 •19 1/3 = 19 5/3 + 1/3 = 19 2 = 361

29,36 –0,37 •29,36 1,37 = 29,36 –0,37 + 1,37 = 29,36 1 = 29,36

Вот несколько примеров подобных вычислений:

17 4,5 :17 3,5 = 17 4,5–3,5 = 17 1 = 1

4 9,36 :4 6,36 = 4 9,36–6,36 = 4 3 = 64

20 12 :20 14 = 20 12–14 = 20 –2

Проиллюстрируем это правило примерами:

(6 0,25 ) 8 = 6 0,25•8 = 6 2 = 36

(9 3/2 ) 2 = 9 (3/2)•2 = 9 3 = 729

(25 4 ) 0,125 = 25 4•0,125 = 25 0,5 = 5

Покажем, как можно применять данное правило:

4 1/6 •16 1/6 = (4•64) 1/6 = 64 1/6 = 2

0,5 1,5 •50 1,5 = (0,5•50) 1,5 = 25 1,5 = 25 1+0,5 = 25 1 •25 0,5 = 25•5 = 125

4,9 0,5 •10 0,5 = (4,9•10) 0,5 = 49 0,5 =7

Это правило можно применять следующим образом:

360 0,5 :10 0,5 = (360:10) 0,5 = 36 0,5 = 6

500 3 :50 3 = (500:50) 3 = 10 3 = 1000

6,25 1/4 :0,01 1/4 = (6,25:0,01) 1/4 = 625 1/4 = 5

Заметим, что степени очень удобны тем, что с их помощью легко упростить работу с корнями, ведь если

то верное и обратное:

То есть любое выражение с корнями в виде степени с рациональным показателем.

Пример. Вычислите значение выражения

Решение. Корней много, поэтому для удобства заменим их степенями

Получили тоже самое выражение, но в более компактном виде. Посчитаем его значение:

(9 1/4 ) 1/5 •3 9/10 = (9 0,25 ) 0,2 •3 0,9 = 9 0,25•0,2 •3 0,9 = 9 0,05 •3 0,9 = (3 2 ) 0,05 •3 0,9 =

=3 2•0,05 •3 0,9 = 3 0,1 •3 0,9 = 3 0,1•0,9 = 3 1 = 3

Пример. Упростите выражение

(81 n+1 – 65•81 n ) 0,25

Решение. Степень 81 n+1 можно представить как произведение:

81 n+1 = 81 n •81 1 = 81•81 n

С учетом этого можно записать:

(81 n+1 – 65•81 n ) 0,25 = (81•81 n – 65•81 n ) 0,25 = (81 n (81 – 65)) 0,25 =

= (81 n •16) 0,25 = 81 0,25 n •16 0,25 = 81 0,25 n •16 1/4 = 2•81 0,25 n

Сравнение степеней

Напомним, что из двух корней n-ой степени больше тот, у которого больше подкоренное выражение:

Отсюда следует вывод, что если a 1/ n 1/ n

теперь возведем каждую часть этого неравенства в степень m. Тогда получим неравенство:

Получили, что из двух степеней с одинаковыми показателями меньше та, у которой меньше основание (правила сравнения будем нумеровать, чтобы на них удобнее было ссылаться):

В частности, справедливы следующие неравенства:

Здесь мы рассматривали случаи, когда показатель степени является положительным числом. А что делать, если он отрицательный? Тогда степень следует «перевернуть», воспользовавшись уже известной вам формулой:

Пример. Сравните выражения с рациональным показателем степени:

20 –3,14 и 50 –3,14

Решение. Избавимся от знака минус в показателе:

20 –3,14 = (1/20) 3,14 = 0,05 3,14

50 –3,14 = (1/50) 3,14 = 0,02 3,14

Получили две степени с одинаковым и, что принципиально важно, положительным показателем. Из них больше та, у которой больше основание. То есть из неравенства 0,02 3,14 3,14

Особенным является случай, когда показатель степени равен нулю. Напомним, что любое число в нулевой степени (кроме самого нуля) равно единице, а выражение 0 0 не имеет смысл. Это значит, что числа в нулевой степени равны друг другу, даже если у них разные основания:

18,3546 0 = 12,3647 0 = 1

Несколько сложнее сравнивать числа, у которых одинаковые основания, но различные показатели. Здесь возможны три случая – основание либо равно единице, либо больше неё, либо меньше неё.

На основании этого правила можно записать, что:

Единица в любой степени равна самой себе. Поэтому, если у двух чисел в основании записана именно она, то они должны быть равны друг другу:

1 –7,56 = 1 –0,15 = 1 0,236 = 1 521,36 = 1

0,5 = 1/2 = 1/(2 1 ) = 2 –1

0,5 7,6 = (2 –1 ) 7,6 = 2 –7,6

0,5 8,9 = (2 –1 ) 8,9 = 2 –8,9

Такие числа мы уже умеем сравнивать. Так как

Например, справедливы неравенства:

0,57 15,36 > 0,57 16,47

Рассмотрим чуть более сложное задание на сравнение степеней, где надо использовать одновременно несколько правил.

Пример. Докажите, что

0,9 0,9 + 0,8 0,8 + 0,7 0,7 1/3

Решение. Напрямую вычислить значение выражений в правой и левой части затруднительно. Однако мы можем усиливать неравенство, чтобы получить более простые выражения.

Усилить неравенство – это значит увеличить его меньшую или уменьшить большую часть. Например, неравенство 10 1/3 :

Также ясно, что 27 1/3 1/3 (правило 1). Усилим исходное неравенство:

0,9 0,9 + 0,8 0,8 + 0,7 0,7 1/3 (1)

Действительно, если (1) справедливо, то мы можем записать двойное неравенство

0,9 0,9 + 0,8 0,8 + 0,7 0,7 1/3 1/3

Опустив здесь среднюю часть, получим исходное неравенство. Так как 27 1/3 = 3, мы можем переписать (1) так:

0,9 0,9 + 0,8 0,8 + 0,7 0,7 0,8 0,8 (снова используем правило 1). С другой стороны, 0,9 0,8 0,7 (правило 3). Значит, можно записать двойное неравенство:

Их левые части стоят в (2). Следовательно, можно усилить (2):

0,9 0,7 + 0,9 0,7 + 0,9 0,7 0,7 0,7 0,7 :

Из правила 1 следует, что (4) справедливо. Но мы получили его, усиливая исходное неравенство. Из справедливости более сильного неравенства следует и справедливость более слабого. Следовательно, из справедливости (4) вытекает верность исходного неравенства, которое и надо было доказать.

Источник

Возведение в дробную степень

Вы будете перенаправлены на Автор24

Использование дробей в качестве степеней значительно упрощает жизнь по сравнению с записью выражений с помощью корней. Это связано с тем, что совершать арифметические действия с дробями легче, чем применять и помнить свойства корней. Поэтому ниже мы рассмотрим, как перейти от корней к числу в дробной степени.

Возведение в дробную степень проводится соответственно следующему правилу:

В математической форме это тождество записывается так:

Следует отметить, что в случае использования в качестве записи дробной степени вместо корней есть одно важное правило. Запрещается возводить в дробную степень отрицательные числа.

Это связано с тем, что в таком случае можно прийти к невыполнимому равенству, например:

Правило для возведения степени в степень в случае, когда показатель степени является дробным числом, выполняется также как и для обычной целой степени, то есть:

В математической форме это выглядит так:

Правило для возведения числа в дробную степень справедливо не только для обыкновенных дробей, но и для десятичных и неправильных.

В случае, если необходимо возвести число в десятичную или неправильную дробь, сначала необходимо перевести её в обычную чтобы стали видны показатели степени числа и корня.

Возведение в нецелую отрицательную степень проводится по тем же правилам, что и возведение в целую отрицательную степень, то есть:

Запишем в математической форме:

Вычислите арифметические корни из следующих выражений:

Источник