что делать если синус отрицательный
sin(-a),cos(-a),tg(-a),ctg(-a). Минус в аргументе синуса, косинуса
И сразу два важных замечания.
Многие ученики думают, что если можно вынести минус из тригонометрической функции, то можно вынести и число, но это не так:
Квадрат меняет ситуацию. Всё дело в том, что \(sin^2(-x)=(sin(-x) )^2=(-sin\,x )^2=sin^2x\), т.е. минус все равно выносится, но так как синуса два и они перемножаются, то в итоге получается плюс.
Примеры из ЕГЭ
Из рисунка видно, что и косинус, и синус положителен. Косинус из трех стандартных значений \(\frac<1><2>\), \(\frac<\sqrt<2>><2>\), \(\frac<\sqrt<3>><2>\) принимает наименьшее т.е. \(cos\,\frac<π><3>=\frac<1><2>\). Синус из трех стандартных значений будет равен среднему т.е. \(sin\,\frac<π><4>=\frac<\sqrt<2>><2>\). Получается:
Если вы не поняли почему \(\frac<π><3>\) и \(\frac<π><4>\) находятся на круге там, где мы из обозначили, то читайте статью « Как обозначать числа с пи на числовой окружности? ». А если не поняли, как мы нашли синус и косинус, то читайте статью « Как найти синус и косинус без тригонометрической таблицы ».
Пример (ЕГЭ). Найдите значение выражения \(44\sqrt<3>\,tg\,(-480^° )\).
Решение. \(44\sqrt<3>\,tg(-480^° )=-44\sqrt<3>\,tg(480^° )=-44\sqrt<3>\,tg(360^°+120^° )=-44\sqrt<3>\,tg(360^°+90^°+30^°)\).
Находим \(480^°\) на окружности:
Соединяем точку, соответствующую \(480^°\) и центр окружности, и продляем до оси тангенсов:
Мы попадаем в самое маленькое (из стандартных) значение тангенса.
Значит, \(tg(480^° )=-\sqrt<3>\).
В итоге имеем: \(44\sqrt <3>tg(-480^° )=-44\sqrt<3>\cdot(-\sqrt<3>)=44\cdot 3=132\).
Ответ: \(132\).
Если вам не понятно, как мы нашли значение тангенса, то читайте статью « Как найти тангенс и котангенс без тригонометрической таблицы? ».
Доказательства формул с минусом в аргументе:
Геометрия. Урок 1. Тригонометрия
Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Тригонометрия в прямоугольном треугольнике
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.
Синус угла – отношение противолежащего катета к гипотенузе.
sin α = Противолежащий катет гипотенуза
Косинус угла – отношение прилежащего катета к гипотенузе.
cos α = Прилежащий катет гипотенуза
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
tg α = Противолежащий катет Прилежащий катет
Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).
ctg α = Прилежащий катет Противолежащий катет
tg ∠ A = sin ∠ A cos ∠ A = C B A C
ctg ∠ A = cos ∠ A sin ∠ A = A C C B
tg ∠ B = sin ∠ B cos ∠ B = A C C B
ctg ∠ B = cos ∠ B sin ∠ B = C B A C
Тригонометрия: Тригонометрический круг
Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Рассмотрим прямоугольный треугольник A O B :
cos α = O B O A = O B 1 = O B
sin α = A B O A = A B 1 = A B
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Основное тригонометрическое тождество
sin 2 α + cos 2 α = 1
Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :
A B 2 + O B 2 = O A 2
sin 2 α + cos 2 α = R 2
sin 2 α + cos 2 α = 1
Тригонометрия: Таблица значений тригонометрических функций
Тригонометрия: градусы и радианы
Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!
Тригонометрия: Формулы приведения
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,
можно заметить, что:
sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °
sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °
sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °
sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °
cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °
cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °
cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °
cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °
Рассмотрим тупой угол β :
Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:
sin ( 180 ° − α ) = sin α
cos ( 180 ° − α ) = − cos α
tg ( 180 ° − α ) = − tg α
ctg ( 180 ° − α ) = − ctg α
Тригонометрия: Теорема синусов
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.
a sin ∠ A = b sin ∠ B = c sin ∠ C
Тригонометрия: Расширенная теорема синусов
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R
Тригонометрия: Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A
b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B
c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с тригонометрией.
Тригонометрия: Тригонометрические уравнения
Это тема 10-11 классов.
Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!
Основное тригонометрическое тождество
9 класс, 10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Связь между sin и cos одного угла
Вы уже наверняка знаете, что тождественный — это равный.
Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция.
Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:
sin 2 α + cos 2 α = 1
Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.
Равенство tg 2 α + 1 = 1/cos 2 α и равенство 1 + сtg 2 α + 1 = 1/sin 2 α выводят из основного тождества, разделив обе части на sin 2 α и cos 2 α.
В результате деления получаем:
Поэтому основному тригонометрическому тождеству уделяется максимум внимания. Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая.
sin 2 α + cos 2 α = 1
Сумма квадратов синуса и косинуса одного угла тождественно равна единице.
Чтобы доказать тождество, обратимся к теме единичной окружности.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.
Докажем тождество sin 2 α + cos 2 α = 1
Образовался прямоугольный треугольник OA1B.
Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:
Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.
Как правило, в задачках с подобными формулами уже есть условия, которые помогают определиться со знаком. Обычно такое условие — указание на координатную четверть. Таким образом без труда можно определить, какой знак нам требуется.
Тангенс и котангенс через синус и косинус
Из всего этого множества красивых, но не сильно понятных слов, можно сделать вывод о зависимости одного от другого. Такая связь помогает отдельно преобразовывать нужные величины.
Исходя из определений:
Это позволяет сделать вывод, что тригонометрические тождества

задаются sin и cos углов.
Отсюда следует, что тангенс угла — это отношение синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.
Отдельно стоит обратить внимание на то, что тригонометрические тождества

верны для всех углов α, значения которых вписываются в диапазон.
применимо для любого угла α, не равного π * z, где z — это любое целое число.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Связь между тангенсом и котангенсом
Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.
Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число. В противном случае, функции не будут определены.
Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.
tg α * ctg α = 1.
Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.
Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу a обратно число b, а числу b обратно число a. Короче, и так, и эдак.
Тангенс и косинус, котангенс и синус
Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла — с синусом.
Эта связь становится очевидна, если взглянуть на тождества:
Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.
Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.
Вывести оба этих тождества можно из основного тригонометрического тождества:
sin 2 α + cos 2 α = 1.
Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами.
Основные тригонометрические тождества
sin 2 α + cos 2 α = 1
tg 2 α + 1 =
1 + ctg 2 α =
Чтобы тратить еще меньше времени на решение задач, сохраняйте таблицу значений тригонометрических функции углов, которые чаще всего встречаются в задачах.
Примеры решения задач
Разберем пару задачек, для решения которых нужно знать основные тождества. Рассмотрите внимательно предложенные решения и потренируйтесь самостоятельно.
Задачка 1. Найдите cos α, tg α, ctg α при условии, что sin α = 12/13.
Задачка 2. Найдите значение cos α,
если:
Подставляем значения sin α:
Как видите, задачи решаются достаточно просто, нужно лишь верно применять формулы основных тождеств.
Гайморит: симптомы, особенности лечения и правила профилактики
Гайморит – это воспалительный процесс в области гайморовой пазухи, расположенной в толще черепной кости над верхней челюстью, слева и справа. Этот процесс является одной из разновидностей синуситов (это общее название для воспалительных процессов в области придаточных пазух – лобной, гайморовой, решетчатой или клиновидной). Обычно воспалительный процесс затрагивает слизистые оболочки, выстилающие пазухи изнутри, реже затрагиваются более глубокие слои тканей, вплоть до костных структур. Обычно процесс возникает как осложнение вирусных или бактериальных инфекций в области носоглотки и верхних дыхательных путей.
Исходя из причины развития, механизмов формирования и симптомов, гайморит бывает нескольких типов. Выделение каждого из них важно для определения тактики лечения, прогноза и разработки мер профилактики.
Острый – развивается быстро, как осложнение ОРВИ, насморков, простудных заболеваний, воспаления в области корней зубов на верхней челюсти. Возбудители проникают через каналы, соединяющие пазухи с полостью носа с гайморовыми пазухами, размножаются в полости. Тело начинает активно вырабатывать иммунные клетки и слизь, чтобы обезвредить патогенные организмы. Если слизь закупорит проток пазухи, возникает давление на стенки, усиление воспалительного процесса. По мере очищения пазухи от содержимого воспалительный процесс постепенно затухает.
Хронический – воспалительный процесс, который длится более 4 недель, имеет вялое или волнообразное течение, с периодами обострений. Обычно возникает из-за не долеченной острой формы, наличия аденоидов, тонзиллитов, отитов.
Гнойный – обычно становится осложнением острой формы либо обострения хронического процесса, если процесс не лечится, предпринимаются попытки самолечения или пациент переносит инфекцию на ногах. Патогенные бактерии накапливаются в пазухах, в смеси с лейкоцитами образуют гнойное содержимое. Самое опасное осложнение при этой форме – прорыв гноя в полость черепа, поражение костных тканей, мозга.
Двусторонний – одна из тяжелых форм, поражение локализовано сразу в обеих пазухах – левой и правой. Нередко возникает как осложнение инфекций в полости рта и носоглотки, обычно грибковой или бактериальной. Обычно имеет острое течение, редко переходит в хроническую форму.
Аллергическое поражение возникает у пациентов, страдающих от чрезмерно активной реакции иммунной системы на различные вещества. Особенно часто эта форма синусита бывает при поллинозе, круглогодичном рините, реакции на плесень, пылевых клещей.
Катаральный – преимущественно бывает у детей. Он развивается при проникновении в полость пазух патогенных организмов, что формирует отек и раздражение слизистых. Считается самой легкой формой болезни, проходящей при активном лечении без осложнений и последствий.
Полипозная форма формируется при образовании полипозных разрастаний слизистых из-за чрезмерно быстрого деления клеток. Рост полипов могут провоцировать инфекции, травмы, велика роль наследственности.
Одонтогенный – формируется как результат серьезных проблем зубов, особенно 4-6 зуба на верхней челюсти, корни которых расположены в непосредственной близости от пазухи. Если возникают проблемы в области корней этих зубов, воспаление и нагноение может переходить на пазуху, она заполняется секретом и воспаляется.
Причины
Придаточные пазухи, включая гайморовы, созданы как естественный барьер на пути инфекций, фильтр для различных опасных веществ в воздухе. Они помогают согревать воздух, увлажнять его и очищать от примесей перед попаданием в гортань, и ниже по респираторному тракту. Основная причина воспаления и появления признаков гайморита – это проникновение бактерий, грибков или вирусов, аллергенов. Реже инфекция попадает с током крови из других, отдаленных очагов.
Нарушать работу пазух могут патологии иммунной системы, частые ОРВИ, респираторная форма аллергии, носительство патогенных бактерий в носоглотке (стафило-, стрепто- или менингококк).
Среди ключевых причин, которые могут привести к развитию гайморита, можно выделить:
Осложнения
Не все люди знают, как начинается гайморит, поэтому многие принимают симптомы за тяжелую простуду и лечатся самостоятельно. Это может привести к определенным осложнениям, отдаленным последствиям. Среди ключевых осложнений можно выделить поражения бронхов и распространение инфекции на легкие, развитие отитов (поражение среднего уха), переход болезни в хроническую форму.
Тяжелый и запущенный, своевременно не вылеченный гайморит может привести к воспалению внутренних органов – сердца, глаз, почек, поражению суставов и мозга, его оболочек. Если образуются гнойные полости в гайморовых пазухах, возможен прорыв гноя в кровь (возникает сепсис), проникновение его в соседние пазухи с развитием пансинусита, воспаление мозговых оболочек с явлениями менингита. Всех этих осложнений можно избежать при полноценном лечении гайморита под руководством лор-врача.
Симптомы и диагностика
Конечно, при развитии гайморита нужно немедленно обращаться к врачу, но как понять, что гайморит начался? Начальные признаки неспецифичные – это повышение температуры от незначительной до высокой, сильная слабость, заложенность носа или обильные густые выделения, болезненность в проекции пазух или в области лица.
Боль при гайморите может быть различной – от тупой, давящей до сильной, мучительной. Она локализуется в подглазничной области, может отдавать в область переносицы, лобную зону или верхние зубы. При надавливании на область пазух или наклонах головы вперед она усиливается, распространяясь по подглазничной области. Могут краснеть и отекать веки.
Врачи отмечают некоторые особенности того, как проявляется болезнь в определенных возрастных группах. Так, у взрослых самым ключевым признаком могут быть болевые ощущения, головная боль, нарушение восприятия запахов. Может меняться голос, он становится гнусавым, нос сильно заложен, выделяется полупрозрачная или желто-зеленая слизь. Высокая лихорадка типична для острой формы, при хроническом или аллергическом гайморите болезнь может протекать без температуры.
На фоне поражения пазух возможно слезотечение, неприятный привкус во рту, слабость, постоянное утомление, нарушения аппетита, расстройства сна, ознобы и приступы кашля.
Заразен ли гайморит? Само по себе воспаление – это результат влияния патогенных факторов, и это не заразно. Бактерии или вирусы, которые спровоцировали заболевание, могут передаваться от человека к человеку, но не обязательно вызовут поражение пазух.
Диагноз гайморита ставит лор-врач после проведения ряда тестов и осмотра пациента. Важно подробно рассказать, как началось заболевание, какие жалобы были ранее и имеются в данный момент. Врач осмотрит полость носа и глотку, прощупает проекцию пазух, определяя болезненность.
Дополнительно могут понадобиться КТ или МРТ придаточных пазух, рентгенограмма, УЗИ исследование, эндоскопия носоглотки, при необходимости – биопсия полипозных образований. Назначаются анализы крови, посевы отделяемой из носа слизи для определения флоры, чтобы подобрать необходимые препараты.
Как лечить у взрослого
Терапия болезни должна быть комплексной. Она направлена на борьбу с инфекцией, устранение воспаления, налаживание оттока слизи из пазух и улучшение носового дыхания. В неосложненных случаях возможно лечение гайморита дома под постоянным контролем оториноларинголога. В тяжелых случаях и при необходимости хирургического лечения пациент госпитализируется в стационар.
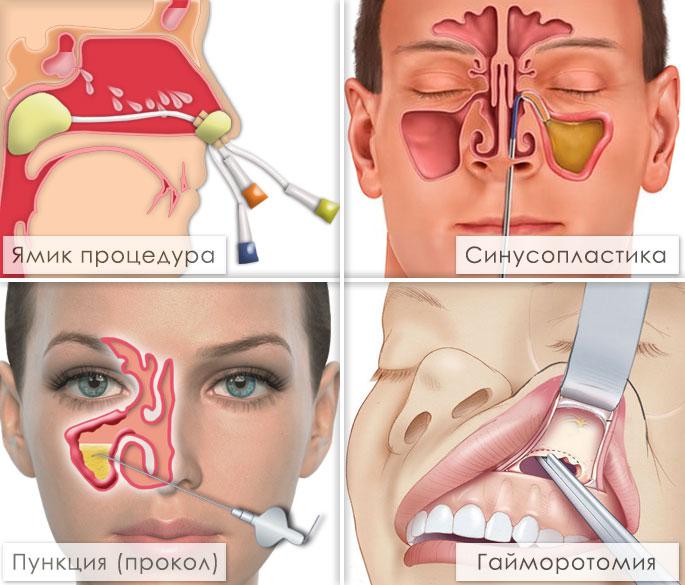
Возможно консервативное лечение с назначением антибактериальных препаратов, противовоспалительных средств, антигистаминных препаратов и различных капель, спреев для носа. Также применяют пункционное лечение или хирургические вмешательства. Выбор зависит от возраста пациента, вида патологии, тяжести состояния и возможных осложнений.
Многим пациентам назначают пункции (с местным обезболиванием) – они помогают удалить гнойное содержимое, помочь в оценке характера воспаления, плюс приносят существенное облегчение. После удаления содержимого пазухи промывают физраствором или фурациллином, вводят растворы антибиотиков и противовоспалительные препараты. Минус подобной тактики – не всегда достаточно одного прокола, поэтому требуется курс процедур в течение нескольких недель. Метод достаточно неприятный, имеет ряд противопоказаний и осложнений, процедура болезненна как во время прокола, так и после него.