что делать если распределение ненормальное
Как выполнить регрессию для ненормальных данных, которые остаются ненормальными при преобразовании?
У меня есть некоторые данные (158 случаев), которые были получены из ответа по шкале Лайкерта на 21 вопросник. Я действительно хочу / нужно провести регрессионный анализ, чтобы увидеть, какие пункты в анкете предсказывают реакцию на общий элемент (удовлетворенность). Ответы обычно не распределяются (в соответствии с тестами KS), и я преобразовал их всеми возможными способами (обратный, log, log10, sqrt, квадрат), и он упрямо отказывается от нормального распределения. Остаточный график выглядит повсеместно, поэтому я считаю, что на самом деле нельзя делать линейную регрессию и делать вид, что она ведет себя нормально (это также не распределение Пуассона). Я думаю, что это потому, что ответы очень тесно сгруппированы (среднее значение составляет 3,91, 95% ДИ от 3,88 до 3,95).
Итак, я думаю, что мне либо нужен новый способ преобразования моих данных, либо нужна какая-то непараметрическая регрессия, но я не знаю ничего, что я мог бы сделать в SPSS.
Вместо того, чтобы полагаться на тест на нормальность остатков, попробуйте оценить нормальность с рациональной оценкой. Тесты нормальности не говорят вам, что ваши данные нормальные, только то, что это не так. Но, учитывая, что данные являются образцом, вы можете быть совершенно уверены, что они не являются нормальными без теста. Требование примерно нормальное. Тест не может вам этого сказать. Тесты также становятся очень чувствительными при больших N или, более серьезно, различаются по чувствительности с N. Ваш N находится в том диапазоне, где чувствительность начинает повышаться. Если вы запустите следующую симуляцию в R несколько раз и посмотрите на графики, то увидите, что тест нормальности говорит «ненормально» для большого числа нормальных распределений.
Стандартный остаточный график в SPSS не очень полезен для оценки нормальности. Вы можете увидеть выбросы, диапазон, качество подгонки и, возможно, даже рычаг. Но нормальность трудно вывести из этого. Попробуйте следующее моделирование, сравнивая гистограммы, квантиль-квантиль нормальных графиков и остаточных графиков.
Невероятно сложно отличить нормальность или многое от последнего графика и, следовательно, не очень хорошо диагностировать нормальность.
Таким образом, как правило, рекомендуется не полагаться на тесты нормальности, а скорее на диагностические графики остатков. Без этих графиков или фактических значений в вашем вопросе кому-то очень сложно дать вам твердый совет относительно того, что нужно вашим данным с точки зрения анализа или преобразования. Чтобы получить лучшую помощь, предоставьте необработанные данные.
Во-первых, регрессия OLS не делает никаких предположений о данных, она делает предположения об ошибках, оцененных по остаточным значениям.
Во-вторых, преобразование данных для приведения в соответствие модели, на мой взгляд, является неправильным подходом. Вы хотите, чтобы ваша модель соответствовала вашей проблеме, а не наоборот. В старые времена регрессия OLS была «единственной игрой в городе» из-за медленных компьютеров, но это уже не так.
В-четвертых, я немного обеспокоен вашим заявлением:
Я действительно хочу / нужно провести регрессионный анализ, чтобы увидеть, какие пункты в анкете предсказывают реакцию на общий элемент (удовлетворенность)
Если элементы были суммированы или каким-либо образом объединены, чтобы составить общий масштаб, то регрессия не является правильным подходом вообще. Вы, вероятно, хотите факторный анализ.
В целом, существует два возможных подхода к вашей проблеме: один, который оправдан с теоретической точки зрения, но потенциально невозможен для реализации на практике, а другой является более эвристическим.
Теоретически оптимальный подход (который вы, к сожалению, вряд ли сможете использовать) заключается в том, чтобы вычислить регрессию, вернувшись к прямому применению так называемого метода максимальной вероятности. Связь между оценкой максимального правдоподобия (которая на самом деле является предшествующей и более фундаментальной математической концепцией) и регрессией обычных наименьших квадратов (OLS) (обычный подход, действительный для конкретного, но чрезвычайно распространенного случая, когда все переменные наблюдения независимо являются случайными и нормально распределенными ) описан во многих учебниках по статистике; Одно из обсуждений, которое мне особенно нравится, это раздел 7.1 «Статистического анализа данных» Глена Коуэна. В тех случаях, когда ваши переменные наблюдения обычно не распределяются,
Что делать, если ваши данные не являются нормальными?
Дата публикации Nov 2, 2018
Введение
ЭтоНеделя хэллоуинаМежду этими хитростями и удовольствиями мы, фанаты данных, смеемся над этим милым мемом в социальных сетях.
Вы думаете, что это шутка? Позвольте мне сказать вам, это не смешное дело. Это страшно, правда духа Хэллоуина!
Если мы не можем предположить, что большинство наших данных (делового, социального, экономического или научного происхождения) по крайней мере приблизительно «нормальны» (т. Е. Они получены гауссовым процессом или суммой нескольких таких процессов), то мы обречены!
Вот очень краткий список вещей, которые не будут действительны,
Всемогущее и вездесущее нормальное распределение
Давайте сделаем этот раздел коротким и приятным.
Нормальное (гауссовское) распределение является наиболее широко известным распределением вероятностей. Вот несколько ссылок на статьи, описывающие его мощь и широкую применимость,
Почему ученые данных любят гауссов?
Три основные причины, по которым распространение по Гауссу так популярно у инженеров по машинному обучению и…
towardsdatascience.com
Из-за его появления в различных областях иЦентральная предельная теорема(CLT), это распределение занимает центральное место в науке о данных и аналитике.
В теории вероятностей нормальное (или гауссово, или гауссово, или лапласово-гауссовское) распределение является очень распространенным непрерывным…
en.wikipedia.org
Так в чем проблема?
Это все неуклюжий, в чем проблема?
Проблема в том, что часто вы можете найти дистрибутив для вашего конкретного набора данных, который может не удовлетворять нормальности, то есть свойствам нормального дистрибутива. Но из-за чрезмерной зависимости от предположения о нормальности,Большинство структур бизнес-аналитики специально разработаны для работы с нормально распределенными наборами данных.,
Это почти укоренилось в нашем подсознании.
Допустим, вас просят обнаружить проверку, имеет ли смысл новый пакет данных из какого-либо процесса (инженерного или бизнес). По ‘придать смыслаВы имеете в виду, если новые данныепринадлежатт.е. если он находится в «ожидаемом диапазоне».
Что это за «ожидание»? Как определить количество?
Автоматически, как если бы это было направлено подсознательным двигателем, мы измеряем среднее значение и стандартное отклонение выборочного набора данных и продолжаем проверять, попадают ли новые данные в определенный диапазон стандартных отклонений.
Если нам нужно работать с доверительной вероятностью 95%, то мы будем рады видеть, что данные находятся в пределах 2 стандартных отклонений. Если нам нужно более строгое ограничение, мы проверяем 3 или 4 стандартных отклонения. Мы рассчитываемхолодный полярный континентальный воздухили мы следуемшесть Сигмруководящие принципы длям.д.(частей на миллион) уровень качества.
Все эти расчеты основаны на неявном предположении, что данные о населении (НЕ выборка) следуют гауссовскому распределению, т.е. фундаментальный процесс, на основе которого были получены все данные (в прошлом и в настоящем), определяется шаблоном левая сторона.
Но что произойдет, если данные будут следовать шаблону с правой стороны?
Существует ли более универсальная граница, когда данные НЕ являются нормальными?
В конце дня нам все еще понадобитсяматематически обоснованная техника для количественной оценки нашей достоверностидаже если данные не нормальные. Это означает, что наши расчеты могут немного измениться, но мы все равно должны сказать что-то вроде этого:
«Вероятность наблюдения новой точки данных на определенном расстоянии от среднего значения такая-то и такая-то…»
Очевидно, что нам нужно искать более универсальную границу, чем заветные границы Гаусса 68–95–99,7 (что соответствует стандартному отклонению 1/2/3 от среднего значения).
К счастью, есть одна такая граница, называемая «граница Чебышева».
Что такое Чебышевский переплет и чем он полезен?
Неравенство Чебышева (также называемое неравенством Бинайме-Чебышева) гарантирует, чтодля широкого класса распределений вероятностей не более определенной доли значений может быть больше определенного расстояния от среднего,
В частности, не более1 /К²значений распределения может быть большеКстандартные отклонения от среднего значения (или эквивалентно, по крайней мере,1-1 / k²значения распределения находятся в пределахКстандартные отклонения от среднего значения).
Это относится к практически неограниченным типам вероятностных распределений и работает в гораздо более смягченном предположении, чем нормальность.
Даже если вы ничего не знаете о секретном процессе ваших данныхесть хороший шанс, что вы можете сказать следующее,
«Я уверен, что 75% всех данных должны находиться в пределах 2 стандартных отклонений от среднего»,
Я уверен, что 89% всех данных должны находиться в пределах 3 стандартных отклонений от среднего значения ».
Вот как это выглядит для произвольно выглядящего дистрибутива,
Как это применить?
Таблица выглядит следующим образом (здесь k обозначает много стандартных отклонений от среднего значения),
Видео демонстрация его применения здесь,
В чем подвох? Почему люди не используют эту «более универсальную» границу?
Очевидно, что выгода, глядя на таблицу или математическое определение.Правило Чебышева намного слабее, чем правило Гаусса, когда речь идет о границах данных.,
Следует1 / k²картина по сравнению сэкспоненциально падающийшаблон для нормального распределения.
Например, чтобы связать что-либо с достоверностью 95%, вам необходимо включить данные до 4,5 стандартных отклонений по сравнению только с 2 стандартными отклонениями (для нормальных значений).
Но он все равно может спасти тот день, когда данные не похожи на нормальное распределение.
есть что-нибудь получше?
Есть еще одна граница под названием «Чернофф Бунд«/Неравенство Хеффдингакоторый дает экспоненциально резкое распределение хвоста (по сравнению с 1 / k²) для сумм независимых случайных величин.
Это также может использоваться вместо гауссовского распределения, когда данные не выглядят нормально, но только тогда, когда мы имеем высокую степень уверенности в том, что основной процесс состоит из подпроцессов, которые полностью независимы друг от друга.
К сожалению, во многих социальных и бизнес-случаях окончательные данные являются результатом чрезвычайно сложного взаимодействия многих подпроцессов, которые могут иметь сильную взаимозависимость.
Резюме
В этой статье мы узнали о конкретном типе статистической границы, которая может быть применена к как можно более широкому распределению данных независимо от предположения о нормальности. Это удобно, когда мы очень мало знаем об истинном источнике данных и не можем предположить, что оно следует гауссовскому распределению. Граница следует степенному закону, а не экспоненциальному характеру (как гауссовский) и поэтому является более слабой Но это важный инструмент в вашем репертуаре для анализа любого произвольного типа распределения данных.
Что делать если распределение ненормальное
Непараметрическая статистика и подгонка распределения
Действительно ли большинство переменных имеют нормальное распределение? В рассмотренном примере использовался тот факт, что в повторных выборках равного объемы средние значения (роста людей) будут иметь t распределение (с определенным средним и дисперсией). Однако, это верно лишь, если рассматриваемая переменная (рост) имеет нормальное распределение, т.е. что распределение людей определенного роста нормально распределено.
Дополнительную информацию о нормальном распределении можно посмотреть в разделе Элементарные понятия статистики.
Объем выборки. Другим фактором, часто ограничивающим применимость критериев, основанных на предположении нормальности, является объем или размер выборки, доступной для анализа. До тех пор пока выборка достаточно большая (например, 100 или больше наблюдений), можно считать, что выборочное распределение нормально, даже если вы не уверены, что распределение переменной в популяции, действительно, является нормальным. Тем не менее, если выборка очень мала, то критерии, основанные на нормальности, следует использовать только при наличии уверенности, что переменная действительно имеет нормальное распределение. Однако нет способа проверить это предположение на малой выборке.
Краткий обзор непараметрических процедур
Различия между независимыми группами. Обычно, когда имеются две выборки (например, мужчины и женщины), которые вы хотите сравнить относительно среднего значения некоторой изучаемой переменной, вы используете t-критерий для независимых выборок (в модуле Основные статистики и таблицы). Непараметрическими альтернативами этому критерию являются: критерий серий Вальда-Вольфовица, U критерий Манна-Уитни и двухвыборочный критерий Колмогорова-Смирнова. Если вы имеете несколько групп, то можете использовать дисперсионный анализ (см. Дисперсионный анализ). Его непараметрическими аналогами являются: ранговый дисперсионный анализ Краскела-Уоллиса и медианный тест.
Различия между зависимыми группами. Если вы хотите сравнить две переменные, относящиеся к одной и той же выборке (например, математические успехи студентов в начале и в конце семестра), то обычно используется t-критерий для зависимых выборок (в модуле Основные статистики и таблицы. Альтернативными непараметрическими тестами являются: критерий знаков и критерий Вилкоксона парных сравнений. Если рассматриваемые переменные по природе своей категориальны или являются категоризованными (т.е. представлены в виде частот попавших в определенные категории), то подходящим будет критерий хи-квадрат Макнемара. Если рассматривается более двух переменных, относящихся к одной и той же выборке, то обычно используется дисперсионный анализ (ANOVA) с повторными измерениями. Альтернативным непараметрическим методом является ранговый дисперсионный анализ Фридмана или Q критерий Кохрена (последний применяется, например, если переменная измерена в номинальной шкале). Q критерий Кохрена используется также для оценки изменений частот (долей).
Зависимости между переменными. Для того, чтобы оценить зависимость (связь) между двумя переменными, обычно вычисляют коэффициент корреляции. Непараметрическими аналогами стандартного коэффициента корреляции Пирсона являются статистики Спирмена R, тау Кендалла и коэффициент Гамма (см. Непараметрические корреляции). Если две рассматриваемые переменные по природе своей категориальны, подходящими непараметрическими критериями для тестирования зависимости будут: Хи-квадрат, Фи коэффициент, точный критерий Фишера. Дополнительно доступен критерий зависимости между несколькими переменными так называемый коэффициент конкордации Кендалла. Этот тест часто используется для оценки согласованности мнений независимых экспертов (судей), в частности, баллов, выставленных одному и тому же субъекту.
Какой метод использовать
Нелегко дать простой совет, касающийся использования непараметрических процедур. Каждая непараметрическая процедура в модуле имеет свои достоинства и свои недостатки. Например, двухвыборочный критерий Колмогорова-Смирнова чувствителен не только к различию в положении двух распределений, например, к различиям средних, но также чувствителен и к форме распределения. Критерий Вилкоксона парных сравнений предполагает, что можно ранжировать различия между сравниваемыми наблюдениями. Если это не так, лучше использовать критерий знаков. В общем, если результат исследования является важным (например, оказывает ли людям помощь определенная очень дорогостоящая и болезненная терапия?), то всегда целесообразно применить различные непараметрические тесты. Возможно, результаты проверки (разными тестами) будут различны. В таком случае следует попытаться понять, почему разные тесты дали разные результаты. С другой стороны, непараметрические тесты имеют меньшую статистическую мощность (менее чувствительны), чем их параметрические конкуренты, и если важно обнаружить даже слабые отклонения (например, является ли данная пищевая добавка опасной для людей), следует особенно внимательно выбирать статистику критерия.
Большие массивы данных и непараметрические методы. Непараметрические методы наиболее приемлемы, когда объем выборок мал. Если данных много (например, n > 100), то не имеет смысла использовать непараметрические статистики. Глава Элементарные понятия статистики предлагает краткое ознакомление с центральной предельной теоремой. Главное здесь состоит в том, что когда выборки становятся очень большими, то выборочные средние подчиняются нормальному закону, даже если исходная переменная не является нормальной или измерена с погрешностью. Таким образом, параметрические методы, являющиеся более чувствительными (имеют большую статистическую мощность), всегда подходят для больших выборок. Большинство критериев значимости многих непараметрических статистик, описанных далее, основываются на асимптотической теории (больших выборок) поэтому соответствующие тесты часто не выполняются, если размер выборки становится слишком малым. Обратитесь к описаниям определенных критериев, чтобы узнать больше об их мощности и эффективности.
В некоторых исследовательских проектах можно сформулировать гипотезы относительно распределения рассматриваемой переменной. Например, переменные, значения которых определяются бесконечным числом независимых факторов, распределены по нормальному закону: можно предположить, что рост индивидуума является результатом воздействия многих независимых факторов, таких как различные генетические предрасположенности, болезни, перенесенные в раннем возрасте и т.д. Как следствие, рост имеет тенденцию к нормальному распределению в населении. С другой стороны, если наблюдаемые значения переменной являются результатом очень редких событий, то переменная будет иметь распределение Пуассона (которое иногда называется распределением редких событий). Например, несчастные случаи на производстве можно рассматривать как результат пересечения ряда неудачных событий (на житейском языке стечением маловероятных обстоятельств), поэтому их частота приближенно описывается распределением Пуассона. Эти и другие полезные распределения подробно описываются в соответствующих разделах.
Гипотеза нормальности. Другим обычным приложением процедуры подгонки распределения является проверка гипотезы нормальности до того, как использовать какой-либо параметрический тест (см. выше).
Все права на материалы электронного учебника принадлежат компании StatSoft
Что стандартное отклонение говорит нам в ненормальном распределении
В нормальном распределении правило 68-95-99.7 придает стандартному отклонению большой смысл, но что будет означать стандартное отклонение в ненормальном распределении (мультимодальное или перекошенное)? Будут ли все значения данных по-прежнему находиться в пределах 3 стандартных отклонений? Есть ли у нас правила типа 68-95-99.7 для ненормальных распределений?
Стандартное отклонение является одной конкретной мерой отклонения. Есть несколько других, средняя абсолютная девиация довольно популярна. Стандартное отклонение ни в коем случае не является особенным. Что делает его особенным, так это то, что распределение Гаусса является особенным.
Характеристическая функция нормального распределения определяется всего двумя моментами: средним и дисперсией (или стандартным отклонением). Поэтому для нормального распределения особенно важно стандартное отклонение, оно составляет 50% от его определения.
Для других распределений стандартное отклонение в некоторых отношениях менее важно, потому что у них есть другие моменты. Тем не менее, для многих дистрибутивов, используемых на практике, первые несколько моментов являются самыми большими, поэтому они являются наиболее важными из них, которые нужно знать.
Теперь, интуитивно, среднее говорит вам, где центр вашего распределения, а стандартное отклонение говорит вам, как близко к этому центру находятся ваши данные.
Стандартное отклонение выборки является мерой отклонения наблюдаемых значений от среднего значения в тех же единицах измерения данных. Нормальное распределение или нет.
Почему с нормальным распределением не все нормально
Нормальное распределение (распределение Гаусса) всегда играло центральную роль в теории вероятностей, так как возникает очень часто как результат воздействия множества факторов, вклад любого одного из которых ничтожен. Центральная предельная теорема (ЦПТ), находит применение фактически во всех прикладных науках, делая аппарат статистики универсальным. Однако, весьма часты случаи, когда ее применение невозможно, а исследователи пытаются всячески организовать подгонку результатов под гауссиану. Вот про альтернативный подход в случае влияния на распределение множества факторов я сейчас и расскажу.
Краткая история ЦПТ. Еще при живом Ньютоне Абрахам де Муавр доказал теорему о сходимости центрированного и нормированного числа наблюдений события в серии независимых испытаний к нормальному распределению. Весь 19 и начало 20 веков эта теорема послужила ученым образцом для обобщений. Лаплас доказал случай равномерного распределения, Пуассон – локальную теорему для случая с разными вероятностями. Пуанкаре, Лежандр и Гаусс разработали богатую теорию ошибок наблюдений и метод наименьших квадратов, опираясь на сходимость ошибок к нормальному распределению. Чебышев доказал еще более сильную теорему для суммы случайных величин, походу разработав метод моментов. Ляпунов в 1900 году, опираясь на Чебышева и Маркова, доказал ЦПТ в нынешнем виде, но только при существовании моментов третьего порядка. И только в 1934 году Феллер поставил точку, показав, что существование моментов второго порядка, является и необходимым и достаточным условием.
ЦПТ можно сформулировать так: если случайные величины независимы, одинаково распределены и имеют конечную дисперсию отличную от нуля, то суммы (центрированные и нормированные) этих величин сходятся к нормальному закону. Именно в таком виде эту теорему и преподают в вузах и ее так часто используют наблюдатели и исследователи, которые не профессиональны в математике. Что в ней не так? В самом деле, теорема отлично применяется в областях, над которыми работали Гаусс, Пуанкаре, Чебышев и прочие гении 19 века, а именно: теория ошибок наблюдений, статистическая физика, МНК, демографические исследования и может что-то еще. Но ученые, которым не достает оригинальности для открытий, занимаются обобщениями и хотят применить эту теорему ко всему, или просто притащить за уши нормальное распределение, где его просто быть не может. Хотите примеры, они есть у меня.
Коэффициент интеллекта IQ. Изначально подразумевает, что интеллект людей распределен нормально. Проводят тест, который заранее составлен таким образом, при котором не учитываются незаурядные способности, а учитываются по-отдельности с одинаковыми долевыми факторами: логическое мышление, мысленное проектирование, вычислительные способности, абстрактное мышление и что-то еще. Способность решать задачи, недоступные большинству, или прохождение теста за сверхбыстрое время никак не учитывается, а прохождение теста ранее, увеличивает результат (но не интеллект) в дальнейшем. А потом филистеры и полагают, что «никто в два раза умнее их быть не может», «давайте у умников отнимем и поделим».
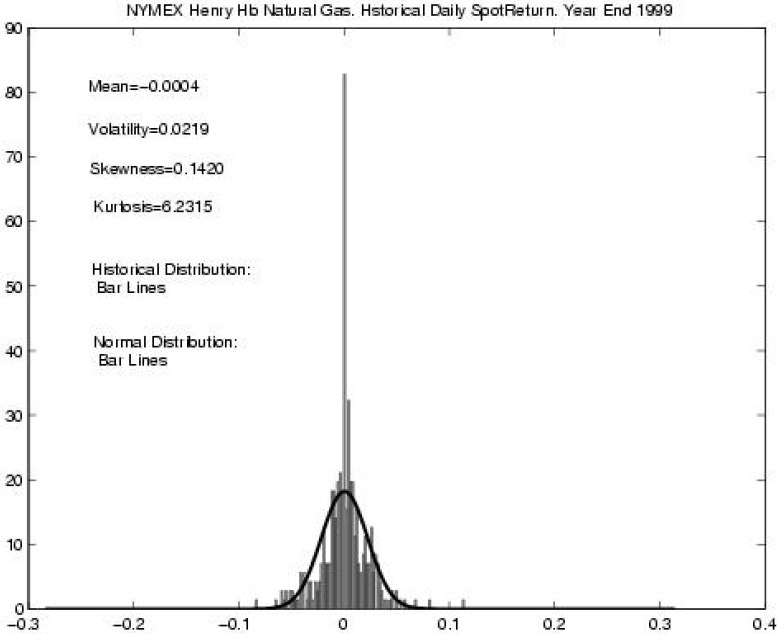
Второй пример: изменения финансовых показателей. Исследования изменения курса акций, котировок валют, товарных опционов требует применения аппарата математической статистики, а особенно тут важно не ошибиться с видом распределения. Показательный пример: в 1997 году нобелевская премия по экономике была выплачена за предложение модели Блэка — Шоулза, основанной на предположении нормальности распределения прироста фондовых показателей (так называемый белый шум). При этом авторы явно заявили, что данная модель нуждается в уточнении, но всё, на что решилось большинство дальнейших исследователей – просто добавить к нормальному распределению распределение Пуассона. Здесь, очевидно, будут неточности при исследовании длинных временных рядов, так как распределение Пуассона слишком хорошо удовлетворяет ЦПТ, и уже при 20 слагаемых неотличимо от нормального распределения. Гляньте на картинку снизу (а она из очень серьезного экономического журнала), на ней видно, что, несмотря на достаточно большое количество наблюдений и очевидные перекосы, делается предположение о нормальности распределения.
Весьма очевидно, что нормальными не будет распределения заработной платы среди населения города, размеров файлов на диске, населения городов и стран.
Общее у распределений из этих примеров – наличие так называемого «тяжелого хвоста», то есть значений, далеко лежащих от среднего, и заметной асимметрии, как правило, правой. Рассмотрим, какими еще, кроме нормального могли бы быть такие распределения. Начнем с упоминаемого ранее Пуассона: у него есть хвост, но мы же хотим, чтобы закон повторялся для совокупности групп, в каждой из которых он наблюдается (считать размер файлов по предприятию, зарплату по нескольким городам) или масштабировался (произвольно увеличивать или уменьшать интервал модели Блэка — Шоулза), как показывают наблюдения, хвосты и асимметрия не исчезают, а вот распределение Пуассона, по ЦПТ, должно стать нормальным. По этим же соображениям не подойдут распределения Эрланга, бета, логонормальное, и все другие, имеющие дисперсию. Осталось только отсечь распределение Парето, а вот оно не подходит в связи с совпадением моды с минимальным значением, что почти не встречается при анализе выборочных данных.
Распределения, обладающее необходимыми свойствами, существуют и носят название устойчивых распределений. Их история также весьма интересна, а основная теорема была доказана через год после работы Феллера, в 1935 году, совместными усилиями французского математика Поля Леви и советского математика А.Я. Хинчина. ЦПТ была обобщена, из нее было убрано условие существования дисперсии. В отличие от нормального, ни плотность ни функция распределения у устойчивых случайных величин не выражаются (за редким исключением, о котором ниже), все что о них известно, это характеристическая функция (обратное преобразование Фурье плотности распределения, но для понимания сути это можно и не знать).
Итак, теорема: если случайные величины независимы, одинаково распределены, то суммы этих величин сходятся к устойчивому закону.
Теперь определение. Случайная величина X будет устойчивой тогда и только тогда, когда логарифм ее характеристической функции 
где 
В самом деле, ничего сильно сложного здесь нет, просто надо объяснить смысл четырех параметров. Параметры сигма и мю – обычные масштаб и смещение, как и в нормальном распределении, мю будет равно математическому ожиданию, если оно есть, а оно есть, когда альфа больше одного. Параметр бета – асимметрия, при его равенстве нулю, распределение симметрично. А вот альфа это характеристический параметр, обозначает какого порядка моменты у величины существуют, чем он ближе к двум, тем больше распределение похоже на нормальное, при равенстве двум распределение становиться нормальным, и только в этом случае у него существуют моменты больших порядков, также в случае нормального распределения, асимметрия вырождается. В случае, когда альфа равна единице, а бета нулю, получается распределение Коши, а в случае, когда альфа равна половине, а бета единице – распределение Леви, в других случаях не существует представления в квадратурах для плотности распределения таких величин.
В 20 веке была разработана богатая теория устойчивых величин и процессов (получивших название процессов Леви), показана их связь с дробными интегралами, введены различные способы параметризации и моделирования, несколькими способами были оценены параметры и показана состоятельность и устойчивость оценок. Посмотрите на картинку, на ней смоделированная траектория процесса Леви с увеличенным в 15 раз фрагментом.
Именно занимаясь такими процессами и их приложением в финансах, Бенуа Мандельброт придумал фракталы. Однако не везде было так хорошо. Вторая половина 20 века прошла под повальным трендом прикладных и кибернетических наук, а это означало кризис чистой математики, все хотели производить, но не хотели думать, гуманитарии со своей публицистикой оккупировали математические сферы. Пример: книга «Пятьдесят занимательных вероятностных задач с решениями» американца Мостеллера, задача №11:
Авторское решение этой задачи, это просто поражение здравого смысла:
Такая же ситуация и с 25 задачей, где даются ТРИ противоречащих ответа.
Но вернемся к устойчивым распределениям. В оставшейся части статьи я попытаюсь показать, что не должно возникать дополнительных сложностей при работе с ними. А именно, существуют численные и статистические методы, позволяющие оценивать параметры, вычислять функцию распределения и моделировать оные, то есть работать так же, как и с любым другим распределением.
Моделирование устойчивых случайных величин. Так как все познается в сравнении, то напомню сначала наиболее удобный, с точки зрения вычислений, метод генерирования нормальной величины (метод Бокса – Мюллера): если 

получится стандартная нормальная величина.
Теперь зададим заранее альфу и бету, пусть V и W, независимые случайные величины: V равномерно распределена на 



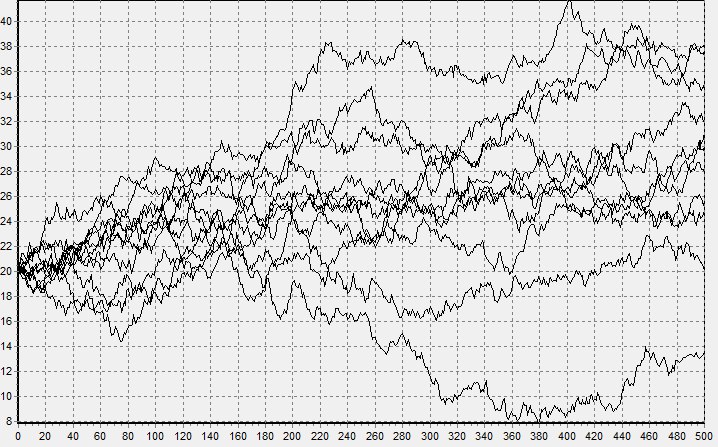
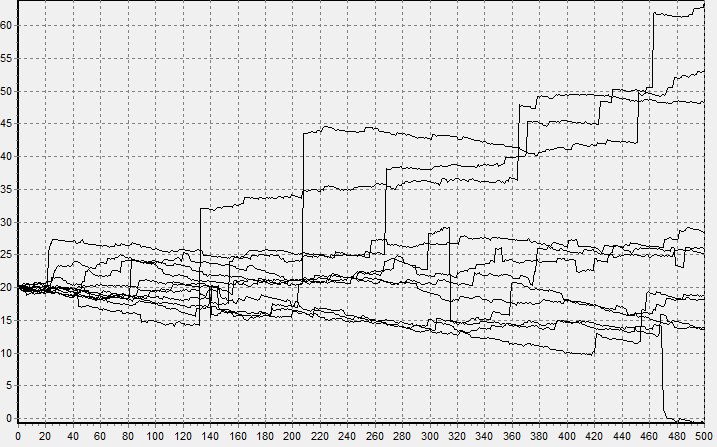
получим устойчивую случайную величину, для которой мю равна нулю, а сигма единице. Это так называемая стандартная устойчивая величина, которую для общего случая (при альфа не равном единице), просто достаточно помножить на масштаб и прибавить смещение. Да, соотношение сложнее, но оно все равно достаточно простое, чтобы его использовать даже в электронных таблицах (Ссылка). На рисунках снизу показаны траектории моделирования модели Блэка — Шоулза сперва для нормального, а затем для устойчивого процесса.
Можете поверить, график изменения цен на биржах больше похож на второй.
Оценка параметров устойчивого распределения. Так как вставлять формулы на хабре достаточно сложно, я просто оставлю ссылку на статью, где подробно разбираются всевозможные методы для оценки параметров, или на мою статью на русском языке, где приводятся только два метода. Также можно найти замечательную книгу, в которой собрана вся теория по устойчивым случайным величинам и их приложениям (Zolotarev V., Uchaikin V. Stable Distributions and their Applications. VSP. M.: 1999.), или ее чисто научный русский вариант (Золотарев В.М. Устойчивые одномерные распределения. – М.: Наука, Главная редакция физико-математической литературы, 1983. – 304 с.). В этих книгах также присутствуют методы для вычисления плотности и функции распределения.
В качестве заключения могу лишь порекомендовать, при анализе статистических данных, когда наблюдается асимметрия или значения, сильно превосходящие ожидаемые, спрашивать самих себя: «правильно ли выбран закон распределения?» и «а все ли с нормальным распределением нормально?».