чем счеты лучше калькулятора
Калькулятор больше не нужен — достаем из шкафа счеты
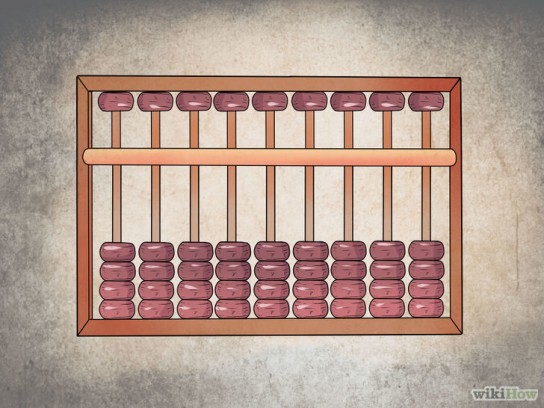
Счеты — это простое счетное устройство, которое впервые применили древние греки и римляне. Счеты состоят из нескольких рядов бусин, нанизанных на проволоку. Бусины первого ряда обозначают единицы, бусины второго ряда — десятки, бусины третьего ряда — сотни и так далее.
Иногда римляне использовали для счета мелкие камни. Они называли их «calculi» — отсюда и произошло современное слово «калькулятор».
Удивительно, но в наш компьютерный век на Ближнем Востоке и в некоторых частях Азии очень популярны обычные бухгалтерские счеты. В то время, когда самые гениальные умы человечества трудятся над созданием космических аппаратов и сверхсовременных вычислительных машин, в Поднебесной многие жители охотно пользуются «суаньпань», именно так китайцы называют счеты. Даже повсеместная компьютеризация не смогла вытеснить из обращения деревянную рамку с подвижными костяшками. Любой кассир китайского магазина так виртуозно владеет мастерством счета на этом, казалось бы, примитивном приспособлении, что можно только позавидовать. Причем, отдают они предпочтение счетам не из бедности и невозможности купить более современный прибор. Они уверены, что простые математические операции гораздо удобнее производить на счетах, чем на вычислительной технике. Счеты имеют еще одно существенное преимущество: они не излучают радиацию, не требуют электроэнергии и не ловят вирусы. Как видим, плюсов действительно немало. В Китае есть даже Ассоциация любителей счетов. В ней миллионы жителей страны ежегодно сдают экзамены по умению владеть таким не хитрым предметом как счеты. Причем, в числе слушателей этих курсов много кассиров и банковских служащих. В школах о счетах также не забывают, уже в начальных классах дети учатся пользоваться ими. Китайцы уверены, что дети, знакомые со счетами, гораздо умнее своих сверстников, привыкших считать на компьютерах и калькуляторах.
Есть сведения, что счетами в Китае пользовались еще в VI веке нашей эры, в XIII столетии они имели уже привычную для нас форму – прямоугольник с натянутыми нитями и костяшками. Позднее «суаньпань» попали в Японию, где их называют «сорабан». Кстати, японцы тоже относятся к счетам с уважением. На рубеже XX и XXI веков в Японии произошло очень любопытное соревнование. В нем участвовал американец с компьютером и японец с обычными счетами. Победить в скорости американец смог только в умножении, а в сложении, вычитании и делении сильнее был представитель Японии. Производители счетов в Китае на отсутствие спроса не могут пожаловаться. На рынок поступает огромный ассортимент продукции. Счеты достойно конкурируют с электронными соперниками.
Источник
Античные счёты — слово из 4 букв в ответах на сканворды, кроссворды
Немного исторических фактов
Счёты являются тем устройством, с которого и начиналась вся история вычислительных предметов. Ещё много столетий назад счёты пользовались мировой популярностью.
Первое вычислительное устройство именовалось «счётной доской». Особенности его использования практически не отличались в различных странах, а вот для изготовления счётов использовались различные материалы.
Что касается времён Древней Руси, то вычисления на первых порах производились посредством использования специальных косточек, группируемых в виде своеобразных кучек. В последующем произошла трансформация счётов, которые обзавелись дощатым видом. Первые счёты были представлены деревянной рамой с верёвочками, на которые нанизывались ягодные косточки.
Именно от последнего внешнего вида вычислительных предметов и отталкивались специалисты, разработавшие те счёты, которые известны практически каждому человеку.
С момента появления эти приспособления стали необычайно популярны, ведь они активно применялись во всех местах, связанных с финансами и необходимостью проведения вычислительных операций. Во времена Советского Союза практически каждый человек владел навыками работы со счётами.
Русские счеты — история
Итак, что это такое? Русские счеты — это простейшее механичное устройство для осуществления вычислений. Это сложение, вычитание, деление и умножение. Имеют место две теории появления счет на Руси:
Как оно было на самом деле, история умалчивает. Но «дощаный» счет до середины XVII века (пока не победил) конкурировал с европейской системой счета на линованных досках типа абак, где он происходил при помощи камешков или специальных жетонов.
Как считать?
Образец – это старые деревянные счеты. Они имеют 12 поперечных проволочек-прутов (РР отделяет 8 верхних от 3 нижних) с десятью костяшками белого цвета, кроме двух черных посередине на 11 из них (на РР – 4 костяшки). Таким образом, русские счеты могут зафиксировать любое число до 10 миллионов. А если исключить РР, то до 10 миллиардов.
Итак, как считать на счетах? Откладывание чисел производится перемещением костяшек из правого в левое положение, а при наборе слева 10 косточек – они убираются в исходное положение. В следующем разряде в левое положение переводится всего лишь одна косточка. РР отделяет целые числа (сверху) от их соответственно десятых, сотых и тысячных долей и в расчетах участие не принимает (ранее использовался для учета «полушек», которая равнялась ½ «деньги» или ¼ копейки).
Счеты бухгалтерские
Они получили массовое распространение в XIX-XX веках, пока их не вытеснили ЭКВМ (электронно-клавишные вычислительные машины). Кстати, этого не смогли сделать арифмометры, которые считали намного быстрее, но работа на них требовала специальной и довольно сложной подготовки по овладению навыками работы на них, в отличии от счет, обучить работе на которых было в разы легче и быстрее.
Вообще-то искусство работы на бухгалтерских счетах и состоит в том, чтобы знать все способы достижения точного результата действий путем разложения общего на частные более легкие операции. Например, умножение на 25 заменяется умножением на 100 и двукратным последовательным делением результата на 2. Или, как умножение, так и деление на любую степень числа 2 производится последовательным соответствующим действием, число которых равно этой степени.
Как считать на счетах? Другой пример. Умножение на двузначное число из одинаковых цифр «АА» (11, 22 и так далее) заменяется умножением на «А» с переносом результата на разряд вверх (умножение на 10) и сложения этой суммы с предыдущей. От опыта и подготовки человека, работающего на счетах, метода его обучения и зависит скорость вычислений, а также применение им специальных приемов.
Сложение на счетах – самая легкая операция. Набирается первое число, потом к нему добавляются костяшки, обозначающее третье и так далее. Надо соблюдать только одно условие. При нехватке косточек для перемещения их в левый ряд – именно столько косточек необходимо оставить в этом ряду, после чего и переместить одну костяшку влево на верхнем пруте. Выполнение происходит сверху вниз (профессионалы могут и наоборот) и складываются только равные разряды (единицы с единицами, десятки с десятками и так далее).
Как выполняется вычитание на счетах? Помня, что счеты не работают с отрицательными числами, всегда надо иметь в виду, что вычитание производится из числа более крупного. А если надо сделать наоборот, то все-таки меньшее вычитается из большего, а знак запоминается или записывается. Вычитание на русских счетах производится сверху-вниз, то есть от высших разрядов к низшим. На соответствующей проволоке отбрасывается вправо необходимое число косточек и если их не хватает, то одна косточка переносится вправо в старшем разряде, а на данной проволочке все переносится влево и из них убирается вправо необходимое число.
Теперь про умножение на счетах. Древние счеты способствуют повышению скорости проведения действий по умножению, которая значительно превосходит скорость осуществления тех же действий на бумаге. На практике умножение – это многократное сложение искомого с самим собой в числовом выражении. Несколько советов:
Способы, упрощающие процесс умножения:
Как умножение заменяется многократным сложением, так и деление на счетах – это постоянное вычитание. Начинается все с верхнего разряда и идет вниз. Переносится направо число косточек, равных делителю (каждый раз, как это удается на самой верхней проволочке, переносится одна косточка налево) до тех пор, пока слева не окажется косточек меньше чем число, на которое производится деление (делитель).
Затем к процессу подключается нижеследующий разряд. И если в предыдущей проволочке остались косточки, то вычитается делитель уже из двузначного числа. Если нет, то, как в предыдущий раз. Если в низшем разряде вычитание пройдет без остатка косточек слева, то значит деление произведено без остатка. Если слева косточки остались, то в случае необязательного получения в итоге дробного числа – остаток игнорируется, а если обязательно его получение, то вычитание продолжается до нужной точности на прутьях ниже РР, с указанием дробного разделителя на бумаге. Аналогично производится деление на двухзначные, трехзначные (и т. д.) числа, только сначала вычитание идет из соответственно двух, трех и так далее высших разрядов.
Способы, упрощающие процесс деления:
На протяжении четверти тысячелетия популярности и практической необходимости счет неоднократно предпринимались (часто закончившиеся удачно), попытки усовершенствовать русские счеты. Остановимся только на одной из них. В 1828 г. генерал-майор Ф. М. Свободский представил в соответствующую инстанцию счетный прибор, который не только осуществлял привычные для русских счет действия, но достаточно быстро извлекал кубические корни, возводил числа в степень, вычислял сложные проценты и так далее. Достигалось это только методами сложения и вычитания с фиксацией промежуточных результатов на специальном поле счет. Однако скорость получения искомого результата так поразила комиссию, что она рекомендовала данный прибор к производству и введению специального курса в военных заведениях. Но до реального исполнения решения дело не дошло.
В настоящее время в России счеты применяются только в качестве музейного экспоната или семейной реликвии. Очень редко, если они наличествуют у кого-то в доме, могут использоваться подрастающим поколением для катания по полу, или старшими для массажа ног или спины. А зря! В современном Китае на «Суаньпань» учат учеников младших классов, так как считается, что освоивший такой способ счета ребенок развивается лучше и быстрее, не научившегося работать на этом древнем приспособлении.
Абак в разных регионах.
Абак впервые появился, возможно, в Древнем Вавилоне. 3 тыс. лет до н. э. Изначально являл собой доску, которая разграфлена на полосы или с углублениями. Счётные метки (косточки, камешки) передвигались по углублениям, линиям. В Египте в V в. до н. э. вместо углублений и линий стали применять палочки и проволоку с нанизанными камешками.
Абак применяли и народы Индии. Арабы с абаком знакомились у народов, подчинённых ими. В заглавиях большинства арабских руководств по арифметике есть слова, имеющие корень «пыль».
У индийцев, как и у восточных арабов абак скоро был вытеснен индийской нумерацией, однако он крепко держался у западных арабов, которые захватили в конце VIII века и Испанию. В X веке тут со счётом на абаке познакомился француз Герберт (940—1003), который написал об этом книгу (980—982) и пропагандировал через своих учеников и сам использование абака. При счёте на абаке вместо камешков использовались и жетоны с числовыми знаками, начертанными на них или римскими цифрами, или особенными числовыми знаками — апексами. По форме апексы Герберта близки к цифрам гобар западных арабов. Апексы Герберта и 27-колонный абак, предмет удивления современников (воссозданы в реставрированном виде по разным рукописям профессором Бубновым Н. М., профессором истории из Киевского университета, начало XX века). Усилиями многих учеников и последователей Герберта и при помощи его влияния, как папы римского (Сильвестра II, 999—1003) абак имеет широкое распространение в Европе. Следы данного распространения удержались, между прочим, в разных языках. Английский глагол обозначает графить — словом от такого же корня называют клетчатую материю, the cheque, или check — банковый чек, exchequer — казначейство. Последний термин проходит от того, что в банке расчёты производились на абаке, основание которого было в разграфлённой доске. Государственное английское казначейство называлось до последнего времени Палатой шахматной доски — по клетчатому сукну, которым покрывался стол заседаний. Клетчатая скатерть была абаком при вычислениях. Палата шахматной доски, которая возникла в XII веке была до 1873 года финансовым верховным управлением и высшим судом по финансовым вопросам.
В Европе абак использовался до XVIII века. В Средние века сторонники производства арифметических вычислений только с помощью абака — абацисты — в течение нескольких столетий проводили ожесточённую борьбу с алгоритмиками — приверженцами появившихся тогда методов алгоритмизации арифметических действий.
Ацтекские счёты появились примерно в X веке и изготавливались из кукурузных зёрен, которые нанизывались на струны, которые установлены в деревянной раме.
В Империи инков использовалось счётное устройство юпана (в паре с кипу), которая имела разновидности: геоюпана, арифметическая юпана и др. В юпане, судя по всему, применялась фибоначчиева система счисления.
В странах Востока имеется китайский аналог абака — японский и суаньпань — соробан. Конструкции аналогичны, применяют десятичную систему счисления, хотя японский вариант чуть экономичнее (в китайском, как и в русских счётах, применяются «лишние» косточки с точки зрения математики). Для японского и китайского абака есть скрупулёзно разработанный набор алгоритмов, которые позволяют механически (то есть не занимаясь добавочными вычислениями на бумаге или в уме) исполнять все четыре арифметических действия и извлекать даже кубические и квадратные корни.
Японский соробан активно применяется по сей день, невзирая на повсеместное распространение электронных калькуляторов. В Японии применение соробана — элемент школьной программы обучения в младших классах счёту. В Японии и странах, которые имеют большую японскую диаспору, Также счёт на соробане известен как своеобразный спорт или тип развлечения.
Русские счеты или десятичный абак, в которых применяется десятичная система счисления и возможность использовать четверти, десятые и сотые дробными долями возникли в России на рубеже XV — XVI веков и применялись активно в торговле до последнего десятилетия XX века. Счеты от классического абака отличаются увеличением разрядности всех числовых рядов и конструкцией. Ещё одна особенность русских счёт — выделенный специально разряд для счёта в четвертях. С момента своего появления счеты почти не менились.
С появлением электронных дешёвых калькуляторов счёты почти полностью вышли из применения. Ещё ранее, в начале 1980-х годов, обучение использованию счётами исключено из школьной программы в СССР.
Какие же инструменты помогали человечеству?
Древние люди делали зарубки на костях и камнях и носили эти палочки с собой, либо оставляли чёрточки на стенах жилищ. Одно из самых старинных устройств, которое не так уж далеко ушло от костей на полу пещеры — это, конечно, счёты. По сути они представляют собой те же кости (деревяшки, камушки), только нанизанные на спицы, которые закреплялись в раме.
Их близкий родственник — счётная доска абак, которая появилась в Вавилоне около пяти тысяч лет назад. Очевидно, что её появлению мы обязаны бурной вавилонской торговле. Если классические счёты, какими их знают в России, опираются на позиционную десятичную систему счисления, то вавилонский абак использовал шестидесятеричную. Такой оригинальный способ счёта происходит, как и большинство систем счисления, от пропорций человеческого тела — если говорить точнее, от числа фаланг пальцев на одной руке (не считая большого).
Вариации счётных досок были во всех древних культурах. В Японии они называются соробан, в Китае — суньпань. Римляне делали счёты из металла, передвигая костяшки в пазах металлической доски, а ацтеки — из кукурузных зёрен. Инки использовали для подсчёта зёрен «многоэтажное» устройство под названием юпана.
Как развивались счётные машины?
В общем виде счётная машина представляет собой устройство, работающее на зубчатых колёсах и цилиндрах, которое производит четыре основных математических действия. Записывающие счётные машины также могут автоматически фиксировать результаты на ленте. Принцип счёта основан на поразрядном сложении и сдвиге суммы частных произведений. Свои версии арифмометра создали Блез Паскаль, спроектировавший в 1646 году суммирующую машину «паскалина», и Готфрид Вильгельм Лейбниц: в его арифмометре была ручка, вращение которой ускоряло повторяющиеся операции.
Также следует упомянуть вычислительную машину, разработанную Чарльзом Бэббиджем в XIX столетии. Она могла производить вычисления с точностью до двадцатого знака, подходила для операций с логарифмами и тригонометрическими функциями. Программа для неё была составлена Адой Лавлейс, первой женщиной-программистом, да и вообще первым программистом в мире. Именно ей принадлежат термины «цикл» и «рабочая ячейка».
Электронный прорыв
Настоящий прорыв в развитии вычислительной техники случился в 60-х годах ХХ века.
В 1957 году японская компания Casio выпустила первый полностью электронный калькулятор 14-А. Событие было эпохальным, потому что открыло новую эру в мире счёта, но жизнь офисных работников и инженеров эта модель не изменила, ведь весил калькулятор целых 140 кг.
Первым компактным, а значит, массовым, калькулятором стал Anita, выпущенный английской компанией Bell в 1961 году. Он работал на газоразрядных лампах и был оснащён клавишами ввода числа и множителя. С тех пор функции калькуляторов становились всё более серьёзными, а сами калькуляторы — всё более лёгкими и умными.
Например, в 1965 году появился первый настольный электронный калькулятор со встроенной памятью Casio 001. Весил он всего 17 килограмм, что по тем временам для машины, способной запоминать операции, было вовсе не много, а два года спустя появился первый настольный программируемый калькулятор Casio AL-1000.
Однако пользователям калькуляторов было и этого мало, ведь счётное устройство куда удобнее держать в руке и носить с собой. Так появились калькуляторы Sharp и Canon, которые весили менее килограмма.
Жителям России особенно запомнились калькуляторы фирмы «Электроника»: шрифт, которым написано это слово, по сей день вызывает ностальгию у бывших советских граждан.
Вот ещё несколько эпохальных инноваций от японской марки Casio, которые существенно изменили представления о том, на что способны калькуляторы.
Появился карманный калькулятор Casio Mini, продажи которого побили все рекорды. А через некоторое время компания выпустила миниатюрную версию, Casio Mini Card, размером с кредитную карту.
Компания выпустила калькулятор FX-7000G — первый в мире программируемый графический калькулятор, доступный широкой публике, с матричным дисплеем, имеющем разрешение 96×64 пикселя. Эта модель может отображать как встроенные графики, так и построенные пользователем. В дополнение к режиму графического отображения калькулятор имеет функцию программирования на языке Бейсик.
Пять лет спустя на прилавках появился калькулятор Casio CFX-9800G, в котором впервые появилась возможность делать графики в разных цветах. По сути, был добавлен цветной дисплей. В отличие от современных экранов, он был трёхцветным и работал на отражённом свете. Это дало возможность рисовать каждый график своим цветом, что делало графические отображения функций куда более наглядными.
Casio выпускает устройство CASIO ClassPad 300 — первый калькулятор с большим сенсорным экраном. Модель имела систему компьютерной алгебры (CAS), которая позволяет производить преобразования выражений в аналитической (символьной) форме.
2004 год.появился калькулятор Casio FX-82ES с технологией Natural Display, позволяющий вводить выражения в естественном виде так, как они выглядят на бумаге. Например, вводить обыкновенные дроби, квадратные корни, экспоненты и логарифмы в виде, принятом в учебниках. В результате сокращается количество ошибок в вычислениях, время вычислений и повышается заинтересованность учеников
Модель калькулятора Casio fx-CG20 PRIZM явилась развитием первой модели, выпущенной в 2010 году. В отличие от предшественников она имела полноцветный экран высокого разрешения. Модель, несмотря на экран с подсветкой, не потеряла в энергоэффективности и способна месяцами работать на одном комплекте батарей.
Сейчас калькуляторы не только стали компактными и лёгкими, но и освоили массу функций, которые могут быть полезны всем, кому требуются точные и сложные расчёты. Сейчас существуют научные калькуляторы, которым под силу производить вычисления с дробями, считать векторы и матрицы, совершать метрические преобразования и решать уравнения, графические калькуляторы, позволяющие создавать таблицы и строить графики по картинке, а также финансовые калькуляторы, которые справляются с расчётом облигаций и другими нуждами финансиста.
На сегодняшний день флагманская графическая модель — калькулятор Casio FX-CG50 с цветным экраном высокого разрешения, возможностью строить 3D графики, режимом программирования, а также поддержкой векторных и матричных вычислений.
Доэлектрический счёт: от пальцев к арифмометрам
У современного человека есть потрясающие инструменты для работы с числами: смартфоны, планшеты, калькуляторы, компьютеры и т.д. Калькуляторы (как отдельные устройства) считаются архаизмом и используются редко, например, в офисах и образовательных учреждениях. Для большинства людей калькулятор – это иконка в дальней папке телефона, про которую вспоминают, когда надо посчитать зарплату или разделить счёт в ресторане.
Однако пару сотен лет назад за современный калькулятор могла бы развернуться настоящая война. Тем не менее людям нужно было считать задолго до их появления.

В журнале Nature Communications опубликована статья, в которой исследователи из США выяснили, что обезьяны интуитивно понимают числа и способны различать количество объектов независимо от их размеров.
Поэтому напрашивается вывод, что люди считали ещё в те времена, когда не знали, что такое счёт или изопериметрические неравенства в математической физике.

Но уж если человек берётся за какое-то дело, то всегда ищет способы его оптимизировать: ускорить, потратить меньше ресурсов, сделать качественнее и точнее. Так появились первые инструменты счёта.
История инструментов счёта
Содержание:
Чем богаты, тем и рады
Первый инструмент лежал буквально перед глазами. Настолько буквально, что это наши руки 🙂
Если повторить за картинкой, то может пойти дождь.
Счёт на пальцах оставался широко распространённым в древнем мире вплоть до конца средневековья. С развитием торговли людям понадобилось считать бóльшее количество объектов, тогда появилась, возможно, первая разрядность: 5 – “одна рука”, 10 – “две руки”, 20 – “один человек”. Таким образом древние народности научились считать вещи в “людях”. К пальцам “одного человека” можно прибавить пальцы “второго”, “третьего” и т.д.
Цивилизация индейцев майя называла данную систему счисления двадцатичной. Вероятно, количество пальцев на руках подарило нам десятичную систему счисления.
Все народы на этапах своего становления так или иначе вели простейшие математические операции, поэтому появилось огромное разнообразие способов счёта на пальцах.

Как пример, рассмотрим ситуацию, когда возникает недопонимание у людей разных национальностей.
Английский счёт
В большинстве англоязычных стран люди ведут счёт разжатием пальцев из кулака, где пятерка соответствует большому пальцу. Прямо как у нас, японцев и людей из балканского региона на юго-востоке Европы.

В фильме Квентина Тарантино “Бесславные ублюдки” обыгрывается разница между счётом у англичан и немцев. Когда в баре британский военный (играет Майкл Фассбендер) под прикрытием заказывает выпивку и показывает указательным, средним и безымянным пальцами число три, другой военный – офицер фашистской Германии (Аугуст Диль) – сразу же раскрывает его. После начинается перестрелка в лучших традициях Тарантино.
Отсюда вопрос: как заказать виски в Германии, чтобы не попасть в перестрелку?
Континентальный европейский счёт
Именно этот счёт используют немцы, французы и другие народы континентальной западной Европы.

Принцип следующий:
Счёт начинается с большого пальца и указывает на число 1.
Разгибаем указательный (число 2) и т.д. до мизинца (число 5).
На другой руке продолжаем считать аналогично – большой палец соответствует шестерке.
Иногда используется (во Франции и других странах Европы) альтернативный способ, при котором пальцы не разгибают, а загибают.
Простейшие устройства
Тысячи лет назад человечество освоило простейшие счётные устройства. Торговля и хитрость людей (ага, уже тогда пытались продать два бивня мамонта по цене трёх) способствовали созданию инструментов счёта.
Балансирные весы
Стоп, стоп, стоп. Да, весы не позволяют пересчитывать вещи по отдельности, однако торговцам древности не требовалось знать точное количество зёрнышек риса в мешке, достаточно было определить эквивалент этого мешка. И балансирные весы справлялись с этой задачей просто замечательно. Привычные нам весы считаются одним из первых приборов для количественного определения массы.
Абак – семейство счётных досок
В ряде древних культур для арифметических вычислений использовались счётные доски. Как и откуда появился абак – неизвестно, однако, учитывая большое распространение в мире, этот инструмент мог появиться в некой родительской народности, “породившей” все остальные.
В современном мире по-прежнему применяются некоторые варианты абака – русские счёты и японский соробан. В некоторых странах счёты всё ещё в ходу: используются в работе и обучении детей, так как аналоговые приборы надёжны, а их удобство проверено временем.

Сложные устройства
Первые сложные счётные устройства появились в античности вместе с зубчатыми колёсами. Узнать, какой механизм был первым, когда он был произведён – невозможно. Однако в 1901 году на борту затонувшего корабля нашли Антикитерский механизм. Учёные установили, что он был создан приблизительно во II веке до н.э.
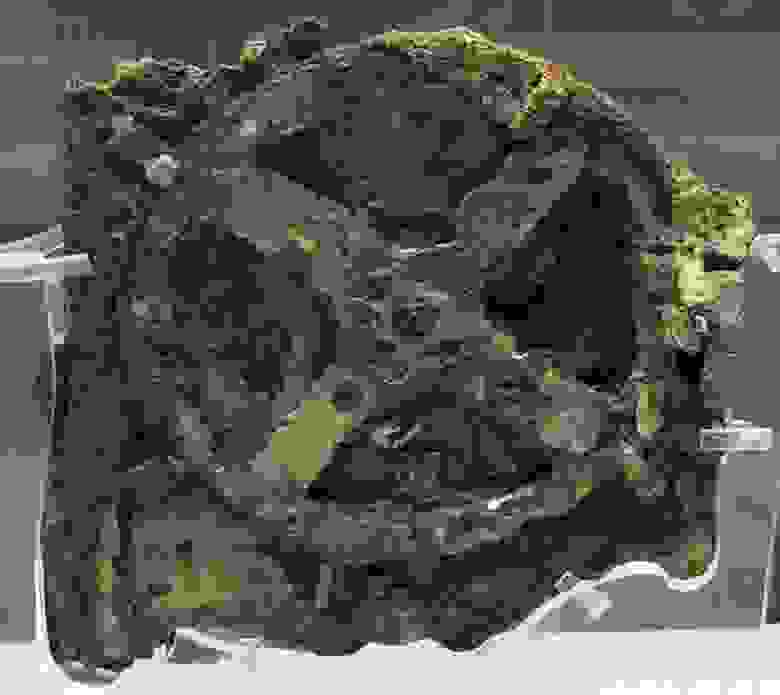
Особенности:
Механизм представляет собой календарь, а также астрономическое, метеорологическое, образовательное и картографическое устройство;
Технология создания была утеряна;
Самый древний образец аналогового вычислительного устройства;
Первая известная механическая Солнечная система, планетарий и астрономические часы.
Потребность в функциональных устройствах имелась всегда, поэтому, несмотря на утерю технологии создания Антикитерских механизмов, люди придумывали другие. Рост сложности расчётов в XVII веке привел к новым изобретениям.
Палочки Непера – быстро забытый восторг
Создал Палочки Непера шотландский математик и отец логарифмов – Джон Непер (1550-1617). Принцип работы изобретения описан в его книге 1617 года.
Особенности:
В основном использовались для сложных действий умножения, реже – деления;
Непер также является одним из изобретателей логарифмов;
Такой инструмент легко сделать самому из обычного листа бумаги, когда использовать калькулятор нет возможности или запрещено (например, на экзамене).
Принцип работы в двух словах
Если вкратце, то инструмент создан для умножения и состоит из 10 длинных прямоугольных палочек. На каждой грани записано число, а ниже – результат его умножения на 1,2,3 и т.д до 9.
Палочка Непера. Попрошу без смешков.
С помощью нескольких палочек можно было умножить большое число, например, 6359 на 5:
Выбираем палочки с этими числами сверху и прикладываем друг к другу;
Пятые квадраты дадут произведение числа на 5;
Складываем эти произведения.
3 (0 + 1) (5 + 2) (5 + 4) 5
Итого получаем: 31795
Когда Палочки Непера только появились, они пользовались большой популярностью, однако совсем скоро на смену им пришел более совершенный инструмент счёта.
Логарифмическая линейка
Первые попытки создать нечто похожее на логарифмическую линейку, предпринял в XVII веке Эдмунд Гюнтер – астроном из Англиии. Он нанёс на классическую линейку шкалу логарифмов и с помощью двух циркулей производил расчёты. Это было сложно, долго и требовало повышенной внимательности.

Параллельно Гюнтеру логарифмическую линейку разрабатывал Уильям Отред (1575-1660), который предложил вместо циркулей две одинаковые шкалы, скользящие вдоль друг друга. Спустя пару лет после смерти Отреда линейку оснастили бегунком и визиром. В таком виде она служит людям и по сей день.
Появление логарифмической линейки было важным событием того времени, так как она давала возможность быстро складывать, вычитать, умножать, делить, возводить в степень, извлекать корень, катапультировать бумажки в других учёных, вычислять логарифмы и работать с тригонометрическими функциями.
Особенности:
До появления карманных калькуляторов этот инструмент служил незаменимым расчётным орудием инженеров и математиков;
Высокая точность расчётов – около 3 значащих цифр;
Каждый хоть раз в жизни видел или держал логарифмическую линейку в руках. На её устройстве и принципе работы останавливаться не будем, так как существует очень много видов линеек с разным функционалом и формой. Для некоторых моделей даже выпускали целые книги-инструкции. Тем, кто желает углубиться или освежить память, оставлю ссылку на подробный материал.

Следующим этапом в развитии счётных инструментов стали сложнейшие механические устройства.
Эпоха арифмометров
Арифмометр – это механическая счётная машина, созданная для математических вычислений. Первые образцы появились ещё в XVII веке, однако есть мнение что Леонардо да Винчи в своих дневниках изобразил первый арифмометр еще в 1492 г.

Доказательств, что на его чертежах был именно механизм счётной машины, а также, что она была создана, не сохранилось. Поэтому сразу перейдём к настоящим арифмометрам.
Считающие часы Вильгельма Шиккарда – нейминг придумали позже
Про это устройство есть отдельная подробная статья на Хабре, желающих – милости прошу.
Считающие часы Вильгельма Шиккарда – первый механизм, способный складывать, вычитать, делить и умножать. До наших дней дошло немного информации о нём, однако известно, что над изобретением в 1623 году трудился немецкий учёный, астроном и математик – Вильгельм Шиккард (1592-1635).
Особенности:
Первая в мире механическая счётная машина, позволяющая складывать, вычитать, делить и умножать числа;
Была известна довольно узкому кругу лиц, и поэтому долгое время (почти 300 лет со дня её изобретения) никто не знал о её существовании.
Работа механизма была основана на использовании взаимосвязанных звёздочек и шестерёнок, из-за конструктивного сходства с часами устройство и получило название “считающие часы”. Друг Шиккарда, философ и астроном Иоганн Кеплер, в письмах получал информацию о практически готовом устройстве, которое впоследствии сгорело в пожаре. Звучит правдоподобно.
Доподлинно неизвестно, была ли создана вторая версия устройства. Вероятно, никто, кроме самого Шиккарда и его механика Вильгельма Пфистера, работающее устройство так и не увидел.
Из-за этих обстоятельств долгое время первым арифмометром считалось изобретение другого учёного.
Паскалина
Паскалина – это механическое складывающее устройство, напоминающее ящик со связанными друг с другом шестёренками.
В 1640 году некий одарённый 17-летний юноша в Руане помогал отцу распределять подати, налоги и пошлины. Наблюдая за бесконечными и невероятно утомительными расчётами отца, работавшего председателем налогового управления, он задумал создать устройство, способное помочь в неудобных традиционных расчетах.
Спустя два года он создаёт свою суммирующую машину – Паскалину. Имя того юноши – Блез Паскаль (1623-1662). Впоследствии он стал классиком французской литературы, одним из основателей математического анализа, теории вероятностей и проективной геометрии.
Особенности:
Первый арифмометр, получивший известность ещё при жизни автора;
Основное назначение – сложение;
Умножение в устройстве выполняется в виде многократного сложения, для деления числа нужно было использовать многократное вычитание.
Принцип работы
По-умолчанию машина складывает введённые поворотными деталями числа. Каждая деталь соответствует десятичному разряду числа и пронумерована от 0 до 9. Чтобы ввести число, нужно было повернуть колёсико до соответствующей цифры. При полном обороте колёсико переносило избыток на соседний разряд, сдвигая соседнюю деталь на 1 позицию. Ответ выводился в окошке сверху.
При желании Паскалина позволяла не только складывать, но и выполнять другие операции, но в таком случае требовалась сложная процедура последовательных сложений и вычитаний.
Изобретение Паскаля вызывало восторг у людей того времени, однако за 10 лет учёный сумел собрать лишь 50 “Паскалин” и продать с дюжину из них. Богатства изобретение ему не принесло, так как стоимость и сложность создания были слишком высоки, а вычислительные способности ограничены.
Калькулятор Лейбница
Такой в карман не положишь.
Калькулятор Лейбница – это счётная машина созданная в 1673 году немецким математиком Готфридом Вильгельмом Лейбницем (1646-1716). Это первое устройство, способное умножать и делить также легко, как складывать и вычитать.
Кстати, про Лейбница есть замечательный лонгрид на Хабре.
Предпосылкой к созданию этого арифмометра послужило знакомство с астрономом Христианом Гюйгенсом. Как Паскаль желал упростить расчёты отца, так и Лейбниц намеревался помочь Гюйгенсу (и себе, разумеется) упростить и ускорить астрономические вычисления.
От идей и набросков до первого прототипа прошло 3 года. Калькулятор впервые “вышел” в свет на заседании Лондонского Королевского общества. Сын маминой подруги в мире арифмометров – не иначе. Последующие несколько лет Лейбниц дорабатывал конструкцию и уже в 1676 году представил в Лондоне предрелизный новый вариант.

Но, как это часто бывает с прототипами, калькулятор не годился для реального применения из-за малой разрядности, а на последующую доработку ушло еще 18 лет. Последний вариант был создан в 1710 году – спустя 40 лет от первой идеи.
Особенности:
Идея ступенчатого валика оказалась весьма плодотворной. Вплоть до конца XIX века конструкция валика совершенствовалась и развивалась различными изобретателями механических машин;
Де-факто, это первый арифмометр, предназначенный для выполнения четырёх арифметических действий, позволяющий использовать 8-разрядное множимое и 9-разрядный множитель с получением 16-разрядного произведения;
Не стал популярным по двум причинам: отсутствие на него устойчивого спроса и конструкционной неточности, влияющей на результат при умножении предельных для него чисел.
Суммирующая машина Якобсона
Суммирующая машина Якобсона – это, вероятно, первая отечественная счётная машина, созданная Евной Якобсоном. Ни документов, ни свидетельств о времени изготовления машины найдено не было, однако удалось установить промежуток благодаря некоторым надписям на корпусе устройства:
Mechanische Rechnungs Mashine (нем. Механическая счетная машина);
Mechina Mechaniszna do Rachunku (польск. Механическая счетная машина);
Zu der Aufgabe des Addirens, Subtantirens, Multiplicirens, und Devidirens von den Nummer Eins biz kann man hier in der Bruchen zertheilen (нем. Для задачи сложения, вычитания, умножения и деления от числа один до тысячи миллионов, и остающееся от деления можно здесь же расчленить на дроби);
Erfunden und verfertigen von dem Hebreer Jawna Jacobson, Uhrmacher und Mechanicis in der Stadt Nieswiez in Lithauen, Gouvernement Minsk (нем. Изобретена и изготовлена Евной Якобсоном, часовым мастером и механиком, в городе Несвиже Литвы, Минское воеводство).
В последней надписи указан город Несвиж, который входил в состав Минского воеводства до 1793 года. Таким образом Суммирующая машина Якобсона была создана не позднее этой даты.
Из особенностей машины можно выделить следующее:
Основные механизмы установлены во внутренней части машины, а на наружной крышке находятся все шкалы и элементы для управления;
Высокая надежность и удобство в управлении, а размещение зубчатых колёс в несколько уровней делало его ещё и компактным;
Внимание к деталям. Доходило до того, что каждая деталь одного разряда была отмечена одинаковым знаком, чтобы при ремонте детали не перепутались;
Совокупность удачных и находчивых решений делает эту машину выдающейся
для своего времени.
Арифмометр Шарля де Кольмара
Шарль Ксавье Тома де Кольмар (1785-1870) – французский бизнесмен и изобретатель первого в мире коммерческого арифмометра.
Принцип работы его изобретения был основан на калькуляторе Лейбница с дальнейшим развитием идеи ступенчатого валика. В 1820 году был создан первый образец, способный умножать, делить, складывать и вычитать. Преимуществом над другими арифмометрами того времени было умение работать с тридцатизначными числами.
Будучи предприимчивым бизнесменом, а в прошлом военным чиновником, Кольмар запатентовал устройство в том же году, однако коммерческим продуктом его изобретение стало только через 20 лет. В 1840 году он представил арифмометр на промышленной выставке во Франции, где занял серебро. Позже, когда удалось наладить производство, цена на арифмометр кусалась – 400 франков за штуку. Всего за год удавалось продать не более 100 машин, однако спрос и конкуренция росли из года в год.
В 1851 году на выставке арифмометр Шарля де Кольмара также уступил первенство вычислительной машине Штаффеля. Компенсировать недостатки изобретения предприниматель решил более активной рекламой – он создал описание устройства и разослал его всей европейской знати, что позволило получить множество наград.
На выставке в Париже в 1855 году Кольмар показал гигантский двухметровый арифмометр, для управления которым требовалось минимум 2 человека. Как вы уже могли догадаться, главный приз ушел другому изобретению из Швеции.
К концу 1870-х спрос на арифмометры значительно вырос, а благодаря большим усилиям Кольмара, его арифмометр стал одним из самых востребованных на рынке.
Особенности:
Основан на принципе арифмометра Лейбница;
В своё время превосходил все известные машины, так как мог оперировать тридцатизначными числами;
Первый коммерческий арифмометр;
Отличался надежностью, укоренился на конторских столах и отлично продавался в течение следующих 90 лет;
За своё изобретение Тома был награжден орденом Почётного легиона.
Вычислительная машина Штаффеля
Вычислительная машина Штаффеля (1814-1884) – арифмометр, созданный Израилем Авраамом Штаффелем. Разработка началась в 1835 году, а уже в 1845 был представлен первый рабочий образец на выставке в Варшаве.
Штаффель родился в бедной еврейской семье, а потому не имел доступа к научным публикациям, где описывались арифмометры других изобретателей. Будучи часовщиком и проживая в Варшаве, он выучил польский язык и получил доступ к научной информации, издаваемой в Царстве Польском. Существует мнение, что эти факты делали арифмометр Штаффеля непохожим на другие разработки.
В 1845 году на выставке в Варшаве Штаффеля наградили серебряной медалью. Этот факт поспособствовал тому, что царский наместник – князь Варшавский, генерал-фельдмаршал Иван Фёдорович Паскевич передал изобретателю 150 рублей для поездки в петербургскую Академию наук.
Академики в Петербурге высоко оценили арифмометр Штаффеля, отмечая, что для умножения не требовалось последовательное складывание. В 1847 году машину показали императору Николаю I, который наградил Штаффеля из бюджета солидной по тем временам суммой в 1500 рублей серебром.
Для понимания приблизительных цен того времени.
А. Вегелин, 25 февраля 1833 г. из села Сретенского.

На полученные деньги Штаффель улучшал изобретение, а уже в 1851 году забрал золотую медаль на большой выставке в Лондоне, обойдя Кольмара с его арифмометром. Несмотря на попытки популяризировать устройство с помощью выставок и прессы, спрос на счётные машины оставался низким, а издержки производства высокими.
К сожалению, арифмометр так и не пошел в массовое производство. Потратив все свои сбережения на изобретения, Штаффель умер в бедности.
Особенности:
Ни один экземпляр машины не сохранился до XXI века;
Конструкция арифмометра известна только по историческим источникам – статьи для прессы, отчёты и решения жюри c выставок;
Разработка заняла 10 лет, а машина не была запатентована;
Не пошла в массовое производство из-за недостатка спроса и финансирования;
Была представлена в Санкт-Петербургской академии наук, где получила широкое признание среди академиков.
Арифмометр Однера
Арифмометр Однера – один из самых популярных арифмометров в мире. Его разработкой занимался российско-шведский механик Вильгодт Теофил Однер (1845-1905).
Интерес к арифмометром появился у Однера в 1871 году после ремонта арифмометра Шарля де Кольмара. Через пару лет он сделал первый опытный образец, а уже в 1877 году получил заказ на 14 штук от Людвига Нобеля – старшего брата учредителя Нобелевской премии Альфреда Нобеля.
В последующие годы Однер запатентовал конструкцию в нескольких странах и к 1890 году наладил промышленное производство в Санкт-Петербурге, а в 1891 году – в Германии. Уже в 1892 году германское производство пришлось продать; после на заводе производили клоны арифмометров под брендом Brunsviga (по названию города Брауншвейга).
В 1917 году грянула Октябрьская революция, под ноги которой попал и завод Однера в Петербурге.
После национализации имущества в России потомки Однера создали новое производство в Швеции – Original-Odhner (“Настоящий Однер”). В 1924 году петербургский завод Однера перенесли в Москву, где и продолжили выпуск клонов под маркой “Феликс”. Подробнее ознакомиться с арифмометром можно в блоге Яндекс.Музея на Хабре или почитать инструкцию к этому аппарату.
Особенности:
Был распространён во всем мире и запатентован во многих странах;
С его появлением зародилось математическое машиностроение, в течение многих десятков лет он был самой распространенной вычислительной машиной;
Только распространение электронных калькуляторов вытеснило арифмометр Однера из всеобщего употребления;
Клоны этой машины выпускались вплоть до второй половины 20 века, в том числе в России.
Наследие
Разумеется, помимо рассмотренных в статье изобретений существовало множество других. В книгах Ю. Л. Полунова “От абака до компьютера” можно ознакомиться с историей счётных инструментов намного подробнее.
Удобный, быстрый и точный счёт был необходим людям, независимо от эпохи и географии. Подобные инструменты стали естественной составляющей эволюции человечества и привели нас к современным ЭВМ.
По хронологии изобретений чётко прослеживается усложнение и новаторство многих идей. Сперва люди начали с элементарного, а пришли к сложным механизмам и не остановились на достигнутом – позже появились машины с перфокартами и изобретения немецкого учёного Конрада Цузе, но это уже совсем другая история.