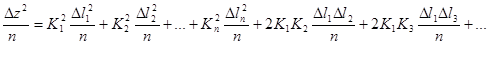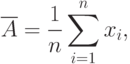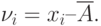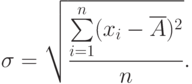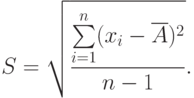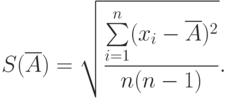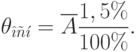чем оценивается точность результатов измерений
ОЦЕНКА ТОЧНОСТИ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Точность результатов многократных измерений одной и той же величины оценивают в такой последовательности.
1. Находят вероятнейшее (наиболее точное для данных условий) значение измеренной величины по формуле арифметической средины х= [l]/п.
2. Вычисляют отклонения δi = li – x каждого значения измеренной величины l1, l2, … ln от значения арифметической средины. Контроль вычислений: [δ] = 0.
3. По формуле Бесселя (19.2) вычисляют среднюю квадратическую погрешность одного измерения.
4. По формуле (19.3) вычисляют среднюю квадратическую погрешность арифметической середины.
5. Если измеряют линейную величину, то подсчитывают относительную среднюю квадратичную погрешность каждого измерения и арифметической средины.
6. При необходимости подсчитывают предельную погрешность одного измерения, которая может служить допустимым значением погрешностей аналогичных измерений.
| № п/п | Время измерения, ч | t1, Cº | t2 Cº | tср= (t1+t2)/2 | d= (t1-t2) | d 2 | Вычисления |
| 12,4 | 12,6 | 12,5 | -0,2 | 0,04 | m =  = 0,17 Сº Mtср= 0,5 = 0,17 Сº Mtср= 0,5 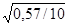 = 0,12 Cº = 0,12 Cº | ||
| 11,7 | 12,0 | 11,8 | -0,3 | 0,09 | |||
| 12,0 | 12,0 | 12,0 | |||||
| 15,1 | 14,7 | 14,9 | +0,4 | 0,16 | |||
| 16,0 | 15,8 | 15,9 | +0,2 | 0,04 | |||
| 20,5 | 20,6 | 20,6 | -0,1 | 0,01 | |||
| 24,9 | 25,2 | 25,0 | -0,3 | 0,09 | |||
| 25,2 | 25,2 | 25,2 | |||||
| 24,4 | 24,2 | 24,3 | +0,2 | 0,04 | |||
| 20,1 | 20,0 | 20,0 | +0,1 | 0,01 | |||
| II | 16,1 | 16,4 | 16,2 | -0,3 | 0,09 | ||
| 13,5 | 13,4 | 13,4 | +0,1 | 0,01 | |||
| ∑= =-0,2 | ∑= =0,58 |
Пример20.1. Длина линии местности измерена шесть раз. Требуется определить вероятнейшее значение длины линии и оценить точность выполненных измерений. Результаты измерений и вычислений записывают по форме, приведенной в табл.20.1.
Пример20.2. На метеостанции температура воздуха измерялась в разное время суток двумя одинаковыми термометрами.
Требуется определить среднюю квадратичную погрешность измерения температуры воздуха одним термометром и среднего значения из одновременных измерений двумя термометрами. Значения измеренных температур воздуха и оценку точности измерений записывают по форме, приведенной в табл. 20.2.
Оценку точности по разностям двукратных измерений производят в такой последовательности. 1. Вычисляют среднее значение из двукратных измерений. 2. Вычисляют разности d двукратных измерений. 3. По формуле (19.4) вычисляют среднюю квадратичную погрешность одного измерения 4,0см. По формуле (19.5) вычисляют среднюю квадратичную погрешность среднего результата из двух измерений.
СРЕДНЯЯ КВАДРАТИЧЕСКАЯ ОШИБКА ФУНКЦИИ
ИЗМЕРЕННЫХ ВЕЛИЧИН
В тех случаях, когда пользуются косвенными методами измерений, ошибка результата зависит как от ошибок измеренных величин, так и действий, с помощью которых вычислен искомый результат. Поэтому определение ошибок функций измеренных величин mf имеет большое практическое значение.
Рассмотрим функцию z самого общего вида от многих независимых величин l1,l2,…,ln:
С учетом ошибок измерений, можно записать
Поскольку Δl1, Δl2, …, Δln малы, то функцию можно разложить в ряд Тейлора, ограничиваясь членами, содержащими только первые степени ошибок Δl1, Δl2, … Δln. При разложении в ряд применяются частные производные, так как в уравнении имеются несколько переменных аргументов.
z + Δz = f(l1, l2, … ln) + ( 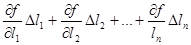
Δz = 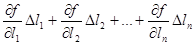
Для удобства записи примем, что

тогда уравнение (21.2) примет вид
Возведем уравнение (21.3) в квадрат и разделим на n
Если выполнен ряд измерений, то можно получить n аналогичных равенств, просуммировав которые можно получить уравнение

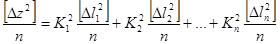
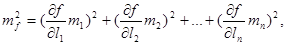
т.е. квадрат средней квадратической ошибки функции общего вида равен сумме квадратов произведений частных производных по каждому аргументу на среднюю квадратическую ошибку соответствующего аргумента.Назад
ГЕОДЕЗИЧЕСКИЕ ИЗМЕРЕНИЯ
ИЗМЕРЕНИЕ ДЛИНЫ ЛИНИЙ
ВВОДНЫЕ СВЕДЕНИЯ
Измерения – процесс сравнения какой-либо величины с другой одноименной величиной, принимаемой за единицу.
Геодезические измерения позволяют определять относительное взаимное расположение отдельных точек земной поверхности. Геодезические измерения бывают: 1)линейными, в результате которых на местности определяются расстояния между заданными точками; 2) угловыми, определяющими значения горизонтальных и вертикальных углов на земной поверхности в данных вершинах между направлениями на некоторые заданные точки; 3) высотными (нивелирование), в результате которых определяются разности высот отдельных точек, т. е. разности расстояний по нормали от принятой отсчетной поверхности до данных точек.
В России для перечисленных видов геодезических измерений используются следующие единицы:
а) в линейных измерениях (горизонтальных и вертикальных) – метр. Эталон длины метра физически реализован в виде однометрового платино-иридиевого жезла № 28, хранящегося во Всероссийском научно-исследовательском институте метрологии;
б) в угловых измерениях – окружность и ее доли – градус, равный 1/360 окружности; минута, равная 1/60 градуса; секунда, равная 1/60 минуты. В некоторых странах, например в ФРГ, применяется градовая (метрическая) система: 1 град, равный 1/400 окружности; 1 минута, равная 1/100 града; 1 секунда, равная 1/100 минуты.
Измерение расстояний производят непосредственным или косвенным методами. При непосредственном методе мерный прибор (измерительную рулетку, землемерную ленту и т. п.) последовательно укладывают в створе измеряемого отрезка. При косвенном методе измеряют вспомогательные параметры (углы, базисы, физические параметры и т. п.), а длину отрезка вычисляют по формуле, отображающей зависимость между измеренными величинами и длиной отрезка. Непосредственно длины отрезков измеряются с помощью механических мерных приборов – мерных лент, рулеток, длинномеров и т. д. Косвенные методы реализуются с использованием различных видов дальномеров – оптических, радиофизических, лазерных и т. д.
Точность определения расстояний зависит от метода измерений, применяемого прибора, условий измерений и колеблется от 1:200 до 1:1000 000 измеряемого расстояния. Назад
Чем оценивается точность результатов измерений
ГОСТ Р ИСО 5725-6-2002
ГОСУДАРСТВЕННЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ТОЧНОСТЬ (ПРАВИЛЬНОСТЬ И ПРЕЦИЗИОННОСТЬ) МЕТОДОВ И РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Использование значений точности на практике
Accuracy (trueness and precision) of measurement methods and results. Part 6. Use in practice of accuracy values
Дата введения 2002-11-01
Предисловие
1 РАЗРАБОТАН Федеральным государственным унитарным предприятием «Всероссийский научно-исследовательский институт метрологической службы» Госстандарта России (ВНИИМС), Всероссийским научно-исследовательским институтом стандартизации (ВНИИСтандарт), Всероссийским научно-исследовательским институтом классификации, терминологии и информации по стандартизации и качеству (ВНИИКИ) Госстандарта России
ВНЕСЕН Управлением метрологии и Научно-техническим управлением Госстандарта России
3 Настоящий стандарт представляет собой полный аутентичный текст международного стандарта ИСО 5725-6:1994* «Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике»
5 ПЕРЕИЗДАНИЕ. Март 2009 г.
* С 1 июля 2007 г. введен в действие ГОСТ Р ИСО/МЭК 17025-2006.
ГОСТ Р ИСО 5725 представляет собой полный аутентичный текст шести частей международного стандарта ИСО 5725, в том числе:
ГОСТ Р ИСО 5725-1-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения»;
ГОСТ Р ИСО 5725-2-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений»;
ГОСТ Р ИСО 5725-3-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений»;
ГОСТ Р ИСО 5725-4-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений»;
ГОСТ Р ИСО 5725-5-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений»;
ГОСТ Р ИСО 5725-6-2002 «Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике».
Пользование частями 2-6 ГОСТ Р ИСО 5725 в отдельности возможно только совместно с частью 1 (ГОСТ Р ИСО 5725-1), в которой установлены основные положения и определения, касающиеся всех частей ГОСТ Р ИСО 5725.
В соответствии с основными положениями ИСО 5725-1 (пункт 1.2) настоящий стандарт распространяется на методы измерений непрерывных (в смысле принимаемых значений в измеряемом диапазоне) величин, дающие в качестве результата измерений единственное значение. При этом это единственное значение может быть и результатом расчета, основанного на ряде измерений одной и той же величины.
Применяемый в международных стандартах термин «стандартный метод измерений» адекватен отечественному термину «стандартизованный метод измерений».
В ИСО 5725: 1994-1998 и ИСО/МЭК 17025-99 понятие «метод измерений» («measurement method») включает совокупность операций и правил, выполнение которых обеспечивает получение результатов с известной точностью. Таким образом, понятие «метод измерений» по ИСО 5725 и ИСО/МЭК 17025 адекватно понятию «методика выполнения измерений (МВИ)» по ГОСТ Р 8.563-96 «Государственная система обеспечения единства измерений. Методики выполнения измерений» (пункт 3.1) и соответственно значительно шире по смыслу, чем определение термина «метод измерений» в Рекомендации по межгосударственной стандартизации РМГ 29-99 «Государственная система обеспечения единства измерений. Метрология. Основные термины и определения» (пункт 7.2).
Следует отметить, что в отечественной метрологии точность (accuracy) и погрешность (error) результатов измерений, как правило, определяются сравнением результата измерений с истинным или действительным (условно истинным) значением измеряемой физической величины (являющимися фактически эталонными значениями измеряемых величин, выраженными в узаконенных единицах).
В условиях отсутствия необходимых эталонов, обеспечивающих воспроизведение, хранение и передачу соответствующих значений единиц величин, необходимых для оценки погрешности (точности) результатов измерений, и в отечественной, и в международной практике за действительное значение зачастую принимают общее среднее значение (математическое ожидание) установленной (заданной) совокупности результатов измерений. В ИСО 5725 эта ситуация отражена в термине «принятое опорное значение» (см. пункты 3.5 и 3.6 ГОСТ Р ИСО 5725-1) и рекомендуется ГОСТ Р ИСО 5725-1 для использования в этих случаях и в отечественной практике.
В соответствии с ИСО 5725 цель государственных стандартов ГОСТ Р ИСО 5725 состоит в том, чтобы:
а) изложить основные положения, которые следует иметь в виду при оценке точности (правильности и прецизионности) методов и результатов измерений при их применении, а также при планировании экспериментов по оценке различных показателей точности (ГОСТ Р ИСО 5725-1);
б) регламентировать основной способ экспериментальной оценки повторяемости (сходимости) и воспроизводимости методов и результатов измерений (ГОСТ Р ИСО 5725-2);
в) регламентировать процедуру получения промежуточных показателей прецизионности методов и результатов измерений, изложив условия их применения и методы оценки (ГОСТ Р ИСО 5725-3);
г) регламентировать основные способы определения правильности методов и результатов измерений (ГОСТ Р ИСО 5725-4);
д) регламентировать для применения в определенных обстоятельствах несколько альтернатив основным способам (ГОСТ Р ИСО 5725-2 и ГОСТ Р ИСО 5725-4) определения прецизионности и правильности методов и результатов измерений, приведенных в ГОСТ Р ИСО 5725-5;
е) изложить некоторые практические применения показателей правильности и прецизионности (ГОСТ Р ИСО 5725-6).
Представленные в виде таблицы рекомендации по применению основных положений ГОСТ Р ИСО 5725 в деятельности по метрологии, стандартизации, испытаниям, оценке компетентности испытательных лабораторий со ссылками на нормы государственных стандартов Российской Федерации, содержащих требования к выполнению соответствующих работ, приведены в приложении к предисловию в ГОСТ Р ИСО 5725-1.
Алгоритмы проведения экспериментов по оценке повторяемости, воспроизводимости, промежуточных показателей прецизионности, показателей правильности (характеристик систематической погрешности) методов и результатов измерений рекомендуется внедрять через программы экспериментальных метрологических исследований показателей точности (характеристик погрешности) результатов измерений, выполняемых по разрабатываемой МВИ, и (или) через программы контроля показателей точности применяемых МВИ.
ПРЕДИСЛОВИЕ К МЕЖДУНАРОДНОМУ СТАНДАРТУ ИСО 5725
Международный стандарт ИСО 5725-6 был подготовлен Техническим комитетом ИСО/ТК 69 «Применение статистических методов», Подкомитетом ПК 6 «Методы и результаты измерений».
ИСО 5725 состоит из следующих частей под общим заголовком «Точность (правильность и прецизионность) методов и результатов измерений»:
Часть 1. Основные положения и определения
Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений
Часть 3. Промежуточные показатели прецизионности стандартного метода измерений
Часть 4. Основные методы определения правильности стандартного метода измерений
Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений
Часть 6. Использование значений точности на практике
ИСО 5725 (части 1-6) в совокупности аннулирует и заменяет ИСО 5725:1986, область распространения которого была расширена включением правильности (в дополнение к прецизионности) и условий промежуточной прецизионности (в дополнение к условиям повторяемости и воспроизводимости).
ВВЕДЕНИЕ К МЕЖДУНАРОДНОМУ СТАНДАРТУ ИСО 5725
0.2 Необходимость рассмотрения «прецизионности» возникает из-за того, что измерения, выполняемые на предположительно идентичных материалах при предположительно идентичных обстоятельствах, не дают, как правило, идентичных результатов. Это объясняется неизбежными случайными погрешностями, присущими каждой измерительной процедуре; факторы, оказывающие влияние на результат измерения, не поддаются полному контролю. При практической интерпретации данных измерений эта изменчивость должна учитываться. Например, нельзя установить фактическое отклонение полученного результата измерений от некоторого определенного значения измеряемой величины, если он лежит в области неизбежных случайных погрешностей измерительной процедуры. Аналогичным образом, сопоставление результатов измерений измеряемых характеристик двух партий материала не выявит какого-либо существенного различия в качестве, если расхождение между результатами лежит в вышеупомянутой области.
0.3 В частях 1-5 ИСО 5725 обсуждаются подходы и приводятся методы оценки прецизионности (выраженной через стандартные отклонения повторяемости и воспроизводимости) и правильности (выраженной через различные составляющие систематической погрешности) измерений, выполняемых стандартным методом. Такая оценка, однако, была бы бесцельной, если бы ее результаты нельзя было использовать на практике.
0.4 Исходя из того, что точность метода измерений установлена, в настоящей части ИСО 5725 даны области применения значений точности на практике, например, в области продвижения коммерческих сделок или контроля показателей работы лабораторий и признания их технической компетентности.
Основы общей теории измерений
2.4. Точность и достоверность результата измерения
Применение рассмотренных выше элементов общей теории измерений необходимо для обеспечения точности и достоверности результата измерения. При многократных наблюдениях получают ряд значений, обрабатывая которые находят результат измерения. Для обработки применяют инструменты математической статистики, рассматривая ряд значений как выборку из генеральной совокупности. Опираясь на теорию вероятностей, математическая статистика позволяет оценить надежность и точность выводов, делаемых на основании ограниченного статистического материала.
Требуемая точность технических измерений может также обеспечиваться повторением многократных наблюдений. В этом случае многократные наблюдения одного и того же объекта выполняются несколько раз. Чтобы сократить время, необходимое для обработки нескольких рядов многократных наблюдений, в начале процесса обработки применяют индикаторы, позволяющие определить предпочтительный ряд и в дальнейшем обрабатывать только этот ряд.
Такими индикаторами является сумма остаточных погрешностей и сумма квадратов остаточных погрешностей. Эти индикаторы являются косвенной характеристикой несмещенности и эффективности оценки, полученной при обработке результатов многократных наблюдений.
Однако симметричность не является исчерпывающей характеристикой распределения. Следующим важным в метрологии признаком является компактность распределения. По этому признаку при фиксированном числе наблюдений предпочтительный ряд может быть определен индикатором эффективности. Эффективной называется та из нескольких возможных несмещенных оценок, которая имеет наименьшую дисперсию. Условию эффективности будет удовлетворять ряд с наименьшей суммой квадратов остаточных погрешностей.
Очевидно, что в практической метрологии эффективная оценка является предпочтительной. Признак эффективности свидетельствует о том, что субъективная составляющая случайной погрешности минимальна, наблюдения выполнялись более аккуратно и будет обеспечен наименьший размер случайной погрешности.
В теоретической метрологии рассматривается также состоятельная оценка, являющаяся идеальной моделью для многократных измерений, к которой желательно стремиться, но получить ее практически невозможно. При состоятельной оценке истинное и действительное значение совпадают, погрешность равна нулю. Это достигается бесконечным увеличением числа наблюдений. Состоятельной называется оценка, в которой при числе наблюдений, стремящемся к бесконечности, дисперсия стремится к нулю.
Задавая большую степень неопределенности контролируемым посредством измерений событиям, мы получаем большую уверенность в том, что они произойдут.
2.5. Прямые равноточные измерения с многократными наблюдениями
Метод прямых равноточных измерений с многократными наблюдениями является основополагающим, используется в технических измерениях для повышения достоверности результата, является основой для многих методов метрологических измерений, для методов косвенных измерений.
Равноточность измерений истолковывается в широком смысле, как одинаковая распределенность (в узком смысле равноточность измерений понимается как одинаковость меры точности всех результатов измерений). Наличие грубых ошибок (промахов) означает нарушение равноточности как в широком, так и в узком смысле.
Результат измерения находят как среднее арифметическое результатов наблюдений:
где 
Для оценки среднего квадратического отклонения результата измерения находим случайные отклонения результатов отдельных наблюдений, принимаем их за остаточные погрешности,
Для минимизации случайной и систематической составляющих погрешности, при наличии нескольких групп наблюдений (реализаций), используют два свойства остаточных погрешностей: сумма остаточных погрешностей равна нулю,
и сумма квадратов остаточных погрешностей минимальна,
Для дальнейших вычислений рекомендуется выбрать реализацию, удовлетворяющую этим условиям.
Степень рассеяния результатов наблюдений вокруг среднего арифметического значения характеризуется средним квадратическим отклонением, (СКО):
Оценка СКО учитывает ограниченность объем а выборки: при малом объем е выборки оценка СКО будет заметно больше, чем СКО, а при большом объем е выборки оценка СКО не будет заметно отличаться от СКО.
Полученное значение СКО результатов наблюдения не так универсально, как среднее арифметическое исправленных результатов наблюдений и не может быть непосредственно принято за значение случайной погрешности результата измерения. Для этого, прежде всего, необходимо восстановить размерность физической величины, ликвидировав нелинейность преобразования физической величины, разделив СКО результатов наблюдения на корень из 
Предположим, что наблюдения были получены в результате измерения цифровым вольтметром, имеющим класс точности, обозначенный цифрой 1,5 в кружочке, причем условия измерения выходили за нормальные пределы.
Основная инструментальная погрешность :
Дополнительная инструментальная погрешность :