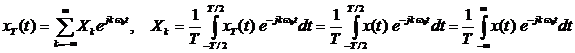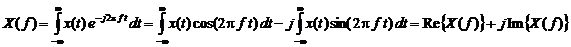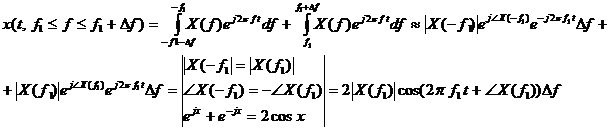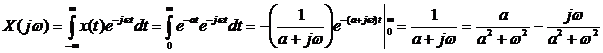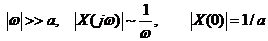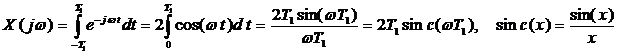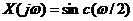чем отличаются спектры периодических и непериодических сигналов
Чем отличаются спектры периодических и непериодических сигналов
Частотные спектры периодических сигналов базируются на рядах Фурье.
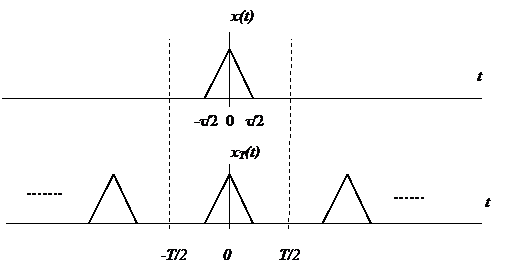
Пусть сигнал x ( t ) определен на интервале [- T /2, T /2]. Продолжим эту функцию
с периодом Т, при этом получим периодический сигнал xT ( t ). Графики:
 |
Представим периодический сигнал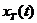 
в виде ряда Фурье (комплексная форма)
В теории сигналов и систем эти преобразования называют также непрерывно – временными преобразованиями Фурье, сокращенно НВПФ (англ. Continue Time Fourier Transform – CTFT ), поскольку они относятся к непрерывным во времени сигналам.
Связь между x ( t ) и X ( jω ) через преобразования Фурье может быть представлена в символической форме
Как и ряд Фурье, обратное преобразование Фурье дает сигнал x ( t ) в точках непрерывности и среднее значение в точках разрыва сигнала. В точках разрыва сходимость сопровождается явлением Гиббса.
В этих выражениях уже нет множителя 1/2π.
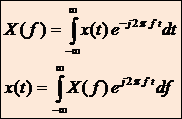
Какие сигналы x ( t ) имеют преобразование Фурье, т.е. для каких сигналов оно сходится? В математическом анализе доказывается, что сигналы должны
Амплитудный и фазовый спектры непериодического сигнала
Обратимся к выражению обратного преобразования Фурье и запишем его приближенно
В общем случае X ( f ) является комплексной функцией действительного аргумента f (частоты), т.к. 
Её можно представить в виде модуля и аргумента (фазы)
Выражение спектральной плотности с помощью формулы Эйлера можно записать в виде
Следовательно, достаточно вычислять спектры только для положительных частот.
В связи с симметрией обычно изображают спектры только для положительных частот.
Выразим вклад диапазона частот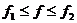 
в сигнал x ( t )
Отсюда вклад элементарного диапазона частот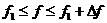 
в сигнал x ( t )
Фаза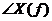 
выражает угловой (временной) сдвиг гармоники на частоте f при t = 0.
Сигналы, спектр которых (полоса частот) включает начало координат (нулевую частоту), называют низкочастотными. Узкополосным (полосовым) называют сигнал, спектр которого концентрируется около некоторой частоты, удаленной от начала координат. Сигналы реального мира в большинстве случаев являются низкочастотными, узкополосные сигналы используются в системах связи.
Примеры определения спектров
Для 
2. Прямоугольный импульс, длительность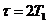 
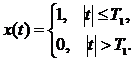
Преобразование Фурье (комплексный спектр)
если длительность импульса 2 T 1 ® 0, то ω1 ® ∞, т.е. чем уже импульс, тем шире спектр.
имеет постоянный (бесконечно широкий) спектр при любой частоте ω.
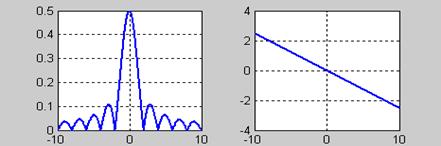
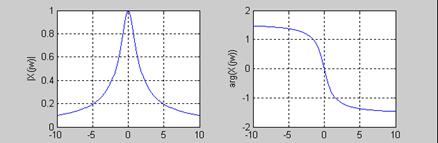
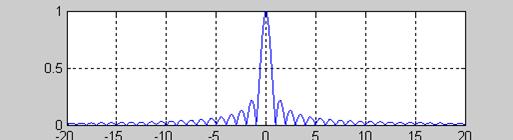
Графики амплитудного и фазового спектров
У смещенной δ – функции – линейный фазовый спектр
Теорема Парсеваля для непериодических сигналов
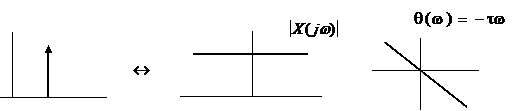
Энергия непериодического сигнала
Выразим сигнал через преобразование Фурье, тогда
Функция 
имеет смысл спектральной плотности энергии или энергетического спектра сигнала x ( t ). Она характеризует распределение энергии сигнала по частоте. Поскольку амплитудный спектр – четная функция частоты, то можно интегрировать по положительным значениям частоты, удвоив значение интеграла, т.е.
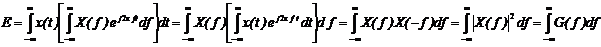
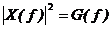
Связь спектров непериодического и периодического сигналов
Найдем связь между спектром непериодического сигнала и периодической последовательности с периодом Т таких сигналов. Для этого сравним выражения прямого преобразования Фурье и коэффициентов комплексной формы ряда Фурье
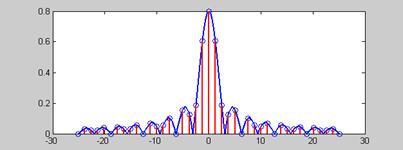
Следовательно, совокупность точек TXk дискретного спектра периодического сигнала лежит на кривой сплошного спектра непериодического сигнала. Графическое пояснение
Здесь период прямоугольной волны Т = 5, длительность импульса τ =2, амплитуда U = 1.
При увеличении периода Т спектр становится более частым.
1. Для непериодических сигналов непрерывного времени спектральный анализ основан на выражениях преобразования Фурье (НВПФ)
Нотация: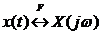 
2. Спектральная функция сигнала X ( jω ) имеет смысл плотности комплексных (имеющих модуль и фазу) амплитуд гармоник, приходящихся на единичный интервал частот вблизи рассматриваемой частоты ω.
Понятие о спектре периодических и непериодических сигналов
Среди разнообразных систем ортогональных функций, которые могут использоваться в качестве базисов для представления сигналов, исключительное место занимают гармонические (синусоидальные и косинусоидальные) функции. Значение гармонических сигналов обусловлено рядом причин:
I.Гармонические сигналы инварианты относительно преобразований, осуществляемых стационарными линейными электрическими цепями. Если такая цепь возбуждена источником гармонических колебаний, то сигнал на выходе цепи остаётся гармоническим с той же частотой, отличаясь от входного сигнала лишь амплитудой и начальной фазой.
II.Техника генерирования гармонических сигналов относительна проста. Будем использовать гармонические сигналы в качестве ортонормированного базиса.
Если какой-либо сигнал представлен в виде суммы гармонических колебаний с различными частотами, т.е. разложен по частоте, то говорят, что осуществлено спектральное разложение сигнала.
Совокупность значений амплитуд и фаз гармонических компонент на различных частотах называется спектром сигнала.
2.2 Спектральное представление периодических сигналов
Математической моделью процесса, повторяющегося во времени, является периодический сигнал 
со следующим свойством:
, 
, (2.1)
где Т- период сигнала.
Найдём спектральное разложение такого сигнала.
В соответствии с формулой (1.10) получим спектральное разложение:
(2.2)
справедливое на всей бесконечности оси времени.
Ряд вида (2.2) называется рядом Фурье данного сигнала.
Введём понятия основной частоты 
последовательности, образующей периодический сигнал. Примем интервал разложения от 
до 
. Вычисляя коэффициенты разложения по формуле (1.12) запишем ряд Фурье для периодического сигнала:
(2.3)
(2.4)
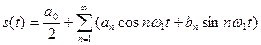
В общем случае периодический сигнал содержит не зависящую от времени постоянную составляющую и бесконечный набор гармонических колебаний, так называемых гармоник с частотами 
кратными основной частоте последовательности.
Каждую гармонику можно описать её амплитудой 
и начальной фазой 
. Для этого коэффициенты ряда Фурье записывают в виде:
, 
,
Подставив эти выражения в (2.3), получим другую, эквивалентную форму ряда Фурье:
(2.5)
которая иногда оказывается удобнее.
Изобразим коэффициенты ряда Фурье графически. Такое изображение называется спектральной диаграммой сигнала.
Спектры периодических сигналов являются дискретными. Спектральное разложение можно выполнить также, используя систему базисных функций, состоящую из экспонент с мнимыми показателями:
(2.6)
Функции этой системы периодичны с периодом Т и ортонормированны на отрезке времени 
.
Тогда мы получим показательную форму записи ряда Фурье:
(2.7)
(2.8)
Выражение (2.7) представляет собой ряд Фурье в комплексной форме.
Спектр сигнала в соответствии с формулой (2.8) содержит компоненты на отрицательной полуоси частот, причём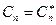 
. Слагаемые в ряде (2.7) с положительными и отрицательными частотами объединяются в пары.
Отрицательная частота – понятие не физическое, а математическое, вытекающее из способа представления комплексных чисел.