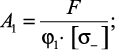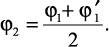чем определяется устойчивость сжатых элементов
Научная электронная библиотека
Лекция 12. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ
Понятие об устойчивости и критической силе. Проектировочный и проверочный расчеты.
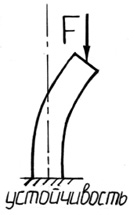
В конструкциях и сооружениях большое применение находят детали, являющиеся относительно длинными и тонкими стержнями, у которых один или два размера поперечного сечения малы по сравнению с длиной стержня. Поведение таких стержней под действием осевой сжимающей нагрузки оказывается принципиально иным, чем при сжатии коротких стержней: при достижении сжимающей силой F некоторой критической величины, равной Fкр, прямолинейная форма равновесия длинного стержня оказывается неустойчивой, и при превышении Fкр стержень начинает интенсильно искривляется (выпучивается). При этом новым (моментным) равновесным состоянием упругого длинного становится некоторая новая уже криволинейная форма. Это явление носит название потери устойчивости.
Рис. 37. Потеря устойчивости
Устойчивость – способность тела сохранять положение или форму равновесия при внешних воздействиях.
Критическая сила (Fкр) – нагрузка, превышение которой вызывает потерю устойчивости первоначальной формы (положения) тела. Условие устойчивости:
Устойчивость сжатого стержня. Задача Эйлера.
При определении критической силы, вызывающей потерю устойчивости сжатого стержня, предполагается, что стержень идеально прямой и сила F приложена строго центрально. Задачу о критической нагрузке сжатого стержня с учетом возможности существования двух форм равновесия при одном и том же значении силы решил Л. Эйлер в 1744 году.
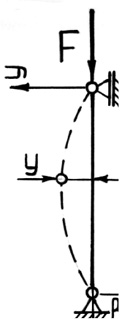
Рис. 38. Сжатый стержень
Рассмотрим шарнирно опертый по концам стержень, сжатый продольной силой F. Положим, что по какой-то причине стержень получил малое искривление оси, вследствие чего в нем появился изгибающий момент M:
где y – прогиб стержня в произвольном сечении с координатой x.
Для определения критической силы можно воспользоваться приближенным дифференциальным уравнением упругой линии:
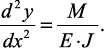
Проведя преобразования, можно увидеть, что минимальное значение критическая сила примет при n = 1 (на длине стержня укладывается одна полуволна синусоиды) и J = Jmin (стержень искривляется относительно оси с наименьшим моментом инерции)
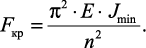
Это выражение – формула Эйлера.
Зависимость критической силы от условий закрепления стержня.
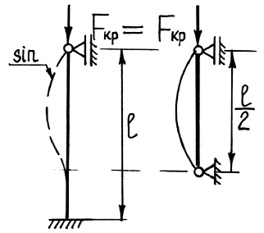
Формула Эйлера была получена для, так называемого, основного случая – в предположении шарнирного опирания стержня по концам. На практике встречаются и другие случаи закрепления стержня. При этом можно получить формулу для определения критической силы для каждого из этих случаев, решая, как в предыдущем параграфе, дифференциальное уравнение изогнутой оси балки с соответствующими граничными условиями. Но можно использовать и более простой прием, если вспомнить, что, при потере устойчивости на длине стержня должна укладываться одна полуволна синусоиды.
Рассмотрим некоторые характерные случаи закрепления стержня по концам и получим общую формулу для различных видов закрепления.
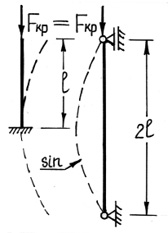
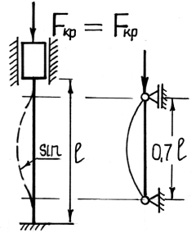
Рис. 39. Различные случаи закрепления стержня
Общая формула Эйлера:
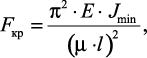
где μ·l = lпр – приведенная длина стержня; l – фактическая длина стержня; μ – коэффициент приведенной длины, показывающий во сколько раз необходимо изменить длину стержня, чтобы критическая сила для этого стержня стала равна критической силе для шарнирно опертой балки. (Другая интерпретация коэффициента приведенной длины: μ показывает, на какой части длины стержня для данного вида закрепления укладывается одна полуволна синусоиды при потере устойчивости.)
Таким образом, окончательно условие устойчивости примет вид
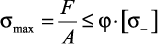
Рассмотрим два вида расчета на устойчивость сжатых стержней – проверочный и проектировочный.
Проверочный расчет
Порядок проверочного расчета на устойчивость выглядит так:
– исходя из известных размеров и формы поперечного сечения и условий закрепления стержня, вычисляем гибкость;
– по справочной таблице находим коэффициент понижения допускаемого напряжения, затем определяем допускаемое напряжение на устойчивость;
– сравниваем максимальное напряжение с допускаемым напряжением на устойчивость.
Проектировочный расчет
При проектировочном расчете (подобрать сечение под заданную нагрузку) в расчетной формуле имеются две неизвестные величины – искомая площадь поперечного сечения A и неизвестный коэффициент φ (так как φ зависит от гибкости стержня, а значит и от неизвестной площади A). Поэтому при подборе сечения обычно приходится пользоваться методом последовательных приближений:
– обычно в первой попытке принимают φ1 = 0,5…0,6 и определяют площадь сечения в первом приближении
– по найденной площади A1 подбирают сечение и вычисляют гибкость стержня в первом приближении λ1. Зная λ, находят новое значение φ′1;
– далее, используя найденный φ′1, проверяют условие устойчивости, и если σmaxmax и [σу] значительно отличаются друг от друга (более чем на 5 %), следует повторить расчет, приняв во второй попытке
Выбор материала и рациональной формы сечения.
Выбор материала. Так как в формулу Эйлера из всех механических характеристик входит лишь модуль Юнга, то для повышения устойчивости стержней большой гибкости нецелесообразно применять высокопрочные материалы, так как модуль Юнга для всех марок сталей примерно одинаков.
Для стержней малой гибкости применение высокосортных сталей оправдано, так как с повышением предела текучести у таких сталей повышаются и критические напряжения, а значит и запас устойчивости.
Форма сечения. При проектировании стержней, работающих на устойчивость, следует выбирать такую форму сечения, чтобы гибкость стержня была одинаковой относительно обеих главных осей его сечения (условие равноустойчивости), а значит максимальный и минимальный моменты инерции такого сечения должны быть одинаковы Jmax = Jmin.
Кроме того, необходимо стремиться к получению при данной площади наибольших радиусов инерции. Для этого необходимо выбирать сечения, большая часть площади которых по возможности была удалена от центра тяжести (трубчатые, коробчатые сечения).
По степени рациональности известные сечения можно распределить следующим образом: трубчатое сечение, коробчатое, двутавровое, состоящее из швеллеров, квадратное, круглое, прямоугольное.
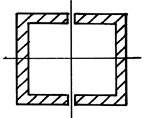
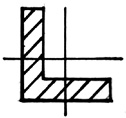
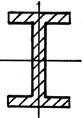
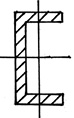
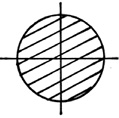
Рис. 40. Поперечные сечения, распределенные по степени рациональности
Устойчивость стержней
По этой ссылке вы найдёте полный курс лекций по математике:
Устойчивость сжатых стержней Общие понятия Формула Эйлера для определения критической силы сжатого стержня Влияние условия закрепления стержня на величину критической силы Пределы применимости формулы Эйлера Практический способ расчета сжатых стержней на устойчивость Выбор рациональной формы поперечного сечения сжатого стержня.
Примеры расчетов на устойчивость Библиографический список Устойчивость сжатых стержней Общие понятия При расчёте на прочность элементов конструкций предполагается, что при их деформации имеет место заранее известная форма равновесия. Однако это возможно лишь при определенной величине внешних нагрузок. В зависимости от внешних сил деформированный стержень может находиться в устойчивом или неустойчивом состоянии равновесия.
Упругое равновесие будет устойчивым, если деформированный стержень при любом малом отклонении от состояния равновесия стремится возвратиться и возвращается к первоначальному состоянию после удаления внешнего воздействия Упругое равновесие будет неустойчивым, если деформированный стержень, выведенный из состояния равновесия каким-либо внешним воздействием, после удаления внешнего воздействия в исходное состояние не возвращается (рис 1.1, б).
Между этими двумя состояниями равновесия существует переходное состояние, при котором деформированный стержень находится в безразличном равновесии: он может сохранить первоначально приданную ему форму, но может и потерять её от самого незначительного воздействия. Это состояние безразличного равновесия называют критическим (рис. 1.1, в).
При потере устойчивости происходит переход к некоторому новому положению равновесия, причём переход сопровождается, как правило, большими перемещениями, возможным возникновением остаточных деформаций, а в отдельных случаях выходом конструкции из строя. Наиболее простым примером является потеря устойчивости центрально сжатого стержня (рис. 1.2, а). Тонкостенная труба, нагруженная внешним давлением, при превышении определённой величины его также теряет устойчивость (рис. 1.2, б.). Потеря устойчивости может происходить и при изгибе, например, тонкой полосы (рис. 1.2, в).
Из всего многообразия расчётов на устойчивость упругих систем подробно рассмотрим лишь случай потери устойчивости центрально сжатого стержня. Наименьшее значение центрально приложенной сжимающей силы, при которой прямолинейная форма равновесия стержня становится криволинейной, называют критической силой. До момента наступления критического состояния центрально сжатого стержня упругие деформации растут весьма незначительно, почти незаметно для глаза.
Но с момента наступления критического состояния, деформации нарастают крайне быстро и практически нет времени для принятия мер по предотвращению грозящей катастрофы. Поэтому при расчёте на устойчивость критическая нагрузка подобна разрушающей при расчёте на прочность. Конструкция должна удовлетворять не только требованиям прочности и жёсткости, но и требованиям устойчивости. В целях безопасности допускаемая нагрузка, естественно, должна быть меньше критической, т.е. условие устойчивости запишется где – допускаемая нагрузка; – критическая сила; – коэффициент запаса устойчивости.
Для стальных стоек nу = 1,8-3,0, причём меньшее значение устанавливаются для стержней с большей гибкостью; для чугунных стоек nу=5,0-5,5; для деревянных Явление потери устойчивости центрально cжатого стержня называют продольным изгибом. 1.2. Формула Эйлера для определения критической силы сжатого стержня Рассмотрим сжатый стержень с шарнирно закреплёнными концами в критическом состоянии, т.е. когда сжимающая сила достигла своего критического значения.
При этом примем, что стержень находится в слегка изогнутом состоянии. Если моменты инерции относительно двух главных центральных осей (Z, У) поперечного сечения не равны между собой, то изогнутая ось стержня находится в плоскости оси наименьшей жёсткости. Изобразим искривлённую ось стержня в прямоугольной системе координат z, у Предположим, что критическая сила не вызывает в стержне напряжений, превышающих предел пропорциональности, и что рассматриваются только малые отклонения оси стержня от прямолинейной формы.
Практически, кроме первой формы (n=1) потери устойчивости сжатого стержня осуществить остальные трудно, так как при увеличении силы Р выше критического значения, соответствующего первой форме, возникнут большие остаточные деформации или даже произойдёт разрушения стержня. Поэтому критическая сила, соответствующая n=1, считается как опасная (разрушающая). Считая, что n=1, а из формулы (1.3) получим (1.8) Формула (1.8) называется формулой Эйлера. 1.3.
Возможно вам будут полезны данные страницы:
Влияние условий закрепления концов стержня на величину критической силы При выводе формулы Эйлера было показано, что в случае достижения внешней силой критического значения, изогнутая ось стержня описывает полуволну синусоиды. Это легко осуществляется при шарнирном закреплении его концов. При других способах закрепления количество полуволн изменяется.
Поэтому для общего способа опорных закреплений стержня формулу Эйлера запишем в следующем виде: – приведённая длина, на которой укладывается одна полуволна; – коэффициент приведения длины, зависит от закрепления концов стержня. Величина коэффициента μ для некоторых распространённых закреплений концов сжатого стержня приведена на рис. 1.4. 1.4.
Пределы применимости формулы Эйлера Вывод формулы Эйлера выполняется на основе дифференциального уравнения упругой оси в предположении, что деформации подчиняются закону Гука. Следовательно, напряжения, соответствующие критической силе, должны быть меньше или равны пределу пропорциональности: (1.10) Критическое напряжение с учётом выражения (1.9) запишется так: где – минимальный радиус инерции сечения, (1.12) Под λ понимаем гибкость стержня.
10 Из формулы (1.11) следует, что критическое напряжение зависит от свойств материала (модуль упругости Е) и геометрических характеристик сечения, выраженных через гибкость стержня. Пределы применимости формулы (1.11) можно выразить через гибкость стержня. Тогда уравнение (1.12) запишется так: Отсюда определяем продольную гибкость С учётом этого, условие применимости формулы Эйлера можно записать так: В этом случае критические напряжения будут меньше предела пропорциональности.
В качестве примера определим предельное значение гибкости предел пропорциональности, Если для стержней фактическая гибкость то для расчёта на устойчивость формула Эйлера непригодна, так как критическое напряжение σкр будет больше предела пропорциональности σпц. Ф.С. Ясинский на основе обработки результатов экспериментов по продольному изгибу стержней за пределом упругости предложил формулу для вычисления критического напряжения где λ – гибкость стержня; а, в и с – размерные опытные коэффициенты, величина которых различна для разных материалов, например:
для Ст. 3 – λпр=100; а=310 МПа; в=1,14 МПа; с=0; для Ст. 5 – λпр=85; а=467 МПа; в=3,62 МПа; с=0; для чугуна для сосны – λпр=110; а=293 МПа; в=0,194 МПа; с=0. Изменение величины критического напряжения в зависимости от значения гибкости стержня можно показать графически. На рис. 1.5 эта зависимость показана для Ст. 3. Для участка правее точки А гибкость стержня λ > λпр, т. е. в этом случае справедлива формула Эйлера (1.12), а критические напряжения σкр меньше предела пропорциональности σпц.
Стержни, для которых справедлива формула Эйлера, называют стержнями большой гибкости, и они испытывают только упругие деформации. Ввиду того что стержни с чрезмерно большой гибкостью воспринимают малые нагрузки, на практике гибкость ограничивают величиной λ = 200. Для участка диаграммы, расположенного левее точки А, при гибкости стержней λ > λпр критические напряжения σкр больше предела пропорциональности σпц, и здесь формула Эйлера несправедлива, так как даёт завышенные результаты расчета критических напряжений. На этом участке используют формулу Ясинского (1.13) при с=0, это изображается на диаграмме прямой линией АВ.
Точка В здесь соответствует пределу текучести σт или гибкости λ = 40.
Стержни, у которых гибкость находится в пределах (40 ≤ λ ≤ 100), т.е. для которых справедлива формула Ясинского, называют стержнями средней гибкости. Они испытывают упруго-пластичные деформации. На участке диаграммы левее точки В возникают только пластические деформации, и расчёт стержня на устойчивость не производится, так как их разрушение происходит раньше, чем возникает потеря устойчивости. Стержни с гибкостью до 40 называют стержнями малой гибкости. 1.5.
Практический способ расчёта сжатых стержней на устойчивость 12 Сжатые стержни кроме проверки на прочность должны быть проверены на устойчивость (рис. 1.6). Условие прочности имеет вид: Условие устойчивости: Здесь А – площадь поперечного сечения стержня без учёта ослаблений отверстиями, пазами и т.п.; АН – площадь сечения с учётом ослаблений, – допускаемое напряжение на устойчивость; nу – коэффициент запаса на устойчивость. Величину коэффициента запаса nу принимают несколько больше основного коэффициента запаса на прочность.
Это делается потому, что для центрально сжатых стержней ряд обстоятельств, неизбежных на практике (эксцентриситет приложения сжимающих сил, начальная кривизна и неоднородность стержня), способствует продольному изгибу. При других видах деформаций эти факторы влияют значительно меньше, не вызывая заметного роста напряжений и перемещений. Допускаемые напряжения на устойчивость [σу] и допускаемое напряжения на прочность при сжатии [σ] взаимно связаны соотношением где φ – коэффициент уменьшения основного допускаемого значения. Этот коэффициент для разных материалов в зависимости от гибкости стержня можно определить в П. 6. Условие устойчивости сжатого стержня будет удовлетворять, если 13 (1.17)
В практике расчёт сжатых стержней на устойчивость может быть двух видов: проверочный и проектировочный. При проверке устойчивости в зависимости от заданных размеров поперечного сечения стержня, его длины и вида опорных закреплений, а также заданной сжимающей силы находят величину действительного напряжения и сравнивают ее с допускаемой. В некоторых случаях находят допускаемую и критическую силу, а также коэффициент запаса. В проектировочных расчётах определяют размеры поперечного сечения сжатого стержня по заданной величине сжимающей силы, длине и виду концевых закреплений.
Если он отличается от заданного более чем на 3%, то расчёт повторяют, причём для второго этапа принимают φ2(зад) = 0,5(φ1 + φ1Т). После окончательно принятых размеров сечения выполняют проверку на прочность при наличии ослаблений, используя условия прочности: Расхождение не должно превышать ± 5 %. 1.6. Выбор рациональной формы поперечного сечения сжатого стержня С точки зрения экономии материала наиболее рациональной формой поперечного сечения сжатого стержня будет такая, при которой величина наименьшего радиуса инерции imin при одной и той же площади является 14 наибольшей.
К таким сечениям относят круглые, кольцевые, квадратные и т.д. Прокатные профили, как двутавры, швеллеры, уголки, не являются рациональными с этой точки зрения. Однако из них можно скомпоновать сечение, отвечающее этому требованию, как показано рис. 1.7. 1.7. Примеры расчётов на устойчивость Пример 1.1 Для заданных стержней (рис. 1.8) найти значения критической сила Ркр, допускаемой силы [Р] и коэффициента запаса устойчивости nу. Стержни изготовлены из малоуглеродистой стали с механическими характеристиками σт = 240 МПа, [σ] = 160 МПа.
Длина стержней l = 0,85 м, сечение прямоугольное размерами вхh = 60х40 мм. Способы закрепления концов и соответствующие коэффициенты приведения μ показаны на рис. 1.8. 1. Геометрические характеристики сечения: площадь поперечного сечения минимальный осевой момент инерции минимальный радиус инерции сечения 2. Гибкость стержней определяем по формуле 3. Находим значения критического напряжения: 4. Значение критической силы найдём по формуле 5.
| Допускаемую величину сжимающей |
силы находим в соответствии с (1.17) из выражения где коэффициент понижения допускаемого напряжения находим по табл. 1.1 с использованием линейной интерполяции: Аналогично находим при λ=147,8 φ=0,329. Величина допускаемой силы: 6. Коэффициент запаса устойчивости: Стержень из малоуглеродистой стали с механической характеристикой [σ]т = 160 МПа, жёстко защемлён и нагружен сжимающей силой Р=300 кН. Длина стержня l = 2,8 м (рис. 1.9).
Подобрать из условия рвноустойчивости размеры сечения в форме двух швеллеров. Решение 1. В первом приближении задаёмся φ1 = 0,6. 2. Требуемую площадь поперечного сечения находим по формуле (1.9): 3. Выбираем по сортаменту сечение в форме двух швеллеров №14У, площадь которого сечения Момент инерции Из условия равноустойчивости считаем Радиус инерции 4. Гибкость стержня 5. По табл. 9.1 находим при λ=99,8 φ1табл = 0,618. 6. Во втором приближении принимаем 7.
Требуемая площадь сечения 8. Из сортамента выбираем два швеллера №14У с геометрическими характеристиками 9. Гибкость стержня 10. По табл. 1.1 находим φ2табл = 0,618 – значение отличается от заданного на величину что допускается. 11. Из условия равноустойчивости – момент инерции швеллера относительно оси У; в – расстояние между осями Тогда, решая равенство 12. Ширина сечения В составит где z0 – координата центра тяжести швеллера Таблица 1. Коэффициенты φ Гибкость Значение φ для стали марок 4, 3, 2, ОС стали марки чугуна дерева
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Глава 9. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ
Под действием сжимающей силы стержень может утратить первоначальную форму равновесия и искривиться. Произойдет потеря устойчивости стержня. Наименьшая сила, при которой происходит потеря устойчивости, называется критической и определяется по формуле Эйлера:
где Е – модуль упругости материала стержня;
Imin– минимальный осевой момент инерции сечения стержня;
μ – коэффициент приведения длины, зависящий от способа закрепления концов стержня (рис. 38);
l – длина стержня, μ ∙ l = lпр – приведенная длина стержня.
Рис. 38. Значения коэффициента μ приведенной длины и критической
силы Fкр для сжатых стержней при различных способах закрепления концов
Напряжения, вызванные критической силой, называются критическими и определяются по формуле Эйлера:

где λ – гибкость стержня, 

А – площадь поперечного сечения стержня.
Формула Эйлера применима при условии, что критическое напряжение не превышает предела пропорциональности материала 
где 
Формулой Эйлера можно пользоваться, если гибкость стержня 

При значениях гибкости от 0 до 40 

При значениях гибкости, лежащих в интервале 

где а, b, с – коэффициенты, зависящие от материала и имеющие размерность напряжения. Они приведены в табл. 12.
Опытные коэффициенты для определения 
| Материал | а | b | с |
| Сталь Ст3 Сталь Ст5 Чугун Сосна (сжатие вдоль волокон) | 29,3 | 1,14 3,62 0,194 | 0,053 |
Критическая сила является недопустимой для сжатых стержней.
Определение допускаемой сжимающей силы [F] производят двумя способами. Первый способ используется, когда для рассчитываемого стержня известны длина, способ закрепления концов, форма и размеры поперечного сечения, материал, коэффициент запаса на устойчивость. Вначале определяют критическую силу Fкр = sкр ∙ А, а затем допускаемую силу [F]:
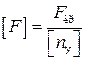
где [nу] – допускаемый коэффициент запаса на устойчивость.
Значения допускаемых коэффициентов запаса на устойчивость [nу] для различных материалов приведены в табл. 13.
Допускаемые коэффициенты запаса на устойчивость
для различных материалов
| Материал | [ny] |
| Сталь Ст 3 | 1,8  3 3 |
| Сталь Ст 5 | 1,8  3 3 |
| Чугун | 5  5,5 5,5 |
| Сосна (сжатие вдоль волокон) | 2,8  3,2 3,2 |
Второй способ основан на применении таблиц j (l). Сначала определяют гибкость стержня λ, затем по таблице находят j (l) и вычисляют [F] по формуле
где j – коэффициент уменьшения допускаемого напряжения при сжатии [sс].
Значения коэффициента j в зависимости от гибкости λ и материала стержня приведены в табл. 14.
Для расчета критического напряжения, критической силы, допускаемой сжимающей силы и коэффициента запаса на устойчивость
можно использовать блок-схему, представленную на рис. 39.
Значение коэффициента продольного изгиба j (l)
для различных материалов
| Гибкость λ | Значение j (l) | ||
| Сталь Ст3, Ст4 | Сталь Ст5 | Чугун | Дерево |
| 1,00 | 1,00 | 1,00 | 1,00 |
| 0,99 | 0,98 | 0,97 | 0,99 |
| 0,97 | 0,96 | 0,91 | 0,97 |
| 0,95 | 0,93 | 0,81 | 0,93 |
| 0,92 | 0,89 | 0,69 | 0,87 |
| 0,89 | 0,85 | 0,57 | 0,80 |
| 0,86 | 0,80 | 0,44 | 0,71 |
| 0,81 | 0,74 | 0,34 | 0,60 |
| 0,75 | 0,67 | 0,26 | 0,48 |
| 0,69 | 0,59 | 0,20 | 0,38 |
| 0,60 | 0,50 | 0,16 | 0,31 |
| 0,52 | 0,43 | – | 0,25 |
| 0,45 | 0,37 | – | 0,22 |
| 0,40 | 0,32 | – | 0,18 |
| 0,36 | 0,28 | – | 0,16 |
| 0,32 | 0,25 | – | 0,14 |
| 0,29 | 0,23 | – | 0,12 |
| 0,26 | 0,21 | – | 0,11 |
| 0,23 | 0,19 | – | 0,10 |
| 0,21 | 0,17 | – | 0,09 |
| 0,19 | 0,15 | – | 0,08 |
| 0,17 | 0,14 | – | – |
| 0,16 | 0,13 | – | – |
Практически расчет на устойчивость ведется с использованием коэффициента j – коэффициента уменьшения допускаемого напряжения при сжатии [sс].
Условие устойчивости имеет вид
Расчет на устойчивость сводится к недопущению потери устойчивости, т.е. искривления стержня.
Подбор поперечного сечения стержня при заданных длине, сжимающей силе и материале выполняется с использованием таблиц значений j (l) методом последовательных приближений в следующем порядке.
1. Задают произвольное значение j. Например, полагают j = 0,5.
2. Вычисляют допускаемое напряжение на устойчивость:
3. Определяют площадь поперечного сечения из условия
4. Подбирают размеры сечения или номер профиля. Вычисляют
площадь А, минимальный момент инерции Imin, минимальный радиус инерции imin поперечного сечения.
5. Определяют гибкость стержня l.
6. Если гибкость стержня l > 220, то считают, что заданная сила
F равна допускаемой [F]:
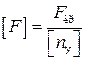
где Fкр – критическая сила (определяется по формуле Эйлера), а nу – коэффициент запаса на устойчивость (выбирается по табл. 13).
Тогда можно определить значение наименьшего момента инерции Imin по формуле

7. Если гибкость стержня l 
8. Вычисляют действующее напряжение s = 
9. Вычисляют допускаемое напряжение [sу] = j и ∙[sс].
10. Сравнивают действующее напряжение с допускаемым, вычисляя относительную разницу k: k = 
11. Если k > 0, то имеем недонапряжение, если k 5%, то в качестве второго приближения берут
j2 = j + j и и повторяют расчет, пока не будет выполняться условие |k| £ 5%.
Подбор сечения по изложенному алгоритму представлен в виде
В сопротивлении стержней продольному изгибу основную роль
играет гибкость стержня и, следовательно, величина наименьшего радиуса инерции сечения, поэтому существенным является вопрос не только величины площади сечения, как при расчете на прочность, но и формы поперечного сечения.
Для наиболее оптимального выбора сечения необходимо
конструировать сечение так, чтобы при определенной площади
величина наименьшего радиуса инерции была бы возможно большей. Для этого прежде всего следует стремиться к тому, чтобы центральные моменты инерции сечения были равны. Такой стержень будет оказывать одинаковое сопротивление потере устойчивости в любом направлении.
Далее, необходимо стремиться к получению при данной площади
наибольших центральных моментов инерции. Для этого надо разместить материал сечения по возможности дальше от центра тяжести. Этим условиям хорошо удовлетворяют трубчатое сечение или сечение, составленное из двух швеллеров, раздвинутых на определенное расстояние.
На выбор материала для сжатых стержней влияют два фактора:
Дата добавления: 2014-11-13 ; просмотров: 134 ; Нарушение авторских прав