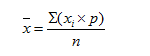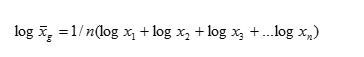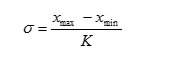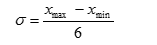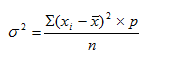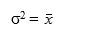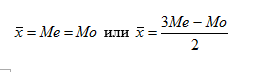чем определяется однородность вариационного ряда

Вариационные ряды — помощь в оценке распределения явлений по величине признаков

Вариационный ряд (frequency table)- ранжированный ряд распределения по величине какого-либо признака. Этот признак носит название варьирующего, а его отдельные числовые значения называются вариантами и обозначаются через «х». Число, показывающее, сколько раз данная варианта встречается в вариационном ряду, называется частотой и обозначается через «р».

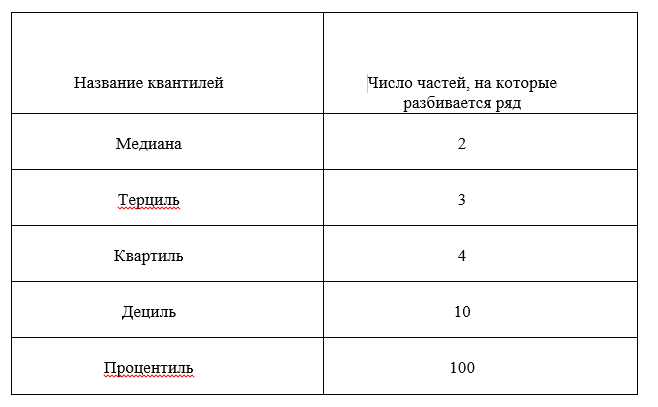
Вариационный ряд можно разбивать на отдельные (по возможности равные) части, которые называются квантилями (quantile). Наиболее часто употребляемые квантили представлены в таблице:

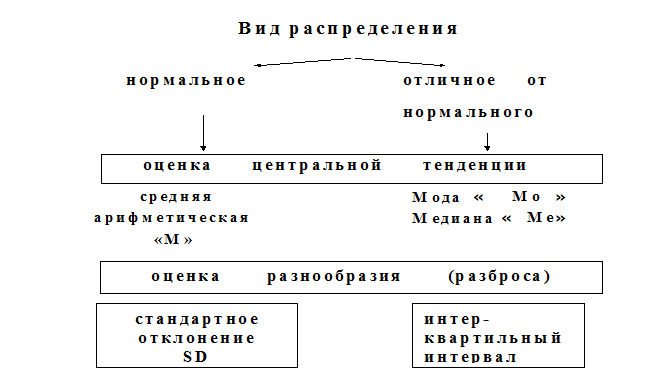
Рис. 1 Этапы описания (обобщения) количественного признака

Виды вариационных рядов

Вариационные ряды могут быть следующих видов:

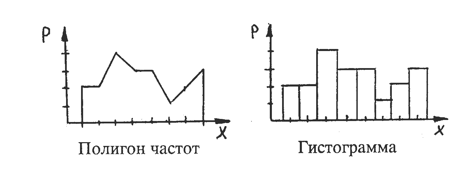
Графическое изображение вариационных рядов

где х — варианты, р — частоты.

Основные характеристики вариационного ряда

Такие характеристики зависят от оцениваемых показателей:

1). Показатели, характеризующие центральную тенденцию (central tendency) или уровень ряда: средние величины или меры расположения (собственно средние и структурные средние).

2). Показатели, характеризующие разнообразие (рассеяние, вариацию, разброс) (spread) признака: стандартное отклонение, дисперсия, размах, интерквартильный интервал.

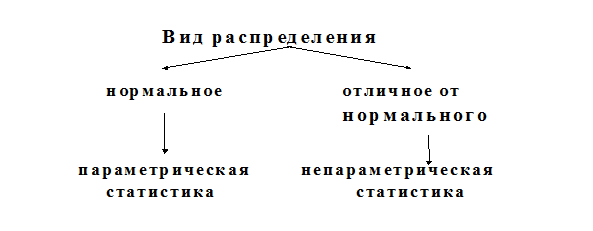
Выбор характеристик центральной тенденции и разнообразия признака прежде всего зависит от вида распределения. В случае нормального распределения используют показатели параметрической статистики, в случае распределения, отличного от нормального и при неизвестном виде распределения применяют показатели непараметрической статистики.

Средние величины

Средняя величина — обобщающий коэффициент, который характеризует наиболее типичный размер определенного признака в целом для совокупно­сти или для отдельных ее частей. Расчет средних величин имеет смысл только для качественно однородной совокупности, в связи с этим в одной совокупности может быть столько средних, на сколько однородных групп она может быть разбита.

Виды средних величин

Средняя арифметическая(mean) — применяется, если варианты возрастают (убывают) в арифметической прогрессии.

х — средняя арифметическая;

р — частота встречаемости варианты;

n — число наблюдений

Свойства средней арифметической:

— носит обобщающий характер;

— имеет абстрактное значение;

— алгебраическая сумма отклонений отдельных вариант от средней равна 0 (сущность средней и способ проверки правильности расчета средней);

— сумма квадратов отклонений отдельных вариант от средней меньше суммы квадратов отклонений вариант от любой другой величины, неравной средней;

— сумма произведений отдельных вариант на свои частоты равна произведению средней на число наблюдений (единство суммарного действия и способ провер­ки правильности расчета средней);

— если частоту всех вариант пропорционально изменить, то средняя арифметическая от этого не изменится.

Средняя геометрическая — вычисляется, если варианты возрастают (убыва­ют) в геометрической прогрессии.

На практике используют логарифмированную формулу:

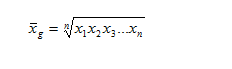
Структурные средние

Мода (Мо) (mode)- наиболее часто встречающаяся в вариационном ряду варианта.

Медиана (Me)(median) — варианта, которая делит вариационный ряд на две равные

части. Медиана используется:

Характеристики разнообразия вариационного ряда

— приблизительный расчет стандартного отклонения по амплитуде:

где К — коэффициент Ермолаева, рассчитывается по специальной таблице с учетом числа наблюдений (см. приложение).

При числе наблюдений больше 30:

Стандартное отклонение наиболее часто используется при определении нормы и патологии, в основе которого лежит «правило трех сигм», справедливое только для нормального распределения.

Сводная таблица формул

для нахождения средних значений и мер рассеяния

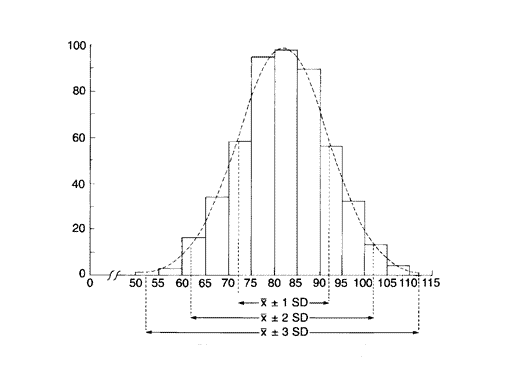
«Правило трех сигм»

68.3 % всех вариант отклоняются от своей средней не более, чем на s

95.4% вариант находятся в пределах X ± 2s

99.7% вариант находятся в пределах X ± 3s

Отклонение параметра от его средней арифметической в пределах s расценивается как норма, субнормальным считается отклонение в пределах ± 2s и патологическим — сверх этого предела, т.е. > ± 2s» (рис. )

Рис.3 Правило «трех сигм» ( SD – стандартное отклонение).

При распределении Пуассона дисперсия равна средней:

Коэффициент вариации используется при сравнении вариационных рядов, имеющих различную размерность, или одной размерности, но обладающими резкими различиями в своих значениях, затрудняющими их сопоставление.

Вариационный ряд разбивают на четыре интервала, получая, соответственно, 25%, 50% и 75% квантили; 25% и 75% квантили называют также нижним (low quartile) и верхним квартилями(high quartile). 50% квантиль – это медиана. Внутри интерквартильного интервала (между 25% и 75% квантилями) лежат 50% наиболее типичных (близких к центральному) значений.

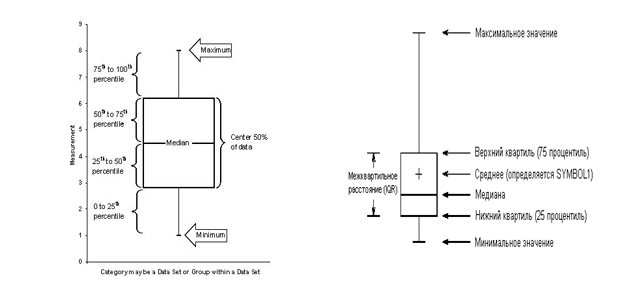
Таким образом, в случае нормального распределения вариационный ряд описывается средней величиной и стандартным отклонением, если распределение неизвестно или оно отлично от нормального, центральную тенденцию и разброс можно описать с помощью медианы, нижнего и верхнего квартиля (интерквартильным интервалом).

Рис.4 Графическое представление описательной статистики (коробчатый график, «коробка с усами», box-plot)

Проверка нормальности распределения

Соответствие экспериментального распределения нормальному проверяется следующими способами:

х ± 0.3 s находится 25 % всех единиц наблюдения;

х ± 0.7 s находится 50 % всех единиц наблюдения;

х ± l,l s находится 75 % всех единиц наблюдения;

х ± 3,0 s находится 99 % всех единиц наблюдения.

— при нормальном распределении, которое обладает симметричностью:

— правило «двух третей» Юла:

а). если распределение симметрично: Me = Mo;

б). если распределение обладает правосторонней асимметрией: Me > Mo;

в). если распределение имеет левостороннюю асимметрией Me 0

в) при левосторонней асимметрии: A _s s × f, то «выскакивающая» варианта исключается из исследования;

Источник

Вариационные ряды

Главная > Учебные материалы > Математика: Вариационные ряды

1.Вариационный ряд. 2.Числовые характеристики вариационного ряда.

1.Вариационный ряд.

Многие явления, в том числе и экономические, имеют большой объем числовой информации. Для того, чтобы обработатать и изучить такой большой объем данных, необходимо сначала каким-то образом его сгруппировать. От того как сгруппировать ряд, зависит какую информацию можно получить в конечном итоге и какими свойствами обладают те или иные признаки (варианты). Вариационный ряд представляет собой сгруппированный ряд числовых данных, ранжированный в порядке возрастания или убывания, каждая группа которого имеет определенный вес (или частоту). Например объем продаж магазином товара за определенный промежуток времени (например за день) можно сгруппировать по наименованию товара.

Таб.1

По данным таблицы построим полигон распределения частот (рис.1)

В приведенной выше таблице проданные товары сгруппированы по наименованию бренда товара (например телевизоры разных марок). Т.е. в данном случае признаком является наименование марки (бренда) товара. Во второй колонке дано количество проданного товара, т.е. частота данного признака. Данный ряд является дискретным. Из графика видно, что наибольшей частотой обладают товары С, D и E. Соответственно 21, 22 и 20 шт.

Таб. 2

По данным таблицы построим гистограмму распределения частот (рис.2)

Таблица 2 сгруппирована по ценовым категориям. Каждая группа имеет свой интервал цен. Данный ряд называется интервальный. Из таблицы можно увидеть, что наибольшее значение частоты имеет группа 3 в интервале цен 40-60 соответственно 43шт. Вариационные ряды на порядок меньше всего объема данных и это существенно облегчает их обработку и анализ. Полигон распределения или гистограмма вариационного ряда является аналогом распределения случайной величины. Несмотря на то, что вариационный ряд имеет существенное преимущество перед полными данными, т.к. он меньше по объему и дает полную информацию об изменении признака и свойствах ряда, на практике бывает достаточно знать лишь некоторые его характеристики.

2.Числовые характеристики вариационного ряда.

Одной из основных числовых характеристик вариационных рядов является средняя арифметическая. Данная величина показывает центральное значение признака, вокруг которого сосредоточенны все наблюдения. Средней арифметической вариационного ряда называется сумма произведений признаков (вариантов) ряда на соответствующие им частости.

Средним линейным отклонением вариационного ряда называется средняя арифметическая модуля отклонения признаков от их средней арифметической.

Дисперсией s 2 вариационного ряда называется средняя арифметическая квадратов отклонений признаков от их средней арифметической.

Среднее квадратическое отклонение вариационного ряда равно квадратному корню из дисперсии.

Важным показателем вариационного ряда является также коэффициент вариации, который показывает однородность исследуемого признака.

Пример.

В компании по продаже бытовой техники, случайная величина Х (цена за единицу товара (техники) в ден.ед.) сгруппирована по интервалам цен и общий объем продаж составил 400 шт. Необходимо построить полигон распределения случайной величины Х, кумуляту и эмпирическую функцию ряда. Необходимо также найти: среднюю арифметическую, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициент вариации, начальный (центральный) моменты k-го порядка, коэффициент асиметрии и эксцесс данной случайной величины.

Решение. Построим таблицу для рассчета средней арифметической и рассчитаем частость для каждого интервала цен.

Как видно из таблицы сумма произведений x i n i = 14610, разделим эту сумму на n и получим среднюю арифметическую вариационного ряда.

По данным таблицы построим гистограмму распределения частот.

Построим и эмпирическую функцию распределения случайной величины (кумуляту).

Из данных таблицы найдем дисперсию, среднее квадратическое отклонение, коэффициент вариации, коэффициент асимметрии и эксцесс по следующим формулам:

Источник

Чем определяется однородность вариационного ряда

Понятие вариационного ряда. Первичные статистические данные, с которыми имеет дело историк, часто представлены неупорядоченной последовательностью чисел, характеризующей ту или иную сторону процесса или явления. В этой совокупности чисел бывает трудно разобраться, и первичная обработка материалов сводится к приведению имеющихся данных к виду, удобному для анализа.

Пример 1. При обследовании студентов первого курса по возрасту были зафиксированы следующие данные:

17 18 18 18 19 18 20 20 19 18 18 21 19 22 23 18 19 19 19 21 21 18 18 18 18 22 19 18 20 18 19 18 20 19 21 20 22 18 19 21 19 19 22 23 19 20 21 22 17 19.

Если упорядочить совокупность исходных данных в убывающем или возрастающем порядке, то получим так называемый ранжированный ряд.

Полученный ряд называется вариационным. Сведение первичных данных в вариационный ряд облегчает анализ совокупности так, например, видно, что в обследованной группе чаще встречаются студенты в возрасте 18-19 лет, меньше всего студентов с крайними для данной группы значениями возрастов (17 лет, 23 года). Кроме того, вариационный ряд является исходным материалом для большинства методов математической статистики.

При построении вариационного ряда можно приписывать вариантам не частоты, а рассматривать доли каждой варианты во всей совокупности. Они вычисляются как отношения соответствующих частот к объему всей совокупности и называются частостями (обозначим их q_i). Частости могут быть выражены в относительных числах или процентах ( см. табл.1 ).

Дискретный и интервальный вариационные ряды. Изменение признака, по которому обследуются объекты, может быть дискретным и непрерывным. Дискретной вариацией признака называется такая, при которой отдельные значения варианты отличаются на некоторую конечную величину. В приведенном примере вариация признака зафиксирована как дискретная (отдельные значения варианты отличаются на единицу). Вариация называется непрерывной, если отдельные значения признака могут отличаться друг от друга на сколько угодно малую величину. Примером непрерывной вариации признака служит распределение посевных площадей по урожайности.

В зависимости от вида вариации различают дискретные и интервальные вариационные ряды. Дискретный признак служит основой для построения дискретного ряда ( см. табл. 1 ). В случае непрерывного признака варианты объединяют в интервалы, образуя интервальный ряд.

В практике исторических исследований непрерывные вариации признака встречаются сравнительно редко, тем не менее, интервальные ряды имеют большое значение в обработке исторических данных. Дело в том, что некоторые признаки, принципиально являясь дискретными, принимают такое большое количество значений, что составленный по ним дискретный ряд является практически необозримым, при этом весьма затрудняется дальнейший его анализ. В такой ситуации прибегают к построению интервального ряда ( см. табл. 2 ).

В интервальном вариационном ряду частоты относятся не к какому-либо отдельному значению признака, а ко всему интервалу. Часто в ходе исследования возникает необходимость интервальный ряд рассматривать как дискретный. В таких случаях за значение признака в интервале берут середину этого интервала (центральное значение).

Принципы построения интервального ряда. Первым шагом при построении интервального вариационного ряда является выбор определенного принципа, который кладется в основу построения интервального ряда. Выбор этого принципа зависит от степени однородности рассматриваемой совокупности.

Ели совокупность однородна, то при построении ряда используют принцип равных интервалов. При этом вопрос об однородности решается содержательным анализом изучаемых явлений.

Следует отметить, что принцип равных интервалов примечается также в тех случаях, когда признак изменяется значительными скачками, природа которых неясна.

Пример 2. Приведем пример вариационного интервального ряда, построенного по принципу равных интервалов ( см. таблицу 2 ).

Если совокупность не совсем однородна, то при построении ряда используют принцип неравных интервалов, при этом стремятся добиться качественной однородности объектов внутри интервалов, например, при построении вариационного ряда распределения в городов и поселков городского типа по числу жителей, применив принцип равных интервалов, мы вынуждены образовать, скажем, такие интервалы: до 50 тыс. жителей, от 50 тыс., до 100 тыс. и т. д., от 450 тыс. до 500 тыс., 500 тыс. и более. Но различия между населенными пунктами, имеющими 3 тыс. жителей и 50 тыс. жителей, безусловно, существеннее, чем такие же по абсолютной величине различия между городами, насчитывающими 453 тыс. и 500 тыс. жителей. Очевидно, что эти данные целесообразно свести в вариационный ряд с неравными интервалами ( см. табл. 3 ), которые объединяют схожие по размерам города и поселки.

Но не всегда удается получить удовлетворительные результаты и с помощью неравных интервалов. Тогда в основу построения интервального ряда кладется социально-экономический критерий, который призван определить типы, однородные в социально-экономическом отношении. Социально-экономический анализ направлен на то, чтобы определить границы интервалов там, где количественное изменение признака приводит к появлению нового качества. Подобный принцип носит название типологического.

Широко использовал типологический принцип в своих статистических исследованиях В. И. Ленин. В частности, анализируя данные германской сельскохозяйственной переписи 1907 г., Ленин вместо 18 групп-интервалов по обеспеченности землей, построенных официальной статистикой, выделил три социально отличные группы хозяйств: пролетарские, крестьянские и капиталистические. Такое выделение позволило выявить степень развития капитализма в сельском хозяйстве Германии ( См.: Ленин В. И. Поли. собр. соч., т. 19, с. 326-330. ).

Наконец, еще более тонким способом группировки является способ специализированного интервала, идея которого принадлежит В. И. Ленину. Суть этого метода заключается в том, что совокупность разбивается на однородные группы (отрасли, типы хозяйства и т. п.) и для каждой группы утроится своя шкала интервалов.

Для того чтобы построить интервальный ряд, после выбора принципа построения нужно определить величину интервала. Величина интервала должна быть такой, чтобы, с одной стороны, ряд не оказался слишком громоздким и, с другой стороны, в нем не исчезали бы особенности изучаемого явления. Величина интервала для ряда с равными интервалами определяется соотношением

где R-размах вариации; k-количество интервалов.

Тогда для подсчета величины интервала достаточно определить количество интервалов. Вопрос о количестве интервалов решается исследователем в каждом конкретном случае в зависимости от поставленной задачи и особенностей исходных данных.

Величину интервала можно подсчитать и непосредственно. Для ряда с равными интервалами может быть предложена следующая приближенная формула для «оптимальной» (наилучшей) величины интервала:

где n-объем совокупности (число элементов совокупности); lgn-десятичный логарифм числа n.

Пример 3. Пусть статистическая совокупность состоит из 400 элементов, наибольшее значение варианты равно 65, наименьшее-5, т. е. в наших обозначениях n=400, x_max=65, x_min=5. Определить величину интервала для этих данных.

Определение величины интервала для ряда, в основу построения которого положен не принцип равных интервалов, должно базироваться на знании исходного материала, универсальных рекомендаций в этом случае дать не возможности.

Закономерность распределения признака. Анализ вариационного ряда начинается с выявления зависимости между вариантами и частотами (частотами).

В случае неравных интервалов закономерность соотношения между вариантами и частотами (частотами) может не проявиться или же иметь искаженный вид. Поэтому для рядов с неравными интервалами необходимо обеспечить сравнимость частот (частоты), что достигается вычислением плотности распределения.

Плотность распределения рассчитывается как отношение частоты (n_i) или частоcти (q_i) к величине соответствующего интервала (h_i). В зависимости от того, какое берется соотношение, различают абсолютную и относительнуюплотности распределения:

Пример 4. В табл. 4 дано распределение крестьянских хозяйств Актюбинского уезда по величине посева. Анализируя изменение частоты, мы заметим, что самой многочисленной является группа хозяйств, имеющих размер посева от 5 до 10 дес. Примерно в полтора раза меньше хозяйств с посевом от 3 до 5 дес. Группа хозяйств с размером посева от 15 до 25 дес. превосходит группу хозяйств, засевающих от 10 до 15 дес. Эти выводы верны для групп, но не могут дать верного представления о фактическом распределении признака. Дело в том, что группы (интервалы), которые мы рассматриваем, неодинаковы, более крупные из них уже в силу своей величины могут содержать в себе большее число хозяйств, чем менее крупные. Чтобы избавиться от искажающего влияния неравных интервалов и сделать частоты сопоставимыми, рассчитаем плотности распределения, т. е. вычислим, сколько хозяйств приходится на единицу интервала ( столбец 4-й табл. 4 ).

После обеспечения сравнимости частот видим несколько иную картину. Плотность, возрастая, достигает максимального значения на интервале 3-5 и затем постепенно убывает. Значит, самой многочисленной в переводе на единицу группировочного признака является группа хозяйств с посевами от 3 до 5 дес.

Однако и в случае, когда сравнимость обеспечена, закономерность ряда, если даже таковая имеется, не всегда выступает как очевидная. Так, при небольшом числе наблюдений часто не удается получить явно выраженную закономерность. Иногда помочь ее выявлению может укрупнение интервалов.

Расщепление интервалов. Существуют способы расщепления интервалов, используемые при различных предположениях относительно распределения признака. Мы ограничимся рассмотрением простейшего-случая, когда признак в интервалах распределен равномерно ( Способы расщепления интервалов в предположении, что, признав, изменяется по параболе 2-го порядка, изложены в кн.: Венецкий И. Г., Кильдишев Г. С. Основы теории вероятностей и математической статистики. М., 1968 ).

В. И. Ленин поясняет используемый им прием дробления (расщепления) интервалов на условном примере. Пусты, имеется пять групп такого размера от низшей к высшей: 30, 25, 20, 15 и 10% дворов, им соответствуют такие процентные доли посева: 15, 20, 20, 21 и 24%. Для того чтобы в низшей группе было 50% дворов, необходимо к первой из пяти групп прибавить 20% из второй группы, т. е. 4 /₅ второй группы: 30+25* 4 /₅=50%.

Чтобы соотношение между группами не изменилось (здесь мы пользуемся предположением о том, что признак распределен равномерно), нужно из процентной доли посева второй группы выделить также ее и присоединить к первой группе: 15+20o 4 /₅=31%.

Основные характеристики вариационного ряда

Построение вариационного ряда является только первым шагом в изучении статистических данных. Для более глубокого исследования материала необходимы обобщающие количественные показатели, вскрывающие общие свойства статистической совокупности. Эти показатели, во-первых, дают общую картину, показывают тенденцию развития процесса или явления, нивелируя случайные индивидуальные отклонения, во-вторых, позволяют сравнивать вариационные ряды и, наконец, используются во всех разделах математической статистики при более полном и сложном математическом анализе статистической совокупности.

Существуют две группы характеристик вариационного ряда: 1) меры уровня, или средние, 2) меры рассеяния.

Меры уровня, или средние. Наиболее употребительными в статистических исследованиях являются три вида средних: средняя арифметическая, мода и медиана.

Выбор типа средней для характеристики вариационного ряда зависит от цели, для которой исчисляется средняя, от особенностей исходного материала и от возможностей той или иной средней.

Прежде чем перейти к характеристике отдельных видов средней, сформулируем некоторые, самые общие требования к средней.

Средняя, представляет собой количественную характеристику качественно однородной совокупности. Нарушение этого требования приводит к неверным выводам, искажает суть явления.

Кроме того, необходимо, чтобы средняя не была слишком абстрактной, а имела ясный смысл в решении задачи.

Далее, желательно, чтобы процедура вычисления средней была проста. При прочих равных условиях предпочтение отдается той средней, которая проще вычисляется.

И, наконец, при выборе средней желательно свести к минимуму влияние случайных колебаний выборки. Так, если одной и той же совокупности взять несколько групп элементов, то средние, им соответствующие, будут, как правило, различаться по величине. Рекомендуется использовать вид средней, у которой эти различия минимальны ( подробнее о выборке и выборочной средней см. гл. 5 данного раздела ).

Пример 5. Вычислим среднюю арифметическую для данных табл.

Средняя арифметическая интервального вариационного ряда вычисляется следующим образом: за значение признака принимается середина интервала (центральное значение), которая рассчитывается как арифметическая средняя границ интервала. Часто вычисление средней арифметической для интервального вариационного ряда осложняется тем, что неизвестны или нижняя граница первого интервала, или верхняя граница последнего интервала, или та и другая одновременно. В таких случаях иногда (Впрочем, в таких случаях часто отказываются oт исчисления средней арифметической, заменяя ее модой или медианой) условно предполагают, что интервальная разность неопределенного интервала такая же, что и у рядом стоящего, и на основе этого предположения устанавливают границы крайних интервалов.

Пример 6. Вычислим средние размеры наделов крестьян по данным табл. 5.

Для решения задачи, прежде всего, необходимо найти середины интервалов. Определенная трудность возникает в связи с тем, что первый и последний интервалы являются открытыми. Нижнюю границу первого интервала естественно принять равной нулю. Тогда середина этого интервала равна (0+2)/2=l. Для нахождения центрального значения последнего интервала применим предложенный выше прием. Величина интервала, предшествующего последнему, равна 2. Условно принимаем за величину последнего интервала 2. Тогда верхняя граница того интервала-9 и, следовательно, его середина вычисляется так: (7+9)/2=8.

Пользуясь формулой средней арифметической (4.4а) и принимая за значение признака середину интервала (строка 2 табл. 5), рассчитываем средний дореформенный надел у барщинных крестьян:

Аналогично вычисляется средний дореформенный надел у оброчных крестьян: .

Медианой (обозначим M_е) называется такое значение варьирующего признака, которое приходится на середину вариационного ряда.

При нахождении медианы дискретного вариационного ряда могут возникнуть два случая: 1) число вариант нечетно (k=2m+1), 2) число вариант четно (k=2m). В первом случае M_e=x_m+1, т. е. медиана равна центральной (срединной) варианте ряда, во втором случае M_e,=(x_m+x_m+1)/2, т.е. медиана принимается равной полу сумме находящихся в середине ряда вариант.

Пример 7. Пусть дан ряд с нечетным числом вариант:

Источник