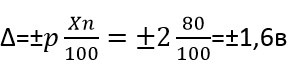чем определяется классификация средств измерений по классам точности

Что нужно знать о классе точности измерительного прибора?

Измерительные приборы: вольтметры, амперметры, токовые клещи, осциллографы и другие — это устройства, предназначенные для определения искомых величин в заданном диапазоне, каждый из них имеет свою точность, причем устройства, измеряющие одну и ту же величину, в зависимости от модели, могут отличаться по точности и классу.

В каких-то ситуациях достаточно просто определить значение, например, вольтаж батарейки, а в других необходимо выполнить многократное повторение измерений высокоточными приборами для получения максимально достоверного результата, так в чем отличие таких измерительных устройств, что означает класс точности, сколько их бывает, как его определить и многое другое читайте далее в нашей статье.

Что такое класс точности

Определение: «Класс точности измерения — это общая характеристика точности средства измерения, определяемая пределами допустимых основных и дополнительных погрешностей, а также другими факторами, влияющими на нее».

Сам по себе класс не является постоянной величиной измерения, потому что само измерение зачастую зависит от множества переменных: места измерения, температуры, влажности и других факторов, класс позволяет определить лишь только в каком диапазоне относительных погрешностей работает данный прибор.

Чтобы заранее оценить погрешность, которую измерит устройство, также могут использоваться нормативные справочные значения.

Относительная погрешность — это отношение абсолютной погрешности к модулю действительного приближенного показателя полученного значения, измеряется в %.

Абсолютная погрешность рассчитывается следующим образом:

∆=±a или ∆=(a+bx)

x – число делений, нормирующее значение величины

a, b – положительные числа, не зависящие от х

Абсолютная и приведенная погрешность рассчитывается по следующим формулам, см. таблицу ниже

Какие классы точности бывают, как обозначаются

Как мы уже успели выяснить, интервал погрешности определяется классом точности. Данная величина рассчитывается, устанавливается ГОСТом и техническими условиями. В зависимости от заданной погрешность, бывает: абсолютная, приведенная, относительная, см. таблицу ниже

Согласно ГОСТ 8.401-80 в системе СИ классы точности обычно помечается латинской буквой, часто с добавлением индекса, отмеченного цифрой. Чем меньше погрешность, соответственно, меньше цифра и буквенное значение выше по алфавиту, тем более высокая точность.

Класс точности обозначается на корпусе устройства в виде числа обведенного в кружок, обозначает диапазон погрешностей измерений в процентах. Например, цифра ② означает относительную погрешность ±2%. Если рядом со знаком присутствует значок в виде галочки, это значит, что длина шкалы используется в качестве вспомогательного определения погрешности.

Каким ГОСТом регламентируется точность приборов?

ГОСТ 8.401-80 «Классы точности средств измерений» общие требования. Нормативным документом устанавливаются общие положения классификации точностей измерительных приборов.

Как определить класс точности электроизмерительного прибора, формулы расчета

Чтобы определить класс точности, необходимо взглянуть на его корпус или инструкцию пользователя, в ней вы можете увидеть цифру, обведенную в круг, например, ① это означает, что ваш прибор измеряет величину с относительной погрешностью ±1%.

Но что делать если известна относительная погрешность и необходимо рассчитать класс точности, например, амперметра, вольтметра и т.д. Рассмотрим на примере амперметра: известна ∆x=базовая (абсолютная) погрешность 0,025 (см. в инструкции), количество делений х=12

Находим относительную погрешность:

Y= 100×0,025/12=0,208 или 2,08%

(вывод: класс точности – 2,5).

Следует отметить, что погрешность неравномерна на всем диапазоне шкалы, измеряя малую величину вы можете получить наибольшую неточность и с увеличением искомой величины она уменьшается, для примера рассмотрим следующий вариант:

Вольтметр с классом p=±2, верхний предел показаний прибора Xn=80В, число делений x=12

Предел абсолютной допустимой погрешности:

Относительная погрешность одного деления:

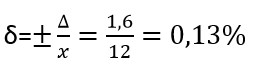
Если вам необходимо выполнить более подробный расчет, смотрите ГОСТ 8.401-80 п.3.2.6.

Поверка приборов, для чего она нужна

Все измерительные приборы измеряют с некой погрешностью, класс точности говорит лишь о том, в каком диапазоне она находится. Бывают случаи, когда диапазон погрешности незаметно увеличивается, и мы начинаем замечать, что измеритель «по-простому» начинает врать. В таких случаях помогает поверка.

Это процесс измерения эталонной величины в идеальных условиях прибором, обычно проводится метрологической службой или в метрологическом отделе предприятия производителя.

Существует первичная и периодическая, первичную проверку проводят после выпуска изделия и выдают сертификат, периодическую проводят не реже чем раз в год, для ответственных приборов чаще.

Поэтому если вы сомневаетесь в правильности работы устройства, вам следует провести его поверку в ближайшей метрологической службе, потому что измеритель может врать как в меньшую, так и в большую сторону.

Как легко проверить потребление электроэнергии в квартире, можете узнать в нашей статье.

Видео на тему относительная погрешность прибора

Заключение

Класс точности является важным показателем для каждого прибора, при выборе всегда обращайте внимание на него. Если вам нужен, например, электрический счетчик, важно чтобы он измерял потребление энергии с максимальной точностью, благодаря этому за весь период эксплуатации, вы сможете сэкономить приличную сумму средств.

Но, а если вам необходимо просто периодически проверять напряжение в розетке, для этого не стоит переплачивать за дорогостоящую покупку.

Источник

Метрология, стандартизация и сертификация

Лекция 2. Виды и методы измерений

1. Основные понятия и определения. Виды измерений.

2. Методы измерений.

3. Понятие о точности измерений.

4. Основы обеспечения единства измерений

1. Основные понятия и определения. Виды измерений

Измерение — совокупность операций по применению системы измерений для получения значения измеряемой физической величины.

Измерения могут быть классифицированы по метрологическому назначению на три категории:

Ненормированные – измерения при ненормированных метрологических характеристиках.

Технические – измерения при помощи рабочих средств измерений.

Метрологические – измерения при помощи эталонов и образцовых средств измерений.

Ненормированные измерения наиболее простые. В них не нормируются точность и достоверность результата. Поэтому область их применения ограничена. Они не могут быть применены в области, на которую распространяется требование единства измерений. Каждый из нас выполнял ненормированные измерения длины, массы, времени, температуры не задумываясь о точности и достоверности результата. Как правило, результаты ненормированных измерений применяются индивидуально, т.е. используются субъектом в собственных целях.

Технические измерения удовлетворяют требованиям единства измерений, т.е. результат бывает получен с известной погрешностью и вероятностью, записывается в установленных единицах физических величин, с определённым количеством значащих цифр. Выполняются при помощи средств измерений с назначенным классом точности, прошедших поверку или калибровку в метрологической службе. В зависимости от того, предназначены измерения для внутрипроизводственных целей или их результаты будут доступны для всеобщего применения, необходимо выполнение калибровки или поверки средств измерений. Средство измерений, прошедшее калибровку или поверку, называют рабочим средством измерений. Примером технических измерений является большинство производственных измерений, измерение квартирными счётчиками потреблённой электроэнергии, измерения при взвешивании в торговых центрах, финансовые измерения в банковских терминалах. Средство измерений, применяемое для калибровки других средств измерений, называют образцовым средством измерений. Образцовое средство измерений имеет повышенный класс точности и хранится отдельно, для технических измерений не применяется.

Метрологические измерения не просто удовлетворяют требованиям единства измерений, а являются одним из средств обеспечения единства измерений. Выполняются с целью воспроизведения единиц физических величин для передачи их размера образцовым и рабочим средствам измерений. Метрологические измерения выполняет метрологическая служба в стандартных условиях, сертифицированным персоналом.

В дисциплине «Метрология, стандартизация и сертификация» рассматриваются технические измерения.

Можно выделить следующие виды измерений.

1) По характеру зависимости измеряемой величины от времени методы измерений подразделяются на:

2) По способу получения результатов измерений (виду уравнений измерений) методы измерений разделяют на прямые, косвенные, совокупные и совместные.

При прямом измерении искомое значение величины находят непо­средственно из опытных данных (например, измерение диаметра штан­генциркулем).

При косвенном измерении искомое значение величины определяют на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям.

Совместными называют измерения двух или нескольких не одноимённых величин, производимые одновременно с целью нахождения функциональной зависимости между величинами (например, зависимости длины тела от температуры).

Совокупные – это такие измерения, в которых значения измеряемых величин находят по данным повторных измерений одной или нескольких одноименных величин (при различных сочетаниях мер или этих величин) путем решения системы уравнений.

3) По условиям, определяющим точность результата измерения, мето­ды делятся на три класса.

Измерении максимально возможной точности (например, эталонные измерения), достижимой при существующем уровне техники.

Контрольно-поверочные измерения, погрешность которых с определенной вероятностью не должна превышать некоторое заданное значение.

Технические измерения, в которых погрешность результата определяется характеристиками средств измерения.

4) По способу выражения результатов измерений различают абсолютные и относительные измерения.

Абсолютное измерение основано на прямых измерениях величины и (или) использования значений физических констант.

При относительных измерениях величину сравнивают с одноименной, играющей роль единицы или принятой за исходную (например, измерение диаметра вращающейся детали по числу оборотов соприкасающегося с ней аттестованного ролика).

5) В зависимости от совокупности измеряемых параметров изделия различают поэлементный и комплексный методы измерения.

Поэлементный метод характеризуется измерением каждого параметра изделия в отдельности (например, эксцентриситета, овальности, огранки цилиндрического вала).

Комплексный метод характеризуется измерением суммарного пока­зателя качества (а не физической величины), на который оказывают влияние отдельные его составляющие (например, измерение радиального биения цилиндрической детали, на которое влияют эксцентриситет, овальность и др.).

Источник

Чем определяется классификация средств измерений по классам точности

Государственная система обеспечения единства измерений

КЛАССЫ ТОЧНОСТИ СРЕДСТВ ИЗМЕРЕНИЙ

State system for ensuring the uniformity of measurements. Accuracy classes of measuring instruments. General requirements

Дата введения 1981-07-01

Постановлением Государственного комитета СССР по стандартам от 12 ноября 1980 г. N 5320 дата введения установлена 01.07.81

ПЕРЕИЗДАНИЕ. Октябрь 2010 г.

Настоящий стандарт устанавливает общие положения деления средств измерений на классы точности, способы нормирования метрологических характеристик, комплекс требований к которым зависит от класса точности средств измерений, и обозначения классов точности.

Стандарт не устанавливает классы точности средств измерений, для которых в стандартах предусмотрены нормы отдельно для систематической и случайной составляющих погрешности, а также нормирование номинальных функций влияния, если средства измерений предназначены для применения без введения поправок с целью исключения дополнительных погрешностей с учетом номинальных функций влияния. Стандарт не устанавливает также классы точности средств измерений, при применении которых в соответствии с их назначением необходимо для оценки погрешности измерений учитывать динамические характеристики.

Пояснение терминов, используемых в настоящем стандарте, приведено в приложении 4.

Стандарт полностью соответствует международной рекомендации МОЗМ N 34*.

1. ОБЩИЕ ПОЛОЖЕНИЯ

1.1. Классы точности следует устанавливать в стандартах или технических условиях, содержащих технические требования к средствам измерений, подразделяемым по точности. Необходимость подразделения средств измерений по точности определяют при разработке этой документации.

1.1.1. Классы точности средств измерений конкретного вида следует устанавливать в стандартах общих технических требований (технических требований) или общих технических условий (технических условий).

1.1.2. Классы точности средств измерений конкретного типа следует выбирать из ряда классов точности для средств измерений конкретного вида, регламентированного в стандартах, и устанавливать в стандартах технических требований (условий) или в технической документации, утвержденной в установленном порядке.

1.1.3. В стандартах или технических условиях, устанавливающих класс точности средств измерений конкретного типа, следует давать ссылку на стандарт, которым установлен ряд классов точности на средства измерений данного вида.

1.2. Для каждого класса точности в стандартах на средства измерений конкретного вида устанавливают конкретные требования к метрологическим характеристикам, в совокупности отражающие уровень точности средств измерений этого класса. Для малоизменяющихся метрологических характеристик допускается устанавливать требования, единые для двух и более классов точности.

Независимо от классов точности нормируют метрологические характеристики, требования к которым целесообразно устанавливать едиными для средств измерений всех классов точности, например входные или выходные сопротивления.

Совокупности нормируемых метрологических характеристик должны быть составлены из характеристик, предусмотренных ГОСТ 8.009-84. Допускается включать дополнительные характеристики.

Примеры составления совокупности нормируемых метрологических характеристик, требования к которым устанавливают в зависимости от классов точности средств измерений, приведены в приложении 1.

1.3. Средствам измерений с двумя или более диапазонами измерений одной и той же физической величины допускается присваивать два или более класса точности (см. приложение 2, п.1).

1.4. Средствам измерений, предназначенным для измерений двух или более физических величин, допускается присваивать различные классы точности для каждой измеряемой величины (см. приложение 2, п.2).

1.5. С целью ограничения номенклатуры средств измерений по точности для средств измерений конкретного вида следует устанавливать ограниченное число классов точности, определяемое технико-экономическими обоснованиями.

1.6. Средства измерений должны удовлетворять требованиям к метрологическим характеристикам, установленным для присвоенного им класса точности, как при выпуске их из производства, так и в процессе эксплуатации.

1.7. Классы точности цифровых измерительных приборов со встроенными вычислительными устройствами для дополнительной обработки результатов измерений следует устанавливать без учета режима обработки.

1.8. Классы точности следует присваивать средствам измерений при их разработке с учетом результатов государственных приемочных испытаний. Если в стандарте или технических условиях, регламентирующих технические требования к средствам измерений конкретного типа, установлено несколько классов точности, то допускается присваивать класс точности при выпуске из производства, а также понижать класс точности по результатам поверки в порядке, предусмотренном документацией, регламентирующей поверку средств измерений. При этом класс точности набора мер определяется классом точности меры с наибольшей погрешностью (см. приложение 2, п.3).

2. СПОСОБЫ НОРМИРОВАНИЯ И ФОРМЫ ВЫРАЖЕНИЯ МЕТРОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК

2.1. Требования следует устанавливать к каждой нормируемой характеристике отдельно.

2.2. Пределы допускаемых основной и дополнительных погрешностей следует выражать в форме приведенных, относительных или абсолютных погрешностей в зависимости от характера изменения погрешностей в пределах диапазона измерений, а также от условий применения и назначения средств измерений конкретного вида (см. приложение 3). Пределы допускаемой дополнительной погрешности допускается выражать в форме, отличной от формы выражения пределов допускаемой основной погрешности.

Примечание. Выражение пределов допускаемой погрешности в форме приведенных и относительных погрешностей является предпочтительным, так как они позволяют выражать пределы допускаемой погрешности числом, которое остается одним и тем же (числами, которые остаются одними и теми же) для средств измерений одного уровня точности, но с различными верхними пределами измерений.

2.3. Пределы допускаемой основной погрешности устанавливают в последовательности, приведенной ниже.

2.3.1. Пределы допускаемой абсолютной основной погрешности устанавливают по формуле

(1)

, (2)

— значение измеряемой величины на входе (выходе) средств измерений или число делений, отсчитанных по шкале;

В обоснованных случаях пределы допускаемой абсолютной погрешности устанавливают по более сложной формуле или в виде графика либо таблицы.

Примечание. При применении формулы (1) или (2) для средств измерений, используемых с отсчитыванием интервалов между произвольно выбираемыми отметками шкалы, допускается указывать, что погрешность каждого отдельного средства измерений не должна превышать установленной нормы, оставаясь только положительной или только отрицательной.

2.3.2. Пределы допускаемой приведенной основной погрешности следует устанавливать по формуле

, (3)

— пределы допускаемой абсолютной основной погрешности, устанавливаемые по формуле (1);

— нормирующее значение, выраженное в тех же единицах, что и ;

Значения, указанные в скобках, не устанавливают для вновь разрабатываемых средств измерений.

При одном и том же показателе степени допускается устанавливать не более пяти различных пределов допускаемой основной погрешности для средств измерений конкретного вида.

2.3.3. Нормирующее значение для средств измерений с равномерной, практически равномерной или степенной шкалой (см. приложение 4), а также для измерительных преобразователей, если нулевое значение входного (выходного) сигнала находится на краю или вне диапазона измерений, следует устанавливать равным большему из пределов измерений или равным большему из модулей пределов измерений, если нулевое значение находится внутри диапазона измерений.

Для электроизмерительных приборов с равномерной, практически равномерной или степенной шкалой и нулевой отметкой внутри диапазона измерений нормирующее значение допускается устанавливать равным сумме модулей пределов измерений.

2.3.4. Для средств измерений физической величины, для которых принята шкала с условным нулем, нормирующее значение устанавливают равным модулю разности пределов измерений (см. приложение 2, п.4).

2.3.5. Для средств измерений с установленным номинальным значением нормирующее значение устанавливают равным этому номинальному значению (см. приложение 2, п.5).

2.3.6. Для измерительных приборов с существенно неравномерной шкалой нормирующее значение устанавливают равным всей длине шкалы или ее части, соответствующей диапазону измерений. В этом случае пределы абсолютной погрешности выражают, как и длину шкалы, в единицах длины.

2.3.7. В случаях, не предусмотренных в пп.2.3.3-2.3.6, указания по выбору нормирующего значения должны быть приведены в стандартах на средства измерений конкретного вида.

2.3.8. Пределы допускаемой относительной основной погрешности устанавливают по формуле

, (4)

если установлено по формуле (1),

, (5)

— отвлеченное положительное число, выбираемое из ряда, приведенного в п.2.3.2;

— больший (по модулю) из пределов измерений;

;

В обоснованных случаях пределы допускаемой относительной основной погрешности устанавливают по более сложной формуле или в виде графика либо таблицы.

Соотношение между числами и следует устанавливать в стандартах на средства измерений конкретного вида.

2.4. Пределы допускаемых дополнительных погрешностей устанавливают:

в виде постоянного значения для всей рабочей области влияющей величины или в виде постоянных значений по интервалам рабочей области влияющей величины;

путем указания отношения предела допускаемой дополнительной погрешности, соответствующего регламентированному интервалу влияющей величины, к этому интервалу;

Источник

Мокров Ю. Метрология, стандартизация, сертификация

ОГЛАВЛЕНИЕ

Глава 3. Cредства измерений и их свойства

Измерения выполняются с помощью технических средств, которые называются средствами измерений (СИ). Разработка СИ является задачей приборостроения. В метрологии СИ рассмат-риваются с точки зрения их единой классификации и выявления параметров, которые обеспечивают получение результата измерений с заданной точностью. Здесь же рассматриваются методы и средства передачи размеров единиц от эталонов к рабочим средствам измерений.

Оценка пригодности средств измерений для решения тех или иных измерительных задач проводится путем рассмотрения их метрологических характеристик.
Метрологическая характеристика (МХ) – характеристика одного из свойств средства измерений, влияющая на результат измерений и его погрешность. Метрологические характеристики позволяют судить об их пригодности для измерений в известном диапазоне с известной точностью. Метрологические характеристики, устанавливаемые нормативными документами на средства измерений, называют нормируемыми метрологическими характеристиками, а определяемые экспериментально – действи-тельными.
Для каждого типа СИ устанавливаются свои метрологические характеристики. Ниже рассматриваются наиболее распространенные на практике метрологические характеристики.
Диапазон измерений СИ – область значений величины, в пределах которой нормированы его допускаемые пределы погрешности. Для мер это их номинальное значение, для преобразователей — диапазон преобразования. Различают нижний и верхний пределы измерений, которые выражаются значениями величины, ограничивающими диапазон измерений снизу и сверху.
Погрешность СИ — разность между показанием средства измерений – Хп и истинным (действительным) значением измеряемой величины – Х д.
Существует распространенная классификация погрешностей средств измерений. Ниже приводятся примеры их наиболее часто используемых видов.
Абсолютная погрешность СИ – погрешность средства измерений, выраженная в единицах измеряемой величины: DХ = Хп – Хд. Абсолютная погрешность удобна для практического применения, т.к. дает значение погрешности в единицах измеряемой величины. Но при ее использовании трудно сравнивать по точности приборы с разными диапазонами измерений. Эта проблема снимается при использовании относительных погрешностей.
Если абсолютная погрешность не изменяется во всем диапазоне измерения, то она называется аддитивной, если она изменяется пропорционально измеряемой величине (увеличивается с ее увеличением), то она называется мультипликативной
Относительная погрешность СИ – погрешность средства измерений, выраженная отношением абсолютной погрешности СИ к результату измерений или к действительному значению измеренной величины: d = DХ / Хд. Относительная погрешность дает наилучшее из всех видов погрешностей представление об уровне точности измерений, который может быть достигнут при использовании данного средства измерений. Однако она обычно существенно изменяется вдоль шкалы прибора, например, увеличивается с уменьшением значения измеряемой величины. В связи с этим часто используют приведенную погрешность.
Приведенная погрешность СИ – относительная погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины ХN, которое называют нормирующим: g = DХ / ХN..
Относительные и приведенные погрешности обычно выражают либо в процентах, либо в относительных единицах (долях единицы).
Для показывающих приборов нормирующее значение устанавливается в зависимости от особенностей и характера шкалы. Приведенные погрешности позволяют сравнивать по точности средства измерений, имеющие разные пределы измерений, если абсолютные погрешности каждого из них не зависят от значения измеряемой величины.
По условиям проведения измерений погрешности средств измерений подразделяются на основные и дополнительные.
Основная погрешность СИ – погрешность средства измерений, применяемого в нормальных условиях, т.е. в условиях, которые определены в НТД не него как нормальные. Нормальные значения влияющих величин указываются в стандартах или технических условиях на средства измерений данного вида в форме номиналов с нормированными отклонениями. Наиболее типичными нормальными условиями являются:

— относительная влажность (65±15) %;

Иногда вместо номинальных значений влияющих величин указывается нормальная область их значений. Например, влажность (30 – 80) %.
Дополнительная погрешность СИ – составляющая погрешности СИ, возникающая дополнительно к основной погрешности вследствие отклонения какой-либо из влияющих величин от нормального ее значения. Деление погрешностей на основные и дополнительные обусловлено тем, что свойства средств измерений зависят от внешних условий.
Погрешности по своему происхождению разделяются на систематические и случайные.
Систематическая погрешность СИ – составляющая погрешности средства измерений, принимаемая за постоянную или закономерно изменяющуюся. Систематические погрешности являются в общем случае функциями измеряемой величины и влияющих величин (температуры, влажности, давления, напряжения питания и т.п.).
Случайная погрешность СИ – составляющая погрешности средства измерений, изменяющаяся случайным образом. Случайные погрешности средств измерений обусловлены случайными изменениями параметров составляющих эти СИ элементов и случайными погрешностями отсчета показаний приборов.
При конструировании прибора его случайную погрешность стараются сделать незначительной в сравнении с другими погрешностями. У хорошо сконструированного и выполненного прибора случайная погрешность незначительна. Однако при увеличении чувствительности средств измерений обычно наблюдается увеличение случайной погрешности. Тогда при повторных измерениях одной и той же величины в одних и тех же условиях результаты будут различными. В таком случае приходится прибегать многократным измерениям и к статистической обработке получаемых результатов. Как правило, случайную погрешность приборов снижается до такого уровня, что проводить многократные измерений нет необходимости.
Стабильность СИ — качественная характеристика средства измерений, отражающая неизменность во времени его метрологических характеристик.
Градуировочная характеристика СИ – зависимость между значениями величин на входе и выходе средства измерений, полученная экспериментально. Может быть выражена в виде формулы, графика или таблицы.

3.3 Использование СИ

Средства измерений можно использовать только тогда, когда известны их метрологические характеристики. Обычно указываются номинальные значения параметров средств измерений и допускаемые отклонения от них. Сведения о метрологических характеристиках приводятся в технической документации на средства измерений или указываются на них самих. Как правило, реальные метрологические характеристики имеют отклонения от их номинальных значений. Поэтому устанавливают границы для отклонений реальных метрологических характеристик от номинальных значений – нормируют их. Нормирование метрологических характеристик средств измерений позволяет избежать произвольного установления их характеристик разработчиками.
C помощью нормируемых метрологических характеристик решаются следующие основные задачи:

Нормирование характеристик СИ проводится в соответствии с положениями стандартов. Например, ГОСТ 8.009-84 «ГСИ. Нормируемые метрологические характеристики средств измерений». Соответствие средств измерений установленным для них нормам делает эти средства взаимозаменяемыми.
Одной из важнейших метрологических характеристик СИ является их погрешность, знание которой необходимо для оценивания погрешности измерения.
Необходимо отметить, что погрешность СИ является только одной из составляющих погрешности результата измерений, получаемого с использованием данного СИ. Другими составляющими являются погрешность метода измерений и погрешность оператора, проводящего измерения.
Погрешности средств измерений могут быть обусловлены различными причинами:

3.5 Класс точности СИ и его обозначение

Установление рядов пределов допускаемых погрешностей позволяет упорядочить требования к средствам измерений по точности. Это упорядочивание осуществляется путем установления классов точности СИ.
Класс точности СИ – обобщенная характеристика данного типа СИ, отражающая уровень их точности, выражаемая пределами допускаемой основной, а в некоторых случаях и дополнительных погрешностей (они рассмотрены выше), а также другими характеристиками, влияющими на точность. Класс точности применяется для средств измерений, используемых в технических измерениях, когда нет необходимости или возможности выделить отдельно систематические и случайные погрешности, оценить вклад влияющих величин с помощью дополнительных погрешностей. Класс точности позволяет судить о том, в каких пределах находится погрешность средств измерений одного типа, но не является непосредственным показателем точности измерений, выполняемых с помощью каждого из этих средств. Класс точности СИ конкретного типа устанавливают в стандартах технических требований или других нормативных документах.
При выражении предела допускаемой основной погрешности в форме абсолютной погрешности класс точности в документации и на средствах измерения обозначается прописными буквами латинского алфавита или римскими цифрами. Чем дальше буква от начала алфавита, тем больше погрешность. Расшифровка соответ-ствия букв значению абсолютной погрешности осуществляется в технической документации на средство измерения.
Выражение класса точности через относительные и приведенную погрешности рассмотрено в предыдущем разделе
В настоящее время по отношению к современным средствам измерений понятие класс точности применяется довольно редко. В основном он чаще всего используется для описания характеристик электроизмерительных приборов, аналоговых стрелочных приборов всех типов, некоторых мер длины, весов, гирь общего назначения, манометров.
Примеры обозначение классов точности для различных форм выражения погрешности приведены в таблице.

Обозначение классов точности

___________________________________________________________
Пределы допускаемой Обозначения Форма выраже-
основной погрешности ния погрешности
в документации на приборе
g = ± 1,5 Класс точности 1,5 1,5 Приведенная
погрешность

d = ± 0,5 Класс точности 0,5 0,5 Относительная
погрешность,
постоянная

d = ± [ 0,02 + 0,01( xk/x –1)] Класс точности 0,02/0,01 Относительная
0,02/0,01 погрешность,
возрастает с
уменьшением х

Результаты калибровки удостоверяются калибровочным знаком, наносимым на СИ, или сертификатом о калибровке. Калибровке присущ ряд особенностей по сравнению с поверкой. Это добровольная процедура и она может выполняться любой метрологической службой. При этом аккредитация на право калибровки также является добровольной (не обязательной) процедурой.
Отмеченные особенности калибровки являются следствием разгосударствления процессов контроля за метрологической исправностью средств измерений – отказом от их всеобщей обязательности поверки.
Хотя калибровка может проводиться любой метрологической службой и является добровольной процедурой, для ее проведения необходимы определенные условия. Основное из них – прослеживание измерений, т.е. обязательная передача размера единицы от эталона к калибруемому рабочему средству измерений.
Для организации работ по калибровке в РФ создана Российская система калибровки (РСК), в которую входят государственные научные метрологические центры, органы ГМС, метрологические службы юридических лиц, объединенные целью ОЕИ в сферах, не подлежащих государственному метрологическому контролю и надзору.
Российская система калибровки базируется на следующих принципах:

Источник