чем определяется число направляемых мод в волоконных световодах
Чем определяется число направляемых мод в волоконных световодах
В следующем разделе обсуждаются различные моды оптических волокон и эффекты модовой дисперсии.
3.4.2. Модовая дисперсия
Важно для начала рассмотреть природу и свойства модовой передачи. У волокна с большое апертурой и/или диаметром будет большое число мод (лучей света), распространяющихся на протяжении этого волокна. Ненаправленный источник света (то есть такой, который одинаков излучает лучи во всех направлениях) вроде светодиода в одном импульсе излучает несколько тысяч световых лучей. Поскольку источник света вводит в сердечник пучок света с больше, углом, каждая мода света, распространяющаяся вдоль волокна с отличающимся углом, пройдет различное расстояние. Следовательно, время прохождения волокна от начала до конца будет для различных лучей разным. Световой передатчик вводит в волокно все моды одновременно, сигнал в начале волокна выглядит в виде короткого острого импульса. К тому времени, когда сигнал достигнет конца волокна, он растянется и будет выглядеть как удлиненный импульс. Это явление называется «модовой дисперсией» (рис. 3.13).
Рис. 3.13. Эффект дисперсии импульса вследствие многомодового распространения
Иллюстрация к межмодовой дисперсии на странице → Многомодовое оптоволокно
Если входные импульсы расположены близко друг к другу, выходные импульсы начнут перекрываться друг с другом, вызывая в приемнике интерференцию различных символов. Эта ситуация затрудняет различение импульсов приемником и создает ошибки данных. Это главный фактор, ограничивающий скорости передачи в многомодовых типах волоконно-оптических кабелей (рис. 3.14).
Рис. 3.14. Межсимвольная интерференция вследствие модовой дисперсии
Из этой диаграммы можно видеть, что приемнику будет трудно различить выходные импульсы, когда они на выходе из сердечника волокна перекроют друг друга (межсимвольная интерференция).
Модовая дисперсия измеряется в наносекундах и вычисляется по следующей формуле:
Модовая дисперсия возрастает с увеличением числовой апертуры, следовательно, полоса пропускания волокна снижается с увеличением апертуры. То же правило применимо к увеличению диаметра волокна. Это показано на графике на рис. 3.15.
Поставщики кабелей указывают в технических характеристиках кабеля величину дисперсии. В качестве единиц измерения используется время удлинения импульса в пикосекундах (или наносекундах) на километр волокна (пс/км). Обычно поставщик не указывает эту цифру непосредственно, но ее легко вычислить по полосе пропускания. Например, полоса пропускания 400 МГц/км представляет максимальную модовую дисперсию, которую вы можете ожидать от волокна, 1/400 МГц/км, что равно 2,5 нс/км.
В разделе 8.3.2 описаны методики вычисления результатов модовой дисперсии в системе.
1.3. СВОЙСТВА СВЕТОВОДА, ОСНОВАННЫЕ НА ЗАКОНАХ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
1.3.1 Волновая трактовка световых процессов. Классы волн
Волны подразделяются на классы и типы.
На уровне электромагнитного взаимодействия с молекулами учитывается явление электрической поляризации, пространственные электрические E и магнитные H поля. Они допускают колебания соответствующих векторов (E, H) только в определённых плоскостях.
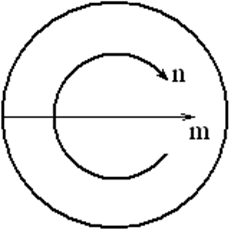
Волноведущую систему можно представить идеальным цилиндром с продольной осью z, а оси x и y образуют поперечную (xy), горизонтальную (xz) и вертикальную (yz) плоскости. В этой системе выделяют 4 класса волн по признаку отсутствия либо наличия продольных составляющих Ez и Hz (рисунок 1.7).
Следует обратить внимание на то, что термин «электрическая волна» не означает, что существует лишь электрическое поле и лишь вектор напряжённости электрического поля. В этой волне, как и во всех направляемых волнах, существует электромагнитное поле, т.е. обязательно электрический и магнитный векторы.
1.3.2 Типы волн (моды)
Рисунок 1.8 – Пояснение к понятию «тип волны»
Оказывается, что в ВС существуют только два типа волн HEnm и EHnm.
При n=0 имеем симметричные моды E0m и H0m.
При n≥1 имеем несимметричные (гибридные) моды HEnm и EHnm.
Часть внеапертурных лучей распространяется в оболочке, соответствующие им моды называют оболочечными. Они играют определённую роль в улучшении характеристик световодов. Чем меньше диаметр сердцевины dc, тем меньше сечение светового потока, поступающего в оптическое волокно, тем меньше различных типов колебаний (обусловленных множеством решений уравнений Максвелла), или мод, возникает в нём.
В ОМ волоконом световоде поддерживается только одна гибридная мода HE11, называемая основной модой. В ММ волоконном световоде поддерживаются различные, как гибридные моды так и Е- и Н- моды.
Не все моды указанных наборов можно реализовать. Чтобы понять, какие моды могут возникнуть, нужно провести достаточно сложный и кропотливый анализ. Сопоставляя волновую теорию с геометрической оптикой, следует отметить, что симметричные моды E0m и H0m соответствуют меридиональным лучам, несимметричные (смешанные) моды HEnm и EHnm – косым лучам.
1.3.3 Структура поля
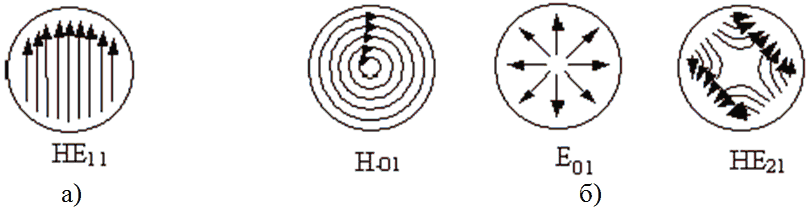
Как мы убедились, вдоль круглого неоднородного диэлектрического световода с осесимметричным распределением ε в сердцевине возможно распространение дискретного числа различных по структуре поля типов колебаний (мод) (рисунок 1.9).
а – мода самого низкого порядка; б – первый ряд мод более высоких порядков
Рисунок 1.9 – Картины векторов поперечного электрического поля в поперечном сечении сердцевины ступенчатого волоконного световода для четырёх мод самых низких порядков
Они отличаются кроме числа вариаций поля по азимуту и радиусу ещё и соотношением между продольными компонентами Ez и Hz.
1.3.4 Оптические параметры световода
Основными электродинамическими характеристиками регулярного световода при небольшом числе распространяющихся мод являются:
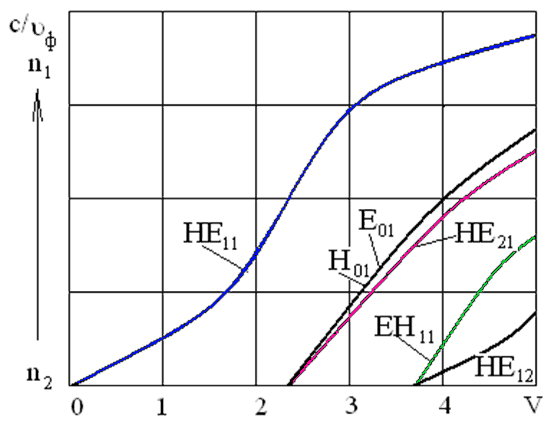
Рисунок 1.10 – Дисперсионные характеристики ступенчатого волоконного световода для нескольких первых мод
Эти дисперсионные характеристики начинаются при с/υф=n2.
С увеличением V; фазовые скорости уменьшаются, но всегда находятся в пределах:
Равенство с/υф=n2 представляет собой условие частоты отсечки Vотс.
Частота отсечки – предельная частота, ниже которой невозможно возникновение моды с определёнными индексами. Точки на оси абсцисс, в которых начинаются дисперсионные кривые, соответствуют критическим значениям нормированной частоты V.
Нормированную частоту отсечки Vотс также называют нормированной критической частотой Vkp. На частоте отсечки поле выходит из сердцевины в оболочку и мода исчезает.
Направляемую волну, имеющую наименьшую критическую частоту в данной среде распространения, называют основной волной.
В волоконном световоде для основной волны НЕ11 Vkp=0.
Для основной волны может быть реализован одноволновый или одномодовый режим в пределах от критической частоты основного типа до критической частоты волны ближайшего типа.
Если на заданной рабочей частоте параметры световода выбрать так, чтобы следующие высшие моды Е01, H01, HЕ21 с более высокими частотами отсечки не могли распространяться, то получим одномодовый световод, т.е. световод с одной только распространяющейся модой HЕ11. В этом случае должно выполняться условие одномодовости для двухслойного световода. Расчёт на основе уравнений Максвелла и рисунок 1.10 позволяют найти простой критерий распространения одной наинизшей моды:
| 0 2,405, то режим работы волоконного световода многомодовый. На этой стадии удобно перейти к рассмотрению ненормированных критических параметров. Для определения критической частоты и критической длины волны мод более высоких порядков можно воспользоваться следующими формулами: 1.3.5 Диаметр поля модыВвиду сложности точных решений поперечное поле моды (называемое также пятном моды) аппроксимируется гауссовской кривой вида
где rnm – фактический радиус поля (пятна) моды На практике размер, или диаметр, поля моды dпм определяется по ширине указанной гауссовской кривой распределения поперечного поля на уровне 1/e=0,368 от максимума. Он сравним с диаметром сердцевины dc в ОМ световоде из-за наличия экспоненциально спадающего поля моды за границами сердцевины. Производители приводят измеренное значение диаметра поля моды dпм в качестве нормируемого параметра ОМ световода, эквивалентного физическому диаметру сердцевины. Диаметр поля основной моды для типичного ОМ световода составляет dпм=12,7мкм на длине волны λ=1150нм и dпм=9,4мкм на длине волны λ=1230нм и сложно зависит от длины волны. 1.3.6 Число мод многомодового световодаЧисло мод, возникающих в ММ ВС со ступенчатым профилем показателя преломления, можно оценить, используя формулу: С помощь формулы (1.6) и (1.9) получим Значение этого выражения может быть как целым, так и дробным. В действительности число мод может быть только целым (от одной до нескольких тысяч). Поэтому расчётные значения N округляются в меньшую сторону. Число мод для градиентного световода с параболическим профилем показателя преломления сердцевины: Так, для широко используемого ММ световода с минимальным диаметром сердцевины dc=50мкм и числовой апертурой NA=0,20 при длине волны источника λ=1300нм, получаем N=292 для ступенчатого и N=146 для плавного профиля показателя преломления. При переходе к меньшим диаметрам сердцевины dc, меньшим разностям n1 и n2 и большим λ количество мод уменьшается. 1.2 СВОЙСТВА СВЕТОВОДА, ОСНОВАННЫЕ НА ЗАКОНАХ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ1.2.1 Виды световодовСветовод – это устройство, ограничивающее область распространения оптических колебаний и направляющее поток световой энергии в заданном направлении.
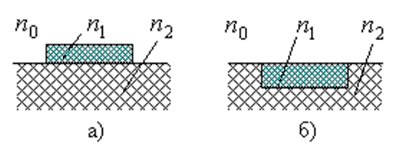
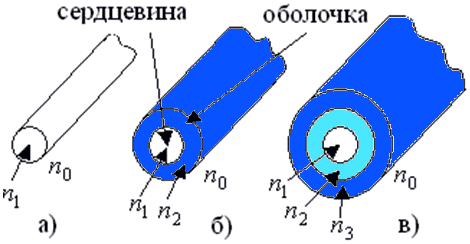
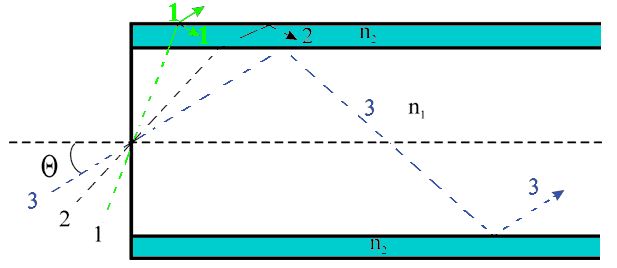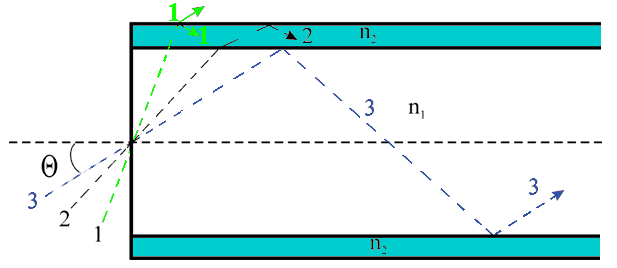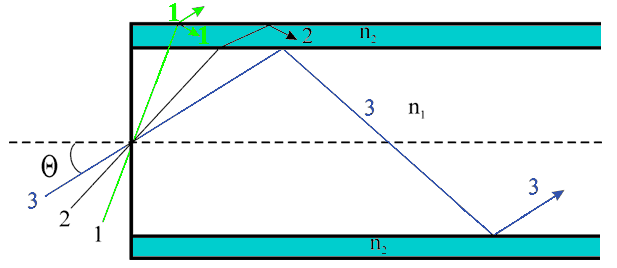
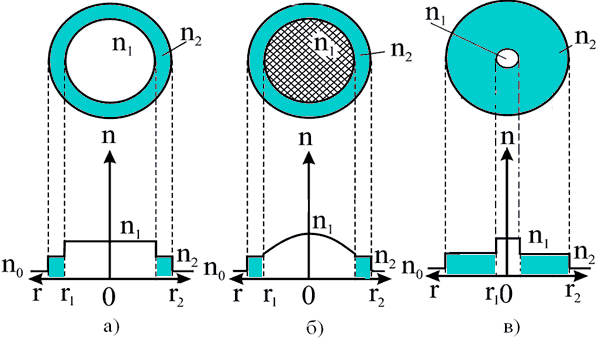
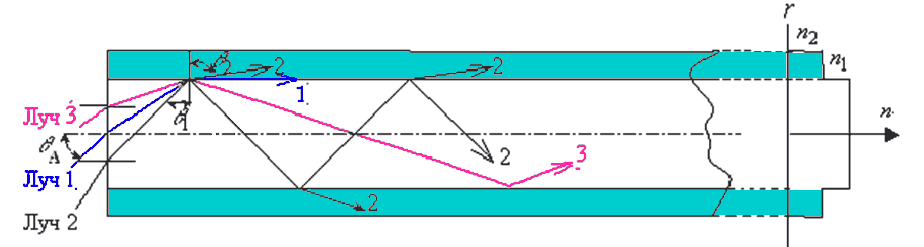
Плоские (планарные) световоды в свою очередь подразделяют на плёночные (рисунок 1.1,а) и канальные (рисунок 1.1,б). Волоконный световод (ВС) – это направляющая система, выполненная в виде тонкого стеклянного волокна цилиндрической формы, состоящая из сердцевины и оболочки, по которой осуществляется передача световых волн. Волоконные световоды бывают однослойные (рисунок 1.2,а), двухслойные (рисунок 1.2,б) и трёхслойные (рисунок 1.2,в) и т.д. Показатель преломления материала сердцевины n1= √┓, а оболочки – n2= √└, где ┓ и └ – относительные диэлектрические проницаемости. Относительная магнитная проницаемость материала μ обычно постоянна и равна единице. Показатель преломления вакуума n0 равен единице. Типичный волоконный световод представляет собой длинную нить диаметром от 100 до 1000мкм в зависимости от применений, состоящую из цилиндрической сердцевины, окружённой одной или несколькими оболочками из материалов с меньшими показателями преломления. Показатель преломления оболочки постоянен, а сердцевины в общем случае является функцией поперечной координаты (например, радиуса в случае круглого световода). Эту функцию называют профилем показателя преломления (ППП). Отрезки световодов используют для построения оптических устройств как активных (генераторов, модуляторов, демодуляторов и т.п.), так и пассивных (ответвителей, мостов, соединителей и т.п.). 1.2.2 Принцип действия волоконного световода. Типы лучей. МодыДля передачи электромагнитной энергии по световоду используется известное явление полного внутреннего отражения на границе раздела двух диэлектрических сред, поэтому, как будет показано ниже, необходимо, чтобы n1>n2. Разность показателей преломления на границе «сердцевина – оболочка» обычно составляет 1–0,1%. Кроме того, оболочка защищает распространяющийся по сердцевине свет от любых внешних воздействий и помех. В зависимости от величины угла θ, который образуют с осью лучи, выходящие из точечного источника в центре торца световода (рисунок 1.3), возникают лучи излучения 1, лучи оболочки 2 и лучи сердцевины 3.
Типы лучей. В сердцевине существуют два типа лучей: меридиональные, которые пересекаются в некоторой точке с осью световода и косые, которые с осью световода не пересекаются. На рисунке 1.3 показаны меридиональные лучи. Лучи, траектории которых полностью лежат в оптически более плотной среде, называются направляемыми. Поскольку энергия в направляемых лучах не рассеивается наружу, такие лучи могут распространяться на большие расстояния. Моды. Световые волны, которые образуются направляемыми лучами, многократно отражаясь от границы «сердцевина – оболочка», накладываются сами на себя и образуют направляемые волны (моды). Для облегчения восприятия под модой достаточно понимать вид траектории, вдоль которой распространяется свет. 1.2.3 Типы волокнаОптическое волокно – это сочетание стеклянного волокна с защитным покрытием, являющимся конструктивным элементом. Термин используется обычно при рассмотрении конструктивных и технологических особенностей волоконно оптических кабелей. Термины «оптическое волокно» и «волоконный световод» являются синонимами. Последний обычно применяется при рассмотрении вопросов передачи информации с помощью законов оптики. Волокно, в котором распространяется несколько мод, называется многомодовым (ММ). В ММ волокне диаметр сердцевины больше длины волны (dc>>λ). Волокно, в котором распространяется одна мода называется одномодовым (ОМ). В ОМ волокне диаметр сердцевины соизмерим с длиной волны (dc≈λ). По существующему международному стандарту для средств связи принято, что диаметр оболочки волокна должен быть равен 125 мкм. Оболочка изготавливается из кварцевого стекла (SiO2) с n2=1,45, а сердцевина – из кварцевого стекла с добавками GeO2 или P2O5. Для промышленно выпускаемых световодов ОМ волокно имеет диаметр сердцевины 7–10мкм, а ММ волокно – 50–65,5мкм.
Принцип передачи электромагнитной энергии по ступенчатому многомодовому, градиентному многомодовому и ступенчатому одномодовому волокну представлен на рисунке 1.5.
Лучи света входят в сердцевину волокна с торца и удерживаются за счёт полного внутреннего отражения внутри сердцевины (рисунок 1.5,а), или изгибаются в направлении градиента показателя преломления (рисунок 1.5, б). 1.2.4. Геометрические параметры световодаФормальные выкладки удобнее производить для ступенчатого световода, в котором показатель преломления сердцевины является постоянной величиной (n1=const). На рисунке 1.6 показан ход лучей в таком световоде.
где
Воспользуемся выражением n1sinθkp=n2 и выразим sinθA через показатель преломления сердцевины и оболочки, полагая n0=1: Для градиентного волокна используется понятие локальной числовой апертуры
значение которой максимально на оси и падает до 0 на границе сердцевины и оболочки. Для градиентного волокна с параболическим ППП используется понятие эффективной числовой апертуры:
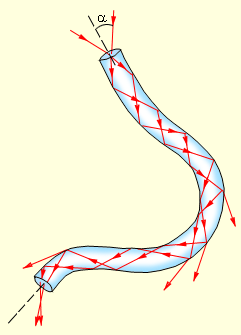
где n1(0) – максимальное значение показателя преломления. Нормированная частота. частотойОказывается целесообразным ввести нормированную частоту ν, которая объединяет структурные параметры ВС и длину волны излучения: Волновой анализ распространения света в волокнеЛекция 3 Распределение света по оптическому волокну 2. Электромагнитный подход; 3. Волновой анализ распространения света в волокне; 4. Распространение различных мод по оптоволокну; 5. Связь между понятиями луча и моды. Показатель преломления оболочки имеет постоянное значение, а показатель преломления сердцевины может оставаться постоянным или изменяться вдоль радиуса по определенному закону. Изменение показателей преломления ОВ вдоль радиуса называется профилем показателя преломления. Исходя из двойственной природы света, процесс распространения светового излучения в световодах можно изучать, используя методы геометрической оптики (лучевой подход) или волновые уравнения ЭМ поля (ЭМ подход). Лучевой подход Основная его идея заключается в том, что в оптическом диапазоне частот с достаточно большой точностью распространение волн можно представить как движение энергии волн по лучам, описываемым с помощью геометрических соотношений. Анализ распространения света в лучевом приближении составляет предмет геометрической оптики. Необходимым условием распространения света в ОВ в рамках лучевого подхода является требование падения лучей на торец ОВ в пределах входной угловой апертуры. Однако это условие не является достаточным, так как только часть из этих лучей будут распространяться вдоль оси световода. Лучевой подход основан на представлении источника излучения и светового луча соответственно в виде точки и линии (рисунок 3.1). S – точечный источник света Лучевой подход наглядно показывает процессы распространения света по световодам, однако им можно пользоваться только при соблюдении условия малости длины волны по сравнению с радиусом сердцевины волокна. Поэтому лучевой моделью можно пользоваться при изучении распространения света в многомодовых волокнах, где указанное условие соблюдается. Свет, попадающий на торец световода, может распространяться по нему на большие расстояния за счет полного внутреннего отражения от боковых поверхностей (рисунок 3.2). Научно-техническое направление, занимающееся разработкой и применением оптических световодов, называется волоконной оптикой. При сильном изгибе волокна закон полного внутреннего отражения нарушается, и свет частично выходит из волокна через боковую поверхность Напомним основные законы геометрической оптики: 1. Отражение света. Когда свет падает на границу раздела двух сред, определённая его часть отражается. Количество отражённого света зависит от угла α1 между падающим лучом света и нормалью к поверхности падения. Термин «луч света» здесь используется для обозначения пути, по которому проходит световая энергия. Для отражённого луча и угла α2, образованного нормалью к поверхности падения и отражённым лучом света (рисунок 3.3), имеют силу следующие утверждения: — остаётся в плоскости падения, образуемой падающим лучом света и нормалью к поверхности падения луча; — по отношению к падающему лучу света лежит на противоположной стороне от нормали к поверхности падения луча; — имеет угол отражения по отношению к нормали к поверхности падения, равный углу падения. 2. Преломление света. Когда луч света входит под углом падения α в оптически более плотную среду (например, стекло или воду) из оптически менее плотной среды (например, воздуха), то его направление распространения по отношению к нормали к поверхности падения изменяется, он преломляется под углом преломления β. Для изотропной среды, то есть материала или вещества, имеющего одинаковые свойства во всех направлениях, применим закон преломления Снеллиуса (1621г.): отношение угла падения к синусу угла преломления является величиной постоянной и также идентично отношению с1/с2 скоростей света с1 в первой среде и с2 во второй среде (рисунок 3.4) где α – угол падения; с1 – скорость света 1; β – угол преломления; с2 – скорость света 2. Рисунок 3.3 – Отражение света Рисунок 3.4 – Преломление света Из двух оптических сред более плотной называется та, в которой скорость света меньше. При переходе из вакуума (воздуха), где свет распространяется со скоростью со, в среду со скоростью света с имеет силу отношение Отношение скорости света со в вакууме к скорости света с в среде называется показателем преломления n (более точно, фазовым показателем преломления) соответствующей среды. Показатель преломления вакуума (воздуха) no=1. Для двух различных сред с показателями преломления n1 и n2 и скоростями света в них c1 и c2 имеют силу следующие соотношения: 3. Полное внутреннее отражение. Если луч света (3) падает на поверхность раздела между средой с показателем преломления n1 и средой с показателем преломления n2 о (рисунок 3.5). Рисунок 3.5 – Полное внутреннее отражение: 1′ – полностью отраженный луч света; 2′ – преломленный луч света с углом преломления β0=90; 3′ – преломленный луч света В этом случае луч света (2′) распространяется параллельно поверхности раздела двух сред. Угол падения sin то есть критический угол зависит от отношения показателей преломления n1 и n2 двух сред. Например, для критического угла между водой с n1=1,333 и воздухом с no=1 имеем sin Полное внутреннее отражение может происходить на поверхности раздела сред только тогда, когда луч света распространяется из оптически более плотной среды (например, стекло n1=1,5) в оптически менее плотную среду (например, воздух no=1), и никогда не происходит в обратном случае. У реальных ОВ, вследствие малой разности показателей преломления сердцевины п1 и оболочки п2, луч света проникает, а следовательно и распространяется по оболочке ОВ даже при углах падения φi > φпр, см. рисунок 3.6. Глубина проникновения волн в оболочку уменьшается при увеличении угла падения, при этом отраженная волна приобретает фазовый сдвиг, зависящий от угла падения. Глубина проникновения (δ), т.е. расстояние, на котором плоская волна ослабевает в е = 2,71 раза при φi > φпр определяется выражение: где λ — длина волны. Полное внутреннее отражение плоской волны на границе раздела двух сред сопровождается теми же эффектами, что и отражение от металлической плоскости, смещенной на некоторое расстояние λ0 от поверхности раздела. Поток энергии из первой среды во вторую в среднем равен нулю, поэтому энергия падающей ЭМ волны полностью возвращается в первую среду при условии отсутствия потерь энергии во второй среде. Электромагнитный подход Для расчета ЭМ процессов в световодах используют ряд математических моделей, отличающихся друг от друга сложностью математического аппарата и наглядностью. В первую очередь стремятся использовать наиболее простые в математическом плане модели, обладающие наибольшей наглядностью. При необходимости учета более сложных деталей процесса распространения света в световоде переходят к использованию более сложных математических моделей. В случае одномодовых волокон требуется ЭМ подход, т.е. решение волновых уравнений при заданных граничных условиях. Электромагнитный подход позволяет точно рассчитать число мод (лучей), которые могут распространяться по световоду. Расчет подразумевает совместное решение волновых уравнений для сердцевины и оболочки оптического волокна с учетом граничных условий. Для того, чтобы не делать расчет для каждого световода отдельно, а получить характеристики, присущие определенному типу световодов (например, для ступенчатого профиля), вводят понятие нормированной (характеристической) частоты. Нормированная частота является обобщенной характеристикой световода, поскольку зависит не только от геометрических и оптических характеристик световода, но и от длины волны источника излучения. Типы и число направляемых волн (мод).Для правильной эксплуатации волоконных световодов, а также нормирования разброса длин волн лазерных источников излучения, необходимо знать наименьшую эксплуатационную длину волны, называемую критической длиной волны волоконного световода, при которой может распространяться только одна фундаментальная мода. Один и тот же световод для длин волн, выше критической длины волны, работает в одномодовом режиме, а для длин волн ниже критической длины волны работает в многомодовом режиме. При лучевом подходе каждой из этих мод соответствует меридиональный луч с определенным углом наклона к оси волокна. Важным параметром любой моды является ее частота отсечки (f кр mn), называемая также критической частотой, ниже которой поле не распространяется вдоль световода. В случае симметричных мод для определения частот отсечки можно воспользоваться уравнением которое имеет бесчисленное множество решений (корней). Достоинством одномодовой передачи является широкая полоса передаваемых частот (несколько гигагерц) и меньшее затухание по сравнению с многомодовой. С увеличением числа мод полоса передаваемых частот сужается. Однако одномодовый режим требует применения когерентных источников излучения (лазеров). Для многомодовых систем передачи можно использовать простейшие источники излучения — светодиоды. Число мод (N) при ступенчатом профиле показателя преломления приблизительно равно Из выражения (3.8) видно, что значение V может быть уменьшено за счет уменьшения диаметра сердцевины и разности показателей преломления и увеличения рабочей длины волны. Число направляемых мод градиентного волокна равно При одинаковой нормированной частоте число направляемых мод градиентного ОВ в 2 раза меньше, чем у ступенчатого, что существенно улучшает его характеристики передачи. Когда нормированная частота при ступенчатом профиле световода меньше критического значения Vc= 2,405, волокно поддерживает распространение только одной фундаментальной моды. Волокно, в котором может распространяться только фундаментальная мода, называется одномодовым. Вследствие поляризации света фундаментальная мода может существовать в двух ортогональных поляризациях. Влияние поляризации необходимо учитывать при скорости передачи 2,5 Гбит/с и выше. Волновой анализ распространения света в волокне Количественный анализ ЭМ процессов проводится на основе уравнений Максвелла. Волновые уравнения получаются из уравнений Максвелла и характеризуют закон изменения векторов напряженности электрического и магнитного поля для гармонических процессов. Простейшим случаем волнового процесса является плоская волна. Плоской называют такую волну, при которой в ЭМ поле можно провести ряд параллельных плоскостей, перпендикулярных направлению распространения волны так, чтобы вектора Е и Н — общепринятое обозначение соответственно векторов электрического и магнитного поля — лежали в этих плоскостях и сохраняли как свое значение, так и направление вдоль всей плоскости. Так как волновые уравнения линейны, то общее решение уравнения является суперпозицией всех плоских волн, распространяющихся в любых направлениях. Понятие плоской волны при изучении ЭМ волн имеет такое же фундаментальное значение, как и гармонических (синусоидальных) колебаний при изучении изменяющихся во времени сложных процессов. Рассмотрим волновые процессы в идеальном ОВ двухслойной конструкции (см.рисунок 3.7)без потерь. Рисунок 3.7 – Волновые процессы в идеальном оптическом волокне Фазовая постоянная распространения плоских волн β1 в среде с показателем преломления п1 определяется в случае однородного диэлектрика соотношением Для рассмотрения процессов в оболочке (r где β2 = 2πn2/λ — фазовая постоянная распространения плоских волн в среде с диэлектрической проницаемостью, равной ε2, и соответственным показателем преломления п2 = Уравнения (3.10) и (3.11) однотипны, поэтому поясним подход к их решению на примере уравнения (3.10) для продольных составляющих Ez. В соотношениях между цилиндрическими функциями, с одной стороны, и показательной и тригонометрической функциями с другой имеется некоторая аналогия. Известные соотношения между последними Выбор вида цилиндрических функций, описывающих электромагнитное поле в сердцевине и оболочке, определяется физическими соображениями передачи направляемых мод и предельными значениями цилиндрических функций. |



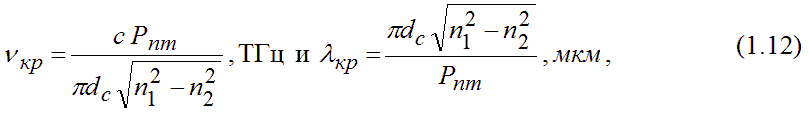
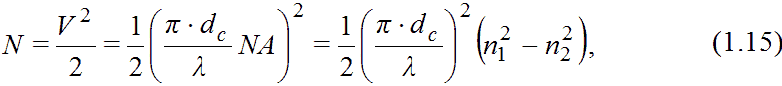
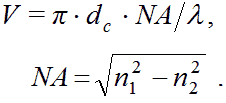
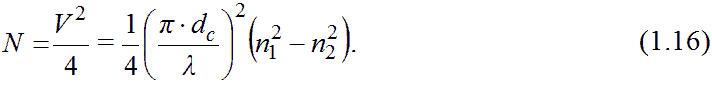


 ,(3.2)
,(3.2)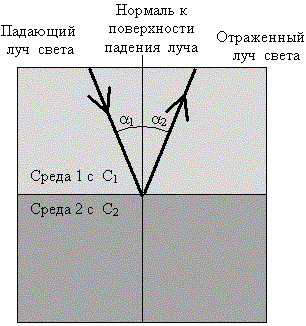

 . (3.3)
. (3.3) . (3.5)
. (3.5)
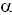 о называется критическим (предельным) углом двух сред. Для критического угла
о называется критическим (предельным) углом двух сред. Для критического угла  0,75 и
0,75 и  (3.6)
(3.6)
 . (3.7)
. (3.7) . (3.8)
. (3.8) . (3.9)
. (3.9)
 .
. а) воспользуемся теми же уравнениями (3.10) и (3.11) с заменой g1 на g2.
а) воспользуемся теми же уравнениями (3.10) и (3.11) с заменой g1 на g2.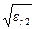 .
. ; (3.14)
; (3.14) (3.15)
(3.15)  ; (3.16)
; (3.16) . (3.17)
. (3.17)