чем описывается состояние микрочастицы в квантовой механике

Определение состояния микрочастицы в квантовой механике. Волновая функция

Для классической частицы ее состояние в любой момент вре­мени задается координатой частицы x(t) и ее скоростью v(t) = dx/dt (в простейшем случае одномерного движения вдоль оси X). Такое определение состояния в квантовой механике не имеет никакого смысла из-за соотношения неопределенностей.

Данная ситуация связана с наличием у микрочастиц волновых свойств. В частности, одинаковые дифракционные картины при распространении волн и движении микрочастиц позволяют допустить, что и поведение микрочастиц описывается неким волновым уравнением.

Разложение волновой функции в ряд Фурье дает все возможные результаты измерения импульса частицы. Вероятность каж­дого из этих результатов определяется квадратом соответствующе­го коэффициента разложения Фурье. При этом каждое новое измерение координат и импульса частицы изменяет существовавшее до него распределение вероятностей.

Уравнение Шредингера

По определению квантового состояния уравнение движения квантовой частицы должно задавать изменения во времени вол­новой функции ψ. Такое уравнение впервые было предложено Э.Шредингером в 1926 г, и названо его именем. Обратим внимание на то, что уравнение Шредингера (как и уравнение Ньютона) не выводится, а постулируется. В простом случае, когда ψ-функция не зависит от времени, уравнение называется стационарным и имеет следующий вид:

— оператор Лапласа (лапласиан).

В общее (или временное) уравнение Шредингера входит также производная dψ/dt, отражающая изменение волновой функции времени.

Источник

Квантовая механика

Слово «квант» происходит от латинского quantum («сколько, как много») и английского quantum («количество, порция, квант»). «Механикой» издавна принято называть науку о движении материи. Соответственно, термин «квантовая механика» означает науку о движении материи порциями (или, выражаясь современным научным языком науку о движении квантующейся материи). Термин «квант» ввел в обиход немецкий физик Макс Планк (см. Постоянная Планка) для описания взаимодействия света с атомами.

Квантовая механика часто противоречит нашим понятиям о здравом смысле. А всё потому, что здравый смысл подсказывает нам вещи, которые берутся из повседневного опыта, а в своем повседневном опыте нам приходится иметь дело только с крупными объектами и явлениями макромира, а на атомарном и субатомном уровне материальные частицы ведут себя совсем иначе. Принцип неопределенности Гейзенберга как раз и очерчивает смысл этих различий. В макромире мы можем достоверно и однозначно определить местонахождение (пространственные координаты) любого объекта (например, этой книги). Не важно, используем ли мы линейку, радар, сонар, фотометрию или любой другой метод измерения, результаты замеров будут объективными и не зависящими от положения книги (конечно, при условии вашей аккуратности в процессе замера). То есть некоторая неопределенность и неточность возможны — но лишь в силу ограниченных возможностей измерительных приборов и погрешностей наблюдения. Чтобы получить более точные и достоверные результаты, нам достаточно взять более точный измерительный прибор и постараться воспользоваться им без ошибок.

Теперь если вместо координат книги нам нужно измерить координаты микрочастицы, например электрона, то мы уже не можем пренебречь взаимодействиями между измерительным прибором и объектом измерения. Сила воздействия линейки или другого измерительного прибора на книгу пренебрежимо мала и не сказывается на результатах измерений, но чтобы измерить пространственные координаты электрона, нам нужно запустить в его направлении фотон, другой электрон или другую элементарную частицу сопоставимых с измеряемым электроном энергий и замерить ее отклонение. Но при этом сам электрон, являющийся объектом измерения, в результате взаимодействия с этой частицей изменит свое положение в пространстве. Таким образом, сам акт замера приводит к изменению положения измеряемого объекта, и неточность измерения обусловливается самим фактом проведения измерения, а не степенью точности используемого измерительного прибора. Вот с какой ситуацией мы вынуждены мириться в микромире. Измерение невозможно без взаимодействия, а взаимодействие — без воздействия на измеряемый объект и, как следствие, искажения результатов измерения.

О результатах этого взаимодействия можно утверждать лишь одно:

неопределенность пространственных координат × неопределенность скорости частицы > h/m,

или, говоря математическим языком:

где Δx и Δv — неопределенность пространственного положения и скорости частицы соответственно, h — постоянная Планка, а m — масса частицы.

Соответственно, неопределенность возникает при определении пространственных координат не только электрона, но и любой субатомной частицы, да и не только координат, но и других свойств частиц — таких как скорость. Аналогичным образом определяется и погрешность измерения любой такой пары взаимно увязанных характеристик частиц (пример другой пары — энергия, излучаемая электроном, и отрезок времени, за который она испускается). То есть если нам, например, удалось с высокой точностью измерили пространственное положение электрона, значит мы в этот же момент времени имеем лишь самое смутное представление о его скорости, и наоборот. Естественно, при реальных измерениях до этих двух крайностей не доходит, и ситуация всегда находится где-то посередине. То есть если нам удалось, например, измерить положение электрона с точностью до 10 –6 м, значит мы одновременно можем измерить его скорость, в лучшем случае, с точностью до 650 м/с.

Из-за принципа неопределенности описание объектов квантового микромира носит иной характер, нежели привычное описание объектов ньютоновского макромира. Вместо пространственных координат и скорости, которыми мы привыкли описывать механическое движение, например шара по бильярдному столу, в квантовой механике объекты описываются так называемой волновой функцией. Гребень «волны» соответствует максимальной вероятности нахождения частицы в пространстве в момент измерения. Движение такой волны описывается уравнением Шрёдингера, которое и говорит нам о том, как изменяется со временем состояние квантовой системы.

Картина квантовых событий в микромире, рисуемая уравнением Шрёдингера, такова, что частицы уподобляются отдельным приливным волнам, распространяющимся по поверхности океана-пространства. Со временем гребень волны (соответствующий пику вероятности нахождения частицы, например электрона, в пространстве) перемещается в пространстве в соответствии с волновой функцией, являющейся решением этого дифференциального уравнения. Соответственно, то, что нам традиционно представляется частицей, на квантовом уровне проявляет ряд характеристик, свойственных волнам.

Согласование волновых и корпускулярных свойств объектов микромира (см. Соотношение де Бройля) стало возможным после того, как физики условились считать объекты квантового мира не частицами и не волнами, а чем-то промежуточным и обладающим как волновыми, так и корпускулярными свойствами; в ньютоновской механике аналогов таким объектам нет. Хотя и при таком решении парадоксов в квантовой механике всё равно хватает (см. Теорема Белла), лучшей модели для описания процессов, происходящих в микромире, никто до сих пор не предложил.

Источник

Квантовая система

Вы будете перенаправлены на Автор24

Квантовая система

Для объяснения многих свойств микрочастиц (фотонов, электронов и др.) требуются специальные законы и подходы квантовой механики. Квантовые свойства микромира проявляются через свойства макросистем. Микрообъекты составляют определенную физическую систему, которая называется квантовой. Примерами квантовых систем могут служить: фотонный газ, электроны в металлах. Под терминами квантовая система, квантовая частица следует понимать материальный объект, который описывается с помощью специального аппарата квантовой механики.

Квантовая механика исследует свойства и явления мира микрочастиц, которые не может трактовать классическая механика. Такими особенностями, например, стали: корпускулярно-волновой дуализм, дискретность, существование спинов. Методы классической механики не могут описать поведение частиц микромира. Имеющиеся одновременно волновые и корпускулярные свойства у микрочастицы не дают возможности определить состояние частицы с классической точки зрения.

Данный факт отразился в соотношении неопределенности Гейзенберга ($1925г.$):

Имея корпускулярные и одновременно волновые свойства, микрочастица не обладает точной координатой, а является «размазанной» в некоторой области пространства. В случае присутствия в некоторой области пространства двух и более частиц не возможно их отличить друг от друга, так как нельзя отследить за движением каждой. Из вышесказанного следует тождественность частиц в квантовой механике.

Готовые работы на аналогичную тему

Некоторые параметры, относящиеся к микрочастицам, принимают дискретные значения, что классическая механика объяснить не может. В соответствии с положениями и законами квантовой механики, помимо энергии системы, дискретными могут быть момент количества движения системы:

спин может принимать значения:

Проекция магнитного момента на направление внешнего поля принимает значения:

С целью математического описания квантовых особенностей физических величин в соответствие каждой величине ставят оператор. Так, в квантовой механике физические величины отображаются операторами, при этом их значения определяются средними по собственным значениям операторов.

Состояние квантовой системы

Любое состояние в квантовой системе описывается при помощи волновой функции. Однако данная функция прогнозирует параметры будущего состояния системы с некоторой долей вероятности, а не достоверно, то является принципиальным отличием от классической механики. Таким образом, для параметров системы волновая функция определяет вероятностные значения. Такая неопределенность, неточность предсказаний более всего вызывала споры в среде ученых.

Измеряемые параметры квантовой системы

Самые глобальные различия между классической и квантовой механикой заключены в роли измерения параметров изучаемой квантовой системы. Проблема измерений в квантовой механике заключается в том, что при попытках провести измерения параметров микросистемы исследователь действует на систему макроприбором, чем изменяет состояние самой квантовой системы. Так, при попытке точно измерить параметр микрообъекта (координату, импульс, энергию), мы сталкиваемся с тем, что сам процесс измерения изменяет параметры, которые мы пытаемся измерить, причем существенно. Провести точные измерения в микромире невозможно. Всегда будет иметь место ошибки в соответствии с принципом неопределенности.

В квантовой механике динамические переменные представляют операторы, поэтому говорить о числовых значениях не имеет смысла, так как оператор определяет действие на вектор состояния. Результат представлен, так же вектором пространства Гильберта, а не числом.

В том случае, если вектор состояния не собственный вектор оператора динамической переменной, то результат измерения не становится однозначным и говорят только о вероятности того или иного значения получаемого в измерении.

Результатами теории, которые проверяемы эмпирически служат вероятности получения в измерении динамической переменной при большом количестве измерений для одного и того же вектора состояния.

Процессы, которые происходят в микромире лежат за пределами чувственного восприятия человека. Следовательно, понятия и явления, которые использует квантовая механика, лишены наглядности.

Решение:

В качестве основы для решения задачи используем соотношение неопределенностей Гейзенберга в виде:

\[\triangle p_x\triangle x\ge \hbar \left(1.1\right),\]

\[\triangle p_x=m\triangle v_x\left(1.2\right).\]

Подставим правую часть выражения (1.2) вместо неопределенности проекции импульса в выражении (1.1), имеем:

\[m\triangle v_x\triangle x\ge \hbar \left(1.3\right).\]

Из формулы (1.3) выразим искомую неопределенность скорости:

Из неравенства (1.4) следует, что минимальная погрешность при определении скорости частицы равна:

Задание: Какова минимальная погрешность в измерении кинетической энергии электрона, если он находится в области, размер которой l.

Решение:

В качестве основы для решения задачи используем соотношение неопределенностей Гейзенберга в виде:

\[\triangle p_xl\ge \hbar \to \triangle p_x\ge \frac<\hbar >\left(2.1\right).\]

Из неравенства (2.1) следует, что минимальная погрешность импульса равна:

Погрешность кинетической энергии можно выразить как:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 06 05 2021

Источник

Чем описывается состояние микрочастицы в квантовой механике

В результате углубления знаний о природе света выяснилось, что в оптических явлениях обнаруживается своеобразный дуализм. Наряду с такими свойствами света, которые самым непосредственным образом свидетельствуют о его волновой природе (интерференция, дифракция), имеются и другие свойства, столь же непосредственно обнаруживающие его корпускулярную природу (фотоэффект, явление Комптона).

В 1924 г. Луи де Бройль выдвинул смелую гипотезу, что дуализм не является особенностью одних только оптических явлений, но имеет универсальное значение. Фотон, как известно, обладает энергией и импульсом . По идее де Бройля, движение электрона или какой-либо другой частицы связано с волновым процессом, длина волны которого равна , а частота . Гипотеза де Бройля вскоре была блестяще подтверждена экспериментально. Дэвиссон и Джермер обнаружили, что пучок электронов, рассеивающийся от кристаллической пластинки, дает дифракционную картину. Томсон и независимо от него Тартаковский получили дифракционную картину при прохождении электронного пучка через металлическую фольгу. Штерн и его сотрудники показали, что дифракционные явления обнаруживаются также у атомных и молекулярных пучков. Во всех перечисленных случаях дифракционная картина соответствует длине волны, определяемой соотношением .

Обнаружение волновых свойств микрочастиц свидетельствовало о том, что классическая механика не может дать правильного описания поведения подобных частиц. Возникла необходимость создать механику микрочастиц, которая учитывала бы также и их волновые свойства. Новая механика, созданная Шредингером, Гейзенбергом, Дираком и другими, получила название волновой или квантовой механики. Основным уравнением квантовой механики является уравнение Шредингера (это уравнение было установлено в 1926 г.). Состояние микрочастицы описывается в квантовой механике так называемой волновой функцией, которую принято обозначать буквой Ψ.

Физический смысл функции Ψ заключается в том, что квадрат её модуля дает плотность вероятности (вероятность, отнесенную к единице объема) нахождения частицы в соответствующем месте пространства. Из сказанного вытекает, что квантовая механика имеет статистический характер. Она не позволяет определить местонахождение частицы в пространстве или траекторию, по которой движется частица. С помощью волновой функции можно лишь предсказать, с какой вероятностью частица может быть обнаружена в различных точках пространства.

На первый взгляд может показаться, что квантовая механика дает значительно менее точное и исчерпывающее описание движения частицы, чем классическая механика, которая определяет «точно» местоположение и скорость частицы в каждый момент времени. Однако в действительности это не так. Квантовая механика гораздо глубже вскрывает истинное поведение микрочастиц. В применении к микрочастицам понятия определенного местоположения и траектории вообще теряют смысл. Движение по определенной траектории несовместимо с волновыми свойствами, что становится совершенно очевидным, если проанализировать существо опытов по дифракции.

Степень точности, с какой к частице может быть применено представление об определенном положении ее в пространстве, дается соотношением неопределенностей, установленным Гейзенбергом. Согласно этому соотношению частица не может иметь одновременно вполне точные значения, например, координаты x и соответствующей этой координате составляющей импульса p_x, причем неопределенности в значениях этих величин удовлетворяют условию: . Такая запись означает, что произведение неопределенностей координаты и соответствующего ей импульса не может быть меньше величины порядка . Чем точнее определена одна из величин, x или p_x тем больше становится неопределенность другой. Возможны состояния частицы, при которых одна из величин имеет вполне точное значение, но тогда вторая величина будет совершенно неопределенной.

Соотношение неопределенностей отражает двойственную корпускулярно-волновую природу микрочастиц. Одного этого соотношения достаточно, чтобы получить ряд важных результатов. В частности, оно позволяет объяснить тот факт, что электрон не падает на ядро атома. Если бы электрон упал на точечное ядро, его координаты и импульс приняли бы определенные (нулевые) значения, что несовместимо с принципом неопределенности. Также принцип позволяет оценить размеры простейшего атома и минимальную возможную энергию электрона в таком атоме: , . Полученные значения совпадают с радиусом и энергией первой боровской орбиты водородного атома.

Источник

Основные положения квантовой механики. Особенности поведения микрочастиц. Волновая функция. Принцип суперпозиции состояний

Страницы работы

Содержание работы

ЛЕКЦИИ ПО КВАНТОВОЙ МЕХАНИКЕ

ГЛАВА 1. ОСНОВНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ МЕХАНИКИ

особенности поведения микрочастиц,

принцип суперпозиции состояний.

полный набор наблюдаемых

спектр собственных значений

принцип суперпозиции состояний

Особенности поведения микрочастиц.

Впервые гипотеза о наличии у частиц волновых свойств была высказана Луи де-Бройлем. В соответствии с гипотезой де-Бройля каждой частице можно сопоставить плоскую монохроматическую волну 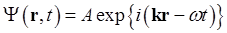, волновой вектор и частота которой связаны с импульсом и энергией частицы соотношениями: Е=ħω, Р=ħk. Вскоре эта гипотеза получила блестящее подтверждение в опытах Дэвиссона и Джермера, в которых наблюдалась дифракция электронов рассеянных кристаллами никеля, а затем и в экспериментах с другими частицами (нейтронами, атомами, молекулами и т.п.). Появление дифракционных максимумов и минимумов при рассеянии под разными углами можно объяснить по аналогии с классическими волнами интерференцией волн де-Бройля, рассеянных разными элементами кристаллической решётки и, имеющих вследствие этого сдвиг по фазе. При этом в отличие от классических волн, квадрат модуля амплитуды которых описывает распределение интенсивности, квадрат модуля амплитуды волн де-Бройля описывает распределение вероятности попадания частицы в некоторую точку пространства.

Описанное выше поведение микрочастиц несовместимо с представлением об их движении по траекториии, для построения которой необходимо в каждый момент времени точно знать координату и скорость (или импульс) частицы. Таким образом, мы приходим к одному из основополагающих принципов квантовой механики – принципу неопределённости. Согласно принципу неопределённости частица не может одновременно иметь вполне определённые, точные значения координаты и импульса. Все остальные динамические переменные классической механики можно представить как функции координат и импульсов. Поэтому и другие пары динамических переменных, или, как принято их называть в квантовой механике, наблюдаемых могут не иметь в одно и то же время определённых значений.

Совокупность максимального числа независимых наблюдаемых, которые могут одновременно иметь определённые значения, называется полным набором наблюдаемых.

Как следует из сказанного выше, в общем случае наблюдаемая не имеет строго определённого значения. Это означает, что при измерении с той или иной вероятностью можно получить разные значения наблюдаемой. Такой вероятностный характер поведения является характерной особенностью микрочастиц. В качестве иллюстрации к сказанному рассмотрим пример, в котором пучок линейно поляризованного монохроматического света интенсивностью I₀ падает нормально на поверхность поляризующей плёнки, плоскость поляризации которой составляет угол φ с плоскостью поляризации падающего света. Интенсивность прошедшего света I определяется законом Малюса: I=I₀ cos 2 φ. Обсудим это пример, рассматривая падающий свет, как совокупность фотонов, имеющих в данном случае одинаковые характеристики (частоту, волновой вектор и направление поляризации). Прошедшие через плёнку фотоны характеризуются той же частотой и волновым вектором, что и падающие на поверхность плёнки. Уменьшение интенсивности света при прохождении плёнки можно объяснить только тем, что через неё смогли пройти не все фотоны. Но в падающем пучке все фотоны были одинаковы. Поэтому следует допустить, что каждый фотон имеет некоторую вероятность пройти или быть задержанным поляризующей плёнкой. Вероятность прохождения фотона через плёнку составляет как раз величину равную cos 2 φ. Плоскость поляризации прошедшего через плёнку света, как известно, совпадает с плоскостью поляризации плёнки вне зависимости от того, каким было первоначальное направление его поляризации. Это обстоятельство говорит о том, что процесс измерения может тем или иным образом, в зависимости от типа измерения менять исходное состояние частицы. Под процессом измерения здесь и далее мы будем понимать любое воздействие на объект, в результате которого определяется одна или несколько его динамических характеристик.

Ещё одной особенностью поведения микрочастиц является то обстоятельство, что некоторые динамические переменные, характеризующие их движение, могут принимать лишь строго определённые дискретные значения. К таким динамическим переменным, как следует из экспериментов по расщеплению пучков частиц в магнитном поле, относится, например, механический (и связанный с ним магнитный) момент. Дискретные значения принимают и значения энергии электронов, находящихся в атомах в связанном состоянии, о чём, в частности, свидетельствует линейчатый характер их оптического спектра. К такому же выводу приводят результаты знаменитых опытов Франка и Герца по рассеянию электронов на атомах ртути.

Совокупность значений, которые может принимать та или иная наблюдаемая, называется спектром собственных значений этой наблюдаемой.

Источник