чем обусловлено сопротивление металлов

Электрический ток в металлах

Электрическим током в металлах называют упорядоченное движение электронов под действием электрического поля.

Исходя из опытов, видно, что металлический проводник вещество не переносит, то есть ионы металла не участвуют в передвижении электрического заряда.

Носители тока в металлах

При исследованиях были получены доказательства электронной природы тока в металлах. Еще в 1913 году Л.И. Мандельштам и Н.Д. Папалекси выдали первые качественные результаты. А в 1916 году Р. Толмен и Б. Стюарт модернизировали имеющуюся методику и выполнили количественные измерения, которые доказывали, что движение электронов происходит под действием тока в металлических проводниках.

Данная формула объясняет, что l – это мгновенное значение силы тока в катушке, R – полное сопротивление цепи, υ 0 – начальная линейная скорость проволоки. Видно, что определение удельного заряда e m в металлах производится, исходя из формулы:

Величины, находящиеся с правой стороны, можно измерить. Основываясь на результатах опытов Толмена и Стюарта, установили, что носители свободного заряда имеют отрицательный знак, а отношение носителя в его массе близко по значению удельного заряда электрона, получаемого в других опытах. Было выявлено, что электроны – это носители свободных зарядов.

Потенциальный барьер. Движение электронов в кристаллической решетке

После взаимодействия электронов с ионами первые покидают металл, преодолевая только потенциальный барьер.

Высота такого барьера получила название работы выхода.

Наличие комнатной температуры не позволяет электронам проходить этот барьер. Потенциальная энергия выхода электрона после взаимодействия с кристаллической решеткой намного меньше, чем при удалении электрона из проводника.

Расположение е в проводнике характеризуется наличием потенциальной ямы, глубина которой получила название потенциального барьера.

Ионы, образующие решетку, и электроны принимают участие в тепловом движении. Благодаря тепловым колебаниям ионов вблизи положений равновесий и хаотичному движению свободных электронов, при столкновении первых со вторыми происходит усиление термодинамического равновесия между электронами и решеткой.

По теории Друде-Лоренца имеем, что электроны имеют такую же среднюю энергию теплового движения, как и молекулы одноатомного идеального газа. Это делает возможным оценивание средней скорости υ т ¯ теплового движения электронов, используя молекулярно-кинетическую теорию.

Классическая электронная теория металлов предполагает, что их движение подчинено законам механики Ньютона. Данная теория характеризуется тем, что происходит пренебрежение взаимодействием электронов между собой, а взаимодействие с положительными ионами расценивается как соударения, при каждом из которых e сообщает накопленную энергию решетке. Поэтому принято считать, что после соударения движение электрона характеризуется нулевой дрейфовой скоростью.

Абсолютно все выше предложенные допущения приближенные. Это дает возможность объяснения законов электрического тока в металлических проводниках, основываясь на электронной классической теории.

Закон Ома

Конец свободного пробега характеризуется дрейфовой скоростью электрона, которую определяют по формуле

U = E l – это напряжение на концах проводника. Формула выражает закон Ома для металлического проводника. Тогда электрическое сопротивление необходимо находить:

Удельное сопротивление ρ и удельная проводимость ν выражаются как:

Закон Джоуля-Ленца

Конец пробега электронов под действием поля характеризуется кинетической энергией

Исходя из предположений, энергия при соударениях передается решетке, а в последствии переходит в тепло.

Время ∆ t каждого электрона испытывается ∆ t τ соударений. Проводник с сечение S и длиной l имеет n S l электронов. Тогда выделившееся тепло в проводнике за ∆ t равняется

Данное соотношение выражает закон Джоуля-Ленца.

Благодаря классической теории, имеет место трактовка существования электрического сопротивления металлов, то есть законы Ома и Джоуля-Ленца. Классическая электронная теория не в состоянии ответить на все вопросы.

Классическая электронная теория не объясняет температурную зависимость удельного сопротивления металлов. По теории ρ

Сопротивление металлического проводника

Особый интерес представило явление сверхпроводимости. В 1911 году его открыл Х. Каммерлинг-Оннес.

Сверхпроводящее состояние говорит об исключительных свойствах вещества. Одним из важнейших является способность на протяжении длительного времени поддерживать электрический ток, возбужденный в сверхпроводящей цепи, без затухания.

Классическая электронная теория не может объяснить сверхпроводимость. Это стало возможным спустя 60 лет после его открытия, основываясь на квантово-механических представлениях.

Источник

Электрическое сопротивление металлов. Сверхпроводимость

1. Электрическое сопротивление металлов. Квантовая теория электропроводности металлов сводится к следующему:

а. В идеальной кристаллической решетке электроны проводимости при своем движении не должны испытывать сопротивления. Сопротивление возникает тогда, когда в решетке появляются дефекты структуры, то есть нарушается периодичность решетки.

б. В реальных кристаллах есть два механизма нарушения структуры: примесный и тепловой. Соответственно различают примесное удельное сопротивление r_n и тепловое (колебательное) r_Т. Согласно правилу аддитивности сопротивлений полное сопротивление металла r равно их сумме, r = r_n + r_Т. (13.1)

в. Примесное сопротивление r_n обусловлено наличием инородных атомов в решетке (атомов примеси). Если металл достаточно чистый и концентрация атомов примеси невелика, то примесное сопротивление практически не зависит от температуры и становиться заметным лишь вблизи абсолютного нуля. Благодаря примеси удельное сопротивление металла не должно обращаться в нуль даже при Т = 0 К.

, квантовая теория дает правильный прогноз линейной зависимости r

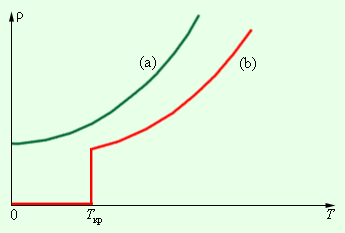
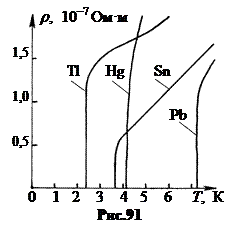
Т. При температурах металла Т ³ 50 К r = r₀aТ, что соответствует эмпирической формуле r = r₀(1 + a t). В квантовой теории получается, что при Т ® 0 полное удельное сопротивление металла r должно стремиться к примесному r_n. На рис.90 показана опытная зависимость удельного сопротивления чистого натрия от температуры.

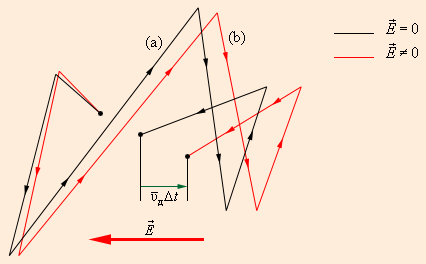
д. Электрический ток толкуется в квантовой теории как дрейф электронов в периодическом поле кристалла. Этот дрейф происходит под действием постоянной электрической силы еЕ, где Е— напряженность электрического поля, создающего ток. Оказалось, что скорость дрейфа электронов зависит от глубины их положения в зоне проводимости. Эта зависимость выражается через эффективную массу m_эф электрона. В отличие от массы покоя m_е свободного электрона эффективная масса электрона в зоне проводимости металла – величина переменная, зависящая от ширины зоны.

Вблизи дна зоны эффективная масса электронов положительна. Направление дрейфа соответствует вектору плотности тока. По мере подъема к верхней границе зоны эффективная масса принимает бесконечно большое значение m_эф = ¥, а затем становится отрицательной. Соответственно и скорость дрейфа электронов, имея “правильное” направление у дна зоны, постепенно проходит через нуль и принимает отрицательные (“неправильные”) значения у верхней границы зоны.

Соотношения, полученные в приближении свободных электронов в теории Друде – Лоренца, оказываются справедливыми для электронов, движущихся в периодическом поле решетки, если в них заменить массу покоя электрона m_е на эффективную m_эф.

2. Сверхпроводимость. В 1911 году Камерлинг – Оннес, измеряя сопротивление ртути в области низких температур, обнаружил, что при Т = 4,2 К сопротивление ртути практически падало до нуля. Это явление стали называть сверхпроводимостью. На рис.91 показаны опытные кривые зависимости удельного сопротивления некоторых чистых металлов от температуры вблизи абсолютного нуля. Очевидно, что явление не сводится к нормальному падению удельного сопротивления бездефектного кристалла, когда r_n = 0, и r_Т . Переход в сверхпроводящее состояние происходит не плавно, а скачкообразно при некоторой температуре Т_кр, которую называют критической температурой перехода. Сейчас известно около 30 сверхпроводящих химических элементов и свыше 500 сверхпроводящих материалов.

3. Эффекты сверхпроводимости.

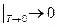
а. Электрический ток, возбужденный в сверхпроводящем кольце, может циркулировать в нем годами.

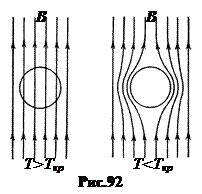
б. ЭффектМейснера. В 1933 году Вальтер Мейсснер и Р. Оксенфельд обнаружили, что вещество, помещенное в магнитное поле (рис.92 слева), при переходе в сверхпроводящее состояние не замораживает находящееся в нем магнитное поле, как это должно было быть при простом переходе вещества в состояние с нулевым сопротивлением, а выталкивает его из своего объема (рис. 92 справа). Это присуще идеальным диамагнетикам с нулевой магнитной проницаемостью m = 0.

Из того, что магнитное поле не проникает в сверхпроводник, следует, что электрический ток может течь лишь по поверхности сверхпроводника. Ведь если бы ток мог протекать в толще сверхпроводника, то вокруг него в толще сверхпроводника было бы магнитное поле. И действительно, опыт показывает, что электрический ток течет в сверхпроводнике в поверхностном слое толщиной l = 10 ¸ 100 нм. На эту глубину в сверхпроводник проникает и магнитное поле, убывая с расстоянием x от поверхности по экспоненциальному закону

Вещество в сверхпроводящем состоянии приобретает два не связанных друг с другом фундаментальных свойства: идеальную проводимость и идеальный диамагнетизм.

Эффект Мейснера позволяет устойчиво подвешивать сверхпроводящие тела в магнитном поле (рис.93). При пререходе шара в сверхпроводящее состояние 1-го рода магнитное поле из него вытесняется. В результате в поверхностном слое шара индуцируется ток такого направления, при котором шар выталкивается из поля.

На рис.94 показана зависимость В_кр от температуры для свинца (верхняя кривая) и для олова (нижняя кривая). При критической температуре Т = Т_кр критическое поле равно нулю, В_кр = 0, а с понижением температуры В_кр увеличивается.

г. Эффект Джозефсона. В 1962 году Брайан Джозефсон теоретически предсказал два эффекта, суть которых в следующем.

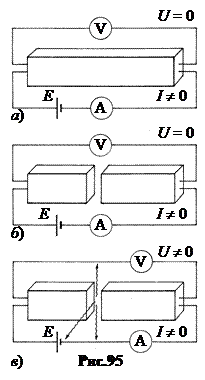
Подсоединим к сверхпроводнику (на рис.95-а он изображен в виде бруска) амперметр А с источником постоянного тока, ЭДС которого E, и вольтметр V. В цепи идёт постоянный ток, регистрируемый амперметром. Так как сопротивление сверхпроводника равно нулю, то вольтметр показывает нуль.

Разрежем сверхпроводник на две части и раздвинем их, чтобы между ними возник зазор толщиной d » 1 нм. Как предсказал Джозефсон, при включении такого сверхпроводника в цепь может наблюдаться один из следующих двух эффектов.

Стационарный эффект Джозефсона. Через сверхпроводник по-прежнему идёт постоянный ток. Оказывается, ток может течь без сопротивления не только через сверхпроводник, но и через щель в нем, если она достаточно узка (рис.95-б).

Нестационарный эффект Джозефсона. На концах сверхпроводника со щелью может возникнуть постоянная разность потенциалов. В этом случае из щели излучается высокочастотная электромагнитная волна (рис.95-в). Через сверхпроводник течет не только постоянный, но и высокочастотный переменный ток.

В настоящее время эффекты Джозефсона не только подтверждены экспериментально, но и используются в микроэлектронике.

4. Теорию сверхпроводимости построили в 1957г Джон Бардин, Леон Купер и Джон Шриффер. По первым буквам их фамилий ее назвали БКШ – теорией. В основе БКШ- теории лежит представление, что между электронами проводимости металла могут действовать силы притяжения, возникающие вследствие поляризации ими кристаллической решетки.

Электрон, движущийся в решетке, притягивает к себе положительно заряженные ионы, несколько сближая их, и тем самым создает вдоль пути своего следования избыточный положительный заряд поляризованной решетки, к которому могут быть притянуты другие электроны. Это эквивалентно возникновению силы притяжения между электронами, только действующей не непосредственно, а через поляризованную решетку.

Убыль кинетической энергии электрона должна быть по крайней мере равной 2D. Так что DЕ_к= 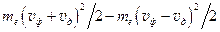= 2m_ev_фv_д = 2D. (13.3)

Отсюда, минимальная скорость дрейфа v_д, необходимая для разрушения куперовской пары, есть v_д = Dçm_ev_ф. (13.4)

Плотность электронного тока проводимости естьj = env_д, (13.5)

где n – концентрация электронов проводимости в металле. Подставив критическую скорость дрейфа из (13.4), получаем критическую плотность тока j_кр.

6. Объяснение БКШ-теорией критического магнитного поля. При помещении сверхпроводника в магнитное поле В в поверхностном слое сверхпроводника наводится незатухающий ток. Этот незатухающий ток имеет такие величину и направление, что его магнитное поле внутри сверхпроводника полностью компенсирует внешнее поле В. При увеличении поля В плотность компенсирующего тока в сверхпроводнике растет. Если внешнее поле В будет настолько большим, что плотность наведенного им индукционного тока достигнет критического значения, сверхпроводимость разрушается.

Все выше сказанное относится к сверхпроводникам 1-го рода, в которых электрический ток существует только в приповерхностном слое. Несколько позже были открыты и изучены сверхпроводники 2-го рода. В них возникающие во внешнем магнитном поле В сверхпроводящие токи текут не только по поверхности, но и проникают в толщу проводника. У сверхпроводников 1-го рода критическое магнитное поле В_кр не превышает 0,1 Тл, а у сверхпроводников 2-го рода достигает величины В_кр» 20 Тл.

При напряжении на щели U = 1 мВ частота n = 485 ГГц, что соответствует длине волны ЭМ излучения l = сçn = 0,6 мм.

8. Реактивное сопротивление сверхпроводника. При любой температуре Т

Источник

Физика. 10 класс

Конспект урока

Урок 32. Электрический ток в металлах

Перечень вопросов, рассматриваемых на уроке:

1) прохождение тока в металлах;

2) зависимость сопротивления металлов от температуры;

3) явление сверхпроводимости.

Свободные электроны – это электроны, не связанные с определенными атомами.

Сверхпроводимость – физическое явление, заключающееся в скачкообразном падении до нуля сопротивления вещества.

Основная и дополнительная литература по теме урока:

Мякишев Г. Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 216-224.

М.М. Балашов О природе М., Просвещение, 1991г.

Е.А. Марон, А.Е. Марон Сборник качественных задач по физике. М., Просвещение, 2006

Я.И. Перельман Занимательная физика. М.: “Наука”, 1991.

Основное содержание урока

Все тела по проводимости электрического тока делятся на проводники, полупроводники и диэлектрики. Для того чтобы электрическую энергию доставить от источника тока потребителю составляют электрические цепи. В большинстве случаев в электрической цепи используются металлические провода. По физической природе зарядов – носителей электрического тока, электропроводность подразделяют на:

Какие заряженные частицы движутся в металлах при наличии тока?

После открытия в 1897 году английским ученым Дж. Дж. Томсоном электрона стали разрабатываться теории, объясняющие электропроводность металлов. Автором первой теории был Пауль Друде – немецкий физик. Эта теория нуждалась в опытном обосновании. В 1901 г. немецкий физик Э. Рикке поставил опыт по исследованию прохождения тока в металлах.

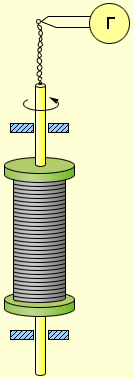
Результаты опыта свидетельствовали о том, что в переносе заряда в металлах ионы не участвуют. Впоследствии вопросом проводимости металлов заинтересовались и другие учёные. В 1913 году российские учёные Л. И. Мандельштам и Н. Д. Папалекси провели опыты по исследованию проводимости металлов. Суть опытов сводилась к тому, что катушка, на которую наматывали металлическую проволоку приводили во вращательное движение и резко тормозили. При торможении электроны продолжали двигаться по инерции и гальванометр, соединенный с катушкой фиксировал появление тока. По направлению отклонения стрелки гальванометра было установлено, что ток создается движением отрицательно заряженных частиц. На основании измерения отношения заряда частиц к их массе выяснилось, что ток создается движением свободных электронов. Аналогичный опыт был поставлен в 1916 году американскими учеными Т. Стюартом и Р. Толменом. Результаты опытов говорили, что ток в металлах создается движением электронов.

После анализа имеющихся данных о прохождении тока в металлах разными учеными была разработана современная классическая теория проводимости тока металлами. Основные положения электронной теории проводимости металлов.

1. Металл можно описать следующей моделью: кристаллическая решетка ионов погружена в идеальный электронный газ, состоящий из свободных электронов. У большинства металлов каждый атом ионизирован, поэтому концентрация свободных электронов приблизительно равна концентрации атомов 1023- 1029м-3 и почти не зависит от температуры.

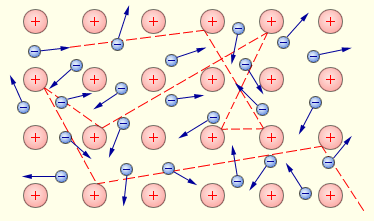
2.Свободные электроны в металлах находятся в непрерывном хаотическом движении.

3. Электрический ток в металле образуется только за счет упорядоченного движения свободных электронов.

Опираясь на данную теорию удалось объяснить основные законы электрического тока в металлах. Исходя из электронной теории можно найти связь между силой тока в металлах и скоростью движения электронов.

Сила тока равна произведению заряда электрона, их концентрации, площади сечения проводника и средней скорости движения электронов:

Отсюда . По этой формуле можно найти среднюю скорость движения электронов.

Если в эту формулу подставлять числовые данные силы тока, концентрации и площади сечения для разных металлов, то мы увидим, что средняя скорость движения электронов составляет всего лишь какие-то доли миллиметра в секунду. Когда говорят о скорости распространения тока имеют в виду скорость распространения электрического поля в проводнике, которое равно скорости света.

На силу тока в проводнике влияет и сопротивление проводника. Опыт показывает, что сопротивление металлов зависит от температуры. Увеличение сопротивления можно объяснить тем, при повышении температуры увеличивается скорость и амплитуда хаотического движения ионов кристаллической решетки металла и свободных электронов. Это приводит к более частым их соударениям, что затрудняет направленное движение электронов, то есть увеличивает электрическое сопротивление.

зависимость сопротивления металлов от температуры выражается формулой:

При нагревании размеры проводника практически не меняются, в основном меняется удельное сопротивление. Учет зависимости сопротивления от температуры используется в термометрах сопротивления.

Формула зависимости удельного сопротивления металлического проводника от температуры имеет вид:

Графиком зависимости ⍴(t) является прямая.

Хотя коэффициент α довольно мал, учет зависимости сопротивления от температуры при расчете нагревательных приборов совершенно необходим.

Вещества, находящиеся в сверхпроводящем состоянии, приобретают новые свойства. Наиболее важным из них является способность длительное время (многие годы) поддерживать без затухания электрический ток в проводниках.

Классическая электронная теория не способна объяснить явление сверхпроводимости. Теоретическое объяснение явления сверхпроводимости на основе квантово-механических представлений было дано учеными Дж. Бардиным, Дж. Шриффером (США) и Н. Н. Боголюбовым (СССР) в 1957 г.

В 1986 году была обнаружена высокотемпературная сверхпроводимость (при 100 К).

В настоящее время ведутся интенсивные работы по поиску новых веществ переходящими в сверхпроводящее состояние при более высокой температуре. Ученые надеются получить вещество в сверхпроводящем состоянии при комнатной температуре. Если удастся создать сверхпроводник при нормальной температуре, то будет решена проблема передачи электроэнергии по проводам без потерь.

Следует отметить, что до настоящего времени механизм высокотемпературной сверхпроводимости керамических материалов до конца не выяснен.

Открытие вещества, переходящего в сверхпроводящее состояние при комнатной температуре, позволило бы упростить решение многих технических вопросов. Во-первых, отсутствие сопротивления означает отсутствие каких-либо потерь на нагревание. Отсутствие нагревания и потерь энергии на него чрезвычайно важно для электродвигателей и электронной вычислительной техники, а также для передачи электроэнергии.

В сверхпроводниках из-за отсутствия сопротивления протекают чрезвычайно высокие токи, создающие сильные магнитные поля, что может применяться при термоядерном синтезе для удержания высокотемпературной плазмы в реакторе.

На сегодняшний момент в некоторых странах существует железнодорожная сеть с поездами на магнитной подушке. После открытия сверхпроводимости Камерлинг-Оннес, пытаясь создать сверхпроводящий электромагнит, обнаружил, что изменение тока, или же магнитные поля, разрушают эффект сверхпроводимости. Только к середине двадцатого века удалось создать сверхпроводящие электромагниты. На данный момент продолжаются исследования по изучению высокотемпературной сверхпроводимости.

Разбор типовых тренировочных заданий

1. Сопротивление железного проводника при 0 0 С и 600 0 С равны соответственно 2 Ом и 10 Ом. Каков температурный коэффициент железа?

Зависимость сопротивления металлов от температуры определяется формулой

Из этой формулы выразим температурный коэффициент железа – α

После подстановки числовых данных получаем

2. Какова скорость дрейфа электронов в медном проводе диаметром 5 мм, по которому к стартеру грузовика подводится ток 100 А. Молярная масса меди

Сила тока в проводнике равна:

Выразим скорость из этой формулы:

Концентрацию электронов найдем по формуле:

Число электронов найдём по формуле:

Площадь сечения равна:

Учитывая всё это запишем конечную формулу для расчёта скорости дрейфа электронов:

Источник