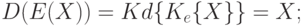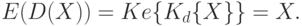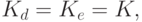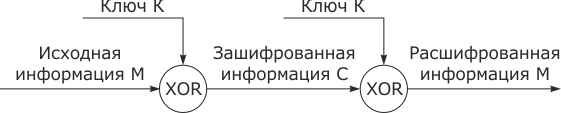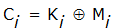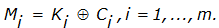чем обеспечивается стойкость системы криптографии
Методы защиты информации в компьютерных системах и сетях
3.4. Криптографические методы защиты
3.4.1. Основные термины и определения
Современная криптография включает в себя следующие основные разделы:
Введем некоторые понятия, необходимые в дальнейшем:
| алфавит | — | конечное множество используемых для шифрования информации знаков; |
| текст | — | упорядоченный набор из элементов алфавита; |
| шифр | — | совокупность обратимых преобразований множества открытых данных на множество зашифрованных данных, заданных алгоритмом криптографического преобразования (криптоалгоритмом); |
| ключ | — | сменный элемент шифра, применяемый для закрытия отдельного сообщения, т.е. конкретное секретное состояние параметров криптоалгоритма, обеспечивающее выбор одного варианта преобразования из совокупности возможных; именно ключом определяется в первую очередь безопасность защищаемой информации и поэтому применяемые в надежных шифрах преобразования в большой степени зависят от ключа; |
| зашифрование | — | преобразование открытых данных в закрытые (зашифрованные) с помощью определенных правил, содержащихся в шифре; |
| расшифрование | — | обратный процесс; |
| шифрование | — | процесс зашифрования или расшифрования; |
| криптосистема | — | состоит из пространства ключей, пространства открытых текстов, пространства шифротекстов и алгоритмов зашифрования и расшифрования; |
| дешифрование | — | процесс преобразования закрытых данных в открытые при неизвестном ключе и (или) неизвестном алгоритме (вскрытие или взлом шифра); |
| синхропосылка | — | исходные параметры криптоалгоритма; |
| раскрытие криптоалгоритма | — | результат работы криптоаналитика, приводящий к возможности эффективного определения любого зашифрованного с помощью данного алгоритма открытого текста; |
| стойкость криптоалгоритма | — | способность шифра противостоять всевозможным попыткам его раскрытия, т.е. атакам на него. |
3.4.2. Оценка надежности криптоалгоритмов
Все современные шифры базируются на принципе Кирхгофа, согласно которому секретность шифра обеспечивается секретностью ключа, а не секретностью алгоритма шифрования. В некоторых ситуациях (например, в военных, разведывательных и дипломатических ведомствах) нет никаких причин делать общедоступным описание сути криптосистемы. Сохраняя такую информацию в тайне, можно дополнительно повысить надежность шифра. Однако полагаться на секретность этой информации не следует, так как рано или поздно она будет скомпрометирована. Поэтому анализ надежности таких систем всегда должен проводиться исходя из того, что противник имеет всю информацию о применяемом криптоалгоритме, ему неизвестен только реально использованный ключ. В связи с вышеизложенным можно сформулировать общее правило: при создании или при анализе стойкости криптосистем не следует недооценивать возможностей противника. Их лучше переоценить, чем недооценить.
Методы оценки качества криптоалгоритмов, используемые на практике:
В первом случае многое зависит от квалификации, опыта, интуиции криптоаналитиков и от правильной оценки возможностей противника. Обычно считается, что противник знает шифр, имеет возможность его изучения, знает некоторые характеристики открытых защищаемых данных, например тематику сообщений, их стиль, стандарты, форматы и т.п.
Во втором случае оценку стойкости шифра заменяют оценкой минимальной сложности алгоритма его вскрытия. Однако получение строгих доказуемых оценок нижней границы сложности алгоритмов рассматриваемого типа проблематично. Иными словами, всегда возможна ситуация, когда алгоритм вскрытия шифра, сложность которого анализируется, оказывается вовсе не самым эффективным.
Сложность вычислительных алгоритмов можно оценивать числом выполняемых элементарных операций, при этом необходимо учитывать их стоимость и затраты на их выполнение. В общем случае это число должно иметь строгую нижнюю оценку и выходить за пределы возможностей современных компьютерных систем. Качественный шифр невозможно раскрыть способом более эффективным, нежели полный перебор по всему ключевому пространству, при этом криптограф должен рассчитывать только на то, что у противника не хватит времени и ресурсов, чтобы это сделать.
В третьем случае можно сформулировать следующие необходимые условия стойкости криптосистемы, проверяемые статистическими методами:
Существует много различных криптоалгоритмов, при этом нет ни одного, подходящего для всех случаев. В каждой конкретной ситуации выбор криптоалгоритма определяется следующими факторами:
3.4.3. Классификация методов шифрования информации
Процедуры зашифрования E (encryption) и расшифрования D (decryption) можно представить в следующем виде:
| где | M (message) и C (ciphertext) | — | открытый и зашифрованный тексты; |
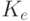 и и 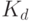 | — | ключи зашифрования и расшифрования. |
Функции за- и расшифрования взаимно обратные, иначе говоря, для любого текста X справедливо:
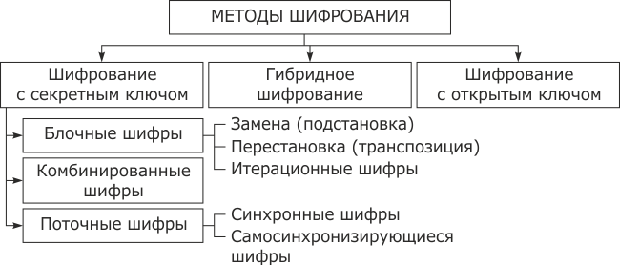
На рис. 3.5 приведена классификация методов шифрования информации. Различают два типа алгоритмов шифрования симметричные (с секретным ключом) и асимметричные (с открытым ключом). В первом случае обычно ключ расшифрования совпадает с ключом зашифрования, т.е.
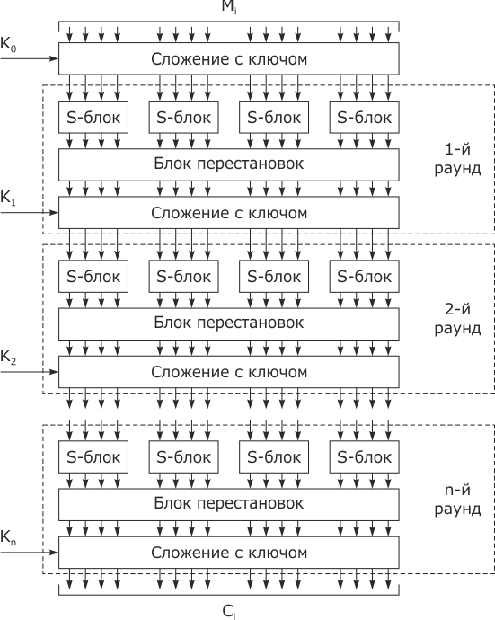
Блочные итерационные шифры. Принцип работы всех современных блочных шифров суть многократное повторение одной и той же раундовой операции. В некоторых случаях раундовые ключи получаются из ключа всей системы с помощью алгоритма выработки раундовых ключей (при этом размер ключа системы существенно меньше суммарного размера всех раундовых ключей).
Идея, лежащая в основе итерационных блочных шифров, состоит в построении криптостойкой системы путем многократного применения относительно простых криптографических преобразований, в качестве которых К. Шеннон предложил использовать преобразования замены (подстановки) (substitution) и перестановки (permutation); схемы, реализующие эти преобразования, называются SP-сетями. Действие таких шифров аналогично «алгоритму», к которому прибегают, когда месят тесто:
Многократное использование этих преобразований, приведенное на рис. 3.6, позволяет обеспечить два свойства, которые должны быть присущи стойким шифрам: рассеивание (diffusion) и перемешивание (confusion) информации.
Рассеивание и перемешивание предполагают:
Наличие у шифра этих свойств:
Интересно отметить, что в первоначальной схеме, предложенной IBM, все шестнадцать 48-разрядных раундовых ключей выбирались независимо, т.е. размер ключа был равен 768 битам. Однако по требованию Агентства национальной безопасности США (АНБ), во-первых, размер ключа был уменьшен до 64 бит, из которых только 56 являются секретными, во-вторых, в алгоритме определены перестановки лишь специального вида, не зависящие от ключа, что наводило критиков этого алгоритма на мысль, будто АНБ могла использовать известные ей слабости алгоритма для его взлома. На протяжении последних десятилетий DES подвергался интенсивному и всестороннему исследованию и по современным понятиям уже не считается надежным, в первую очередь из-за небольшой разрядности ключа.
Существует несколько предложений, направленных на усовершенствование DES. Наиболее известное из них, Triple DES, заключается в трехкратном применении алгоритма.
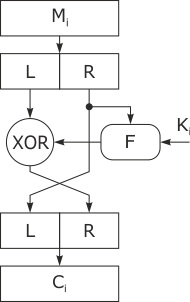
В качестве исходных данных раундовая функция шифрования ГОСТа получает 64-разрядный блок данных D = (L, R) и 32-разрядный раундовый ключ, в качестве которого используется один из элементов ключа Кi. В ходе выполнения преобразования левая L и правая R половины блока данных рассматриваются как отдельные 32-разрядные элементы данных, в качестве которых они подвергаются следующим преобразованиям:
Полученные значения элементов L и R выдаются в качестве результата шага раундового преобразования.
ГОСТ 28147-89 определяет три режима шифрования данных (простая замена, гаммирование и гаммирование с обратной связью) и режим выработки имитоприставки (кода аутентификации сообщений).
3.4.4. Абсолютно стойкий шифр. Гаммирование
Простейшей и в то же время наиболее надежной из всех схем шифрования является так называемая схема однократного использования, приведенная на рис. 3.8, изобретение которой чаще всего связывают с именем Г.С. Вернама.
| где |  , , 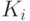 и и 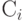 | — | очередной i-й бит соответственно исходного сообщения, ключа и зашифрованного сообщения; |
| m | — | число битов открытого текста. |
Процесс расшифрования сводится к повторной генерации ключевой последовательности и наложения ее на зашифрованные данные. Уравнение расшифрования имеет вид:
К. Шенноном доказано, что, если ключ является фрагментом истинно случайной двоичной последовательностью с равномерным законом распределения, причем его длина равна длине исходного сообщения, и используется этот ключ только один раз, после чего уничтожается, такой шифр является абсолютно стойким, его невозможно раскрыть, даже если криптоаналитик располагает неограниченным запасом времени и неограниченным набором вычислительных ресурсов. Действительно, противнику известно только зашифрованное сообщение С, при этом все различные ключевые последовательности K возможны и равновероятны, а значит, возможны и любые сообщения M, т.е. криптоалгоритм не дает никакой информации об открытом тексте.
Необходимые и достаточные условия абсолютной стойкости шифра:
Таким образом, построить эффективный криптоалгоритм можно, лишь отказавшись от абсолютной стойкости. Возникает задача разработки такого теоретически нестойкого шифра, для вскрытия которого противнику потребовалось бы выполнить такое число операций, которое осуществимо на современных и ожидаемых в ближайшей перспективе вычислительных средствах за разумное время. В первую очередь следует иметь схему, которая использует ключ небольшой разрядности, в дальнейшем выполняющий функцию «зародыша», порождающего значительно более длинную ключевую последовательность.
Данный результат может быть достигнут при использовании гаммирования, схема которого показана на рис. 3.9.
Гаммированием называют процедуру наложения на входную информационную последовательность гаммы шифра, т.е. последовательности с выходов генератора псевдослучайных последовательностей (ПСП) G. Последовательность называется псевдослучайной, если по своим статистическим свойствам она неотличима от истинно случайной последовательности, но в отличие от последней является детерминированной, т.е. знание алгоритма ее формирования дает возможность ее повторения необходимое число раз. Если символы входной информационной последовательности и гаммы представлены в двоичном виде, наложение чаще всего реализуется с помощью операции поразрядного сложения по модулю 2. Надежность шифрования методом гаммирования определяется качеством генератора гаммы.
3.4.5. Генераторы псевдослучайных последовательностей
Качественные ПСП, являясь по своей сути детерминированными, успешно заменяют во многих приложениях (в первую очередь связанных с защитой информации) случайные последовательности, которые чрезвычайно сложно формировать.
Можно выделить следующие задачи, требующие решения при организации защиты информационных систем:
Во всех рассмотренных случаях генераторы ПСП применяются либо непосредственно, либо косвенно, когда на их основе строятся генераторы случайных последовательностей, генераторы контрольных кодов и хеш-генераторы. Во всех случаях требуются последовательности с равномерным законом распределения.
Можно выделить следующие функции генераторов ПСП в системах защиты информации:
Требования к качественному генератору ПСП:
Непредсказуемость. Данное требование означает, что для противника, имеющего возможность анализировать фрагмент ПСП конечной длины, три задачи вычислительно неразрешимы:
Определенные статистические свойства. Это требование означает, что ни один из существующих статистических тестов не в состоянии обнаружить на выходе генератора какие-либо закономерности статистических зависимостей между различными последовательностями, формируемыми при инициализации генератора случайными значениями.
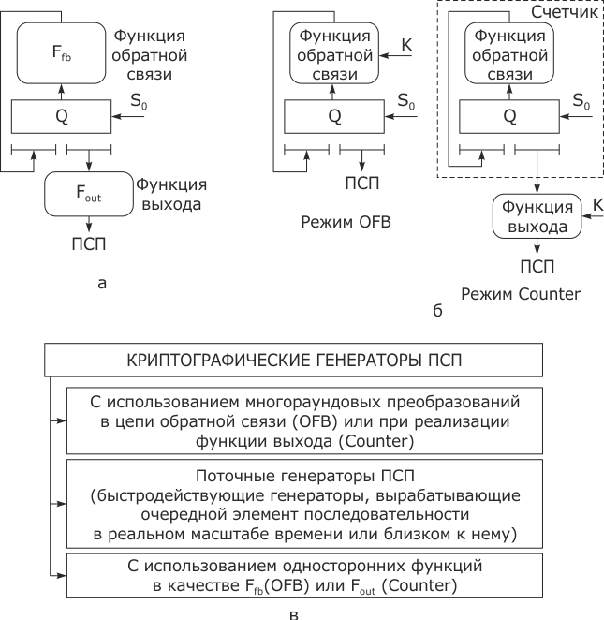
Принципы построения генераторов ПСП. Можно выделить два подхода при использовании в составе генераторов ПСП нелинейных функций: это использование нелинейной функции непосредственно в цепи обратной связи и двухступенчатая схема, в которой задача первой ступени (по сути счетчика) заключается всего лишь в обеспечении максимально большого периода при данном числе N элементов памяти Q. Во втором случае нелинейная функция является функцией выхода 
Вторую схему следует считать более предпочтительной, так как первая имеет следующие недостатки:
На рис. 3.10в показана классификация криптографических генераторов ПСП. Роль нелинейных функций 
Наиболее обоснованными математически следует признать генераторы с использованием односторонних функций. Непредсказуемость данных генераторов основывается на сложности решения ряда математических задач (например, задачи дискретного логарифмирования или задачи разложения больших чисел на простые множители). Существенным недостатком генераторов этого класса является низкая производительность.
3.4.6. Поточные шифры
Шифр Вернама можно считать исторически первым поточным шифром. Так как поточные шифры в отличие от блочных осуществляют поэлементное шифрование потока данных без задержки в криптосистеме, их важнейшим достоинством является высокая скорость преобразования, соизмеримая со скоростью поступления входной информации. Таким образом обеспечивается шифрование практически в реальном масштабе времени вне зависимости от объема и разрядности потока преобразуемых данных.
В синхронных поточных шифрах (см. рис. 3.9) гамма формируется независимо от входной последовательности, каждый элемент (бит, символ, байт и т.п.) которой таким образом шифруется независимо от других элементов. В синхронных поточных шифрах отсутствует эффект размножения ошибок, т.е. число искаженных элементов в расшифрованной последовательности равно числу искаженных элементов зашифрованной последовательности, пришедшей из канала связи. Вставка или выпадение элемента зашифрованной последовательности недопустимы, так как из-за нарушения синхронизации это приведет к неправильному расшифрованию всех последующих элементов.
Криптографическая стойкость
Криптографическая стойкость (или криптостойкость) — способность криптографического алгоритма противостоять возможным атакам на него. Атакующие криптографический алгоритм используют методы криптоанализа. Стойким считается алгоритм, который для успешной атаки требует от противника недостижимых вычислительных ресурсов, недостижимого объёма перехваченных открытых и зашифрованных сообщений или же такого времени раскрытия, что по его истечению защищенная информация будет уже не актуальна, и т. д.
Содержание
Типы криптостойких систем шифрования [ ]
Абсолютно стойкие системы [ ]
Доказательство существования абсолютно стойких алгоритмов шифрования было выполнено К. Шенноном и опубликовано в работе «Теория связи в секретных системах». Там же определены требования к такого рода системам:
Стойкость этих систем не зависит от того, какими вычислительными возможностями обладает криптоаналитик. Практическое применение систем, удовлетворяющих требованиям абсолютной стойкости, ограничено соображениями стоимости и удобства пользования.
Некоторыми аналитиками утверждается, что Шифр Вернама является одновременно абсолютно криптографически стойким и к тому же единственным шифром, который удовлетворяет этому условию.
Достаточно стойкие системы [ ]
В основном применяются практически стойкие или вычислительно стойкие системы. Стойкость этих систем зависит от того, какими вычислительными возможностями обладает криптоаналитик. Практическая стойкость таких систем базируется на теории сложности и оценивается исключительно на какой-то определенный момент времени и последовательно c двух позиций:
В каждом конкретном случае могут существовать дополнительные критерии оценки стойкости.
Оценка криптостойкости систем шифрования [ ]
Начальная оценка [ ]
Текущая оценка [ ]
Дальнейшее исследование алгоритма с целью поиска слабостей (уязвимостей) (криптоанализ) добавляет оценки стойкости по отношению к известным криптографическим атакам (Линейный криптоанализ, дифференциальный криптоанализ и более специфические) и могут понизить известную стойкость.
Важность длительной проверки и открытого обсуждения [ ]
Чем более длительным и экспертным является анализ алгоритма и реализаций, тем более достоверной можно считать его стойкость. В нескольких случаях длительный и внимательный анализ приводил к снижению оценки стойкости ниже приемлемого уровня (например, в черновых версиях FEAL). Недостаточная проверка (по мнению многих криптографов — искусственное ослабление) алгоритма потокового шифрования A5/1 привела к успешной атаке (см…).
Механизмы защиты информации
Криптографические методы защиты информации
Криптография (от древне-греч. κρυπτος – скрытый и γραϕω – пишу) – наука о методах обеспечения конфиденциальности и аутентичности информации.
Криптография представляет собой совокупность методов преобразования данных, направленных на то, чтобы сделать эти данные бесполезными для злоумышленника. Такие преобразования позволяют решить два главных вопроса, касающихся безопасности информации:
Проблемы защиты конфиденциальности и целостности информации тесно связаны между собой, поэтому методы решения одной из них часто применимы для решения другой.
Известны различные подходы к классификации методов криптографического преобразования информации. По виду воздействия на исходную информацию методы криптографического преобразования информации могут быть разделены на четыре группы:
Процесс шифрования заключается в проведении обратимых математических, логических, комбинаторных и других преобразований исходной информации, в результате которых зашифрованная информация представляет собой хаотический набор букв, цифр, других символов и двоичных кодов.
Для шифрования информации используются алгоритм преобразования и ключ. Как правило, алгоритм для определенного метода шифрования является неизменным. Исходными данными для алгоритма шифрования служит информация, подлежащая зашифрованию, и ключ шифрования. Ключ содержит управляющую информацию, которая определяет выбор преобразования на определенных шагах алгоритма и величины операндов, используемых при реализации алгоритма шифрования. Операнд – это константа, переменная, функция, выражение и другой объект языка программирования, над которым производятся операции.
В отличие от других методов криптографического преобразования информации, методы стеганографии позволяют скрыть не только смысл хранящейся или передаваемой информации, но и сам факт хранения или передачи закрытой информации. В основе всех методов стеганографии лежит маскирование закрытой информации среди открытых файлов, т.е. скрываются секретные данные, при этом создаются реалистичные данные, которые невозможно отличить от настоящих. Обработка мультимедийных файлов в информационных системах открыла практически неограниченные возможности перед стеганографией.
Графическая и звуковая информация представляются в числовом виде. Так, в графических объектах наименьший элемент изображения может кодироваться одним байтом. В младшие разряды определенных байтов изображения в соответствии с алгоритмом криптографического преобразования помещаются биты скрытого файла. Если правильно подобрать алгоритм преобразования и изображение, на фоне которого помещается скрытый файл, то человеческому глазу практически невозможно отличить полученное изображение от исходного. С помощью средств стеганографии могут маскироваться текст, изображение, речь, цифровая подпись, зашифрованное сообщение.
Скрытый файл также может быть зашифрован. Если кто-то случайно обнаружит скрытый файл, то зашифрованная информация будет воспринята как сбой в работе системы. Комплексное использование стеганографии и шифрования многократно повышает сложность решения задачи обнаружения и раскрытия конфиденциальной информации.
Содержанием процесса кодирование информации является замена исходного смысла сообщения (слов, предложений) кодами. В качестве кодов могут использоваться сочетания букв, цифр, знаков. При кодировании и обратном преобразовании используются специальные таблицы или словари. В информационных сетях кодирование исходного сообщения (или сигнала) программно-аппаратными средствами применяется для повышения достоверности передаваемой информации.
Часто кодирование и шифрование ошибочно принимают за одно и тоже, забыв о том, что для восстановления закодированного сообщения, достаточно знать правило замены, в то время как для расшифровки сообщения помимо знания правил шифрования, требуется ключ к шифру.
Сжатие информации может быть отнесено к методам криптографического преобразования информации с определенными оговорками. Целью сжатия является сокращение объема информации. В то же время сжатая информация не может быть прочитана или использована без обратного преобразования. Учитывая доступность средств сжатия и обратного преобразования, эти методы нельзя рассматривать как надежные средства криптографического преобразования информации. Даже если держать в секрете алгоритмы, то они могут быть сравнительно легко раскрыты статистическими методами обработки. Поэтому сжатые файлы конфиденциальной информации подвергаются последующему шифрованию. Для сокращения времени передачи данных целесообразно совмещать процесс сжатия и шифрования информации.
За многовековую историю использования шифрования информации человечеством изобретено множество методов шифрования или шифров. Методом шифрования (шифром) называется совокупность обратимых преобразований открытой информации в закрытую информацию в соответствии с алгоритмом шифрования. Большинство методов шифрования не выдержали проверку временем, а некоторые используются и до сих пор. Появление компьютеров и компьютерных сетей инициировало процесс разработки новых шифров, учитывающих возможности использования компьютерной техники как для зашифрования/расшифрования информации, так и для атак на шифр. Атака на шифр (криптоанализ, криптоатака) – это процесс расшифрования закрытой информации без знания ключа и, возможно, при отсутствии сведений об алгоритме шифрования.
Современные методы шифрования должны отвечать следующим требованиям:
Криптостойкость шифра является его основным показателем эффективности. Она измеряется временем или стоимостью средств, необходимых криптоаналитику для получения исходной информации по шифртексту, при условии, что ему неизвестен ключ.
Сохранить в секрете широко используемый алгоритм шифрования практически невозможно. Поэтому алгоритм не должен иметь скрытых слабых мест, которыми могли бы воспользоваться криптоаналитики. Если это условие выполняется, то криптостойкость шифра определяется длиной ключа, так как единственный путь вскрытия зашифрованной информации – перебор комбинаций ключа и выполнение алгоритма расшифрования. Таким образом, время и средства, затрачиваемые на криптоанализ, зависят от длины ключа и сложности алгоритма шифрования.
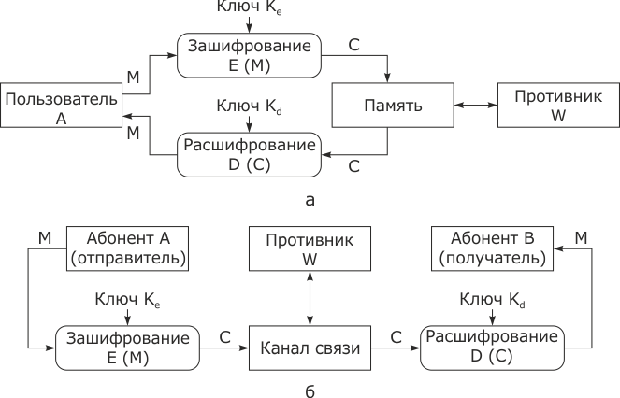
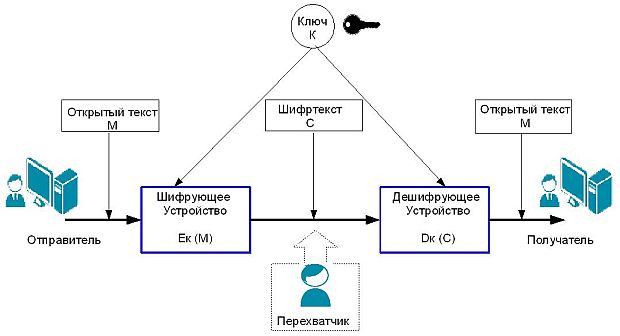
Работа простой криптосистемы проиллюстрирована на рис. 2.2.
Законный получатель, приняв шифртекст С, расшифровывает его с помощью обратного преобразования Dк(С) и получает исходное сообщение в виде открытого текста М.
Преобразование Ек выбирается из семейства криптографических преобразований, называемых криптоалгоритмами. Параметр, с помощью которого выбирается отдельное преобразование, называется криптографическим ключом К.
Криптосистема имеет разные варианты реализации: набор инструкций, аппаратные средства, комплекс программ, которые позволяют зашифровать открытый текст и расшифровать шифртекст различными способами, один из которых выбирается с помощью конкретного ключа К.
Преобразование шифрования может быть симметричным и асимметричным относительно преобразования расшифрования. Это важное свойство определяет два класса криптосистем:
Симметричное шифрование, которое часто называют шифрованием с помощью секретных ключей, в основном используется для обеспечения конфиденциальности данных. Для того чтобы обеспечить конфиденциальность данных, пользователи должны совместно выбрать единый математический алгоритм, который будет использоваться для шифрования и расшифровки данных. Кроме того, им нужно выбрать общий (секретный) ключ, который будет использоваться с принятым ими алгоритмом шифрования/дешифрования, т.е. один и тот же ключ используется и для зашифрования, и для расшифрования (слово «симметричный» означает одинаковый для обеих сторон).
Пример симметричного шифрования показан на рис. 2.2.
Сегодня широко используются такие алгоритмы шифрования, как Data Encryption Standard (DES), 3DES (или «тройной DES») и International Data Encryption Algorithm (IDEA). Эти алгоритмы шифруют сообщения блоками по 64 бита. Если объем сообщения превышает 64 бита (как это обычно и бывает), необходимо разбить его на блоки по 64 бита в каждом, а затем каким-то образом свести их воедино. Такое объединение, как правило, происходит одним из следующих четырех методов:
Triple DES (3DES) – симметричный блочный шифр, созданный на основе алгоритма DES, с целью устранения главного недостатка последнего – малой длины ключа (56 бит), который может быть взломан методом полного перебора ключа. Скорость работы 3DES в 3 раза ниже, чем у DES, но криптостойкость намного выше. Время, требуемое для криптоанализа 3DES, может быть намного больше, чем время, нужное для вскрытия DES.
Алгоритм AES (Advanced Encryption Standard), также известный как Rijndael – симметричный алгоритм блочного шифрования – шифрует сообщения блоками по 128 бит, использует ключ 128/192/256 бит.
Шифрование с помощью секретного ключа часто используется для поддержки конфиденциальности данных и очень эффективно реализуется с помощью неизменяемых «вшитых» программ (firmware). Этот метод можно использовать для аутентификации и поддержания целостности данных.
С методом симметричного шифрования связаны следующие проблемы: