чем можно описать простую трехмерную систему погоды
Теория хаоса
Что такое «странные аттракторы» и как они помогают синоптикам
Можно ли прогнозировать хаотическое движение элементов какой-либо системы? От чего зависит хаотическая динамика? Может ли, наконец, взмах крыла бабочки вызвать торнадо? Некоторые важные ответы на эти и другие вопросы нашел американский метеоролог Эдвард Лоренц, (невольный) автор термина «эффект бабочки» и создатель «странного аттрактора». Рассказываем об этом в первом материале, посвященном самым интересным дифференциальным уравнениям.
В 1972 году профессор метеорологии из Массачусетского технологического института Эдвард Лоренц собирался выступить на конференции, но в пылу работы не успел отправить тему своей лекции. Организатор, спешивший разослать приглашения, выбрал заголовок за него: «Предсказуемость: может ли взмах крыла бабочки в Бразилии вызвать торнадо в Техасе?» Так и появился термин «эффект бабочки», известный сегодня всему миру.
Эдвард Лоренц родился в 1917 году в небольшом городке в штате Коннектикут. Изучать атмосферные явления он решил еще в детстве, испытав потрясение от того, с какой легкостью солнечная погода может смениться бурей с громом и молниями.
Путь к исполнению мечты вышел долгим: магистратура в Гарварде, работа метеорологом в авиационном подразделении Армии США, защита диссертации в послевоенный период, наконец, должность научного сотрудника и, позже, профессора в MIT.
В своем выступлении Лоренц выделил несколько ключевых идей:
⦁ Если взмах крыла бабочки может вызвать торнадо, то точно так же на это способны все предыдущие и будущие взмахи, равно как и взмахи остальных миллионов бабочек, не говоря уже об активности бесчисленного населения нашей планеты.
⦁ Если взмах крыла бабочки способен вызывать торнадо, то в равной степени этот же взмах может его предотвратить.
Взмах крыла бабочки в данном контексте должен восприниматься как маленькое изменение начальных условий исследуемой системы, способное как вызвать торнадо, так и изменить его траекторию или вообще стать причиной его затухания.
В отличие от эффекта домино, где конкретное (обычно незначительное) действие приводит к конкретному (обычно значительному) результату, причем происходит это однозначно, взмах бабочки может не иметь никакого влияния на поведение торнадо.
Система Лоренца
Лоренц изучал конвекцию (теплообмен, возникающий за счет движения молекул жидкости или газа) в атмосфере Земли. Для описания подобных физических процессов часто пользуются моделью, которая включает в себя уравнения Навье-Стокса, описывающие движение вязкой ньютоновской жидкости (за исключением некоторых частных случаев, их решения в общем виде на данный момент неизвестны):
⦁ Уравнение движения в векторном виде:
⦁ Уравнение теплопроводности, описывающее распределение температуры в пространстве с течением времени:
⦁ Уравнение непрерывности, которое, по своей сути, описывает принцип сохранения массы чего-либо:
В оригинале эти три составляющие дают следующую систему:
Мы не будем углубляться в детальное объяснение всего вышеизложенного. Достаточно лишь понимать, что это довольно сложная модель, и Лоренцу в результате многостраничных выкладок удалось построить ее упрощение:
Здесь переменная с точкой сверху означает ее производную по времени. Более подробно:
С помощью этой системы уравнений можно рассчитать, как будет вести себя текучая среда, которую равномерно разогревают снизу и охлаждают сверху. Так, как это происходит с воздушными потоками в атмосфере. В частности, она позволяет понять, к какому результату приведет даже небольшое изменение исходных параметров.
Хаотическое движение
Перед тем как приступить к непосредственному анализу полученной системы, рассмотрим некоторые комбинации траекторий. Для наглядности, воспользуемся теми же значениями параметров, что и сам Лоренц: σ = 10, ρ = 28, β = 8/3.
Изобразим движение двух точек, расстояние между которыми изначально невелико:
Довольно интересный результат! Поначалу траектории почти неразличимы, потом они отклоняются совсем ненамного, после чего разница становится уже значительной.
Попробуем еще раз, однако теперь возьмем точки на значительном отдалении друг от друга:
Даже несмотря на подобную разницу начальных условий, траектории попадают на фигуру, которую впоследствии не покидают. Очень странно, их будто что-то притягивает…
Странный аттрактор Лоренца
Действительно, эта фигура так и называется — странный аттрактор Лоренца (от английского attract — «притягивать»).
Формальное математическое определение звучит так: аттрактор — такое подмножество фазового пространства, что все траектории, стартующие не слишком далеко от него, стремятся к нему с течением времени. (Это одно из возможных определений понятия аттрактора, существуют и другие, не эквивалентные данному.)
Слово же «странный» здесь выступает в таком ключе: аттрактор как множество не представим в виде кривой или поверхности, он имеет более сложную, фрактальную структуру. Траектории аттрактора не замыкаются, а малые отклонения постоянно накапливаются, причем экспоненциально.
Сказанное выше можно проиллюстрировать так: две траектории, выпущенные из близких точек, со временем разбегаются достаточно далеко. Причем, чтобы отдалить момент разбегания, например, на одну секунду, нужно уменьшить расстояние между начальными точками, скажем, вдвое. А чтобы на две секунды — вчетверо. А на три — в восемь раз, и так далее.
Это означает, что, даже используя мощный компьютер, мы не можем просчитать траекторию, проходящую вблизи аттрактора, с разумной точностью на протяжении длительного промежутка времени. На каждом шаге вычислений неизбежно вносятся ошибки (из-за округления чисел и погрешностей численных методов), которые быстро накапливаются и приводят к тому, что найденная траектория сильно отличается от настоящей.
Такое искажение невозможно исправить, просто увеличивая мощность компьютера. Подобное явление называется «динамическим хаосом».
Ниже представлена модель странного аттрактора, с которой можно поэкспериментировать, меняя входящие значения. Для желающих более подробно изучить математическую сторону припасен еще один раздел сразу после модели.
Вы можете покрутить модель или увеличить/уменьшить ее масштаб (с помощью кнопок мыши на десктопе или пальцами на экране смартфона). Значение бегунков сверху вниз:
Немного математики
Система Лоренца обладает несколькими замечательными свойствами:
⦁ Правая часть системы не имеет свободных членов, то есть она однородна.
Краткое введение в Теорию Хаоса
Все в мире целиком и полностью имеет свои причины и последствия. Возможно, эта мысль навела меня на осознание того, что все в мире взаимосвязано. Всему есть свои причины. Даже в случайности заложено движение к какой-то цели.
События, кажущиеся случайными, происходят в определенной последовательности.
Что в точности есть хаос? Название «Теория Хаоса» произошло благодаря тому факту, что системы, описываемые теорией, взятые по кусочкам- неупорядочены, но Теория Хаоса на самом деле заключается в том, чтобы найти скрытый порядок в кажущихся случайными данных.
Когда был открыт Хаос? Первый истинный экспериментатор в области Хаоса был метеоролог Эдвард Лоренс. В 1960 году он работал над проблемой предсказания погоды. У него была компьютерная установка с набором из 12 уравнений, моделирующих погоду (имеются ввиду воздушные потоки в атмосфере)[уточнение тут]. Они сами по себе не предсказывали погоду. Но как бы то ни было, компьютерная программа теоретически предсказывала, какой могла быть погода.
Однажды в 1961 году он [Эдвард Лоренс] снова захотел посмотреть особенную последовательность. Чтобы сэкономить время, он начал с середины последовательности, вместо того, чтобы сделать это сначала. Он ввел числа из распечатки и запустил программу…
Когда он вернулся часом позже, закономерность была решена по-другому. Вместо той же модели, что была прежде, была модель, отклоняющаяся в конце очень сильно, отличаясь от оригинальной (см. Рисунок 1). В конце –концов он выяснил, что произошло. Компьютер поместил в память 6 чисел после запятой. Чтобы сэкономить бумагу, он вводил только 3 числа после запятой. В оригинальном порядке было число 0.0506127, а он напечатал только 0.506.
Рисунок 1 – Эксперимент Лоренса: разница в начале между этими кривыми всего лишь 0.000127(Ян Стюарт, «Does God Play Dice?», Математика Хаоса, стр.141)
По общепринятому мнению того времени это должно было сработать. Он должен был получить порядок очень близкий к оригинальному. Ученый мог посчитать себя счастливцем, получив измерения с точностью до 3 чисел после запятой. Конечно, измерить 4-ю и 5-ю цифру, используя рациональные методы, было невозможно, и это не могло повлиять на результат эксперимента. Лоренс посчитал идею неверной. Этот эффект известен как Эффект Бабочки. Разница в начальных точках двух кривых настолько мала, что сравнима с порханием крыльев бабочки [в реальной жизни].
Движение крыльев одной бабочки сегодня создает малейшие изменения состояния атмосферы. По прошествии времени атмосфера отличается от той, какой она могла бы быть. Таким образом, через месяц Торнадо, который мог обрушиться на Индонезию, не появляется. Или, если он не должен был появиться, он появляется.(Ян Стюарт, «Does God Play Dice?», Математика Хаоса, стр.141).
Этот феномен, в общем называемый Теорией Хаоса, также известен как чувствительная зависимость от начальных условий. Всего лишь маленькое изменение в начальных условиях может кардинально изменить поведение системы, рассматриваемой длительный период времени. Такая маленькая разница в измерениях может быть вызвана в эксперименте шумом, фоновым шумом или неисправностью оборудования. Этих вещей невозможно избежать даже в самой изолированной лаборатории.
Начиная с числа 2, в итоге может получиться результат, всецело отличающийся от результатов такой же системы с начальной цифрой 2.000001. Это просто невозможно- достигнуть такого уровня точности- просто попытайтесь измерить что-нибудь с точностью до миллионной доли дюйма!Исходя из этой идеи, Лоренс установил невозможность точного предсказания погоды. Как бы то ни было, это открытие привело Лоренса к другим аспектам того, что впоследствии стало известным как Теория Хаоса.
Лоренс начал наблюдать за простейшими системами, которые чувствительны к разнице в начальных условиях. Его первое открытие имело 12 уравнений, и он хотел его очень упростить, но чтобы оно все же имело этот атрибут[чувствительность к разнице в начальных условиях]. Он взял уравнения конвекции и сделал их неимоверно простыми. Эта система больше не имела отношения к конвекции, но имела чувствительность к разнице в начальных условиях, и на этот раз осталось всего лишь 3 уравнения. Позже было установлено, что эти уравнения описывают водоворот.
На поверхности вода неуклонно образует как бы обод колеса. Каждый «обод» расходится от маленького отверстия Если поток воды имеет маленькую скорость, «ободки» никогда не станут достаточно быстрыми, чтобы образовался водоворот. Вращение может продолжаться. Или, если поток настолько быстрый, что тяжелые «ободы» все время вращаются вокруг дна и поверхности, водоворот может замедлиться, остановиться и поменять направление вращения, вращаясь сначала в одну сторону, а затем в другую. (James Gleick, Теория Хаоса, стр. 29)
Уравнения для этой системы также казалось, показывали общую случайность поведения.Как бы то ни было, когда был построен график, он был удивлен [Лоренс]. Выходные параметры всегда оставались на кривой, образуя двойную спираль. До этого было известно только два типа порядка: постоянное состояние, в котором переменные никогда не меняются, и периодичное состояние, в котором система циклична, и неопределенно повторяется. Уравнения Лоренса были определенно упорядочены- они всегда следовали по спирали. Они никогда не останавливались на одной точке, но никогда не повторяли то же состояние, то есть не были периодичными. Он назвал полученные уравнеия аттрактором Лоренса(см. Рисунок 2).
Рисунок 2 – Аттрактор Лоренса
В 1963 Лоренс опубликовал статью, описывающую его открытие. Он включил туда статью о непредсказуемости погоды и обсудил все типы уравнений, вызвавших этот тип поведения. К несчастью, единственным журналом, в котором он мог опубликовать свою статью, был метеорологический журнал, так как он был не физиком или математиком, a метеорологом. В результате открытия Лоренса не были известны до тех пор, пока не были открыты снова другими людьми. Лоренс открыл нечто революционное, и ждал, пока кто-то откроет его.
Другая система, в которой есть чувствительность к разнице в начальных условиях- бросание монетки. Есть две переменные в бросании монетки: как скоро она упадет и как быстро она вращается. Теоретически, возможно контролировать эти две переменные полностью, и контролировать- как монетка упадет. На практике невозможно контролировать абсолютно точно скорость вращения монеты и то, насколько она подлетит. Возможно только поместить эти переменные в определенном диапазоне, но невозможно контролировать их настолько, чтобы знать результат.
Схожая проблема имеет место в экологии и предсказании биологических популяций. Уравнение простое, если популяция растет определенно, но хищники и ограниченность в пище делают это уравнение неверным. Самое простое уравнение имеет вид:
next year’s population = r * this year’s population * (1 — this year’s population) [где next year’s population-популяция в следующем году, this year’s population- популяция в этом году]
В этом уравнении популяция описывается числом между 1 и 0, где 1 представляет собой максимально возможную популяцию, а 0- вымирание. R- показатель роста. Вопрос состоял в том, как этот параметр влияет на популяцию? Очевидный ответ- высокий показатель роста популяции значит установление высокого уровня, в то время как низкий означает, что популяция упадет. Это условие истинно для некоторых показателей роста, но не для всех.
Биолог Роберт Мэй, решил выяснить, что случится с уравнением, если повышать показатель роста. При низких значениях популяция устанавливалась на каком-либо определенном значении. Для показателя равного 2.7 она устанавливалась на уровне 0.6292. Далее при увеличении показателя роста популяции«R», итоговая популяция также росла. Но затем случалось нечто странное.
Как только показатель превышал 3, линия разделялась надвое. Вместо устанавливания в каком-то определенном положении, она «прыгала» между двумя различными значениями. Она имела одно значение в одном году, и совершенно иное- в следующем. И так этот цикл повторялся постоянно. Повышение показателя роста вызывало скачки между двумя разными значениями.
Как только параметр повышался далее, линия бифурцировала(раздваивалась) снова. Бифуркации происходили быстрее и быстрее, до тех пор, пока неожиданно не становились хаотичными. Устанавливая точный показатель роста невозможно предсказать поведение уравнения. Как бы то ни было, при ближайшем исследовании можно увидеть белые полоски. Посмотрев на эти полоски ближе обнаруживаем ряд маленьких окон, где через бифуркации проходит линия, перед тем, как вновь вернуться к состоянию хаоса. Эта похожесть на саму себя,- факт того, что график- точная копия его самого, спрятанного глубоко внутри.Это стало очень важным аспектом хаоса.(рисунок 3)
Рисунок 3- Бифуркация
Служащий IBM Бенуа Мандельброт был математиком, изучавшим эту самопохожесть. Одной из областей, которые он изучал, было колебание цен на хлопок. Неважно, как были проанализированы данные о ценах на хлопок, результаты не были распределенными нормально. Мандельброт в конечном счете получил все доступные данные о ценах на хлопок, вплоть до 1900 года. Когда он проанализировал данные с помощью ЭВМ, он заметил поразительный факт:число с точки зрения нормальных продаж было симметрично относительно точки зрения в масштабе. Каждая отдельная цена менялась случайно и непредсказуемо. Но расчет изменений был независим от масштабов: кривые дневных и месячных колебаний цен абсолютно совпадали. Поразительно, но проанализированные Мандельбротом изменения цен оставались постоянными на протяжении всего шумного периода 60-х, Второй Мировой и депрессии.( James Gleick, Chaos — Making a New Science, стр. 86)
Мандельброт проанализировал не только цены на хлопок, но и другие явления. Одним из них была протяженность береговой линии. Карта побережья показывает множество заливов. Но как бы то ни было, при подсчете длины береговой линии будут упущены мелкие заливы, которые слишком малы, чтобы быть показанными на карте. Это подобно тому, как при прогулке по берегу мы пропускаем микроскопические промежутки между песчинками. Неважно, насколько увеличить линию побережья, будет больше видимых промежутков при приближении.
Один математик, Хельге вон Кох взл эту идею для математического конструирования, названного кривой Коха. Чтобы создать кривую Коха, представьте равносторонний треугольник. К середине каждой стороны дорисуйте еще по равностороннему треугольнику.Продолжайте добавлять новые треугольники к серединам каждой из сторон, и в результате получите кривую Коха.(см. Рисунок 4).
Приближенная кривая Коха выглядит точно так же, как и оригинал. Это другой пример самопохожести.
Кривые Коха заключают в себе интересный парадокс. Каждый раз, когда добавляется очередной треугольник, длина линии становится больше. Но как бы то ни было, внутренняя площадь[ограниченная] кривой Коха всегда остается меньше площади описанной окружности вокруг первого треугольника. То есть это линия неограниченной длины, заключенная в ограниченной области.
Чтобы разобраться в этом, математики использовали понятие фрактала. Фрактал происходит от слова дробный. Фрактальное дробление кривой Коха составляет примерно 1.26. Фрактальное дробление невозможно придумать, но оно имеет смысл. Кривая Коха более грубая, чем гладкая кривая линия, у которой единичное дробление. Так как она грубее и более «морщинистая», она лучше занимает пространство. Как бы то ни было, она не так хороша в заполнении пространства как квадрат с двумя дроблениями, поскольку не имеет площади. Это означает, что дробление кривой Коха меньше 2.
Под фракталом имеется ввиду любое изображение, имеющее в себе самопохожесть. Бифуркационная диаграмма уравнения популяции- фрактал. Аттрактор Лоренса- фрактал.Кривая Коха- тоже фрактал.
В это время ученые нашли трудным публиковать работы о Хаосе. С тех пор как они еще не показали его отношение к реальному миру. Большинство ученых не думали, что результаты экспериментов относительно Хаоса важны. Как результат, даже несмотря на то, что Хаос- математический феномен, большинство исследований в области Хаоса были сделаны людьми, являющимися специалистами в других областях, таких как метеорология и экология. Изучение области распространения Хаоса – было хобби для ученых, работающих над проблемой, что же с этим делать.
Позже, ученый по фамилии Фигенбаум снова исследовал диаграмму бифуркации.Он исследовал скорость наступления бифуркации. Он открыл, что она наступает при постоянном показателе. Он вычислил, что это число 4.669. другими словами, он определил точный масштаб при котором кривая бифуркации приобретает свойство самопохожести.
Уменьшенная в 4.669 раз, диаграмма выглядит как последующий регион бифуркации. Он решил посмотреть на другие уравнения чтобы увидеть, возможно ли применить фактор масштаба и к ним. К большому удивлению, фактор масштаба оказался таким же. Не только для сложных уравнений, описывающих закономерность.Закономерность была точно такой же как и у простых уравнений.Он опробовал множество функций, и они давали фактор масштабирования 4.669.
Это было революционным открытием. Он обнаружил целый класс математических функций, ведущих себя одинаково, предсказуемо. Универсальность помогла многим ученым легко анализировать уравнения хаоса. Она дала ученым первые инструменты для анализа хаотических систем. Теперь они могли использовать простые уравнения для получения результата более сложных.
Многие ученые открыли уравнения, создающие фрактальные уравнения. Самое известное изображение фрактала- является и самым простым. Оно известно как уравнение Мандельброта. Уравнение простое: z=z 2 +c. Чтобы выяснить, является ли ваше уравнение таковым, возьмите комплексное число z. Получите его квадрат и затем добавьте число. Введите в квадрат полученный результат и добавьте число. Повторяйте далее, и если число стремится к бесконечности, это не уравнение Мандельброта.
Фрактальные структуры были замечены во многих областях реального мира. Кровь разносится по кровеносным сосудам, ветвящимся дальше и дальше, ветви дерева, структура легких, графики данных о продаже акций, и другие системы раельного мира имеют нечто общее: они все обладают самопохожестью(самоповторением).
Ученые в Университете Санта Круз нашли проявления Хаоса в водопроводном кране[то, как он капает]. Записывая падение капель из крана и периоды времени, они открыли точную скорость потока, капли не падали в то же самое время. Когда они построили графики данных, они нашли, что на самом деле капли падают с определенной закономерностью.
Человеческое сердце тоже бьется с хаотической закономерностью. Время между ударами непостоянно, оно зависит от того, насколько активен человек в данный момент, и от многих других вещей. При постоянных условиях сердцебиение все равно может ускориться. При различных условиях сердце бьется неуправляемо. Это можно назвать хаотичным сердцебиением. Анализы сердцебиения могут помочь в медицинских исследованиях найти способ установить сердцебиение в определенных рамках, вместо неконтролируемой хаотичности.
Хаос имеет применение даже в науке. Компьютерные изображения становятся более реалистичными при применении Хаоса и фракталов. Сейчас с помощью простой формулы можно создать на компьютере красивое реалистично выглядещее дерево. Вместо того, чтобы следовать нормальной закономерности, ветки деревьев могут быть созданы по формуле, которая почти, но не точно повторяет себя.
Также с помощью фракталов может быть создана музыка. Используя аттрактор Лоренса, Диана С. Дэбби, выпускница по специальности электронной инженерии Массачусетского Института Технологий, создала музыкальные темы. («Bach to Chaos: Chaotic Variations on a Classical Theme», Science News, Dec. 24, 1994). Путем ассоциирования музыкальных нот фрагмента музыки из Прелюдии Баха в С с координатами х аттрактора Лоренса, запустив программу на компьютере, она создала вариации на тему данного произведения. Большинство музыкантов, слышавших эти новые звуки, говорили, что вариации очень музыкальны и креативны.
UPD: Благодарю ixside. «Chaotic Variations on a Classical Theme» доступны тут.Правка: перенесено в Научно-популярное.
Аттрактор и бабочка Памяти Эдварда Нортона Лоренца
В 1961 году метеоролог и математик Эдвард Лоренц, скончавшийся 16 апреля 2008 года, ввел в созданную им компьютерную модель погоды данные, округлив их не до шестого, а до третьего знака после запятой. В результате был сформулирован эффект бабочки, открыт один из странных аттракторов, обнаружена непредсказуемость поведения многих детерминированных систем и, в конечном итоге, создана теория хаоса.
Предыстория: демон Лапласа
Вопрос: мыслим ли такой демон хотя бы теоретически? Успехи науки Нового времени наводили на мысль, что да: орбиты планет были рассчитаны, появления комет – предсказаны, случайные события – описаны теорией вероятности.
В дальнейшем, однако, демон Лапласа подвергся жесткой критике. После развития квантовой механики и открытия принципа неопределенности Гейзенберга (нельзя точно измерить одновременно скорость и координаты частицы) стало понятно, что квантовые системы демону неподвластны: в них есть принципиальная непредсказуемость.
Впоследствии также отмечалось, что существование демона противоречило бы законам термодинамики, что ему в принципе не хватило бы для знаний и вычислений информационных мощностей, даже используй он все ресурсы Вселенной.
Однако демон не сдал позиции полностью. В самом деле, представим себе полностью детерминированную (предопределенную, лишенную случайности) систему (классическую, без квантовых эффектов). Если мы знаем все законы, управляющие ее поведением (будь они сколь угодно сложны), знаем все необходимые параметры и обладаем необходимыми вычислительными мощностями (то есть под рукой есть демон Лапласа – читай: суперкомпьютер), то уж для такой-то системы мы сможем полностью предсказать поведение?
Есть одна оговорка. Все наши измерения будут содержать какую-нибудь ошибку. Переменные, хранящиеся в памяти компьютера, будут иметь ограниченную точность. То есть придется пользоваться приблизительными данными. Ну и ладно: нам не нужна бесконечная точность, вполне достаточно приблизительных предсказаний. Исходные данные содержат ошибку в пятом знаке? Ошибка предсказания в пятом знаке нас вполне устроит.
Итак, можно ли, например, предсказывать погоду? Хотя бы примерно? Хотя бы на каком-то ограниченном участке, но на более-менее приличный срок?
Три знака после запятой
Эдвард Лоренц. Фото с сайта Американского физического института.
В его распоряжении находилась вычислительная машина Royal McBee. В 1960 году Лоренц создал упрощенную модель погоды. Модель представляла собой набор чисел, описывавший значение нескольких переменных (температуры, атмосферного давления, скорости ветра) в данный момент времени. Лоренц выбрал двенадцать уравнений, описывавших связь между этими переменными. Значение переменных в следующий момент времени зависело от их значения в предыдущий момент и рассчитывалось по этим уравнениям. Таким образом, модель была полностью детерминирована.
Коллеги Лоренца от модели пришли в восторг. Машине скармливались несколько чисел, она начинала выдавать ряды чисел (впоследствии Лоренц научил ее рисовать несложные графики), описывающие погоду в некотором воображаемом мире. Числа не повторялись – они порой почти повторялись, система как будто воспроизводила старое свое состояние, но не полностью, циклов не возникало. Словом, искусственная погода была плохо предсказуема, причем характер этой непредсказуемости (апериодичность) был примерно такой же, какой и у погоды за окном. Студенты и преподаватели заключали пари, пытаясь угадать, каким будет состояние модели в следующий момент.
Зимой 1961 года Лоренц решил подробнее изучить уже построенный машиной график изменения одной из переменных. В качестве начальных данных он ввел значения переменных из середины графика и вышел отдохнуть. Машина должна была бы точно воспроизвести вторую половину графика и продолжить строить его дальше. Однако вернувшись, Лоренц обнаружил совершенно другой график. Если в начале он еще более-менее повторял первый, то к концу не имел с ним ничего общего.
Расхождение двух графиков погоды, берущих начало из одной точки. Распечатка Лоренца 1961 года, воспроизведенная в книге Джеймса Глейка «Хаос: Создание новой науки» (СПб., «Амфора», 2001).
Получалось, что модель, из которой полностью устранена случайность, при одних и тех же начальных значениях выдает совершенно разные результаты. Машина не сломалась и считала все правильно, Лоренц не опечатался при вводе данных.
Разгадка нашлась довольно быстро: в памяти машины значения переменных хранились с точностью до шести знаков после запятой (. 506217), а на распечатку выдавалось только три (. 506). Лоренц, разумеется, ввел округленные значения, резонно предположив, что такой точности вполне достаточно.
Оказалось, что нет. «. овалились маленькие костяшки домино. большие костяшки. огромные костяшки, соединенные цепью неисчислимых лет, составляющих Время», – написал в 1952 году в знаменитом рассказе «И грянул гром» Рэй Брэдбери. Примерно это же произошло в модели Лоренца. Система оказалась исключительно чувствительной к малейшим воздействиям на нее.
Эффект бабочки
Откуда в детерминированной системе хаос и непредсказуемость? От сильной чувствительности к начальным условиям. Малейшее воздействие, от которого невозможно избавиться – округление переменной (если это теоретическая модель), ошибка измерения (если это исследование реальной системы) – и система ведет себя совершенно по-другому.
Лоренц приводил наглядный пример: если погода действительно относится к классу настолько чувствительных систем (разумеется, не все системы такие), то взмах крыльев чайки может вызвать заметные изменения погоды. Впоследствии чайка была заменена бабочкой, а в 1972 году появилась работа «Предсказуемость: может ли взмах крыльев бабочки в Бразилии вызвать торнадо в Техасе?».
Так родился знаменитый термин «эффект бабочки», отсылавший и к рассказу Брэдбери и, удивительным образом, к следующему открытию Лоренца – странному аттрактору, названному в его честь.
Неожиданная структура
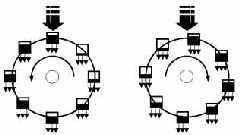
Лоренц построил похожую, но более простую модель из трех уравнений с тремя переменными. Модель описывала конвекцию в газе и жидкости, а также поведение несложного механического устройства – водяного колеса Лоренца (см. иллюстрацию). Под напором воды, наполняющей емкости (и вытекающей из них сквозь небольшие отверстия), колесо ведет себя удивительно сложным образом: замедляет вращение, ускоряет его, начинает вращаться в другую сторону, останавливается – в общем, как и положено уважающей себя хаотической системе.
Водяное колесо Лоренца. Изображение с сайта ast.cam.ac.uk. Кликните на картинку, чтобы увидеть ее целиком.
Для наглядного отображения поведения системы Лоренц использовал не обычный временной график, а фазовый портрет. Три числа, описывающие состояние системы, обозначали координаты точки в трехмерном пространстве. С каждым шагом на фазовом портрете появлялась новая точка.
Если бы система рано или поздно приходила к полной устойчивости, добавление точек рано или поздно должно было полностью остановиться. Если бы она приходила к периодическим колебаниям, линия из точек образовала бы кольцо. Наконец, если в поведении системы не было бы вообще никаких закономерностей, на фазовом портрете могло бы появиться что угодно.
Результат оказался совершенно неожиданным. Объект, который появился на портрете (см. главную иллюстрацию), располагался в определенных границах, не пересекая их. Он обладал определенной структурой – напоминал два крыла бабочки – но в ее пределах был совершенно неупорядочен. Он не прекращал «развиваться»: ни одна новая точка не совпадала с предыдущей, фазовый портрет можно было строить бесконечно. Переход от одного из крыльев к другому соответствовал началу вращения колеса в другую сторону.
Такие объекты – странные аттракторы – сыграли большую роль во фрактальной геометрии и теории хаоса. «Крылья бабочки» получили название «аттрактор Лоренца».
Теория хаоса
Второй шок – в этом хаосе, оказывается, спрятан порядок. Неожиданный, странный, плохо понятный, представляющий собой «тонкую структуру, таящуюся в беспорядочном потоке информации» (Дж. Глейк), но тем более интересный. Аттрактор Лоренца не решает проблемы предсказания, но уже само его существование достойно изучения.
Поисками подобных проявлений порядка в хаосе и занимается сравнительно молодая наука – теория хаоса. Она возникла не мгновенно и не имеет одного создателя. Ее основы были заложены в работах Пуанкаре, Колмогорова, Арнольда, Ляпунова, Ландау, Смэйла, Мандельброта, Фейгенбаума и десятков других талантливых ученых, либо увидевших то, что до них никто не видел, либо сумевших описать то, что увидели другие.
Одним же из ключевых моментов (далеко не сразу, кстати, оцененным по достоинству) в ее возникновении считается день, когда Эдвард Нортон Лоренц, любитель погоды и упорный искатель странного, ввел в свою модель значения переменных, округленные до трех знаков после запятой.